5.1相交线-2020-2021学年人教版七年级数学下册专题复习提升训练试卷(Word版含答案)
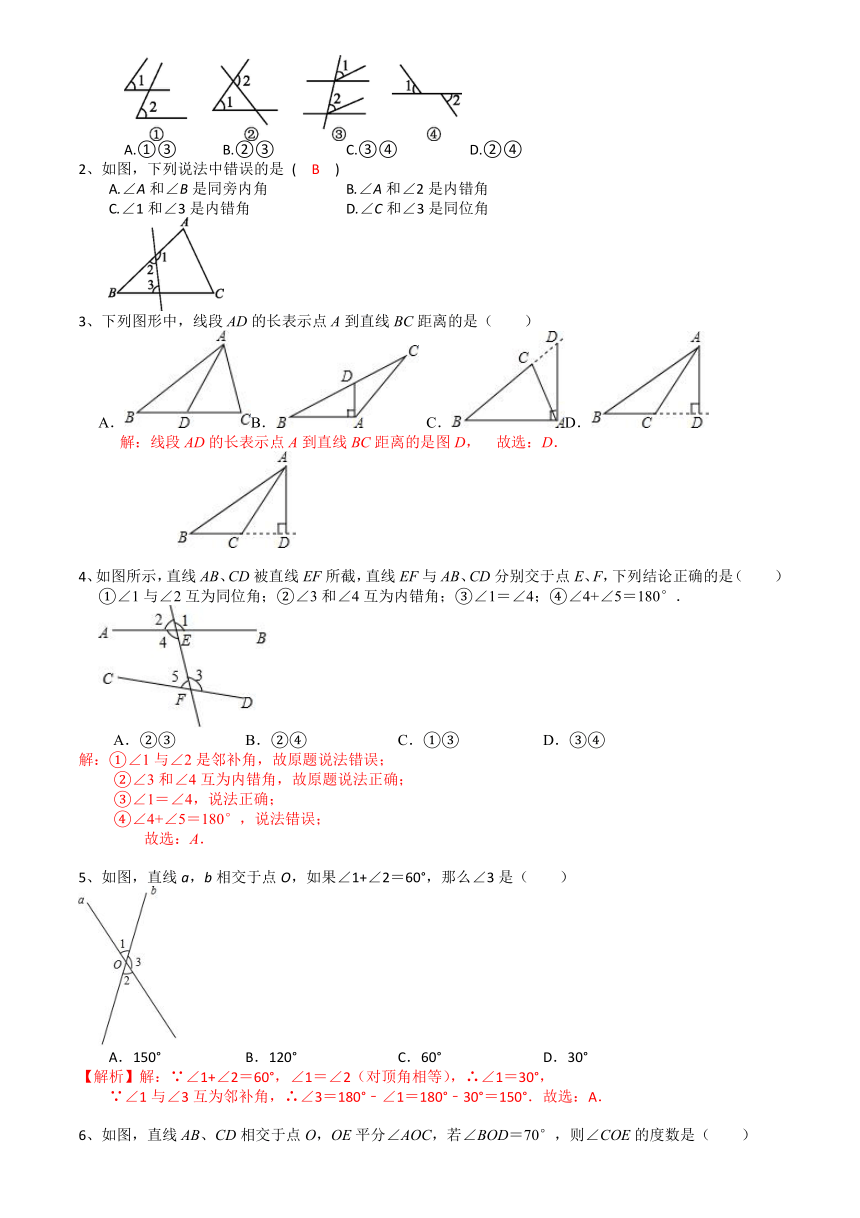
文档属性
| 名称 | 5.1相交线-2020-2021学年人教版七年级数学下册专题复习提升训练试卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 483.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 00:00:00 | ||
图片预览

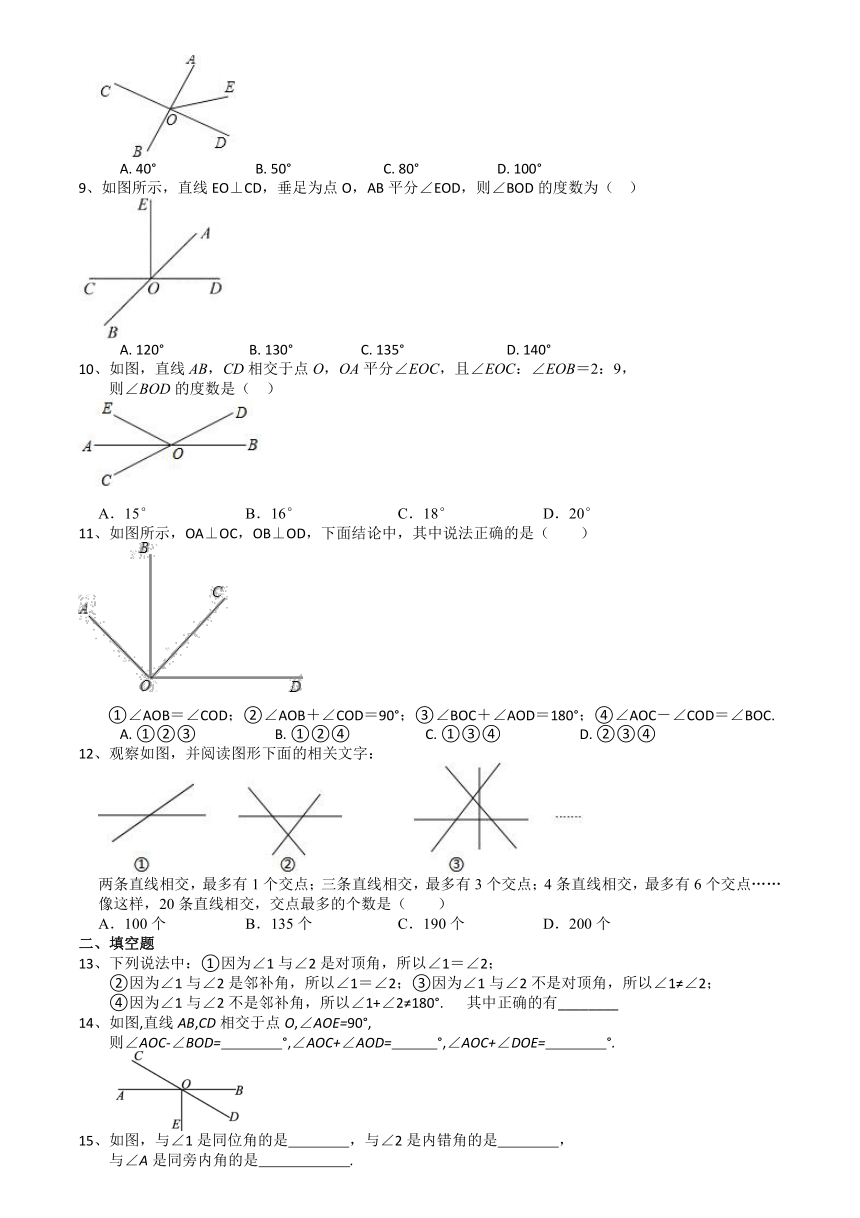
文档简介
专题复习提升训练卷5.1相交线-20-21人教版七年级数学下册
一、选择题
1、如图,∠1与∠2是同位角的是 ( )
A.①③ B.②③ C.③④ D.②④
2、如图,下列说法中错误的是 ( )
A.∠A和∠B是同旁内角 B.∠A和∠2是内错角 C.∠1和∠3是内错角 D.∠C和∠3是同位角
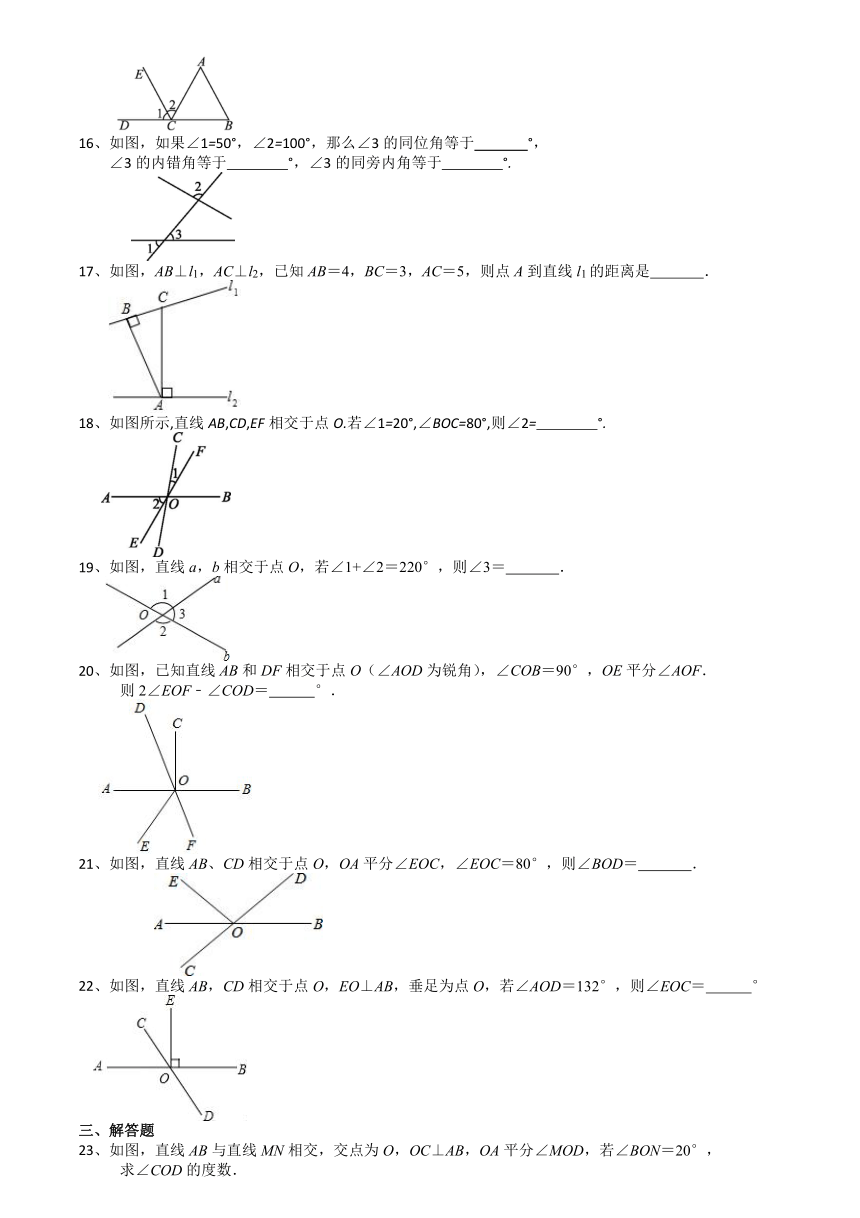
3、下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.B. C.D.
4、如图所示,直线AB、CD被直线EF所截,直线EF与AB、CD分别交于点E、F,下列结论正确的是( )
①∠1与∠2互为同位角;②∠3和∠4互为内错角;③∠1=∠4;④∠4+∠5=180°.
A.②③ B.②④ C.①③ D.③④
5、如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150° B.120° C.60° D.30°
6、如图,直线AB、CD相交于点O,OE平分∠AOC,若∠BOD=70°,则∠COE的度数是( )
A.70° B.50° C.40° D.35°
7、如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,
则∠3的度数为 ( )
A.40° B.50° C.60° D.70°
8、如图,直线AB、CD相交于点O,OE平分∠AOD,若∠BOC=80°,则∠AOE的度数是( )
A.?40°????????????????????????????B.?50°??????????????????????????C.?80°??????????????????????D.?100°
9、如图所示,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为(?? )
A.?120°????????????????????????B.?130°???????????????????C.?135°?????????????????????????????D.?140°
10、如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOB=2:9,
则∠BOD的度数是( )
A.15° B.16° C.18° D.20°
11、如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.?①②③??????????????????????B.?①②④?????????????????????C.?①③④??????????????????????D.?②③④
12、观察如图,并阅读图形下面的相关文字:
两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;4条直线相交,最多有6个交点……
像这样,20条直线相交,交点最多的个数是( )
A.100个 B.135个 C.190个 D.200个
二、填空题
13、下列说法中:①因为∠1与∠2是对顶角,所以∠1=∠2;
②因为∠1与∠2是邻补角,所以∠1=∠2;③因为∠1与∠2不是对顶角,所以∠1≠∠2;
④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°. 其中正确的有________
14、如图,直线AB,CD相交于点O,∠AOE=90°,
则∠AOC-∠BOD= °,∠AOC+∠AOD= °,∠AOC+∠DOE= °.?
15、如图,与∠1是同位角的是 ,与∠2是内错角的是 ,
与∠A是同旁内角的是 .?
16、如图,如果∠1=50°,∠2=100°,那么∠3的同位角等于 °,
∠3的内错角等于 °,∠3的同旁内角等于 °.?
17、如图,AB⊥l1,AC⊥l2,已知AB=4,BC=3,AC=5,则点A到直线l1的距离是 .
18、如图所示,直线AB,CD,EF相交于点O.若∠1=20°,∠BOC=80°,则∠2= °.?
19、如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3= .
20、如图,已知直线AB和DF相交于点O(∠AOD为锐角),∠COB=90°,OE平分∠AOF.
则2∠EOF﹣∠COD= °.
21、如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=80°,则∠BOD= .
22、如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= °
三、解答题
23、如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,
求∠COD的度数.
24、如图,直线AB,CD相交于点O,OE平分∠AOC,∠EOA∶∠AOD=1∶4,求∠EOB的度数.
25、如图,三条直线AB、CD、EF共点于O,三个交角的关系是∠3=3∠2、∠2=2∠1,
求∠1、∠2、∠3的大小.
26、如图,直线AB,CD相交于点O,OE平分∠AOD.
(1)若∠AOC=46°,求∠BOE的度数;
(2)若∠AOC=x°,求∠BOE的度数.
27、如图,直线AB、CD相交于点O,OE平分∠BOD
(1)若∠AOC=60°,求∠BOE的度数;
(2)若OF平分∠AOD,试说明OE⊥OF.
28、已知,直线AB与直线CD相交于点O,OB平分∠DOF.
(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(0<x<90),
求∠AOE的度数.(用含x的代数式表示)
专题复习提升训练卷5.1相交线-20-21人教版七年级数学下册(答案)
一、选择题
1、如图,∠1与∠2是同位角的是 ( B )
A.①③ B.②③ C.③④ D.②④
2、如图,下列说法中错误的是 ( B )
A.∠A和∠B是同旁内角 B.∠A和∠2是内错角
C.∠1和∠3是内错角 D.∠C和∠3是同位角
3、下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.B. C.D.
解:线段AD的长表示点A到直线BC距离的是图D, 故选:D.
4、如图所示,直线AB、CD被直线EF所截,直线EF与AB、CD分别交于点E、F,下列结论正确的是( )
①∠1与∠2互为同位角;②∠3和∠4互为内错角;③∠1=∠4;④∠4+∠5=180°.
A.②③ B.②④ C.①③ D.③④
解:①∠1与∠2是邻补角,故原题说法错误;
②∠3和∠4互为内错角,故原题说法正确;
③∠1=∠4,说法正确;
④∠4+∠5=180°,说法错误;
故选:A.
5、如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150° B.120° C.60° D.30°
【解析】解:∵∠1+∠2=60°,∠1=∠2(对顶角相等),∴∠1=30°,
∵∠1与∠3互为邻补角,∴∠3=180°﹣∠1=180°﹣30°=150°.故选:A.
6、如图,直线AB、CD相交于点O,OE平分∠AOC,若∠BOD=70°,则∠COE的度数是( )
A.70° B.50° C.40° D.35°
解:∵∠BOD=70°,∴∠AOC=∠BOD=70°,
∵OE平分∠AOC,∴∠COE=∠AOC=×70°=35°,故选:D.
7、如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,
则∠3的度数为 ( )
A.40° B.50° C.60° D.70°
[解析] 因为∠1=∠2,∠1+∠2=80°,所以∠1=∠2=40°,所以∠BOC=140°.因为OE平分∠BOC,所以∠3=70°.
故选D.
8、如图,直线AB、CD相交于点O,OE平分∠AOD,若∠BOC=80°,则∠AOE的度数是( A )
A.?40°????????????????????????????B.?50°??????????????????????????C.?80°??????????????????????D.?100°
9、如图所示,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为(C?? )
A.?120°????????????????????????B.?130°???????????????????C.?135°?????????????????????????????D.?140°
10、如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOB=2:9,
则∠BOD的度数是(C )
A.15° B.16° C.18° D.20°
11、如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( C )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.?①②③??????????????????????B.?①②④?????????????????????C.?①③④??????????????????????D.?②③④
12、观察如图,并阅读图形下面的相关文字:
两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;4条直线相交,最多有6个交点……
像这样,20条直线相交,交点最多的个数是( )
A.100个 B.135个 C.190个 D.200个
解:2条直线相交最多有1个交点,1=×1×2,
3条直线相交最多有3个交点,3=1+2=×2×3,
4条直线相交最多有6个交点,6=1+2+3=×3×4,
5条直线相交最多有10个交点,10=1+2+3+4=×4×5,
…
n条直线相交最多有交点的个数是:n(n﹣1).
20条直线相交最多有交点的个数是:n(n﹣1)=×20×19=190.
故选:C.
二、填空题
13、下列说法中:①因为∠1与∠2是对顶角,所以∠1=∠2;
②因为∠1与∠2是邻补角,所以∠1=∠2;③因为∠1与∠2不是对顶角,所以∠1≠∠2;
④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°. 其中正确的有____①____
14、如图,直线AB,CD相交于点O,∠AOE=90°,
则∠AOC-∠BOD= °,∠AOC+∠AOD= °,∠AOC+∠DOE= °.?
【答案】0 180 90
15、如图,与∠1是同位角的是 ,与∠2是内错角的是 ,
与∠A是同旁内角的是 .?
【答案】∠B ∠A ∠ACB,∠B
16、如图,如果∠1=50°,∠2=100°,那么∠3的同位角等于 °,
∠3的内错角等于 °,∠3的同旁内角等于 °.?
【答案】80 80 100
17、如图,AB⊥l1,AC⊥l2,已知AB=4,BC=3,AC=5,则点A到直线l1的距离是 .
解:∵AB⊥l1,
则点A到直线l1的距离是AB的长=4; 故答案为:4.
18、如图所示,直线AB,CD,EF相交于点O.若∠1=20°,∠BOC=80°,则∠2= 60 °.?
19、如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3= .
解:∵∠1=∠2,∠1+∠2=220°,∴∠1=∠2=110°,∴∠3=180°﹣110°=70°,
故答案为:70°.
20、如图,已知直线AB和DF相交于点O(∠AOD为锐角),∠COB=90°,OE平分∠AOF.
则2∠EOF﹣∠COD= 90 °.
21、如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=80°,则∠BOD= 40° .
22、如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= °.
【解答】解:∵∠AOD=132°,∴∠COB=132°,
∵EO⊥AB,∴∠EOB=90°,∴∠COE=132°﹣90°=42°,
故答案为:42.
三、解答题
23、如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,
求∠COD的度数.
【解答】解:∵∠BON=20°,∴∠AOM=20°,
∵OA平分∠MOD,∴∠AOD=∠MOA=20°,
∵OC⊥AB,∴∠AOC=90°,∴∠COD=90°﹣20°=70°.
24、如图,直线AB,CD相交于点O,OE平分∠AOC,∠EOA∶∠AOD=1∶4,求∠EOB的度数.
解:设∠EOA=x.∵OE平分∠AOC,∴∠AOC=2x.
∵∠EOA∶∠AOD=1∶4,∴∠AOD=4x.
∵∠AOC+∠AOD=180°, ∴2x+4x=180°,解得x=30°,
∴∠EOB=180°-30°=150°. 故∠EOB的度数是150°.
25、如图,三条直线AB、CD、EF共点于O,三个交角的关系是∠3=3∠2、∠2=2∠1,
求∠1、∠2、∠3的大小.
解:设∠1=x°,那么∠2=2∠1=2x°,∠3=3∠2=6x°;
∵∠2=∠FOD,∠1+∠FOD+∠3=180°,
∴x+2x+6x=180,解得,x=20,
即:∠1=20°,∠2=40°,∠3=120°,
26、如图,直线AB,CD相交于点O,OE平分∠AOD.
(1)若∠AOC=46°,求∠BOE的度数;
(2)若∠AOC=x°,求∠BOE的度数.
解:(1)∵∠AOC=46°, ∴∠AOD=180°-∠AOC=180°-46°=134°.
∵OE平分∠AOD,∴∠DOE=∠AOD=×134°=67°.
∵∠BOD=∠AOC=46°, ∴∠BOE=∠DOE+∠BOD=67°+46°=113°.
(2)∵∠AOC=x°, ∴∠AOD=180°-∠AOC=(180-x)°.
∵OE平分∠AOD,∴∠DOE=∠AOD=(180-x)°=90-x°.
∵∠BOD=∠AOC=x°,∴∠BOE=∠DOE+∠BOD=90-x°+x°=°.
27、如图,直线AB、CD相交于点O,OE平分∠BOD
(1)若∠AOC=60°,求∠BOE的度数;
(2)若OF平分∠AOD,试说明OE⊥OF.
【解答】解:(1)∵直线AB、CD相交于点O,∴∠BOD=∠AOC=60°,
又∵OE平分∠BOD,∴∠BOE=∠BOD=30°;
(2)∵OF平分∠AOD,∴∠DOF=∠AOD,
又∵OE平分∠BOD,∴∠DOE=∠BOD,
∴∠EOF=∠DOF+∠DOE=(∠AOD+∠BOD)=×180°=90°. ∴OE⊥OF.
28、已知,直线AB与直线CD相交于点O,OB平分∠DOF.
(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(0<x<90),
求∠AOE的度数.(用含x的代数式表示)
解:(1)∵OB平分∠DOF,∴∠BOD=∠BOF=40°,∴∠AOC=40°;
(2)∵OB平分∠DOF,∴∠BOD=∠BOF,
∵∠BOF=x°,∴∠BOD=x°,∴∠AOC=∠BOD=x°,
如图1,∵∠COE=60°,∴∠AOE=∠AOC+∠COE=(60+x)°(0<x<90);
如图2,当0<x≤60时,∵∠COE=60°,∴∠AOE=∠COE﹣∠AOC=(60﹣x)°(0<x≤60),
当60<x<90时,如图3中,∵∠COE=60°,
∴∠AOE=∠AOC+∠COE=(x+60)°(60<x<90),
或∠AOE′=∠AOC﹣∠COE′=(x﹣60)°
综上所述:∠AOE的度数为(60+x)°或|60﹣x|°.
一、选择题
1、如图,∠1与∠2是同位角的是 ( )
A.①③ B.②③ C.③④ D.②④
2、如图,下列说法中错误的是 ( )
A.∠A和∠B是同旁内角 B.∠A和∠2是内错角 C.∠1和∠3是内错角 D.∠C和∠3是同位角
3、下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.B. C.D.
4、如图所示,直线AB、CD被直线EF所截,直线EF与AB、CD分别交于点E、F,下列结论正确的是( )
①∠1与∠2互为同位角;②∠3和∠4互为内错角;③∠1=∠4;④∠4+∠5=180°.
A.②③ B.②④ C.①③ D.③④
5、如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150° B.120° C.60° D.30°
6、如图,直线AB、CD相交于点O,OE平分∠AOC,若∠BOD=70°,则∠COE的度数是( )
A.70° B.50° C.40° D.35°
7、如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,
则∠3的度数为 ( )
A.40° B.50° C.60° D.70°
8、如图,直线AB、CD相交于点O,OE平分∠AOD,若∠BOC=80°,则∠AOE的度数是( )
A.?40°????????????????????????????B.?50°??????????????????????????C.?80°??????????????????????D.?100°
9、如图所示,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为(?? )
A.?120°????????????????????????B.?130°???????????????????C.?135°?????????????????????????????D.?140°
10、如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOB=2:9,
则∠BOD的度数是( )
A.15° B.16° C.18° D.20°
11、如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.?①②③??????????????????????B.?①②④?????????????????????C.?①③④??????????????????????D.?②③④
12、观察如图,并阅读图形下面的相关文字:
两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;4条直线相交,最多有6个交点……
像这样,20条直线相交,交点最多的个数是( )
A.100个 B.135个 C.190个 D.200个
二、填空题
13、下列说法中:①因为∠1与∠2是对顶角,所以∠1=∠2;
②因为∠1与∠2是邻补角,所以∠1=∠2;③因为∠1与∠2不是对顶角,所以∠1≠∠2;
④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°. 其中正确的有________
14、如图,直线AB,CD相交于点O,∠AOE=90°,
则∠AOC-∠BOD= °,∠AOC+∠AOD= °,∠AOC+∠DOE= °.?
15、如图,与∠1是同位角的是 ,与∠2是内错角的是 ,
与∠A是同旁内角的是 .?
16、如图,如果∠1=50°,∠2=100°,那么∠3的同位角等于 °,
∠3的内错角等于 °,∠3的同旁内角等于 °.?
17、如图,AB⊥l1,AC⊥l2,已知AB=4,BC=3,AC=5,则点A到直线l1的距离是 .
18、如图所示,直线AB,CD,EF相交于点O.若∠1=20°,∠BOC=80°,则∠2= °.?
19、如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3= .
20、如图,已知直线AB和DF相交于点O(∠AOD为锐角),∠COB=90°,OE平分∠AOF.
则2∠EOF﹣∠COD= °.
21、如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=80°,则∠BOD= .
22、如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= °
三、解答题
23、如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,
求∠COD的度数.
24、如图,直线AB,CD相交于点O,OE平分∠AOC,∠EOA∶∠AOD=1∶4,求∠EOB的度数.
25、如图,三条直线AB、CD、EF共点于O,三个交角的关系是∠3=3∠2、∠2=2∠1,
求∠1、∠2、∠3的大小.
26、如图,直线AB,CD相交于点O,OE平分∠AOD.
(1)若∠AOC=46°,求∠BOE的度数;
(2)若∠AOC=x°,求∠BOE的度数.
27、如图,直线AB、CD相交于点O,OE平分∠BOD
(1)若∠AOC=60°,求∠BOE的度数;
(2)若OF平分∠AOD,试说明OE⊥OF.
28、已知,直线AB与直线CD相交于点O,OB平分∠DOF.
(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(0<x<90),
求∠AOE的度数.(用含x的代数式表示)
专题复习提升训练卷5.1相交线-20-21人教版七年级数学下册(答案)
一、选择题
1、如图,∠1与∠2是同位角的是 ( B )
A.①③ B.②③ C.③④ D.②④
2、如图,下列说法中错误的是 ( B )
A.∠A和∠B是同旁内角 B.∠A和∠2是内错角
C.∠1和∠3是内错角 D.∠C和∠3是同位角
3、下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.B. C.D.
解:线段AD的长表示点A到直线BC距离的是图D, 故选:D.
4、如图所示,直线AB、CD被直线EF所截,直线EF与AB、CD分别交于点E、F,下列结论正确的是( )
①∠1与∠2互为同位角;②∠3和∠4互为内错角;③∠1=∠4;④∠4+∠5=180°.
A.②③ B.②④ C.①③ D.③④
解:①∠1与∠2是邻补角,故原题说法错误;
②∠3和∠4互为内错角,故原题说法正确;
③∠1=∠4,说法正确;
④∠4+∠5=180°,说法错误;
故选:A.
5、如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3是( )
A.150° B.120° C.60° D.30°
【解析】解:∵∠1+∠2=60°,∠1=∠2(对顶角相等),∴∠1=30°,
∵∠1与∠3互为邻补角,∴∠3=180°﹣∠1=180°﹣30°=150°.故选:A.
6、如图,直线AB、CD相交于点O,OE平分∠AOC,若∠BOD=70°,则∠COE的度数是( )
A.70° B.50° C.40° D.35°
解:∵∠BOD=70°,∴∠AOC=∠BOD=70°,
∵OE平分∠AOC,∴∠COE=∠AOC=×70°=35°,故选:D.
7、如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,
则∠3的度数为 ( )
A.40° B.50° C.60° D.70°
[解析] 因为∠1=∠2,∠1+∠2=80°,所以∠1=∠2=40°,所以∠BOC=140°.因为OE平分∠BOC,所以∠3=70°.
故选D.
8、如图,直线AB、CD相交于点O,OE平分∠AOD,若∠BOC=80°,则∠AOE的度数是( A )
A.?40°????????????????????????????B.?50°??????????????????????????C.?80°??????????????????????D.?100°
9、如图所示,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为(C?? )
A.?120°????????????????????????B.?130°???????????????????C.?135°?????????????????????????????D.?140°
10、如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOB=2:9,
则∠BOD的度数是(C )
A.15° B.16° C.18° D.20°
11、如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( C )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.?①②③??????????????????????B.?①②④?????????????????????C.?①③④??????????????????????D.?②③④
12、观察如图,并阅读图形下面的相关文字:
两条直线相交,最多有1个交点;三条直线相交,最多有3个交点;4条直线相交,最多有6个交点……
像这样,20条直线相交,交点最多的个数是( )
A.100个 B.135个 C.190个 D.200个
解:2条直线相交最多有1个交点,1=×1×2,
3条直线相交最多有3个交点,3=1+2=×2×3,
4条直线相交最多有6个交点,6=1+2+3=×3×4,
5条直线相交最多有10个交点,10=1+2+3+4=×4×5,
…
n条直线相交最多有交点的个数是:n(n﹣1).
20条直线相交最多有交点的个数是:n(n﹣1)=×20×19=190.
故选:C.
二、填空题
13、下列说法中:①因为∠1与∠2是对顶角,所以∠1=∠2;
②因为∠1与∠2是邻补角,所以∠1=∠2;③因为∠1与∠2不是对顶角,所以∠1≠∠2;
④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°. 其中正确的有____①____
14、如图,直线AB,CD相交于点O,∠AOE=90°,
则∠AOC-∠BOD= °,∠AOC+∠AOD= °,∠AOC+∠DOE= °.?
【答案】0 180 90
15、如图,与∠1是同位角的是 ,与∠2是内错角的是 ,
与∠A是同旁内角的是 .?
【答案】∠B ∠A ∠ACB,∠B
16、如图,如果∠1=50°,∠2=100°,那么∠3的同位角等于 °,
∠3的内错角等于 °,∠3的同旁内角等于 °.?
【答案】80 80 100
17、如图,AB⊥l1,AC⊥l2,已知AB=4,BC=3,AC=5,则点A到直线l1的距离是 .
解:∵AB⊥l1,
则点A到直线l1的距离是AB的长=4; 故答案为:4.
18、如图所示,直线AB,CD,EF相交于点O.若∠1=20°,∠BOC=80°,则∠2= 60 °.?
19、如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3= .
解:∵∠1=∠2,∠1+∠2=220°,∴∠1=∠2=110°,∴∠3=180°﹣110°=70°,
故答案为:70°.
20、如图,已知直线AB和DF相交于点O(∠AOD为锐角),∠COB=90°,OE平分∠AOF.
则2∠EOF﹣∠COD= 90 °.
21、如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=80°,则∠BOD= 40° .
22、如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC= °.
【解答】解:∵∠AOD=132°,∴∠COB=132°,
∵EO⊥AB,∴∠EOB=90°,∴∠COE=132°﹣90°=42°,
故答案为:42.
三、解答题
23、如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=20°,
求∠COD的度数.
【解答】解:∵∠BON=20°,∴∠AOM=20°,
∵OA平分∠MOD,∴∠AOD=∠MOA=20°,
∵OC⊥AB,∴∠AOC=90°,∴∠COD=90°﹣20°=70°.
24、如图,直线AB,CD相交于点O,OE平分∠AOC,∠EOA∶∠AOD=1∶4,求∠EOB的度数.
解:设∠EOA=x.∵OE平分∠AOC,∴∠AOC=2x.
∵∠EOA∶∠AOD=1∶4,∴∠AOD=4x.
∵∠AOC+∠AOD=180°, ∴2x+4x=180°,解得x=30°,
∴∠EOB=180°-30°=150°. 故∠EOB的度数是150°.
25、如图,三条直线AB、CD、EF共点于O,三个交角的关系是∠3=3∠2、∠2=2∠1,
求∠1、∠2、∠3的大小.
解:设∠1=x°,那么∠2=2∠1=2x°,∠3=3∠2=6x°;
∵∠2=∠FOD,∠1+∠FOD+∠3=180°,
∴x+2x+6x=180,解得,x=20,
即:∠1=20°,∠2=40°,∠3=120°,
26、如图,直线AB,CD相交于点O,OE平分∠AOD.
(1)若∠AOC=46°,求∠BOE的度数;
(2)若∠AOC=x°,求∠BOE的度数.
解:(1)∵∠AOC=46°, ∴∠AOD=180°-∠AOC=180°-46°=134°.
∵OE平分∠AOD,∴∠DOE=∠AOD=×134°=67°.
∵∠BOD=∠AOC=46°, ∴∠BOE=∠DOE+∠BOD=67°+46°=113°.
(2)∵∠AOC=x°, ∴∠AOD=180°-∠AOC=(180-x)°.
∵OE平分∠AOD,∴∠DOE=∠AOD=(180-x)°=90-x°.
∵∠BOD=∠AOC=x°,∴∠BOE=∠DOE+∠BOD=90-x°+x°=°.
27、如图,直线AB、CD相交于点O,OE平分∠BOD
(1)若∠AOC=60°,求∠BOE的度数;
(2)若OF平分∠AOD,试说明OE⊥OF.
【解答】解:(1)∵直线AB、CD相交于点O,∴∠BOD=∠AOC=60°,
又∵OE平分∠BOD,∴∠BOE=∠BOD=30°;
(2)∵OF平分∠AOD,∴∠DOF=∠AOD,
又∵OE平分∠BOD,∴∠DOE=∠BOD,
∴∠EOF=∠DOF+∠DOE=(∠AOD+∠BOD)=×180°=90°. ∴OE⊥OF.
28、已知,直线AB与直线CD相交于点O,OB平分∠DOF.
(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(0<x<90),
求∠AOE的度数.(用含x的代数式表示)
解:(1)∵OB平分∠DOF,∴∠BOD=∠BOF=40°,∴∠AOC=40°;
(2)∵OB平分∠DOF,∴∠BOD=∠BOF,
∵∠BOF=x°,∴∠BOD=x°,∴∠AOC=∠BOD=x°,
如图1,∵∠COE=60°,∴∠AOE=∠AOC+∠COE=(60+x)°(0<x<90);
如图2,当0<x≤60时,∵∠COE=60°,∴∠AOE=∠COE﹣∠AOC=(60﹣x)°(0<x≤60),
当60<x<90时,如图3中,∵∠COE=60°,
∴∠AOE=∠AOC+∠COE=(x+60)°(60<x<90),
或∠AOE′=∠AOC﹣∠COE′=(x﹣60)°
综上所述:∠AOE的度数为(60+x)°或|60﹣x|°.
