期末复习 必刷经典题-2020-2021学年苏科版八年级数学下册(含答案)
文档属性
| 名称 | 期末复习 必刷经典题-2020-2021学年苏科版八年级数学下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 869.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 07:17:56 | ||
图片预览

文档简介
期末复习必刷23经典例题
数学思想方法:
整体思想,数形结合思想,分类讨论思想,化归的思想
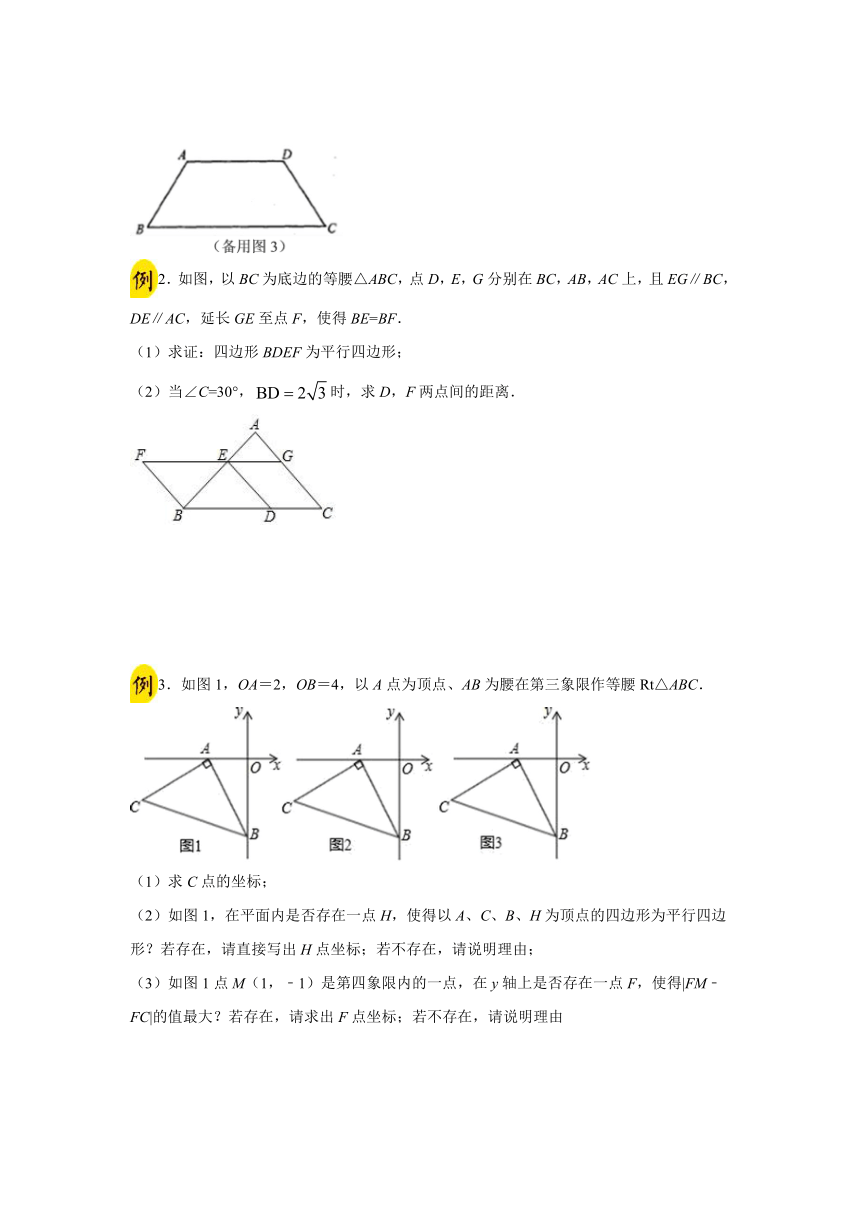
1.如图,在等腰梯形ABCD中,false,false,false,false.点Р从点B出发沿折线段false以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点O向上作射线OKIBC,交折线段falsefalse于点E.点P、O同时开始运动,为点Р与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒false.
(1)点P到达终点C时,求t的值,并指出此时BQ的长;
(2)当点Р运动到AD上时,t为何值能使false?
(3)t为何值时,四点P、Q、C、E成为一个平行四边形的顶点?
(4)false能为直角三角形时t的取值范围________.(直接写出结果)
(注:备用图不够用可以另外画)
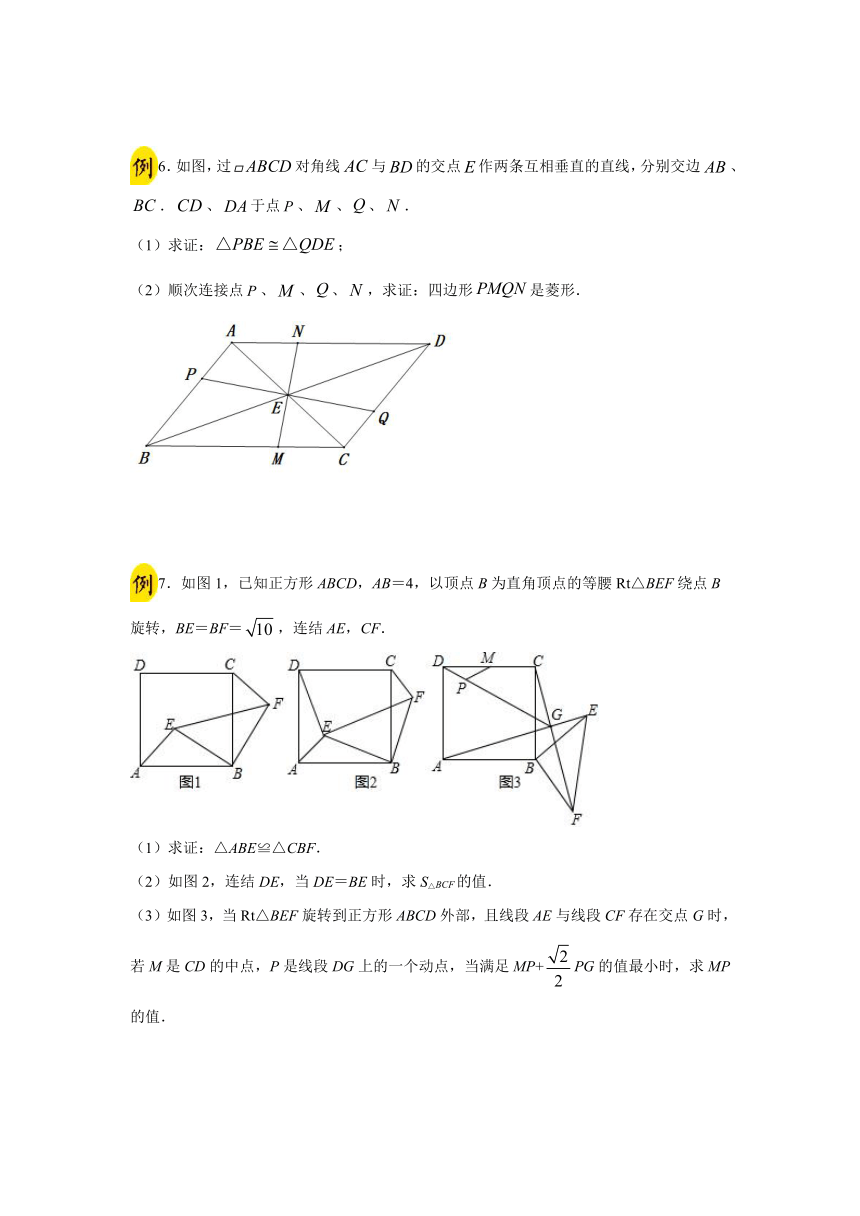
2.如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=30°,false时,求D,F两点间的距离.
3.如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
(1)求C点的坐标;
(2)如图1,在平面内是否存在一点H,使得以A、C、B、H为顶点的四边形为平行四边形?若存在,请直接写出H点坐标;若不存在,请说明理由;
(3)如图1点M(1,﹣1)是第四象限内的一点,在y轴上是否存在一点F,使得|FM﹣FC|的值最大?若存在,请求出F点坐标;若不存在,请说明理由
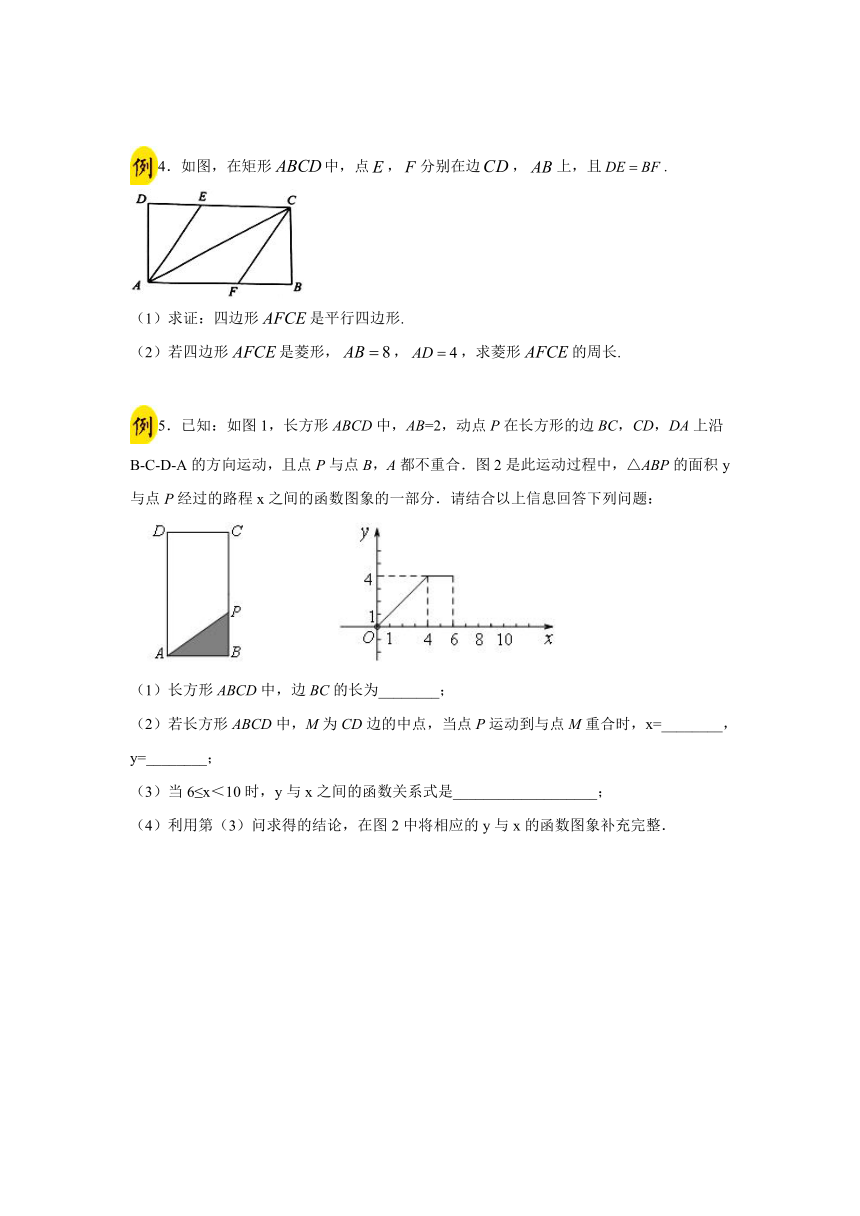
4.如图,在矩形false中,点false,false分别在边false,false上,且false.
(1)求证:四边形false是平行四边形.
(2)若四边形false是菱形,false,false,求菱形false的周长.
5.已知:如图1,长方形ABCD中,AB=2,动点P在长方形的边BC,CD,DA上沿B-C-D-A的方向运动,且点P与点B,A都不重合.图2是此运动过程中,△ABP的面积y与点P经过的路程x之间的函数图象的一部分.请结合以上信息回答下列问题:
(1)长方形ABCD中,边BC的长为________;
(2)若长方形ABCD中,M为CD边的中点,当点P运动到与点M重合时,x=________,y=________;
(3)当6≤x<10时,y与x之间的函数关系式是___________________;
(4)利用第(3)问求得的结论,在图2中将相应的y与x的函数图象补充完整.
6.如图,过false对角线false与false的交点false作两条互相垂直的直线,分别交边false、false.false、false于点false、false、false、false.
(1)求证:false;
(2)顺次连接点false、false、false、false,求证:四边形false是菱形.
7.如图1,已知正方形ABCD,AB=4,以顶点B为直角顶点的等腰Rt△BEF绕点B旋转,BE=BF=false,连结AE,CF.
(1)求证:△ABE≌△CBF.
(2)如图2,连结DE,当DE=BE时,求S△BCF的值.
(3)如图3,当Rt△BEF旋转到正方形ABCD外部,且线段AE与线段CF存在交点G时,若M是CD的中点,P是线段DG上的一个动点,当满足MP+falsePG的值最小时,求MP的值.
8.计算:false
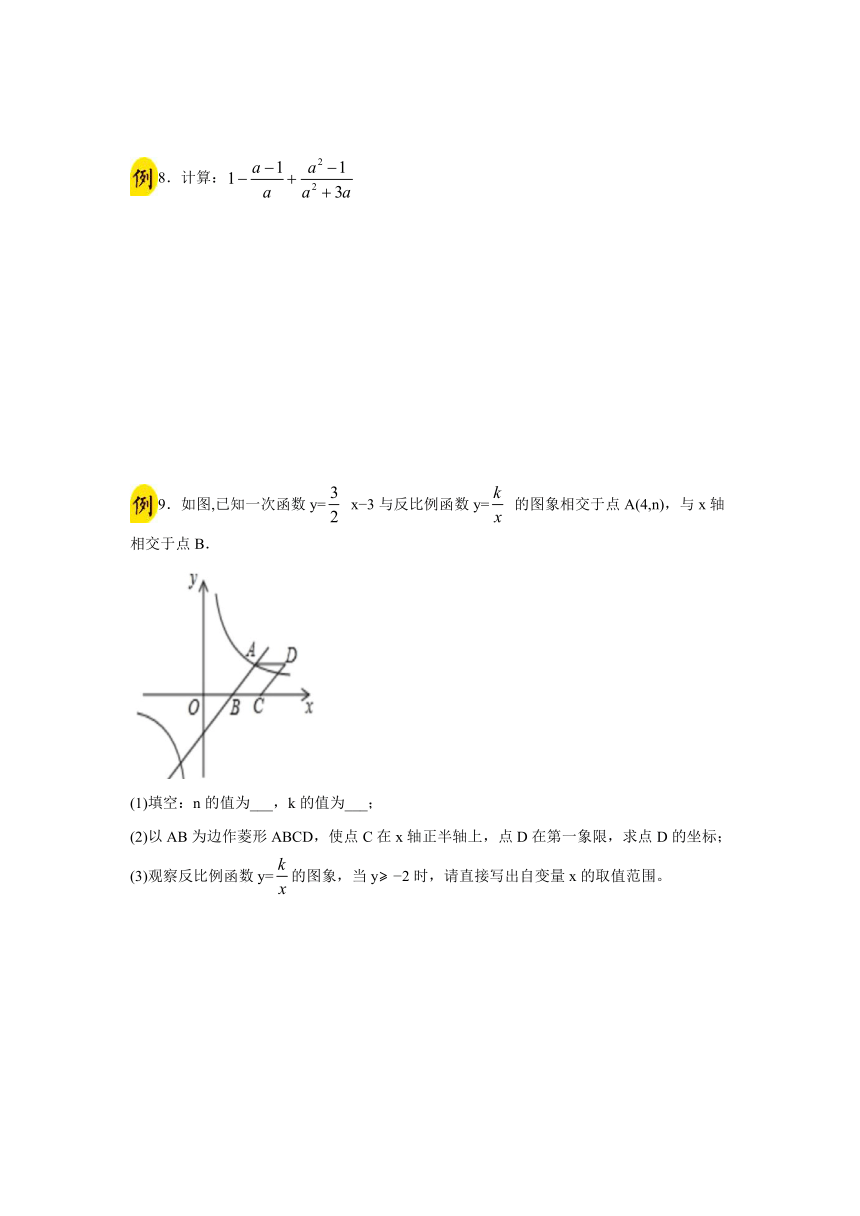
9.如图,已知一次函数y=false x?3与反比例函数y=false 的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为___,k的值为___;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y=false的图象,当y??2时,请直接写出自变量x的取值范围。
10.已知:如图,一次函数y=kx+3的图象与反比例函数y=false (x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C.点D,且S△DBP=27,false
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式
11.先化简,再求值:false,其中false.
12.false.
13.false
14.如图,一个圆形转盘被平均分成8个小扇形.请在这8个小扇形中分别写上数字1、2、3,任意转动转盘,使得转盘停止转动后,“指针落在数字1的区域”的可能性最大,且“指针落在数字2的区域”的可能性与“指针落在数字3的区域”的可能性相同.
15.先化简false,然后从-2,-1, 0, 1中选取一个你认为合适的数作为x的值代入求值.
16.解方程false.
17.△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点O顺时针旋转90°得到△A2B2C2,
(2)按照(1)中②作图,回答下列问题:△A2B2C2中顶点A2坐标为 ,B2的坐标为 ,若P(a,b)为△ABC边上一点,则点P对应的点Q的坐标为 .
18.如图所示的正方形网格中,△ABC的顶点均在格点上,请按要求画图:
(1)以点A为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于点O成中心对称的△A2B2C2.
19.如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足﹣(a﹣4)2≥0,c=false+8.
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求false的值.
20.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数false
100
150
200
500
800
1000
摸到白球的次数false
59
96
false
295
480
601
摸到白球的频率false
false
0.64
0.58
0.59
0.60
0.601
(1)上表中的false________,false________;
(2)“摸到白球的”的概率的估计值是_________(精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
21.在一个不透明的盒子中装有a个除颜色外完全相同的红球和白球,其中红球有b个,将盒中的球摇匀后从中任意摸出1个球,记录颜色后将球放回盒中,重复进行这过程,如表记录了某班一次摸球实验情况:
摸球总数n
400
1500
3500
7000
9000
14000
摸到红球数m
325
1336
3203
6335
8073
12628
摸到红球的频率(精确到0.001)
0.813
0.891
0.915
0.905
0.897
0.902
(1)由此估计任意摸出1个球为红球的概率约是 (精确到0.1)
(2)实验结束后,小明发现了一个一般性的结论:盒子中共有a个球,其中红球有b个,则摇匀后从中任意摸出1个球为红球的概率P可以表示为false,这个结论也得到了老师的证实根据小明的发现,若在该盒子中再放入除颜色外与原来的球完全相同的2个红球和2个白球,摇匀后从中任意摸出1个球为红球的概率为P’,请通过计算比较P与P'的大小.
22.如图1,像false这样,由false和false组合成的封闭图形,我们称之为K型GHMNQ.在平面直角坐标系中,false,false,点C,D,E分别在线段AB,AO,BO上运动,且ADCEB为K型.
(1)如图2,若点D运动到点O时,过点O作false,交CE的延长线为F,连接BF,求证:false;
(2)如图3,若C是AB的中点,当false为等腰三角形时,请直接写出AD的长.
23.某中学开展了“实施素质教育,快乐课余生活”的活动,该校根据实际情况,决定主要开设false:体育,false:音乐,false:美术,false:科技制作这四个课外活动小组,活动实施前,该校为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下的不完整的条形统计图和扇形统计图,请你结合图中信息解答下列问题:
(1)样本中最喜欢false项目的人数的百分比是________,其所在扇形统计图中的圆心角的度数是________;
(2)把条形统计图补充完整;
(3)已知该校有false人,根据样本估计全校最喜欢体育的人数。
常考热点反思:
常考热点反思:
答案
1.(1) false秒,false;(2)解析:考查线的平行问题;(3)false;(4)false或false.
2.(1)解析:考查平行四边形的证明;(2)false.
3.(1)(﹣6,﹣2)
4.(1)解析:考查平行四边形的证明;(2)20.
5.(1)4;(2)5,4;(3)y=10?x;
6.(1)解析:考查三角形全等的证明;(2)解析:考查平行四边形的证明
7.(1)解析:考查三角形全等的证明;(2)6;(3)false
8.原式=false
9.(1)n=3,k=12;(2)(4+false,3);(3)x??6或x>0.
10.(1)(0,3);(2)y=?falsex+3,y=?false
11.1
12.false
13.false
14.解析:作图,考虑轴对称,旋转性质
15.false,-false.
16.x=-1.
17.(2)(4,2),(2,4),(b,﹣a).
18.解析:作图,考虑轴对称,旋转性质
19.(1)y=2x+8,D(2,2);(2)存在,5;(3)false.
20.(1)false,false.(2)0.6. (3)8个.
21.(1)0.9;(2)P>P'
22.(2)3或6或false
23.(1)20% ;72°;(3)880人
数学思想方法:
整体思想,数形结合思想,分类讨论思想,化归的思想
1.如图,在等腰梯形ABCD中,false,false,false,false.点Р从点B出发沿折线段false以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点O向上作射线OKIBC,交折线段falsefalse于点E.点P、O同时开始运动,为点Р与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒false.
(1)点P到达终点C时,求t的值,并指出此时BQ的长;
(2)当点Р运动到AD上时,t为何值能使false?
(3)t为何值时,四点P、Q、C、E成为一个平行四边形的顶点?
(4)false能为直角三角形时t的取值范围________.(直接写出结果)
(注:备用图不够用可以另外画)
2.如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=30°,false时,求D,F两点间的距离.
3.如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
(1)求C点的坐标;
(2)如图1,在平面内是否存在一点H,使得以A、C、B、H为顶点的四边形为平行四边形?若存在,请直接写出H点坐标;若不存在,请说明理由;
(3)如图1点M(1,﹣1)是第四象限内的一点,在y轴上是否存在一点F,使得|FM﹣FC|的值最大?若存在,请求出F点坐标;若不存在,请说明理由
4.如图,在矩形false中,点false,false分别在边false,false上,且false.
(1)求证:四边形false是平行四边形.
(2)若四边形false是菱形,false,false,求菱形false的周长.
5.已知:如图1,长方形ABCD中,AB=2,动点P在长方形的边BC,CD,DA上沿B-C-D-A的方向运动,且点P与点B,A都不重合.图2是此运动过程中,△ABP的面积y与点P经过的路程x之间的函数图象的一部分.请结合以上信息回答下列问题:
(1)长方形ABCD中,边BC的长为________;
(2)若长方形ABCD中,M为CD边的中点,当点P运动到与点M重合时,x=________,y=________;
(3)当6≤x<10时,y与x之间的函数关系式是___________________;
(4)利用第(3)问求得的结论,在图2中将相应的y与x的函数图象补充完整.
6.如图,过false对角线false与false的交点false作两条互相垂直的直线,分别交边false、false.false、false于点false、false、false、false.
(1)求证:false;
(2)顺次连接点false、false、false、false,求证:四边形false是菱形.
7.如图1,已知正方形ABCD,AB=4,以顶点B为直角顶点的等腰Rt△BEF绕点B旋转,BE=BF=false,连结AE,CF.
(1)求证:△ABE≌△CBF.
(2)如图2,连结DE,当DE=BE时,求S△BCF的值.
(3)如图3,当Rt△BEF旋转到正方形ABCD外部,且线段AE与线段CF存在交点G时,若M是CD的中点,P是线段DG上的一个动点,当满足MP+falsePG的值最小时,求MP的值.
8.计算:false
9.如图,已知一次函数y=false x?3与反比例函数y=false 的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为___,k的值为___;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y=false的图象,当y??2时,请直接写出自变量x的取值范围。
10.已知:如图,一次函数y=kx+3的图象与反比例函数y=false (x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C.点D,且S△DBP=27,false
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式
11.先化简,再求值:false,其中false.
12.false.
13.false
14.如图,一个圆形转盘被平均分成8个小扇形.请在这8个小扇形中分别写上数字1、2、3,任意转动转盘,使得转盘停止转动后,“指针落在数字1的区域”的可能性最大,且“指针落在数字2的区域”的可能性与“指针落在数字3的区域”的可能性相同.
15.先化简false,然后从-2,-1, 0, 1中选取一个你认为合适的数作为x的值代入求值.
16.解方程false.
17.△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点O顺时针旋转90°得到△A2B2C2,
(2)按照(1)中②作图,回答下列问题:△A2B2C2中顶点A2坐标为 ,B2的坐标为 ,若P(a,b)为△ABC边上一点,则点P对应的点Q的坐标为 .
18.如图所示的正方形网格中,△ABC的顶点均在格点上,请按要求画图:
(1)以点A为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于点O成中心对称的△A2B2C2.
19.如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足﹣(a﹣4)2≥0,c=false+8.
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求false的值.
20.在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数false
100
150
200
500
800
1000
摸到白球的次数false
59
96
false
295
480
601
摸到白球的频率false
false
0.64
0.58
0.59
0.60
0.601
(1)上表中的false________,false________;
(2)“摸到白球的”的概率的估计值是_________(精确到0.1);
(3)如果袋中有12个白球,那么袋中除了白球外,还有多少个其它颜色的球?
21.在一个不透明的盒子中装有a个除颜色外完全相同的红球和白球,其中红球有b个,将盒中的球摇匀后从中任意摸出1个球,记录颜色后将球放回盒中,重复进行这过程,如表记录了某班一次摸球实验情况:
摸球总数n
400
1500
3500
7000
9000
14000
摸到红球数m
325
1336
3203
6335
8073
12628
摸到红球的频率(精确到0.001)
0.813
0.891
0.915
0.905
0.897
0.902
(1)由此估计任意摸出1个球为红球的概率约是 (精确到0.1)
(2)实验结束后,小明发现了一个一般性的结论:盒子中共有a个球,其中红球有b个,则摇匀后从中任意摸出1个球为红球的概率P可以表示为false,这个结论也得到了老师的证实根据小明的发现,若在该盒子中再放入除颜色外与原来的球完全相同的2个红球和2个白球,摇匀后从中任意摸出1个球为红球的概率为P’,请通过计算比较P与P'的大小.
22.如图1,像false这样,由false和false组合成的封闭图形,我们称之为K型GHMNQ.在平面直角坐标系中,false,false,点C,D,E分别在线段AB,AO,BO上运动,且ADCEB为K型.
(1)如图2,若点D运动到点O时,过点O作false,交CE的延长线为F,连接BF,求证:false;
(2)如图3,若C是AB的中点,当false为等腰三角形时,请直接写出AD的长.
23.某中学开展了“实施素质教育,快乐课余生活”的活动,该校根据实际情况,决定主要开设false:体育,false:音乐,false:美术,false:科技制作这四个课外活动小组,活动实施前,该校为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下的不完整的条形统计图和扇形统计图,请你结合图中信息解答下列问题:
(1)样本中最喜欢false项目的人数的百分比是________,其所在扇形统计图中的圆心角的度数是________;
(2)把条形统计图补充完整;
(3)已知该校有false人,根据样本估计全校最喜欢体育的人数。
常考热点反思:
常考热点反思:
答案
1.(1) false秒,false;(2)解析:考查线的平行问题;(3)false;(4)false或false.
2.(1)解析:考查平行四边形的证明;(2)false.
3.(1)(﹣6,﹣2)
4.(1)解析:考查平行四边形的证明;(2)20.
5.(1)4;(2)5,4;(3)y=10?x;
6.(1)解析:考查三角形全等的证明;(2)解析:考查平行四边形的证明
7.(1)解析:考查三角形全等的证明;(2)6;(3)false
8.原式=false
9.(1)n=3,k=12;(2)(4+false,3);(3)x??6或x>0.
10.(1)(0,3);(2)y=?falsex+3,y=?false
11.1
12.false
13.false
14.解析:作图,考虑轴对称,旋转性质
15.false,-false.
16.x=-1.
17.(2)(4,2),(2,4),(b,﹣a).
18.解析:作图,考虑轴对称,旋转性质
19.(1)y=2x+8,D(2,2);(2)存在,5;(3)false.
20.(1)false,false.(2)0.6. (3)8个.
21.(1)0.9;(2)P>P'
22.(2)3或6或false
23.(1)20% ;72°;(3)880人
同课章节目录
