2020-2021学年北师大版数学六下第三单元《图形的运动》期中章节复习精编讲义(含解析)
文档属性
| 名称 | 2020-2021学年北师大版数学六下第三单元《图形的运动》期中章节复习精编讲义(含解析) | 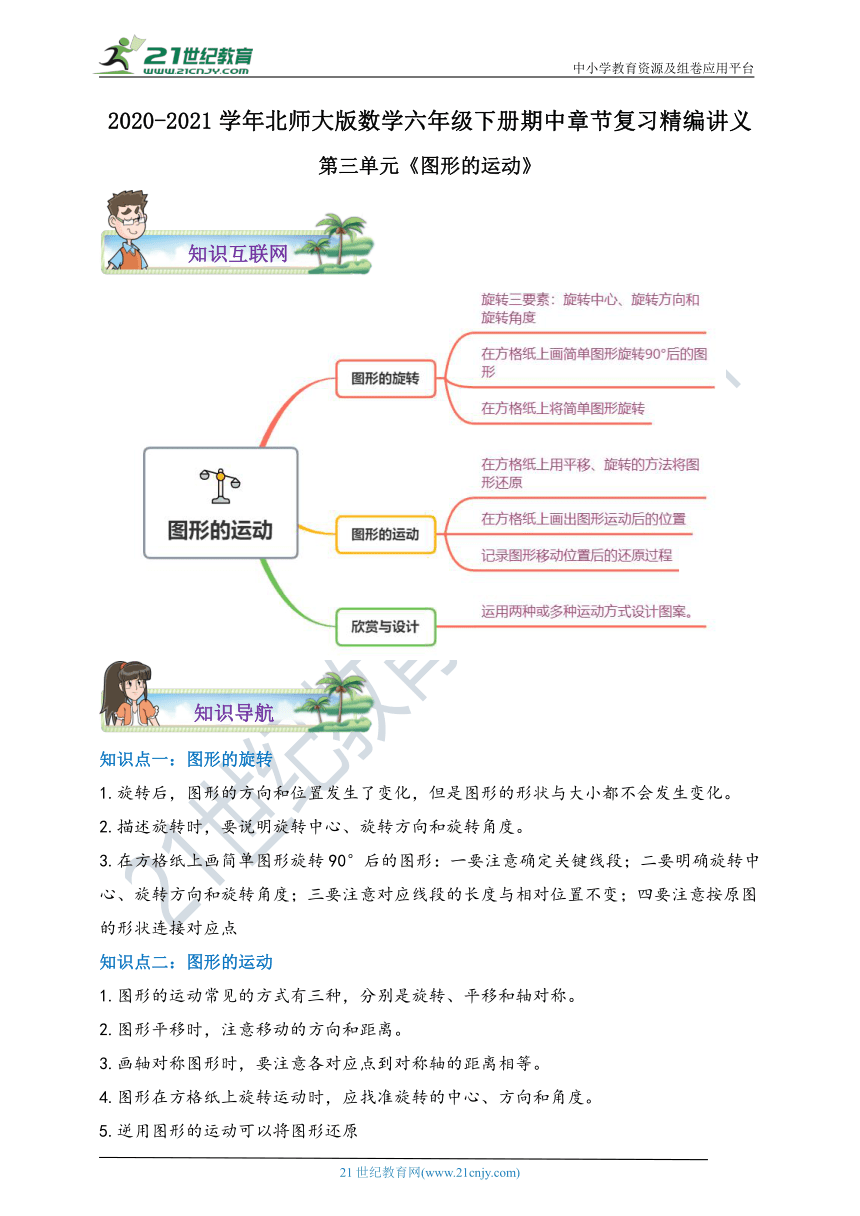 | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 09:10:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年北师大版数学六年级下册期中章节复习精编讲义
第三单元《图形的运动》
知识点一:图形的旋转
1.旋转后,图形的方向和位置发生了变化,但是图形的形状与大小都不会发生变化。
2.描述旋转时,要说明旋转中心、旋转方向和旋转角度。
3.在方格纸上画简单图形旋转90°后的图形:一要注意确定关键线段;二要明确旋转中心、旋转方向和旋转角度;三要注意对应线段的长度与相对位置不变;四要注意按原图的形状连接对应点
知识点二:图形的运动
1.图形的运动常见的方式有三种,分别是旋转、平移和轴对称。
2.图形平移时,注意移动的方向和距离。
3.画轴对称图形时,要注意各对应点到对称轴的距离相等。
4.图形在方格纸上旋转运动时,应找准旋转的中心、方向和角度。
5.逆用图形的运动可以将图形还原
知识点三:欣赏与设计
1.欣赏美丽的图案,要注意分析图案的构造,注意找出其中的基本图形,明确基本图形经过怎样的运动才能形成这幅图案。
2.可以单独利用图形的某一种运动方式设计图案,也可以综合运用两种或多种运动方式设计图案。
3.利用图形的变换方式设计图案时,首先要选好基本图形,然后确定运动方式,最后画出变换后的图案
一、精挑细选(共5题;每题1分,共5分)
1.
如图,三角形ABC怎样旋转可以得到三角形A'BC'?下面说法正确的是(???
)
A.?绕B点逆时针旋转90°??????????????????????????????????????????B.?绕B点顺时针旋转90°
C.?绕C点顺时针旋转90°??????????????????????????????????????????D.?绕C点逆时针旋转180°
2.
以点C为中心旋转的图形是(???
)。
A.????????????B.????????????C.?
3.
如图,点A的位置用数对表示是(1,5)。线段OA绕点O按顺时针方向旋转90°,点A的对应点A’的位置用数对表示是(??
)。
A.?(5,5)???????????????????????????B.?(5,1)???????????????????????????C.?(4,1)???????????????????????????D.?(6,1)
4.
将图形
A(?
),可以得到图形B.
A.?向右平移3格,再绕O点逆时针旋转90°
B.?向右平移5格,再绕O点顺时针旋转90°
C.?向右平移3格,再绕O点顺时针旋转90°
5.
如图中,图形A变换到图形B,下列描述不正确的是(?
)
A.?图形A先向右平移4格,再向下平移2格,然后以直径所在的直线作轴对称图形得到图形B
B.?图形A先向下平移2格,再向右平移4格,然后以直径所在的直线作轴对称图形得到图形B
C.?图形A先以直径所在的直线作轴对称图形,再向下平移4格,再向右平移2格,得到图形B
D.?图形A先以直径所在的直线作轴对称图形,再向右平移4格,再向下平移2格,得到图形B
二、判断正误(共5题;每题1分,共5分)
6.
如图,图1先顺时针旋转90°,再向右平移6个格,就可以得到图2。(???
)
7.
一个图形顺时针旋转180°和逆时针旋转180°,所得到的两个图形正好重合。
8.
旋转中,对应点划过的痕迹是一条圆弧。
9.
每个旋转的图形都有一个旋转中心或一个旋转轴。
10.
图形旋转后所对应的一组线段的夹角是90°,说明这个图形旋转了90°。(
??)
三、仔细想,认真填(共10题;每空1分,共36分)
11.
(
5分
)
如图所示,图形A到图形B向________平移了________格,图形B绕点O________时针旋转________得到图形C,图形C还可以看作是图形B的________.
12.
如图,A点的位置是(7,8),B点的位置是(10,3),将三角形AOB绕点O逆时针旋转90°到一个新的三角形A'OB',那么,A点的对应点A'的位置是(________,
________),B点的对应点B'的位置是(________,________)
13.
如图,
图形①绕点O逆时针旋转90°,得到图形________;图形③绕点o逆时针旋转90°得到图形________。
14.
下图每个小正方形的边长表示1厘米。
(1)在正方形方格纸上有一个三角形ABC,请用数对表示出C点的位置________。
(2)这个三角形的面积是________平方厘米。
(3)画出这个三角形绕C点顺时针旋转90度,再向右平移8格后的图形。
15.
正方形绕对称轴的交点至少旋转________度后与原图形重合;长方形绕对称轴的交点至少旋转________度后与原图形重合。
16.
在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为________,这个定点称为________,转动的角为________。
17.
下面图形绕O点顺时针旋转90°后的图形是________,顺时针旋转180°的图形是________
18.
下图中的指针从C开始,顺时针旋转180°指向________,指针从D开始,逆时针旋转90°指向________。
A.点A?????????????
B.
点B?????
???????C
.点C???????????
D
.点D
19.
如图
(1)以直线MN为________作图形A的________,得到图形B。
(2)将图形B绕点O________旋转________,得到图形C。
(3)将图形C向________平移________格,得到图形D。
20.
按要求在方格纸上画图(每个小方格表示1平方厘米)
(1)先用数对表示图中A点位置是________,再画出把图中的三角形绕A点顺时针旋转90?后得到的图形。在旋转过程中,B点划过的路程有________厘米。
(2)按1:2画出圆缩小后的图形,缩小后的图形面积是原来的________。
四、解答问题(共5题;共30.5分)
21.
(
6.5分
)
操作实践,动手动脑。
(1)画出三角形AOB关于直线MN对称的图形。
(2)若B点的位置可以用(x,y)表示,则A点的位置为________。
(3)画出三角形AOB绕点A逆时针旋转90°后的图形。
22.
(
8分
)
(1)用数对表示C点的位置(________,________).
(2)将小旗图围绕A点顺时针旋转90°
(3)将平行四边形向上平移4格,再向右平移5格。
(4)将三角形按2:1的比放大。
23.
(
3分
)
下图中,图形A是如何变换得到图形B?
24.
(
6分
)
(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形。旋转后,B点的位置用数对表示是(??
,??
).
(2)按1:2的比画出三角形缩小后的图形。缩小后的三角形的面积是原来的
。
(3)如果1个小方格表示1平方厘米,在方格纸上设计一个面积是8平方厘米的轴对称图形,并画出它的一条对称轴。
25.
(
7分
)
按要求完成下面各题。
(1)把图中的长方形绕点A顺时针旋转90°,画出旋转后的图形。点B旋转后的对应点B’的位置用数对表示是_________。
(2)按1:2的比例画出三角形缩小后的图形。缩小后的三角形的面积是原来的
________。
(3)如果1个小方格表示1cm2
,
在方格纸上设计一个面积是8cm2的轴对称图形,并画出它的一条对称轴。
五、巧妙作图(共2题;共15分)
26.
(
6分
)
(1)以直线l为对称轴画出图形①的对称图形②。
(2)先将图形②向右平移4格,再以点O为中心逆时针旋转90?,得到图形③,画出图形③。
27.
(
9分
)
在方格纸上按要求完成作业。
(1)将图A向左平移5格。
(2)将图B按点O顺时针方向旋转90o。
(3)以直线L为对称轴,画出已知图形C的轴对称图形。
六、综合提升(共2题;共8.5分)
28.
(
4分
)
小动物们分别向哪个方向平移?平移几格才能吃到它们喜欢的食物?
(1)小兔先向________平移________格,再向________平移________格,吃到胡萝卜。
(2)小狗先向________平移________格,再向________平移________格,吃到骨头。
29.
(
4.5分
)
观察图形,填写空格。
(1)①号图形绕A点按________时针方向旋转了________°;
(2)②号图形绕________点按顺时针方向旋转了________°;
(3)③号图形绕________点按________时针方向旋转了90";
(4)④号图形绕________点按________时针方向旋转了________°。
一、精挑细选
1.B
解:B点没变,说明是绕B点旋转的;观察线段AB和A'B',线段AB顺时针旋转90°是A'B',所以
三角形ABC绕B点顺时针旋转90°
得到三角形A'BC'。
故答案为:B。
思路引导:旋转是图形绕某定点沿某方向移动。特点:大小、形状不变、方向和位置变化。一条线段的旋转和整个图形的旋转是一样的。
2.B
以点C为中心旋转的图形是B。
故答案为:B。
思路引导:绕点C旋转则,则旋转后的图形与原图形的点C重合。
3.B
解:如图
A′的位置用数对表示是(5,1)。
故答案为:B。
思路引导:先确定旋转中心,然后根据旋转方向和度数画出旋转后的图形,然后用数对表示A′,数对中第一个数表示列,第二个数表示行。
4.C
解:根据题干分析可得:图形A先向右平移3格,再绕点O顺时针旋转90度,即可得出图形B,
故选:C.
思路引导:观察图形,根据图形旋转和平移的方法可得:图形A先向右平移3格,再绕点O顺时针旋转90度,即可得出图形B,据此即可选择.此题考查了利用旋转和平移进行图形变换的方法的灵活应用.
5.C
解:如图,
图形A变换到图形B,下列描述不正确的是:
A、图形A先向右平移4格,再向下平移2格,然后以直径所在的直线作轴对称图形得到图形B,正确;
B、图形A先向下平移2格,再向右平移4格,然后以直径所在的直线作轴对称图形得到图形B,正确;
C、图形A先以直径所在的直线作轴对称图形,再向下平移4格,再向右平移2格,得到图形B;不正确;
D、图形A先以直径所在的直线作轴对称图形,再向右平移4格,再向下平移2格,得到图形B,正确.
故选:C.
思路引导:根据平移的特征和轴对称图形的特征,图形A先向右平移4格,再向下平移2格,然后以直径所在的直线作轴对称图形得到图形B;或图形A先向下平移2格,再向右平移4格;或图形A先以直径所在的直线作轴对称图形,再向下平移2格,再向右平移4格,得到图形B;图形A先以直径所在的直线作轴对称图形,再向右平移4格,再向下平移2格,得到图形B,此题主查考查平移、轴对称的特征.平移作图要注意:①方向;②距离.整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动.此题的错误所右就是没弄清平移的距离;求作一个几何图形关于某条直线对称的图形,可以转化为求作这个图形上的特征点关于这条直线对称的点,然后依次连结各对称点即可.
二、判断正误
6.错误
如图,图1先逆时针旋转90°,再向右平移6个格,就可以得到图2,原题说法错误.
故答案为:错误.
思路引导:此题主要考查图形的旋转和平移,图形的旋转,弄清旋转中心、旋转的方向和角度,观察可知,以笑脸上的一点A为旋转中心,笑脸绕点A逆时针旋转了90°;平移时,要注意平移的方向和格数,观察图中笑脸的对应点是向右平移了6格,那么这个图形就向右平移了6格,据此判断.
7.正确
解:一个图形按某一个固定点顺时针旋转180度和逆时针旋转180度,所得到的两个图形正好重合,原题说法正确.
故答案为:正确
思路引导:顺时针和逆时针旋转180°,图形都是正好颠倒位置,只是运动的方向不同,所得到的图形是重合的.
8.正确
解:旋转中,对应点划过的痕迹是一条圆弧,原题说法正确.
故答案为:正确
思路引导:旋转中,对应的点划过的痕迹是一条圆弧,圆弧的圆心角就是旋转的度数.
9.正确
解:根据旋转图形的定义可知,每个旋转的图形都有一个旋转中心或一个旋转轴,原题说法正确.
故答案为:正确
思路引导:旋转是围绕着一个点或轴运动的,这个点就是旋转中心,这条轴就是旋转轴,由此判断即可.
10.正确
解:图形旋转后所对应的一组线段的夹角是90°,说明这个图形旋转了90°。原题说法正确。
故答案为:正确。
思路引导:旋转的度数就是旋转前后两个图形对应的线段之间的夹角,由此判断即可。
三、仔细想,认真填
11.右;4;顺;90°;轴对称图形
解:图形A到图形B向右平移了4格,图形B绕点O顺时针旋转90°得到图形C,图形C还可以看作图形B的轴对称图形。
故答案为:右;4;顺;90°;轴对称图形。
思路引导:平移,是指在平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。平移不改变图形的形状和大小。根
旋转:在平面内,把一个图形绕点O旋转一个角度的图形变换叫做旋转,点O叫做旋转中心,旋转的角叫做旋转角,如果图形上的点P经过旋转变为点Pˊ,那么这两个点叫做这个旋转的对应点。
轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。
12.2;3;7;6
解:如图:
A′的位置是(2,3),B′的位置是(7,6)。
故答案为:2,3;7,6。
思路引导:根据旋转中心、方向和度数画出旋转后的图形,然后根据两点所在的列与行用数对表示即可。
13.④;②
解:图形①绕点O逆时针旋转90°,得到图形④;图形③绕点O逆时针旋转90°得到图形②。
故答案为:④;②。
思路引导:旋转中心是O点,然后确定旋转方向,因为是旋转90°,所以对应边的夹角是直角,由此确定旋转后得到的图形即可。
14.(1)(3,4)(2)3
(1)C的位置是(3,4).
(2)三角形的面积:
2×3×
=6×
=3(平方厘米).
(3)根据分析,作图如下:
.
故答案为:(1)(3,4);(2)3;(3)
思路引导:(1)用数对表示位置时,第一个数字表示第几列,第二个数字表示第几行,中间用“,”隔开,据此解答;
(2)观察图可知,三角形的底是2厘米,高是3厘米,求三角形的面积,用公式:三角形的面积=底×高×
,
据此列式解答;
(3)画旋转图形的方法:按照旋转要求的方向,以这条线段为一条边,以旋转中心为顶点,画出旋转要求角度的角;在画出的这条射线上截取与已知线段相等长度的线段即为所求,据此画出旋转后的图形;然后向右平移8格,画出图形即可.
15.90;180
解:正方形绕对称轴的交点至少旋转90度后与原图形重合;长方形绕对称轴的交点至少旋转180度后与原图形重合。
故答案为:90;180。
思路引导:旋转时正方形一个顶点到相邻的另一个顶点时,就能与原图形重合;长方形的一个顶点到相对的顶点时才能与原图形重合。
16.旋转;旋转中心;旋转角
解:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角为旋转角.
故答案为:旋转;旋转中心;旋转角
思路引导:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角为旋转角.要掌握旋转三要素:旋转中心、旋转方向、旋转度数.
17.D;B
解:图形绕A点顺时针旋转90°后的图形开口向下,是图形D;
顺时针旋转180°开口向左,是图形B.
故答案为:D,B
思路引导:先确定旋转中心,再确定旋转方向和度数,注意抓住图形的主要特征来确定旋转后的图形.
18.B;C
解:指针从C开始,顺时针旋转180°成一条直线,指针指向B点;指针从D开始,逆时针旋转90°,和C点成直角,指向C点.
故答案为:B,C
思路引导:先确定旋转中心,再根据旋转方向和度数确定指针的指向;注意与钟面上指针转动的方向相同的是顺时针,与指针转动方向相反的是逆时针.
19.(1)对称轴;轴对称图形
(2)顺时针;90°
(3)右;六
解:(1)以直线MN对称轴作图形A的轴对称图形,得到图形B;
(2)将图形B绕点O顺时针旋转90°,得到图形C;
(3)将图形C像右平移六格,得到图形D.
故答案为:(1)对称轴;轴对称图形;(2)顺时针;90°;(3)右;六
思路引导:(1)图形A和B是以直线MN为轴对称的;(2)根据BC的位置确定旋转的方向和度数即可;(3)根据CD的位置确定平移的方向和格数即可.
20.(1)(4,7);12.56
(2)
(1)
先用数对表示图中A点位置是(4,7),再画出把图中的三角形绕A点顺时针旋转90?后得到的图形。在旋转过程中,B点划过的路程有2×4×3.14×=6.28厘米,作图如下:
;
(2)
按1:2画出圆缩小后的图形,缩小后的图形面积是原来的
,
作图如下:
.
故答案为:(1)(4,7);12.56;(2).
思路引导:(1)用数对表示位置时,第一个数字表示第几列,第二个数字表示第几行,中间用逗号隔开,据此表示出A点的位置;
要求画出图中的三角形绕A点顺时针旋转90?后得到的图形,弄清旋转中心、旋转的方向和角度,按照旋转要求的方向,以这条线段为一条边,以旋转中心为顶点,画出旋转要求角度的角;在画出的这条射线上截取与已知线段相等长度的线段即为所求,按原图连接各点即可;
观察可知,在旋转过程中,B点划过的痕迹是半径为4厘米的圆的弧长,先求出圆的周长,再乘即可;
(2)观察图形可知,原来的圆的半径是2厘米,要求按1:2画出圆缩小后的图形,先确定缩小后圆的半径,缩小后的圆的半径是1厘米,据此作图,然后分别求出缩小后的面积和原来圆的面积,最后相除即可得到缩小了多少,据此解答.
四、解答问题
21.(1)解:如图所示:
(2)(x+3,y+2)
(3)解:如图所示:
思路引导:(1)画轴对称图形的方法:①点出关键点,找出所有的关键点,即图形中所有线段的端点;②确定关键点到对称轴的距离,关键点离对称轴多远,对称点就离对称轴多远;③点出对称点;④连线,按照给出的一半图形将所有对称点连接成线段。
(2)用数对表示位置,先表示列,后表示行;
A点的位置为
(列数+3,行数+2)。
(3)
旋转作图,把一个图形绕其上面一点逆时针旋转一定的度数,先把这个点连接的边逆时针旋转指定的度数,然后把剩下的边连接起来即。
22.(1)2;8
(2)解:图形如下:
(3)解:图形如下:
(4)解:图形如下:
思路引导:(1)用数对表示点的位置时,这个点在第几列,数对中的第一个数字就写几,这个点在第几行,数对中的第二个数字就写几;
(2)把一个图形绕其上面一点,顺时针旋转一定的度数,先把这个点连接的边顺时针旋转相同的度数,然后把剩下的边连接起来即可;
(3)做平移后的图形,先把这个图形的关键点平移,然后把每条边连接起来即可;
(4)把一个图形按2:1的比放大,就是把这个图形的每条边都扩大2倍。
23.解:将图形A先向右平移5个格,再顺时针旋绕O点转90°即可得到图形B。
思路引导:观察两个图形的特征,需要进行一次平移,1次旋转才能得到图形B
,由此根据图形的特征描述变换方法即可。
24.(1)解:绕点A顺时针旋转90°得到图形1,如下图所示:
此时点B的位置为(7,6)。
(2)解:三角形按1:2的比例缩小后得到图形2,如下图所示:
三角形的面积=底×高÷2,底与高都缩小到原来的
,
则面积缩小到原来的×=。
(3)解:如图,图形3的面积是8平方厘米,它是一个长方形,它的对称轴有2条,分别是对边中点所在的直线。
思路引导:(1)画旋转图形的方法:把图形的每个点与旋转中心连接,再量出题目要求旋转的角度,最后依次连接;
用数对表示位置的方法是:第一个数字表示列,第二个数字表示行,中间用“,”隔开,据此解答;
(2)根据题意可知,先数一数原来直角三角形的两条直角边的格数,然后分别缩小到原来的
,
即可画出三角形缩小后的图形,三角形的面积=底×高÷2,当底和高都缩小到原来的
,
则缩小后的三角形的面积是原来的×=;
(3)根据题意可知,可以画一个长是4厘米,宽是2厘米的长方形,它的面积是8平方厘米,然后连接两条长的中点所在的直线就是它的一条对称轴,据此作图。
25.(1)图中蓝色的图形表示长方形旋转绕点A旋转90°后的图形,点B旋转后对应点B′的位置是(7,6)。
(2)假设每一个小正方形的边长为1,则大三角形的面积为:6×4÷2=12,缩小后三角形的面积为:3×2÷2=3,缩小后的三角形是原来的3÷12=。
答:缩小后的三角形如图形中的红色三角形。缩小后的三角形是原来的。
(3)轴对称图形有长方形、正方形、圆等等,以长方形为例,
面积是8cm2
则长方形长为4cm,宽为2cm,如图中的紫色图形,其中一条对称轴为长方形两条长边的中点的连线(如图中绿线)。
思路引导:(1)旋转:在平面内,把一个图形绕点O旋转一个角度的图形变换叫做旋转,点O叫做旋转中心,旋转的角叫做旋转角,如果图形上的点P经过旋转变为点Pˊ,那么这两个点叫做这个旋转的对应点。数对中的第一个数字表示列,第2个数字表示行,找出两个数字,中间用逗号隔开并用括号括起来;
(2)图形的缩小,即是按照比例将每一个边都缩小相同的倍数,原三角形的边长分别是6和4,缩小后三角形的边长分别是3和2,根据三角形的面积=底×高÷2,计算出原三角形和缩小后三角形的面积,再用缩小后的三角形面积除以原来三角形的面积即可得出答案;
(3)我们知道的轴对称图形有长方形、正方形、圆等等,以长方形为例,可得出面积为8cm2的长方形的长为4cm,宽为2cm,画出图形,找出它的对称轴即可。(沿对称轴折叠后图形两边完全重合)五、巧妙作图
26.(1)
(2)
思路引导:(1)画轴对称图形的方法是:数出或量出图形的关键点到对称轴的距离,在对称轴的另一侧找出关键点的对应点,按照所给图形的顺序连接各点;
(2)作平移图形的方法:先确定要平移图形的关键点,确定平移的方向是朝哪移的,然后确定移动的长度(格子数),最后把各点连接成图;
作旋转图形的方法:图形的旋转的关键是旋转中心、旋转方向和旋转的角度;画图时先弄清楚旋转的方向和角度,再确定从旋转点出发的两条线段旋转后的位置,这是关键所在,最后画其他的线段即可。
27.(1)
(2)
(3)
思路引导:(1)先确定平移的方向,然后根据平移的格数确定对应点的位置,再画出平移后的图形;
(2)先确定旋转中心,然后根据旋转方向和度数确定对应点的位置,然后画出旋转后的图形;
(3)轴对称图形对应点到对称轴的距离相等,先确定对应点的位置,再画出轴对称图形。
六、综合提升
28.(1)右;5;下;2
(2)上;4;左;3
解:(1)小兔先向右平移5格,再向下平移2格,吃到胡萝卜。
(2)小狗先向上平移4格,再向左平移3格,吃到骨头。
故答案为:(1)右;5;下;2;(2)上;4;左;3。(答案不唯一)
思路引导:平移,是指在平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。平移不改变图形的形状和大小。本题根据平移的特点进行解答。
29.(1)顺;90
(2)B;90
(3)C;逆
(4)D;顺;90
解:(1)①号图形绕A点按顺时针方向旋转了90°;
(2)②号图形绕B点按顺时针方向旋转了90°;
(3)③号图形绕C点按逆时针方向旋转了90°;
(4)④号图形绕D点按顺时针方向旋转了90°。
故答案为:(1)顺;90;(2)B;90;(3)C;逆;(4)D;顺;90。
思路引导:先确定旋转中心,然后判断旋转方向,根据对应边之间的夹角确定旋转度数即可。
知识互联网
知识导航
夯实基础
能力提升
能力达标百分训练(答案解析)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年北师大版数学六年级下册期中章节复习精编讲义
第三单元《图形的运动》
知识点一:图形的旋转
1.旋转后,图形的方向和位置发生了变化,但是图形的形状与大小都不会发生变化。
2.描述旋转时,要说明旋转中心、旋转方向和旋转角度。
3.在方格纸上画简单图形旋转90°后的图形:一要注意确定关键线段;二要明确旋转中心、旋转方向和旋转角度;三要注意对应线段的长度与相对位置不变;四要注意按原图的形状连接对应点
知识点二:图形的运动
1.图形的运动常见的方式有三种,分别是旋转、平移和轴对称。
2.图形平移时,注意移动的方向和距离。
3.画轴对称图形时,要注意各对应点到对称轴的距离相等。
4.图形在方格纸上旋转运动时,应找准旋转的中心、方向和角度。
5.逆用图形的运动可以将图形还原
知识点三:欣赏与设计
1.欣赏美丽的图案,要注意分析图案的构造,注意找出其中的基本图形,明确基本图形经过怎样的运动才能形成这幅图案。
2.可以单独利用图形的某一种运动方式设计图案,也可以综合运用两种或多种运动方式设计图案。
3.利用图形的变换方式设计图案时,首先要选好基本图形,然后确定运动方式,最后画出变换后的图案
一、精挑细选(共5题;每题1分,共5分)
1.
如图,三角形ABC怎样旋转可以得到三角形A'BC'?下面说法正确的是(???
)
A.?绕B点逆时针旋转90°??????????????????????????????????????????B.?绕B点顺时针旋转90°
C.?绕C点顺时针旋转90°??????????????????????????????????????????D.?绕C点逆时针旋转180°
2.
以点C为中心旋转的图形是(???
)。
A.????????????B.????????????C.?
3.
如图,点A的位置用数对表示是(1,5)。线段OA绕点O按顺时针方向旋转90°,点A的对应点A’的位置用数对表示是(??
)。
A.?(5,5)???????????????????????????B.?(5,1)???????????????????????????C.?(4,1)???????????????????????????D.?(6,1)
4.
将图形
A(?
),可以得到图形B.
A.?向右平移3格,再绕O点逆时针旋转90°
B.?向右平移5格,再绕O点顺时针旋转90°
C.?向右平移3格,再绕O点顺时针旋转90°
5.
如图中,图形A变换到图形B,下列描述不正确的是(?
)
A.?图形A先向右平移4格,再向下平移2格,然后以直径所在的直线作轴对称图形得到图形B
B.?图形A先向下平移2格,再向右平移4格,然后以直径所在的直线作轴对称图形得到图形B
C.?图形A先以直径所在的直线作轴对称图形,再向下平移4格,再向右平移2格,得到图形B
D.?图形A先以直径所在的直线作轴对称图形,再向右平移4格,再向下平移2格,得到图形B
二、判断正误(共5题;每题1分,共5分)
6.
如图,图1先顺时针旋转90°,再向右平移6个格,就可以得到图2。(???
)
7.
一个图形顺时针旋转180°和逆时针旋转180°,所得到的两个图形正好重合。
8.
旋转中,对应点划过的痕迹是一条圆弧。
9.
每个旋转的图形都有一个旋转中心或一个旋转轴。
10.
图形旋转后所对应的一组线段的夹角是90°,说明这个图形旋转了90°。(
??)
三、仔细想,认真填(共10题;每空1分,共36分)
11.
(
5分
)
如图所示,图形A到图形B向________平移了________格,图形B绕点O________时针旋转________得到图形C,图形C还可以看作是图形B的________.
12.
如图,A点的位置是(7,8),B点的位置是(10,3),将三角形AOB绕点O逆时针旋转90°到一个新的三角形A'OB',那么,A点的对应点A'的位置是(________,
________),B点的对应点B'的位置是(________,________)
13.
如图,
图形①绕点O逆时针旋转90°,得到图形________;图形③绕点o逆时针旋转90°得到图形________。
14.
下图每个小正方形的边长表示1厘米。
(1)在正方形方格纸上有一个三角形ABC,请用数对表示出C点的位置________。
(2)这个三角形的面积是________平方厘米。
(3)画出这个三角形绕C点顺时针旋转90度,再向右平移8格后的图形。
15.
正方形绕对称轴的交点至少旋转________度后与原图形重合;长方形绕对称轴的交点至少旋转________度后与原图形重合。
16.
在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为________,这个定点称为________,转动的角为________。
17.
下面图形绕O点顺时针旋转90°后的图形是________,顺时针旋转180°的图形是________
18.
下图中的指针从C开始,顺时针旋转180°指向________,指针从D开始,逆时针旋转90°指向________。
A.点A?????????????
B.
点B?????
???????C
.点C???????????
D
.点D
19.
如图
(1)以直线MN为________作图形A的________,得到图形B。
(2)将图形B绕点O________旋转________,得到图形C。
(3)将图形C向________平移________格,得到图形D。
20.
按要求在方格纸上画图(每个小方格表示1平方厘米)
(1)先用数对表示图中A点位置是________,再画出把图中的三角形绕A点顺时针旋转90?后得到的图形。在旋转过程中,B点划过的路程有________厘米。
(2)按1:2画出圆缩小后的图形,缩小后的图形面积是原来的________。
四、解答问题(共5题;共30.5分)
21.
(
6.5分
)
操作实践,动手动脑。
(1)画出三角形AOB关于直线MN对称的图形。
(2)若B点的位置可以用(x,y)表示,则A点的位置为________。
(3)画出三角形AOB绕点A逆时针旋转90°后的图形。
22.
(
8分
)
(1)用数对表示C点的位置(________,________).
(2)将小旗图围绕A点顺时针旋转90°
(3)将平行四边形向上平移4格,再向右平移5格。
(4)将三角形按2:1的比放大。
23.
(
3分
)
下图中,图形A是如何变换得到图形B?
24.
(
6分
)
(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形。旋转后,B点的位置用数对表示是(??
,??
).
(2)按1:2的比画出三角形缩小后的图形。缩小后的三角形的面积是原来的
。
(3)如果1个小方格表示1平方厘米,在方格纸上设计一个面积是8平方厘米的轴对称图形,并画出它的一条对称轴。
25.
(
7分
)
按要求完成下面各题。
(1)把图中的长方形绕点A顺时针旋转90°,画出旋转后的图形。点B旋转后的对应点B’的位置用数对表示是_________。
(2)按1:2的比例画出三角形缩小后的图形。缩小后的三角形的面积是原来的
________。
(3)如果1个小方格表示1cm2
,
在方格纸上设计一个面积是8cm2的轴对称图形,并画出它的一条对称轴。
五、巧妙作图(共2题;共15分)
26.
(
6分
)
(1)以直线l为对称轴画出图形①的对称图形②。
(2)先将图形②向右平移4格,再以点O为中心逆时针旋转90?,得到图形③,画出图形③。
27.
(
9分
)
在方格纸上按要求完成作业。
(1)将图A向左平移5格。
(2)将图B按点O顺时针方向旋转90o。
(3)以直线L为对称轴,画出已知图形C的轴对称图形。
六、综合提升(共2题;共8.5分)
28.
(
4分
)
小动物们分别向哪个方向平移?平移几格才能吃到它们喜欢的食物?
(1)小兔先向________平移________格,再向________平移________格,吃到胡萝卜。
(2)小狗先向________平移________格,再向________平移________格,吃到骨头。
29.
(
4.5分
)
观察图形,填写空格。
(1)①号图形绕A点按________时针方向旋转了________°;
(2)②号图形绕________点按顺时针方向旋转了________°;
(3)③号图形绕________点按________时针方向旋转了90";
(4)④号图形绕________点按________时针方向旋转了________°。
一、精挑细选
1.B
解:B点没变,说明是绕B点旋转的;观察线段AB和A'B',线段AB顺时针旋转90°是A'B',所以
三角形ABC绕B点顺时针旋转90°
得到三角形A'BC'。
故答案为:B。
思路引导:旋转是图形绕某定点沿某方向移动。特点:大小、形状不变、方向和位置变化。一条线段的旋转和整个图形的旋转是一样的。
2.B
以点C为中心旋转的图形是B。
故答案为:B。
思路引导:绕点C旋转则,则旋转后的图形与原图形的点C重合。
3.B
解:如图
A′的位置用数对表示是(5,1)。
故答案为:B。
思路引导:先确定旋转中心,然后根据旋转方向和度数画出旋转后的图形,然后用数对表示A′,数对中第一个数表示列,第二个数表示行。
4.C
解:根据题干分析可得:图形A先向右平移3格,再绕点O顺时针旋转90度,即可得出图形B,
故选:C.
思路引导:观察图形,根据图形旋转和平移的方法可得:图形A先向右平移3格,再绕点O顺时针旋转90度,即可得出图形B,据此即可选择.此题考查了利用旋转和平移进行图形变换的方法的灵活应用.
5.C
解:如图,
图形A变换到图形B,下列描述不正确的是:
A、图形A先向右平移4格,再向下平移2格,然后以直径所在的直线作轴对称图形得到图形B,正确;
B、图形A先向下平移2格,再向右平移4格,然后以直径所在的直线作轴对称图形得到图形B,正确;
C、图形A先以直径所在的直线作轴对称图形,再向下平移4格,再向右平移2格,得到图形B;不正确;
D、图形A先以直径所在的直线作轴对称图形,再向右平移4格,再向下平移2格,得到图形B,正确.
故选:C.
思路引导:根据平移的特征和轴对称图形的特征,图形A先向右平移4格,再向下平移2格,然后以直径所在的直线作轴对称图形得到图形B;或图形A先向下平移2格,再向右平移4格;或图形A先以直径所在的直线作轴对称图形,再向下平移2格,再向右平移4格,得到图形B;图形A先以直径所在的直线作轴对称图形,再向右平移4格,再向下平移2格,得到图形B,此题主查考查平移、轴对称的特征.平移作图要注意:①方向;②距离.整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动.此题的错误所右就是没弄清平移的距离;求作一个几何图形关于某条直线对称的图形,可以转化为求作这个图形上的特征点关于这条直线对称的点,然后依次连结各对称点即可.
二、判断正误
6.错误
如图,图1先逆时针旋转90°,再向右平移6个格,就可以得到图2,原题说法错误.
故答案为:错误.
思路引导:此题主要考查图形的旋转和平移,图形的旋转,弄清旋转中心、旋转的方向和角度,观察可知,以笑脸上的一点A为旋转中心,笑脸绕点A逆时针旋转了90°;平移时,要注意平移的方向和格数,观察图中笑脸的对应点是向右平移了6格,那么这个图形就向右平移了6格,据此判断.
7.正确
解:一个图形按某一个固定点顺时针旋转180度和逆时针旋转180度,所得到的两个图形正好重合,原题说法正确.
故答案为:正确
思路引导:顺时针和逆时针旋转180°,图形都是正好颠倒位置,只是运动的方向不同,所得到的图形是重合的.
8.正确
解:旋转中,对应点划过的痕迹是一条圆弧,原题说法正确.
故答案为:正确
思路引导:旋转中,对应的点划过的痕迹是一条圆弧,圆弧的圆心角就是旋转的度数.
9.正确
解:根据旋转图形的定义可知,每个旋转的图形都有一个旋转中心或一个旋转轴,原题说法正确.
故答案为:正确
思路引导:旋转是围绕着一个点或轴运动的,这个点就是旋转中心,这条轴就是旋转轴,由此判断即可.
10.正确
解:图形旋转后所对应的一组线段的夹角是90°,说明这个图形旋转了90°。原题说法正确。
故答案为:正确。
思路引导:旋转的度数就是旋转前后两个图形对应的线段之间的夹角,由此判断即可。
三、仔细想,认真填
11.右;4;顺;90°;轴对称图形
解:图形A到图形B向右平移了4格,图形B绕点O顺时针旋转90°得到图形C,图形C还可以看作图形B的轴对称图形。
故答案为:右;4;顺;90°;轴对称图形。
思路引导:平移,是指在平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。平移不改变图形的形状和大小。根
旋转:在平面内,把一个图形绕点O旋转一个角度的图形变换叫做旋转,点O叫做旋转中心,旋转的角叫做旋转角,如果图形上的点P经过旋转变为点Pˊ,那么这两个点叫做这个旋转的对应点。
轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。
12.2;3;7;6
解:如图:
A′的位置是(2,3),B′的位置是(7,6)。
故答案为:2,3;7,6。
思路引导:根据旋转中心、方向和度数画出旋转后的图形,然后根据两点所在的列与行用数对表示即可。
13.④;②
解:图形①绕点O逆时针旋转90°,得到图形④;图形③绕点O逆时针旋转90°得到图形②。
故答案为:④;②。
思路引导:旋转中心是O点,然后确定旋转方向,因为是旋转90°,所以对应边的夹角是直角,由此确定旋转后得到的图形即可。
14.(1)(3,4)(2)3
(1)C的位置是(3,4).
(2)三角形的面积:
2×3×
=6×
=3(平方厘米).
(3)根据分析,作图如下:
.
故答案为:(1)(3,4);(2)3;(3)
思路引导:(1)用数对表示位置时,第一个数字表示第几列,第二个数字表示第几行,中间用“,”隔开,据此解答;
(2)观察图可知,三角形的底是2厘米,高是3厘米,求三角形的面积,用公式:三角形的面积=底×高×
,
据此列式解答;
(3)画旋转图形的方法:按照旋转要求的方向,以这条线段为一条边,以旋转中心为顶点,画出旋转要求角度的角;在画出的这条射线上截取与已知线段相等长度的线段即为所求,据此画出旋转后的图形;然后向右平移8格,画出图形即可.
15.90;180
解:正方形绕对称轴的交点至少旋转90度后与原图形重合;长方形绕对称轴的交点至少旋转180度后与原图形重合。
故答案为:90;180。
思路引导:旋转时正方形一个顶点到相邻的另一个顶点时,就能与原图形重合;长方形的一个顶点到相对的顶点时才能与原图形重合。
16.旋转;旋转中心;旋转角
解:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角为旋转角.
故答案为:旋转;旋转中心;旋转角
思路引导:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角为旋转角.要掌握旋转三要素:旋转中心、旋转方向、旋转度数.
17.D;B
解:图形绕A点顺时针旋转90°后的图形开口向下,是图形D;
顺时针旋转180°开口向左,是图形B.
故答案为:D,B
思路引导:先确定旋转中心,再确定旋转方向和度数,注意抓住图形的主要特征来确定旋转后的图形.
18.B;C
解:指针从C开始,顺时针旋转180°成一条直线,指针指向B点;指针从D开始,逆时针旋转90°,和C点成直角,指向C点.
故答案为:B,C
思路引导:先确定旋转中心,再根据旋转方向和度数确定指针的指向;注意与钟面上指针转动的方向相同的是顺时针,与指针转动方向相反的是逆时针.
19.(1)对称轴;轴对称图形
(2)顺时针;90°
(3)右;六
解:(1)以直线MN对称轴作图形A的轴对称图形,得到图形B;
(2)将图形B绕点O顺时针旋转90°,得到图形C;
(3)将图形C像右平移六格,得到图形D.
故答案为:(1)对称轴;轴对称图形;(2)顺时针;90°;(3)右;六
思路引导:(1)图形A和B是以直线MN为轴对称的;(2)根据BC的位置确定旋转的方向和度数即可;(3)根据CD的位置确定平移的方向和格数即可.
20.(1)(4,7);12.56
(2)
(1)
先用数对表示图中A点位置是(4,7),再画出把图中的三角形绕A点顺时针旋转90?后得到的图形。在旋转过程中,B点划过的路程有2×4×3.14×=6.28厘米,作图如下:
;
(2)
按1:2画出圆缩小后的图形,缩小后的图形面积是原来的
,
作图如下:
.
故答案为:(1)(4,7);12.56;(2).
思路引导:(1)用数对表示位置时,第一个数字表示第几列,第二个数字表示第几行,中间用逗号隔开,据此表示出A点的位置;
要求画出图中的三角形绕A点顺时针旋转90?后得到的图形,弄清旋转中心、旋转的方向和角度,按照旋转要求的方向,以这条线段为一条边,以旋转中心为顶点,画出旋转要求角度的角;在画出的这条射线上截取与已知线段相等长度的线段即为所求,按原图连接各点即可;
观察可知,在旋转过程中,B点划过的痕迹是半径为4厘米的圆的弧长,先求出圆的周长,再乘即可;
(2)观察图形可知,原来的圆的半径是2厘米,要求按1:2画出圆缩小后的图形,先确定缩小后圆的半径,缩小后的圆的半径是1厘米,据此作图,然后分别求出缩小后的面积和原来圆的面积,最后相除即可得到缩小了多少,据此解答.
四、解答问题
21.(1)解:如图所示:
(2)(x+3,y+2)
(3)解:如图所示:
思路引导:(1)画轴对称图形的方法:①点出关键点,找出所有的关键点,即图形中所有线段的端点;②确定关键点到对称轴的距离,关键点离对称轴多远,对称点就离对称轴多远;③点出对称点;④连线,按照给出的一半图形将所有对称点连接成线段。
(2)用数对表示位置,先表示列,后表示行;
A点的位置为
(列数+3,行数+2)。
(3)
旋转作图,把一个图形绕其上面一点逆时针旋转一定的度数,先把这个点连接的边逆时针旋转指定的度数,然后把剩下的边连接起来即。
22.(1)2;8
(2)解:图形如下:
(3)解:图形如下:
(4)解:图形如下:
思路引导:(1)用数对表示点的位置时,这个点在第几列,数对中的第一个数字就写几,这个点在第几行,数对中的第二个数字就写几;
(2)把一个图形绕其上面一点,顺时针旋转一定的度数,先把这个点连接的边顺时针旋转相同的度数,然后把剩下的边连接起来即可;
(3)做平移后的图形,先把这个图形的关键点平移,然后把每条边连接起来即可;
(4)把一个图形按2:1的比放大,就是把这个图形的每条边都扩大2倍。
23.解:将图形A先向右平移5个格,再顺时针旋绕O点转90°即可得到图形B。
思路引导:观察两个图形的特征,需要进行一次平移,1次旋转才能得到图形B
,由此根据图形的特征描述变换方法即可。
24.(1)解:绕点A顺时针旋转90°得到图形1,如下图所示:
此时点B的位置为(7,6)。
(2)解:三角形按1:2的比例缩小后得到图形2,如下图所示:
三角形的面积=底×高÷2,底与高都缩小到原来的
,
则面积缩小到原来的×=。
(3)解:如图,图形3的面积是8平方厘米,它是一个长方形,它的对称轴有2条,分别是对边中点所在的直线。
思路引导:(1)画旋转图形的方法:把图形的每个点与旋转中心连接,再量出题目要求旋转的角度,最后依次连接;
用数对表示位置的方法是:第一个数字表示列,第二个数字表示行,中间用“,”隔开,据此解答;
(2)根据题意可知,先数一数原来直角三角形的两条直角边的格数,然后分别缩小到原来的
,
即可画出三角形缩小后的图形,三角形的面积=底×高÷2,当底和高都缩小到原来的
,
则缩小后的三角形的面积是原来的×=;
(3)根据题意可知,可以画一个长是4厘米,宽是2厘米的长方形,它的面积是8平方厘米,然后连接两条长的中点所在的直线就是它的一条对称轴,据此作图。
25.(1)图中蓝色的图形表示长方形旋转绕点A旋转90°后的图形,点B旋转后对应点B′的位置是(7,6)。
(2)假设每一个小正方形的边长为1,则大三角形的面积为:6×4÷2=12,缩小后三角形的面积为:3×2÷2=3,缩小后的三角形是原来的3÷12=。
答:缩小后的三角形如图形中的红色三角形。缩小后的三角形是原来的。
(3)轴对称图形有长方形、正方形、圆等等,以长方形为例,
面积是8cm2
则长方形长为4cm,宽为2cm,如图中的紫色图形,其中一条对称轴为长方形两条长边的中点的连线(如图中绿线)。
思路引导:(1)旋转:在平面内,把一个图形绕点O旋转一个角度的图形变换叫做旋转,点O叫做旋转中心,旋转的角叫做旋转角,如果图形上的点P经过旋转变为点Pˊ,那么这两个点叫做这个旋转的对应点。数对中的第一个数字表示列,第2个数字表示行,找出两个数字,中间用逗号隔开并用括号括起来;
(2)图形的缩小,即是按照比例将每一个边都缩小相同的倍数,原三角形的边长分别是6和4,缩小后三角形的边长分别是3和2,根据三角形的面积=底×高÷2,计算出原三角形和缩小后三角形的面积,再用缩小后的三角形面积除以原来三角形的面积即可得出答案;
(3)我们知道的轴对称图形有长方形、正方形、圆等等,以长方形为例,可得出面积为8cm2的长方形的长为4cm,宽为2cm,画出图形,找出它的对称轴即可。(沿对称轴折叠后图形两边完全重合)五、巧妙作图
26.(1)
(2)
思路引导:(1)画轴对称图形的方法是:数出或量出图形的关键点到对称轴的距离,在对称轴的另一侧找出关键点的对应点,按照所给图形的顺序连接各点;
(2)作平移图形的方法:先确定要平移图形的关键点,确定平移的方向是朝哪移的,然后确定移动的长度(格子数),最后把各点连接成图;
作旋转图形的方法:图形的旋转的关键是旋转中心、旋转方向和旋转的角度;画图时先弄清楚旋转的方向和角度,再确定从旋转点出发的两条线段旋转后的位置,这是关键所在,最后画其他的线段即可。
27.(1)
(2)
(3)
思路引导:(1)先确定平移的方向,然后根据平移的格数确定对应点的位置,再画出平移后的图形;
(2)先确定旋转中心,然后根据旋转方向和度数确定对应点的位置,然后画出旋转后的图形;
(3)轴对称图形对应点到对称轴的距离相等,先确定对应点的位置,再画出轴对称图形。
六、综合提升
28.(1)右;5;下;2
(2)上;4;左;3
解:(1)小兔先向右平移5格,再向下平移2格,吃到胡萝卜。
(2)小狗先向上平移4格,再向左平移3格,吃到骨头。
故答案为:(1)右;5;下;2;(2)上;4;左;3。(答案不唯一)
思路引导:平移,是指在平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。平移不改变图形的形状和大小。本题根据平移的特点进行解答。
29.(1)顺;90
(2)B;90
(3)C;逆
(4)D;顺;90
解:(1)①号图形绕A点按顺时针方向旋转了90°;
(2)②号图形绕B点按顺时针方向旋转了90°;
(3)③号图形绕C点按逆时针方向旋转了90°;
(4)④号图形绕D点按顺时针方向旋转了90°。
故答案为:(1)顺;90;(2)B;90;(3)C;逆;(4)D;顺;90。
思路引导:先确定旋转中心,然后判断旋转方向,根据对应边之间的夹角确定旋转度数即可。
知识互联网
知识导航
夯实基础
能力提升
能力达标百分训练(答案解析)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
