2020-2021学年北师大版数学六下第四单元《正比例和反比例》期中章节复习精编讲义(含解析)
文档属性
| 名称 | 2020-2021学年北师大版数学六下第四单元《正比例和反比例》期中章节复习精编讲义(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年北师大版数学六年级下册期中章节复习精编讲义
第四单元《正比例和反比例》
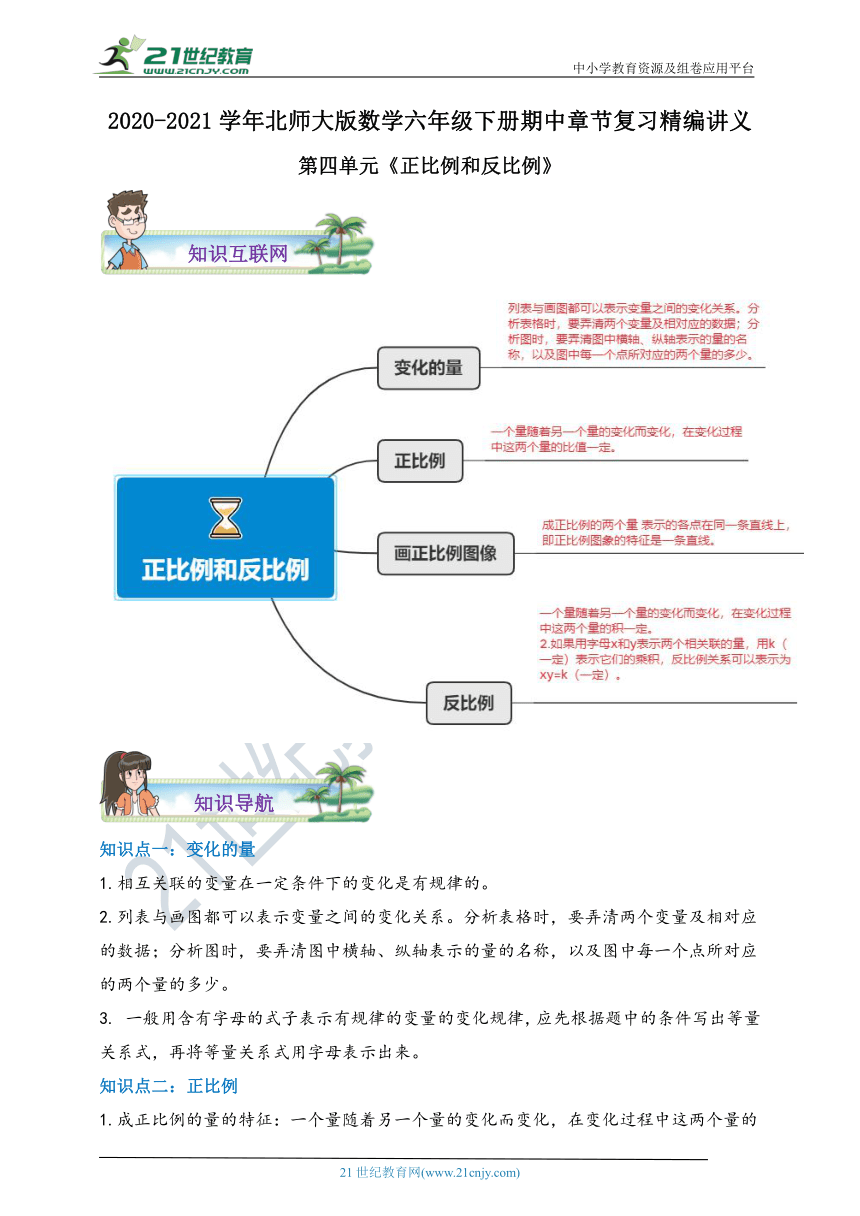
知识点一:变化的量
1.相互关联的变量在一定条件下的变化是有规律的。
2.列表与画图都可以表示变量之间的变化关系。分析表格时,要弄清两个变量及相对应的数据;分析图时,要弄清图中横轴、纵轴表示的量的名称,以及图中每一个点所对应的两个量的多少。
3.
一般用含有字母的式子表示有规律的变量的变化规律,应先根据题中的条件写出等量关系式,再将等量关系式用字母表示出来。
知识点二:正比例
1.成正比例的量的特征:一个量随着另一个量的变化而变化,在变化过程中这两个量的比值一定。
2.如果用x和y表示两个相关联的量,用k(一定)表示它们的比值,正比例关系可以表示为=k(一定)。
3.判断两个量是否成正比例的方法(1)首先,要确定这两个量是不是相关联的量(其中一个量是否随着另一个量的变化而变化);(2)其次,要根据两个变量之间的数值对应关系,计算出两个变量每一对数值的比值;(3)最后,根据比值是否一定来判断这两个变量是否成正比例。
知识点三:正比例图像
1.成正比例的两个量表示的各点在同一条直线上,即正比例图象的特征是一条直线。
2.从正比例图象中可以得出任意一点所表示的意义。
3.
观察正比例图象时,要先明确横轴、纵轴表示的意义,从图象中可以直观地看出两个量的变化情况,不需要计算,由一个量的值可以直接找到与它对应的另一个量的值。
知识点四:反比例
1.成反比例的量的特征:一个量随着另一个量的变化而变化,在变化过程中这两个量的积一定。
2.如果用字母x和y表示两个相关联的量,用k(一定)表示它们的乘积,反比例关系可以表示为xy=k(一定)。
3.判断两个量是否成反比例的方法
(1)首先,要确定这两个量是不是相关联的量(其中一个量是否随着另一个量的变化而变化);
(2)其次,要根据两个变量之间的数值对应关系,计算出两个变量每一对数值的积;
(3)最后,根据积是否一定来判断这两个变量是否成反比例。
4.
正比例和反比例的异同点
一、精挑细选(共5题;每题2分,共10分)
1.
下列各数量关系中,成正比例关系的是(??
)
A.?总价一定,买的数量与单价????????????????????????????????B.?全班人数一定,出勤人数与缺勤人数
C.?圆的周长与它的半径??????????????????????????????????????????D.?运送一批货物,平均每天运的吨数和需要的天数
2.
下面两个量,成正比例的(???
)
A.?圆锥体积不变,它的底面积和高。??????????????????????B.?路程一定,已走的路程和未走的路程。
C.?两地的实际距离不变,比例尺和图上距离。????????D.?分子一定,分数值和分母(不为0)
3.
表示x和y成反比例关系的式子是(???
)。
A.?y=3x????????????????????????????????B.?
=y????????????????????????????????C.?x+y=18????????????????????????????????D.?x-y=18
4.
用比例解.
用电锯把一根木料锯成5段,需要48分钟.照这样计算,如果把这根木料锯成8段,要用(??
)
A.?80分钟???????????????????????????????B.?48分钟???????????????????????????????C.?84分钟???????????????????????????????D.?90分钟
5.
同时同地,一根长1米的标杆的影长0.6米,一名修理工要爬至48米高的电视塔上修理设备,他竖直方向爬行的速度为0.4米/秒,则此人的影子移动的速度为( )米/秒.
A.?0.56?????????????????????????????????????B.?0.24?????????????????????????????????????C.?0.48?????????????????????????????????????D.?0.36
二、判断正误(共5题;每题2分,共10分)
6.)
=
(x和y均不为0),x和y成正比例关系。(???
)
7.
正方形的边长和面积成正比例。(???
)
8.
一辆汽车从杨家坪开往云阳,汽车行驶的速度与时间成正比例。(??
)
9.
圆的半径越大,面积也就越大,所以圆的半径和面积成正比例。
10.
圆柱的体积一定,圆柱的底面积与高成反比例关系。(???
)
三、仔细想,认真填(共8题;每空1分,共16分)
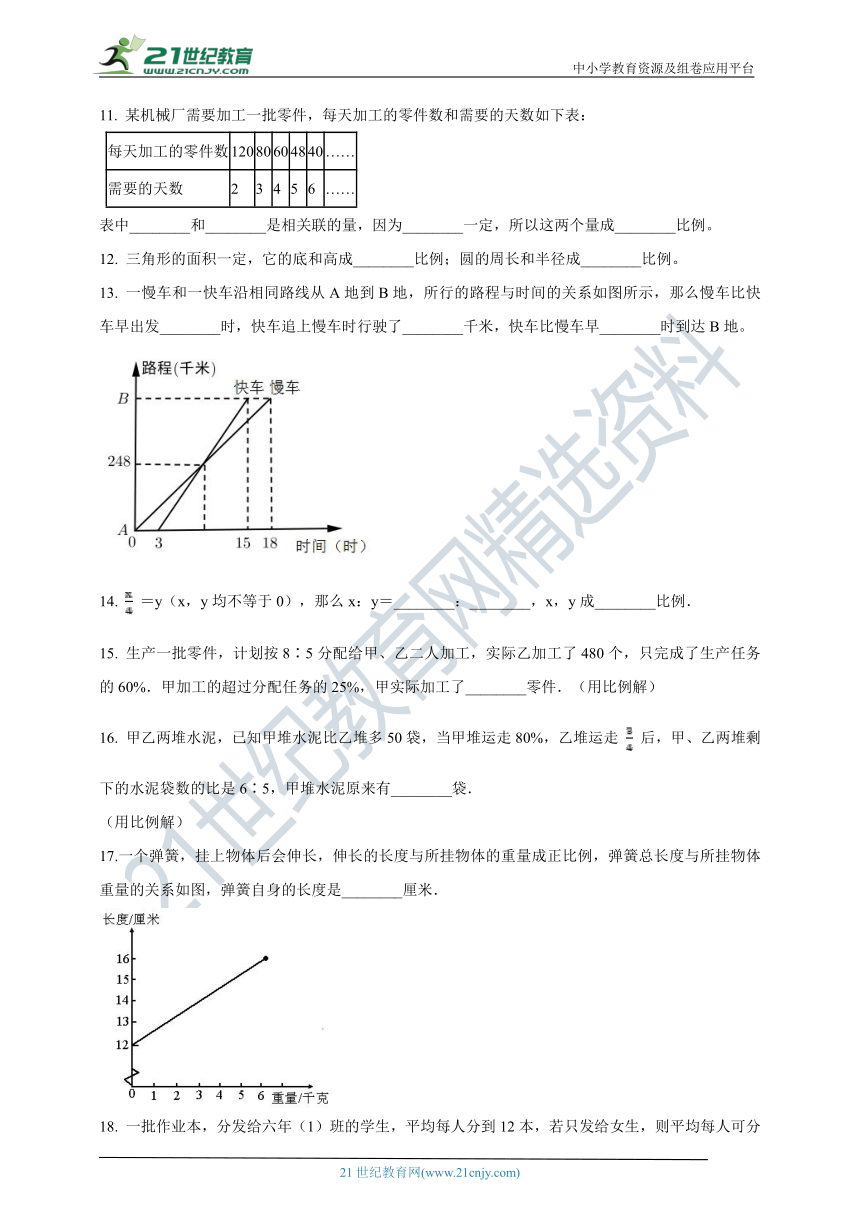
11.
某机械厂需要加工一批零件,每天加工的零件数和需要的天数如下表:
每天加工的零件数
120
80
60
48
40
……
需要的天数
2
3
4
5
6
……
表中________和________是相关联的量,因为________一定,所以这两个量成________比例。
12.
三角形的面积一定,它的底和高成________比例;圆的周长和半径成________比例。
13.
一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的关系如图所示,那么慢车比快车早出发________时,快车追上慢车时行驶了________千米,快车比慢车早________时到达B地。
14.
=y(x,y均不等于0),那么x:y=________:________,x,y成________比例.
15.
生产一批零件,计划按8∶5分配给甲、乙二人加工,实际乙加工了480个,只完成了生产任务的60%.甲加工的超过分配任务的25%,甲实际加工了________零件.(用比例解)
16.
甲乙两堆水泥,已知甲堆水泥比乙堆多50袋,当甲堆运走80%,乙堆运走
后,甲、乙两堆剩下的水泥袋数的比是6∶5,甲堆水泥原来有________袋.
(用比例解)
17.一个弹簧,挂上物体后会伸长,伸长的长度与所挂物体的重量成正比例,弹簧总长度与所挂物体重量的关系如图,弹簧自身的长度是________厘米.
18.
一批作业本,分发给六年(1)班的学生,平均每人分到12本,若只发给女生,则平均每人可分到20本,若只发给男生,平均每人可分到________本。
四、综合提升(共3题;共21分)
19.
(
6分
)
??????
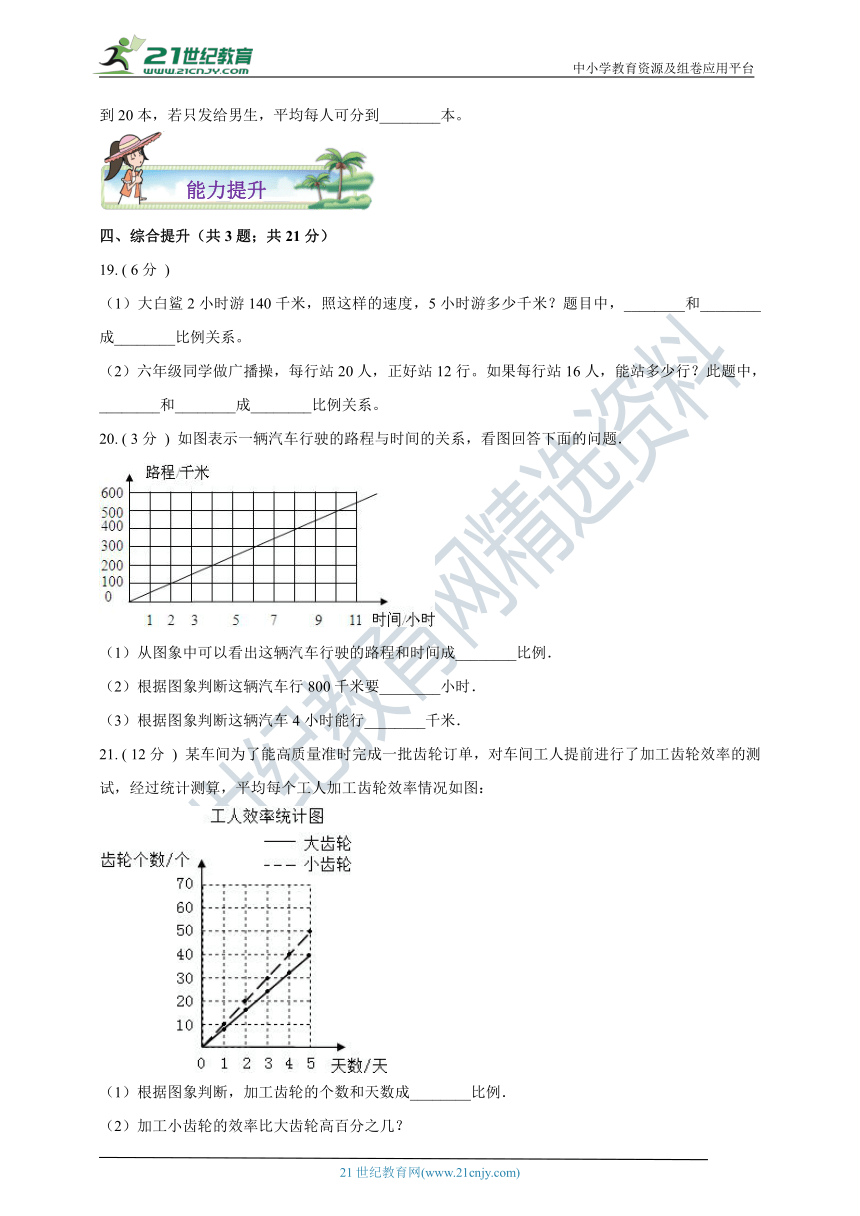
(1)大白鲨2小时游140千米,照这样的速度,5小时游多少千米?题目中,________和________成________比例关系。
(2)六年级同学做广播操,每行站20人,正好站12行。如果每行站16人,能站多少行?此题中,________和________成________比例关系。
20.
(
3分
)
如图表示一辆汽车行驶的路程与时间的关系,看图回答下面的问题.
(1)从图象中可以看出这辆汽车行驶的路程和时间成________比例.
(2)根据图象判断这辆汽车行800千米要________小时.
(3)根据图象判断这辆汽车4小时能行________千米.
21.
(
12分
)
某车间为了能高质量准时完成一批齿轮订单,对车间工人提前进行了加工齿轮效率的测试,经过统计测算,平均每个工人加工齿轮效率情况如图:
(1)根据图象判断,加工齿轮的个数和天数成________比例.
(2)加工小齿轮的效率比大齿轮高百分之几?
(3)已知这个车间有工人85人,1个大齿轮和3个小齿轮配为一套,为了使大小齿轮能成套出厂,如果你是车间主任,怎样安排这85名工人最合理?
五、解答问题(共7题;共43分)
22.
(
6分
)
在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2
4
9
16
所需小正方形的数量/个
216
96
54
(1)每个小正方形的面积与所需小正方形的数量成________比例关系.
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
23.
(
5分
)
陈师傅要加工221个零件,6小时加工了78个零件。照这样的速度,还要加工几小时才能完成任务?(用比例解答)
24.
(
10分
)
??
(1)一辆汽车,每百千米耗油8L。照这样计算,王叔叔驾驶该汽车从甲地出发去相距80km的乙地,需要用多少升油?
(2)一辆汽车,每百千米耗油8L。照这样计算,王叔叔驾驶该汽车从甲地出发去乙地,共耗油6.4L。甲地与乙地相距多少千米?
25.
(
5分
)
有一批树苗,原计划40人去栽,每人要栽15棵,后来增加10人去栽,每人要栽多少棵?
26.
(
5分
)
学校要给图书室的地面铺上方砖,如果用边长为30cm的方砖铺,需要600块,如果改用边长为60cm的方砖铺,需要多少块?
27.
(
5分
)
一个工厂运来一批煤,计划每天烧8吨,可以烧45天。实际每天节约用煤10%,这样可以多烧多少天?
28.
(
7分
)
一列动车在高速铁路上行驶的时间和路程如图。
(1)看图填写下表。
时间/小时
3
路程/千米
?
?
?
800?
?
?
?
(2)这列动车行驶的时间和路程成________比例。
(3)照这样的速度,行1800千米需要________小时。
一、精挑细选
1.
C
A选项,数量×单价=总价(一定),乘积一定,那么数量和单价成反比例,所以A错误。
B选项,出勤人数+缺勤人数=全班总人数(一定),和一定,那么出勤人数和缺勤人数不成比例,所以B错误。
C选项,=2π(一定),比值一定,那么
圆的周长与它的半径成正比例,所以C正确。
D选项,
平均每天运的吨数×需要的天数=这批货物的重量(一定),乘积一定,那么平均每天运的吨数和需要的天数成反比例,所以D错误。
故答案为:C。
思路引导:两种相关联的量,一种量随着另一种量的变化而变化,如果这两种量的比值一定,那么这两种量成正比例关系;如果这两种量的乘积一定,那么这两种量成反比例关系。
2.
C
解:A:圆锥的底面积×高=圆锥的体积×3(一定),底面积和高成反比例;
B:已走的路程+未走的路程=路程,二者的和一定,不成比例;
C:图上距离÷比例尺=实际距离(一定),二者成正比例;
D:分数值×分母=分子(一定),二者成反比例。
故答案为:C。
思路引导:根据数量关系以及公式判断出相关联的两个量的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例。
3.
B
解:A项中,x和y成正比例;
B项中,x和y成反比例;
C项和D项中,x和y不成比例关系。
故答案为:B。
思路引导:若y=(k为常数,x,y≠0),那么x和y成反比例。
4.
C
解:设要用x分钟,
48:(5-1)=x:(8-1)
????????
4x=48×7
??????????
x=336÷4
??????????
x=84
故答案为:C
思路引导:锯成5段需要锯(5-1)次,锯成8段需要锯(8-1)次;锯的总时间与次数成正比例,设出未知数,根据每锯一次的时间不变列出比例解答即可.
5.
B
解:设此人的影子移动的速度为x米/秒.
0.6:1=x:0.4,
????
x=0.6×0.4,
????
x=0.24,
答:此人的影子移动的速度为0.24米/秒.
故选:B.
思路引导:因为在时间相同时,速度比等于路程的比,所以再根据在同时同地,影子的长度与物体的实际长度的比值一定,所以影子的长度与物体的实际长度成正比例,由此列出比例解答即可.
二、判断正误
6.
错误
解:=
xy=3×4
xy=12(一定),积一定,
x和y成反比例关系。
故答案为:错误。
思路引导:x和y这两数的乘积一定,成反比例关系。
7.
错误
正方形的面积与边长的比值比一定,所以正方形的边长和面积不成正比例。
故答案为:错误。
思路引导:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关系叫做正比例关系。用字母表示=k(一定)。
8.
错误
一辆汽车从杨家坪开往云阳,汽车行驶的速度与时间成反比例。原说法错误。
故答案为:错误。
思路引导:速度×时间=路程(一定),速度与时间成反比例。
9.
错误
因为圆的面积÷半径=圆周率×半径,这里圆周率×半径不能确定,所以圆的面积与半径不成比例,原题说法错误。
故答案为:错误。
思路引导:
如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y:x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
10.
正确
圆柱底面积×高=圆柱的体积(一定),即
圆柱的体积一定,圆柱的底面积与高成反比例关系?。
故答案为:正确
思路引导:反比例关系式为:x×y=k(一定),因此,圆柱的体积一定时,圆柱的底面积与高成反比例关系。
三、仔细想,认真填
11.
每天加工的零件数;需要的天数;每天加工的零件数和需要的天数乘积;反
表中每天加工的零件数和需要的天数是相关联的量,因为每天加工的零件数和需要的天数的乘积一定,所以这两个量成反比例。
故答案为:每天加工的零件数;需要的天数;每天加工的零件数和需要的天数乘积;反。
思路引导:表中每天加工的零件数随着需要的天数的增多而减少,所以每天加工的零件数和需要的天数是相关联的量,且120×2=240,80×3=240,60×4=240,48×5=240,40×6=240……,所以每天加工的零件数×需要的天数=总零件数(一定),乘积一定,因此这两个量成反比例。
12.
反;正
解:底×高=三角形面积×2(一定),三角形面积一定,它的底和高成反比例;
圆的周长÷半径=2(一定),圆的周长和半径成正比例。
故答案为:反;正。
思路引导:根据三角形面积公式和圆周长公式判断相关联的两个量的乘积一定还是商一定,如果乘积一定就成反比例,如果商一定就成正比例,否则不成比例。
13.
3;248;3
解:有图象可知:慢车比快车早出发3小时;快车追上慢车时行驶了248千米;
18-15=3(小时)
快车比慢车早3小时到达B地。
故答案为:3;248;3。
思路引导:所行的路程与时间的关系如图所示,横轴表示时间,纵轴表示路程,慢车从0时开始行驶,快车从3时开始行驶,所以慢车比快车早出发3小时;当快车和慢车行驶的路程相交时是248千米,所以快车追上慢车时行驶了248千米;快车15时到达,慢车18时到达,所以快车比慢车早3小时到达B地。
14.
4;1;正
解:x:y=4:1;x,y成正比例。
故答案为:4;1;正。
思路引导:=y,所以x=4y,所以x:y=4:1;
当xy=k(k为常数,x,y≠0)时,x和y成正比例关系。
15.
1600
解:设甲实际加工了x个零件,
[x÷(1+25%)]:(480÷60%)=8:5
??????????????????
?
?
?
?
?
x×5=800×8
???????????????????????
?
?
?
?
??
4x=6400
???????????????????????????
?
?
?
??
x=6400÷4
?????????????????????????????
?
??
?
x=1600
故答案为:1600
思路引导:设甲实际加工了x个零件,那么甲的任务就是x÷(1+25%),乙的任务是480÷60%,根据两人的任务比是8:5列出比例解答即可.
16.
150
解:设甲堆水泥原来有x袋.
0.2x×5=0.25(x-50)×6
x=1.5x-75
0.5x=75
x=150
故答案为:150
思路引导:设甲堆水泥原来有x袋,则乙堆水泥有(x-50)袋;甲剩下的水泥:(1-80%)x袋,乙剩下的水泥:(1-)(x-50)袋,根据甲、乙两堆剩下的水泥袋数的比是6:5列出比例解答即可.
17.
12
解:当重量是0千克时,弹簧的长度是12厘米,所以弹簧自身的长度就是12厘米.
故答案为:12
思路引导:横轴表示重量,纵轴表示弹簧长度,判断出重量为0时弹簧的长度就是弹簧自身的长度.
18.
30
因为总本书一定,则人数与每人分得的本数成反比例,
20×女=12×总,
女=总。
设总人数为5份,则女生为3份,男生为2份。
设男生平均每人可分得x本,可得:
x×2份=20×3份
?
?
?
?
?x=30
所以只发给男生,平均每人可分得30本。
故答案为:30.
思路引导:作业本总数一定,20×女生数=12×总人数,男生数×男生平均每人本数=女生数×20。
四、综合提升
19.
(1)路程;时间;正
(2)每行站的人数;站的行数;反
解:(1)路程÷时间=速度(一定);题目中,路程和时间成正比例关系;
(2)每行站的人数×站的行数=学生总人数(一定);每行站的人数和站的行数成反比例关系。
故答案为:(1)路程;时间;正;(2)每行站的人数;站的行数;反。
思路引导:(1)正比例的判断方法:相关联,能变化,商一定;
(2)反比例的判断方法:相关联,能变化,积一定。
20.
(1)正(2)16(3)200
解:(1)从图象中可以看出这辆汽车行驶的路程和时间成正比例;
(2)100÷2=50千米,800÷50=16小时,所以这辆汽车行800千米要16小时;
(3)100÷2=50千米,50×4=200千米,所以这辆汽车4小时能行200千米。
思路引导:(1)从图中看出,图像是从0开始呈直线上升,所以这辆汽车行驶的路程和时间成正比例关系;
(2)这辆汽车的速度=这辆汽车2小时行驶的距离÷2,那么这辆汽车行800千米要的时间=800÷速度;
(3)这辆汽车4小时能行驶的距离=速度×4。
21.
(1)正
(2)解:(50÷5﹣40÷5)÷(40÷5);
=2÷8,
=25%;
答:加工小齿轮的效率比大齿轮高25%
(3)解:①每人每天加工小齿轮的个数如下:50÷5=10(个),②每人每天加工大齿轮的个数如下:40÷5=8(个),③设加工小齿轮的人数是x人,则加工大齿轮的人数为(85﹣x).8×(85﹣x)=10×x÷3,
680﹣8x=
,680﹣8x+8x=
+8x,
+
=680,
=680,
×
=680×
,
x=60;加工大齿轮的人数是:85﹣x=85﹣60=25(人);答:加工大齿轮的人数是25人,加工小齿轮的人数是60人.
解:(1)据图象判断,加工齿轮的个数和天数成正比例.
思路引导:(1)根据图象判断,加工齿轮的个数随着加工的时间增加而增多.(2)相同的时间内,加工小齿轮的个数比大齿轮多的是大齿轮百分之几.(3)先求出每个工人每天加工大齿轮、小齿轮各加工几个,再设出加工大、小齿轮的人数,然后在运用方程解答.本题借助折线统计图考查了学生两个量成比例问题,一个数比另一个数多百分之几的问题,同时考查了工作量与人数分配问题.只要认真思考,就能正确的解答.
五、解答问题
22.
(1)反
(2)解:设需要多x个小正方形.
???????
36x=216×4
36x÷36=216×4÷36
?????????
x=24
答:需要24个小正方形。
思路引导:(1)经过计算,每个小正方形的面积×所需小正方形的数量是一个定值,所以每个小正方形的面积与所需小正方形的数量成反比例关系;
(2)本题可以设需要x个小正方形,题中存在的比例关系是:36×需要面积是36cm2的小正方形的个数=4×需要面积是4cm2的小正方形的个数,据此代入数据和字母作答即可。
23.
解:设还要加工x小时才能完成任务。
????????????
78(6+x)=221×6
??
468+78x=1326
???????????
78x=1326-468
???????????
78x=858
???????????????
x=858÷78
???????????????
x=11
答:还要加工11小时才能完成任务。
思路引导:工作总量÷工作时间=工效(一定),列出正比例,解比例。
24.
(1)解:设需要用x升油。
8:100=x:80
???
100x=8×80
??
100x=640
????????
x=640÷100
????????
x=6.4
答:需要用6.4升油。
(2)解:设甲地与乙地相距x千米。
100:8=x:6.4
?????
?
8x=100×6.4
???????
8x=640
?????????
x=640÷8
?????????
x=80
答:甲地与乙地相距80千米。
思路引导:(1)8升油:百千米=需要油的升数:行驶的路程;
(2)百千米路程:8升=甲地与乙地距离:共耗油升数。
25.
解:设每人要栽x棵。
(40+10)x=40×15
?
?
?
?
?
?
?50x=600
?
?
?
?
?
?
?
?
?x=600÷50
?
?
?
?
?
?
?
?
?x=12
答:每人要栽12棵。
思路引导:每人栽的棵数×人数=总棵数,每人栽的棵数与人数成反比例,设出未知数,根据总棵数不变列出比例,解比例求出每人要栽的棵数。
26.
解:设需要x块。
602x=302×600
x=150
解:设需要x块。
60?x=30?×600
360x=540000
?
?
?
x=540000÷360
?
?
?
x=150
答:需要150块。
思路引导:每块的面积×块数=图书室总面积,总面积不变,每块面积与块数成反比例,设出未知数,根据总面积不变列出比例解答即可。
27.
解:8×45÷[8×(1-10%)]
=360÷[8×0.9]
=360÷7.2
=50(天)
50-45=5(天)
答:这样可以多烧5天?。
思路引导:煤总数=计划每天烧的数量×计划天数,实际每天烧的数量=计划每天烧的数量×(1-10%)
实际天数=煤总数÷实际每天烧的数量,多烧天数=实际天数-计划天数。
28.
(1)
时间/小时
3
4
路程/千米
600?
?
?
??
800?
?
?
?
(2)正(3)9
(2)路程÷时间=200(一定),行驶的时间和路程成正比例;
(3)1800÷200=9(小时)。
故答案为:(2)正;(3)9。
思路引导:(1)图中横轴表示时间,竖轴表示路程,根据图形直接判断3小时行驶的路程,800千米需要的时间;
(2)根据时间和路程相对应的数据确定路程和时间的比值一定,二者就成正比例关系;
(3)用路程除以速度即可求出行驶的时间。
知识互联网
知识导航
夯实基础
能力提升
能力达标百分训练(答案解析)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年北师大版数学六年级下册期中章节复习精编讲义
第四单元《正比例和反比例》
知识点一:变化的量
1.相互关联的变量在一定条件下的变化是有规律的。
2.列表与画图都可以表示变量之间的变化关系。分析表格时,要弄清两个变量及相对应的数据;分析图时,要弄清图中横轴、纵轴表示的量的名称,以及图中每一个点所对应的两个量的多少。
3.
一般用含有字母的式子表示有规律的变量的变化规律,应先根据题中的条件写出等量关系式,再将等量关系式用字母表示出来。
知识点二:正比例
1.成正比例的量的特征:一个量随着另一个量的变化而变化,在变化过程中这两个量的比值一定。
2.如果用x和y表示两个相关联的量,用k(一定)表示它们的比值,正比例关系可以表示为=k(一定)。
3.判断两个量是否成正比例的方法(1)首先,要确定这两个量是不是相关联的量(其中一个量是否随着另一个量的变化而变化);(2)其次,要根据两个变量之间的数值对应关系,计算出两个变量每一对数值的比值;(3)最后,根据比值是否一定来判断这两个变量是否成正比例。
知识点三:正比例图像
1.成正比例的两个量表示的各点在同一条直线上,即正比例图象的特征是一条直线。
2.从正比例图象中可以得出任意一点所表示的意义。
3.
观察正比例图象时,要先明确横轴、纵轴表示的意义,从图象中可以直观地看出两个量的变化情况,不需要计算,由一个量的值可以直接找到与它对应的另一个量的值。
知识点四:反比例
1.成反比例的量的特征:一个量随着另一个量的变化而变化,在变化过程中这两个量的积一定。
2.如果用字母x和y表示两个相关联的量,用k(一定)表示它们的乘积,反比例关系可以表示为xy=k(一定)。
3.判断两个量是否成反比例的方法
(1)首先,要确定这两个量是不是相关联的量(其中一个量是否随着另一个量的变化而变化);
(2)其次,要根据两个变量之间的数值对应关系,计算出两个变量每一对数值的积;
(3)最后,根据积是否一定来判断这两个变量是否成反比例。
4.
正比例和反比例的异同点
一、精挑细选(共5题;每题2分,共10分)
1.
下列各数量关系中,成正比例关系的是(??
)
A.?总价一定,买的数量与单价????????????????????????????????B.?全班人数一定,出勤人数与缺勤人数
C.?圆的周长与它的半径??????????????????????????????????????????D.?运送一批货物,平均每天运的吨数和需要的天数
2.
下面两个量,成正比例的(???
)
A.?圆锥体积不变,它的底面积和高。??????????????????????B.?路程一定,已走的路程和未走的路程。
C.?两地的实际距离不变,比例尺和图上距离。????????D.?分子一定,分数值和分母(不为0)
3.
表示x和y成反比例关系的式子是(???
)。
A.?y=3x????????????????????????????????B.?
=y????????????????????????????????C.?x+y=18????????????????????????????????D.?x-y=18
4.
用比例解.
用电锯把一根木料锯成5段,需要48分钟.照这样计算,如果把这根木料锯成8段,要用(??
)
A.?80分钟???????????????????????????????B.?48分钟???????????????????????????????C.?84分钟???????????????????????????????D.?90分钟
5.
同时同地,一根长1米的标杆的影长0.6米,一名修理工要爬至48米高的电视塔上修理设备,他竖直方向爬行的速度为0.4米/秒,则此人的影子移动的速度为( )米/秒.
A.?0.56?????????????????????????????????????B.?0.24?????????????????????????????????????C.?0.48?????????????????????????????????????D.?0.36
二、判断正误(共5题;每题2分,共10分)
6.)
=
(x和y均不为0),x和y成正比例关系。(???
)
7.
正方形的边长和面积成正比例。(???
)
8.
一辆汽车从杨家坪开往云阳,汽车行驶的速度与时间成正比例。(??
)
9.
圆的半径越大,面积也就越大,所以圆的半径和面积成正比例。
10.
圆柱的体积一定,圆柱的底面积与高成反比例关系。(???
)
三、仔细想,认真填(共8题;每空1分,共16分)
11.
某机械厂需要加工一批零件,每天加工的零件数和需要的天数如下表:
每天加工的零件数
120
80
60
48
40
……
需要的天数
2
3
4
5
6
……
表中________和________是相关联的量,因为________一定,所以这两个量成________比例。
12.
三角形的面积一定,它的底和高成________比例;圆的周长和半径成________比例。
13.
一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的关系如图所示,那么慢车比快车早出发________时,快车追上慢车时行驶了________千米,快车比慢车早________时到达B地。
14.
=y(x,y均不等于0),那么x:y=________:________,x,y成________比例.
15.
生产一批零件,计划按8∶5分配给甲、乙二人加工,实际乙加工了480个,只完成了生产任务的60%.甲加工的超过分配任务的25%,甲实际加工了________零件.(用比例解)
16.
甲乙两堆水泥,已知甲堆水泥比乙堆多50袋,当甲堆运走80%,乙堆运走
后,甲、乙两堆剩下的水泥袋数的比是6∶5,甲堆水泥原来有________袋.
(用比例解)
17.一个弹簧,挂上物体后会伸长,伸长的长度与所挂物体的重量成正比例,弹簧总长度与所挂物体重量的关系如图,弹簧自身的长度是________厘米.
18.
一批作业本,分发给六年(1)班的学生,平均每人分到12本,若只发给女生,则平均每人可分到20本,若只发给男生,平均每人可分到________本。
四、综合提升(共3题;共21分)
19.
(
6分
)
??????
(1)大白鲨2小时游140千米,照这样的速度,5小时游多少千米?题目中,________和________成________比例关系。
(2)六年级同学做广播操,每行站20人,正好站12行。如果每行站16人,能站多少行?此题中,________和________成________比例关系。
20.
(
3分
)
如图表示一辆汽车行驶的路程与时间的关系,看图回答下面的问题.
(1)从图象中可以看出这辆汽车行驶的路程和时间成________比例.
(2)根据图象判断这辆汽车行800千米要________小时.
(3)根据图象判断这辆汽车4小时能行________千米.
21.
(
12分
)
某车间为了能高质量准时完成一批齿轮订单,对车间工人提前进行了加工齿轮效率的测试,经过统计测算,平均每个工人加工齿轮效率情况如图:
(1)根据图象判断,加工齿轮的个数和天数成________比例.
(2)加工小齿轮的效率比大齿轮高百分之几?
(3)已知这个车间有工人85人,1个大齿轮和3个小齿轮配为一套,为了使大小齿轮能成套出厂,如果你是车间主任,怎样安排这85名工人最合理?
五、解答问题(共7题;共43分)
22.
(
6分
)
在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2
4
9
16
所需小正方形的数量/个
216
96
54
(1)每个小正方形的面积与所需小正方形的数量成________比例关系.
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
23.
(
5分
)
陈师傅要加工221个零件,6小时加工了78个零件。照这样的速度,还要加工几小时才能完成任务?(用比例解答)
24.
(
10分
)
??
(1)一辆汽车,每百千米耗油8L。照这样计算,王叔叔驾驶该汽车从甲地出发去相距80km的乙地,需要用多少升油?
(2)一辆汽车,每百千米耗油8L。照这样计算,王叔叔驾驶该汽车从甲地出发去乙地,共耗油6.4L。甲地与乙地相距多少千米?
25.
(
5分
)
有一批树苗,原计划40人去栽,每人要栽15棵,后来增加10人去栽,每人要栽多少棵?
26.
(
5分
)
学校要给图书室的地面铺上方砖,如果用边长为30cm的方砖铺,需要600块,如果改用边长为60cm的方砖铺,需要多少块?
27.
(
5分
)
一个工厂运来一批煤,计划每天烧8吨,可以烧45天。实际每天节约用煤10%,这样可以多烧多少天?
28.
(
7分
)
一列动车在高速铁路上行驶的时间和路程如图。
(1)看图填写下表。
时间/小时
3
路程/千米
?
?
?
800?
?
?
?
(2)这列动车行驶的时间和路程成________比例。
(3)照这样的速度,行1800千米需要________小时。
一、精挑细选
1.
C
A选项,数量×单价=总价(一定),乘积一定,那么数量和单价成反比例,所以A错误。
B选项,出勤人数+缺勤人数=全班总人数(一定),和一定,那么出勤人数和缺勤人数不成比例,所以B错误。
C选项,=2π(一定),比值一定,那么
圆的周长与它的半径成正比例,所以C正确。
D选项,
平均每天运的吨数×需要的天数=这批货物的重量(一定),乘积一定,那么平均每天运的吨数和需要的天数成反比例,所以D错误。
故答案为:C。
思路引导:两种相关联的量,一种量随着另一种量的变化而变化,如果这两种量的比值一定,那么这两种量成正比例关系;如果这两种量的乘积一定,那么这两种量成反比例关系。
2.
C
解:A:圆锥的底面积×高=圆锥的体积×3(一定),底面积和高成反比例;
B:已走的路程+未走的路程=路程,二者的和一定,不成比例;
C:图上距离÷比例尺=实际距离(一定),二者成正比例;
D:分数值×分母=分子(一定),二者成反比例。
故答案为:C。
思路引导:根据数量关系以及公式判断出相关联的两个量的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例。
3.
B
解:A项中,x和y成正比例;
B项中,x和y成反比例;
C项和D项中,x和y不成比例关系。
故答案为:B。
思路引导:若y=(k为常数,x,y≠0),那么x和y成反比例。
4.
C
解:设要用x分钟,
48:(5-1)=x:(8-1)
????????
4x=48×7
??????????
x=336÷4
??????????
x=84
故答案为:C
思路引导:锯成5段需要锯(5-1)次,锯成8段需要锯(8-1)次;锯的总时间与次数成正比例,设出未知数,根据每锯一次的时间不变列出比例解答即可.
5.
B
解:设此人的影子移动的速度为x米/秒.
0.6:1=x:0.4,
????
x=0.6×0.4,
????
x=0.24,
答:此人的影子移动的速度为0.24米/秒.
故选:B.
思路引导:因为在时间相同时,速度比等于路程的比,所以再根据在同时同地,影子的长度与物体的实际长度的比值一定,所以影子的长度与物体的实际长度成正比例,由此列出比例解答即可.
二、判断正误
6.
错误
解:=
xy=3×4
xy=12(一定),积一定,
x和y成反比例关系。
故答案为:错误。
思路引导:x和y这两数的乘积一定,成反比例关系。
7.
错误
正方形的面积与边长的比值比一定,所以正方形的边长和面积不成正比例。
故答案为:错误。
思路引导:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关系叫做正比例关系。用字母表示=k(一定)。
8.
错误
一辆汽车从杨家坪开往云阳,汽车行驶的速度与时间成反比例。原说法错误。
故答案为:错误。
思路引导:速度×时间=路程(一定),速度与时间成反比例。
9.
错误
因为圆的面积÷半径=圆周率×半径,这里圆周率×半径不能确定,所以圆的面积与半径不成比例,原题说法错误。
故答案为:错误。
思路引导:
如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y:x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
10.
正确
圆柱底面积×高=圆柱的体积(一定),即
圆柱的体积一定,圆柱的底面积与高成反比例关系?。
故答案为:正确
思路引导:反比例关系式为:x×y=k(一定),因此,圆柱的体积一定时,圆柱的底面积与高成反比例关系。
三、仔细想,认真填
11.
每天加工的零件数;需要的天数;每天加工的零件数和需要的天数乘积;反
表中每天加工的零件数和需要的天数是相关联的量,因为每天加工的零件数和需要的天数的乘积一定,所以这两个量成反比例。
故答案为:每天加工的零件数;需要的天数;每天加工的零件数和需要的天数乘积;反。
思路引导:表中每天加工的零件数随着需要的天数的增多而减少,所以每天加工的零件数和需要的天数是相关联的量,且120×2=240,80×3=240,60×4=240,48×5=240,40×6=240……,所以每天加工的零件数×需要的天数=总零件数(一定),乘积一定,因此这两个量成反比例。
12.
反;正
解:底×高=三角形面积×2(一定),三角形面积一定,它的底和高成反比例;
圆的周长÷半径=2(一定),圆的周长和半径成正比例。
故答案为:反;正。
思路引导:根据三角形面积公式和圆周长公式判断相关联的两个量的乘积一定还是商一定,如果乘积一定就成反比例,如果商一定就成正比例,否则不成比例。
13.
3;248;3
解:有图象可知:慢车比快车早出发3小时;快车追上慢车时行驶了248千米;
18-15=3(小时)
快车比慢车早3小时到达B地。
故答案为:3;248;3。
思路引导:所行的路程与时间的关系如图所示,横轴表示时间,纵轴表示路程,慢车从0时开始行驶,快车从3时开始行驶,所以慢车比快车早出发3小时;当快车和慢车行驶的路程相交时是248千米,所以快车追上慢车时行驶了248千米;快车15时到达,慢车18时到达,所以快车比慢车早3小时到达B地。
14.
4;1;正
解:x:y=4:1;x,y成正比例。
故答案为:4;1;正。
思路引导:=y,所以x=4y,所以x:y=4:1;
当xy=k(k为常数,x,y≠0)时,x和y成正比例关系。
15.
1600
解:设甲实际加工了x个零件,
[x÷(1+25%)]:(480÷60%)=8:5
??????????????????
?
?
?
?
?
x×5=800×8
???????????????????????
?
?
?
?
??
4x=6400
???????????????????????????
?
?
?
??
x=6400÷4
?????????????????????????????
?
??
?
x=1600
故答案为:1600
思路引导:设甲实际加工了x个零件,那么甲的任务就是x÷(1+25%),乙的任务是480÷60%,根据两人的任务比是8:5列出比例解答即可.
16.
150
解:设甲堆水泥原来有x袋.
0.2x×5=0.25(x-50)×6
x=1.5x-75
0.5x=75
x=150
故答案为:150
思路引导:设甲堆水泥原来有x袋,则乙堆水泥有(x-50)袋;甲剩下的水泥:(1-80%)x袋,乙剩下的水泥:(1-)(x-50)袋,根据甲、乙两堆剩下的水泥袋数的比是6:5列出比例解答即可.
17.
12
解:当重量是0千克时,弹簧的长度是12厘米,所以弹簧自身的长度就是12厘米.
故答案为:12
思路引导:横轴表示重量,纵轴表示弹簧长度,判断出重量为0时弹簧的长度就是弹簧自身的长度.
18.
30
因为总本书一定,则人数与每人分得的本数成反比例,
20×女=12×总,
女=总。
设总人数为5份,则女生为3份,男生为2份。
设男生平均每人可分得x本,可得:
x×2份=20×3份
?
?
?
?
?x=30
所以只发给男生,平均每人可分得30本。
故答案为:30.
思路引导:作业本总数一定,20×女生数=12×总人数,男生数×男生平均每人本数=女生数×20。
四、综合提升
19.
(1)路程;时间;正
(2)每行站的人数;站的行数;反
解:(1)路程÷时间=速度(一定);题目中,路程和时间成正比例关系;
(2)每行站的人数×站的行数=学生总人数(一定);每行站的人数和站的行数成反比例关系。
故答案为:(1)路程;时间;正;(2)每行站的人数;站的行数;反。
思路引导:(1)正比例的判断方法:相关联,能变化,商一定;
(2)反比例的判断方法:相关联,能变化,积一定。
20.
(1)正(2)16(3)200
解:(1)从图象中可以看出这辆汽车行驶的路程和时间成正比例;
(2)100÷2=50千米,800÷50=16小时,所以这辆汽车行800千米要16小时;
(3)100÷2=50千米,50×4=200千米,所以这辆汽车4小时能行200千米。
思路引导:(1)从图中看出,图像是从0开始呈直线上升,所以这辆汽车行驶的路程和时间成正比例关系;
(2)这辆汽车的速度=这辆汽车2小时行驶的距离÷2,那么这辆汽车行800千米要的时间=800÷速度;
(3)这辆汽车4小时能行驶的距离=速度×4。
21.
(1)正
(2)解:(50÷5﹣40÷5)÷(40÷5);
=2÷8,
=25%;
答:加工小齿轮的效率比大齿轮高25%
(3)解:①每人每天加工小齿轮的个数如下:50÷5=10(个),②每人每天加工大齿轮的个数如下:40÷5=8(个),③设加工小齿轮的人数是x人,则加工大齿轮的人数为(85﹣x).8×(85﹣x)=10×x÷3,
680﹣8x=
,680﹣8x+8x=
+8x,
+
=680,
=680,
×
=680×
,
x=60;加工大齿轮的人数是:85﹣x=85﹣60=25(人);答:加工大齿轮的人数是25人,加工小齿轮的人数是60人.
解:(1)据图象判断,加工齿轮的个数和天数成正比例.
思路引导:(1)根据图象判断,加工齿轮的个数随着加工的时间增加而增多.(2)相同的时间内,加工小齿轮的个数比大齿轮多的是大齿轮百分之几.(3)先求出每个工人每天加工大齿轮、小齿轮各加工几个,再设出加工大、小齿轮的人数,然后在运用方程解答.本题借助折线统计图考查了学生两个量成比例问题,一个数比另一个数多百分之几的问题,同时考查了工作量与人数分配问题.只要认真思考,就能正确的解答.
五、解答问题
22.
(1)反
(2)解:设需要多x个小正方形.
???????
36x=216×4
36x÷36=216×4÷36
?????????
x=24
答:需要24个小正方形。
思路引导:(1)经过计算,每个小正方形的面积×所需小正方形的数量是一个定值,所以每个小正方形的面积与所需小正方形的数量成反比例关系;
(2)本题可以设需要x个小正方形,题中存在的比例关系是:36×需要面积是36cm2的小正方形的个数=4×需要面积是4cm2的小正方形的个数,据此代入数据和字母作答即可。
23.
解:设还要加工x小时才能完成任务。
????????????
78(6+x)=221×6
??
468+78x=1326
???????????
78x=1326-468
???????????
78x=858
???????????????
x=858÷78
???????????????
x=11
答:还要加工11小时才能完成任务。
思路引导:工作总量÷工作时间=工效(一定),列出正比例,解比例。
24.
(1)解:设需要用x升油。
8:100=x:80
???
100x=8×80
??
100x=640
????????
x=640÷100
????????
x=6.4
答:需要用6.4升油。
(2)解:设甲地与乙地相距x千米。
100:8=x:6.4
?????
?
8x=100×6.4
???????
8x=640
?????????
x=640÷8
?????????
x=80
答:甲地与乙地相距80千米。
思路引导:(1)8升油:百千米=需要油的升数:行驶的路程;
(2)百千米路程:8升=甲地与乙地距离:共耗油升数。
25.
解:设每人要栽x棵。
(40+10)x=40×15
?
?
?
?
?
?
?50x=600
?
?
?
?
?
?
?
?
?x=600÷50
?
?
?
?
?
?
?
?
?x=12
答:每人要栽12棵。
思路引导:每人栽的棵数×人数=总棵数,每人栽的棵数与人数成反比例,设出未知数,根据总棵数不变列出比例,解比例求出每人要栽的棵数。
26.
解:设需要x块。
602x=302×600
x=150
解:设需要x块。
60?x=30?×600
360x=540000
?
?
?
x=540000÷360
?
?
?
x=150
答:需要150块。
思路引导:每块的面积×块数=图书室总面积,总面积不变,每块面积与块数成反比例,设出未知数,根据总面积不变列出比例解答即可。
27.
解:8×45÷[8×(1-10%)]
=360÷[8×0.9]
=360÷7.2
=50(天)
50-45=5(天)
答:这样可以多烧5天?。
思路引导:煤总数=计划每天烧的数量×计划天数,实际每天烧的数量=计划每天烧的数量×(1-10%)
实际天数=煤总数÷实际每天烧的数量,多烧天数=实际天数-计划天数。
28.
(1)
时间/小时
3
4
路程/千米
600?
?
?
??
800?
?
?
?
(2)正(3)9
(2)路程÷时间=200(一定),行驶的时间和路程成正比例;
(3)1800÷200=9(小时)。
故答案为:(2)正;(3)9。
思路引导:(1)图中横轴表示时间,竖轴表示路程,根据图形直接判断3小时行驶的路程,800千米需要的时间;
(2)根据时间和路程相对应的数据确定路程和时间的比值一定,二者就成正比例关系;
(3)用路程除以速度即可求出行驶的时间。
知识互联网
知识导航
夯实基础
能力提升
能力达标百分训练(答案解析)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
