4.3平行线的性质的说课(北师大)

(共18张PPT)
教学内容
平行线的性质
平行线的性质
平行线的性质
教学目标
2、能力目标：通过本节课的教学，培养学生的概括能力和“观察－猜想－证明”的科学探索方法，培养学生的辩证思维能力和逻辑思维能力．
3、情感目标：培养学生的主体意识，向学生渗透讨论的数学思想，培养学生思维的灵活性和广阔性．
1、知识目标：使学生理解平行线的性质，能初步运用平行线的性质进行有关计算．
教学难点：正确区分平行线的性质和判定　　　　　是本节课的难点．
教学重点：平行线性质的研究和发现过程　　　　　是本节课的重点．
教学方法：开放式
教学过程
1、问题引入
请同学们先复习一下前面所学过的平行线的判 定方法，并说出它们的已知和结论分别是什么？
想一想：若交换它们的已知和结论，即让两直线平行，会有什么结论呢？
平行线的判定
两条直线被第三条直线所截，
⑴若同位角相等，则两直线平行；
⑵若内错角相等，则两直线平行；
⑶若同旁内角互补，则两直线平行．
带着这个问题，我们来看……
已知
结论
已知
结论
已知
结论
A
B
C
D
E
F
1
2
4
3
8
5
6
7
图1
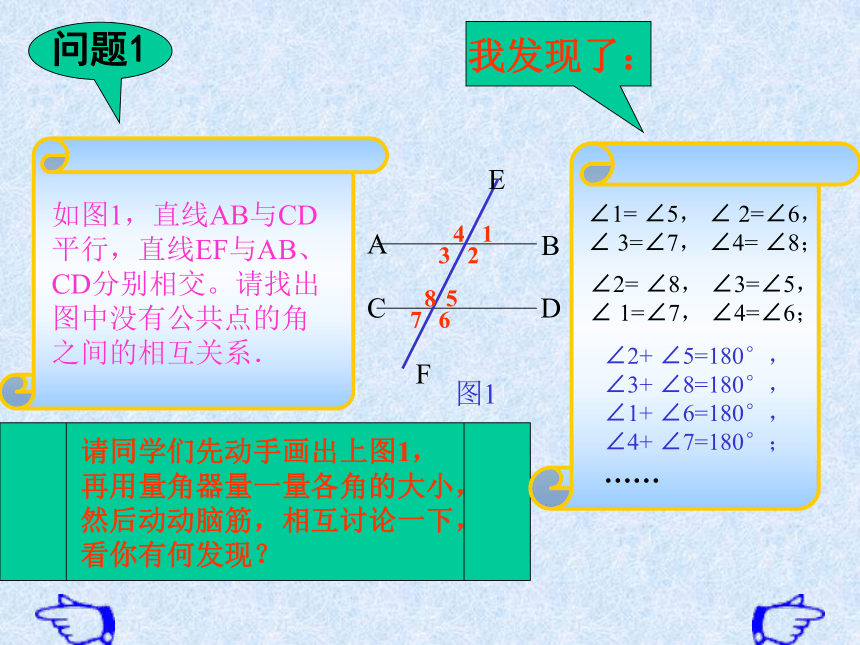
问题1
如图1，直线AB与CD平行，直线EF与AB、CD分别相交。请找出图中没有公共点的角之间的相互关系．
请同学们先动手画出上图1，再用量角器量一量各角的大小，然后动动脑筋，相互讨论一下，看你有何发现？
我发现了：
∠1= ∠5， ∠ 2=∠6，
∠ 3=∠7， ∠4= ∠8；
∠2+ ∠5=180°，
∠3+ ∠8=180°，
∠1+ ∠6=180°，
∠4+ ∠7=180°；
……
∠2= ∠8， ∠3=∠5，
∠ 1=∠7， ∠4=∠6；
问题2
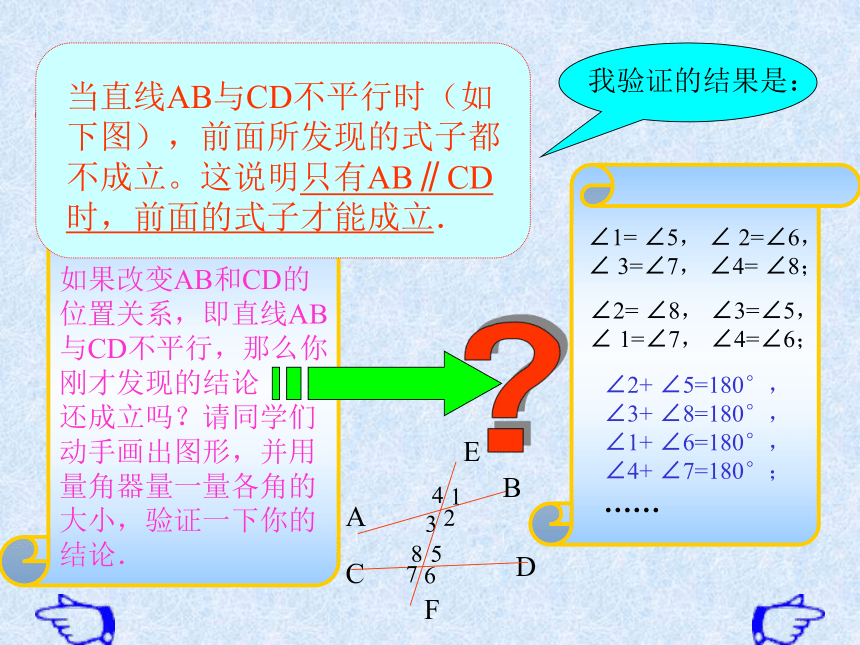
如果改变AB和CD的位置关系，即直线AB与CD不平行，那么你刚才发现的结论
还成立吗？请同学们动手画出图形，并用量角器量一量各角的大小，验证一下你的结论．
2、问题探索
我验证的结果是：
∠1= ∠5， ∠ 2=∠6，
∠ 3=∠7， ∠4= ∠8；
∠2+ ∠5=180°，
∠3+ ∠8=180°，
∠1+ ∠6=180°，
∠4+ ∠7=180°；
……
∠2= ∠8， ∠3=∠5，
∠ 1=∠7， ∠4=∠6；
当直线AB与CD不平行时（如下图），前面所发现的式子都不成立。这说明只有AB∥CD时，前面的式子才能成立．
D
5
A
C
E
F
3
B
1
2
4
6
7
8
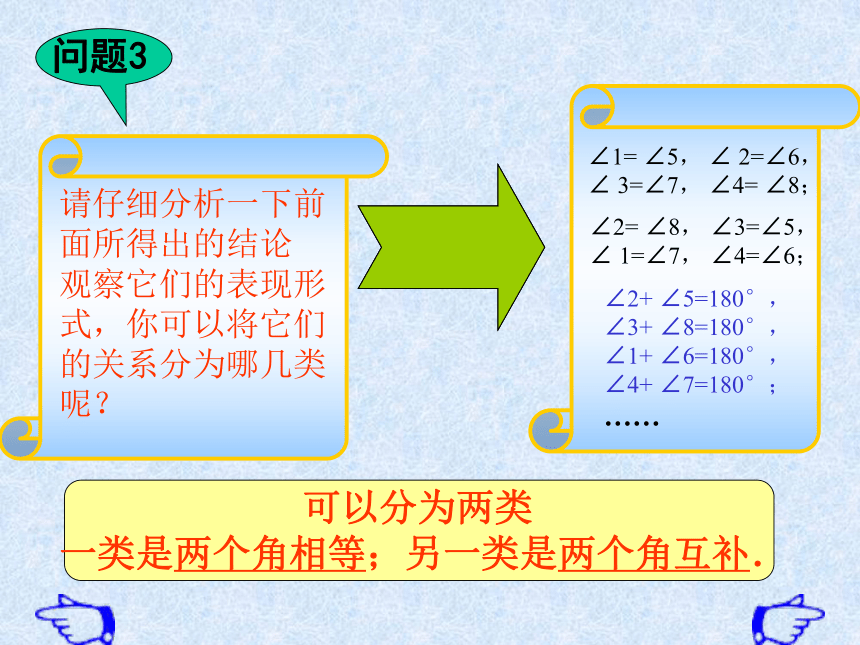
问题3
请仔细分析一下前面所得出的结论
观察它们的表现形式，你可以将它们的关系分为哪几类呢？
可以分为两类
一类是两个角相等；另一类是两个角互补．
∠1= ∠5， ∠ 2=∠6，
∠ 3=∠7， ∠4= ∠8；
∠2+ ∠5=180°，
∠3+ ∠8=180°，
∠1+ ∠6=180°，
∠4+ ∠7=180°；
……
∠2= ∠8， ∠3=∠5，
∠ 1=∠7， ∠4=∠6；
∠1= ∠5， ∠ 2=∠6，
∠ 3=∠7， ∠4= ∠8；
∠2+ ∠5=180°，
∠3+ ∠8=180°，
∠1+ ∠6=180°，
∠4+ ∠7=180°；
……
∠2= ∠8， ∠3=∠5，
∠ 1=∠7， ∠4=∠6；
问题4
（1）具有相等关系的两角有怎样的位置关系呢？（请甲组同学回答）
（2）互补的两角又有怎样的位置关系呢？（请乙组同学回答）
（2）具有互补关系的两个角，有的是同旁内角，如∠2与 ∠5等都是同旁内角； 还有一些说不出名字的角，如 ∠1与 ∠6等，书上没有定义．
E
F
A
B
C
D
1
2
4
3
8
5
6
7
（1）具有相等关系的两个角，有的是同位角，有的是内错角，如∠1与 ∠5等都是同位角； ∠2与 ∠8等都是内错角。还有一些说不出名字的角，如 ∠1与 ∠7， ∠4与∠6等．
问题5
不考虑没有定义的角的位置关系，只对同位角、内错角、同旁内角进行归纳总结，若两条平行线被第三条直线所截，你可以得出哪些结论？
若两条平行线被第三条直线所截，则 （1）同位角相等，
（2）内错角相等，
（3）同旁内角互补。
简单地说，就是：
　　两直线平行，
（1）同位角相等，
（2）内错角相等，
（3）同旁内角互补．
这就是本节课我们所要研究的课题　　　－－平行线的性质
3、归纳小结
平行线的性质
（1）两条平行线被第三条直线所截，同位角相等；
（2）两条平行线被第三条直线所截，内错角相等；
（3）两条平行线被第三条直线所截，同旁内角互补。
（1）两直线平行，同位角相等；
简单地说，就是：
（2）两直线平行，内错角相等；
（3）两直线平行，同旁内角互补。
从平行线的作法中，我们已经知道公理：同位角相等，两直线平行。现在我们将它作为扩大了的公理得：两条平行线被第三条直线所截，同位角相等，简单地说，就是：
两直线平行，同位角相等．
下面以此为基础，我们来证明：
1.两直线平行，内错角相等；
2.两直线平行，同旁内角互补．
（由甲组同学讨论解决）
（由乙组同学讨论解决）
学生甲组：
∵AB ∥ CD（已知）
∴ ∠1＝∠5（两直线平行，同位角相等）
又∵∠1＝∠3（对顶角相等）
∴∠3＝∠5（等量代换）
学生乙组：
∵AB ∥ CD（已知）
∴ ∠1＝∠5（两直线平行，同位角相等）
又∵∠1＋∠2＝180°（邻补角的定义）
∴∠2＋∠5＝ 180° （等量代换）
E
F
A
B
C
D
1
2
4
3
8
5
6
7
练习1：
如图，已知两平行线AB、CD被直线AE所截。
（1）从∠1＝110 °可以知道∠2是多少度？为什么？
（2）从∠1＝110 °可以知道∠3是多少度？为什么？
（3）从∠1＝110 °可以知道∠4是多少度？为什么？
解：∠3＝110°
∵AB∥CD（已知）
∴∠1＝∠3（两直线平行，同位角相等）
又∵ ∠1＝110°（已知）
∴∠3＝110°（等量代换）
4、练习
A
B
D
C
E
2
4
3
1
解：∠4＝70°
∵AB∥CD（已知）
∴∠1＋∠4＝180°（两直线平行，同旁内角互补）
又∵ ∠1＝110°（已知）
∴∠4＝70°
请同学们注意：解题中可别把平行线的判定和性质搞混了。由角的已知条件推出两线平行的结论是平行线的判定；而由两线的平行条件推出角的结论则是平行线的性质。
解：∠2＝110°
∵AB∥CD（已知）
∴∠1＝∠2（两直线平行，内错角相等）
又∵ ∠1＝110°（已知）
∴∠2＝110°（等量代换）
练习2：
根据右边的图形，在括号内填上相应的理由：
①∵∠1＝∠C（　　　　）
　∴AB∥CD（　　　　　　　　　　　　　　）
② ∵∠1＝∠B（　　　　）
　∴EC∥BD（　　　　　　　　　　　　　　）
③ ∵∠2＋∠B＝180°（　　　　）
　∴EC∥BD（　　　　　　　　　　　　　　）
④ ∵AB∥CD（　　　　　）
　 ∴ ∠3＝∠C（　　　　　　　　　　　　　）
⑤ ∵EC∥BD（　　　　　）
　 ∴ ∠3＝∠B（　　　　　　　　　　　　　）
⑥ ∵AB∥CD（　　　　　）
　 ∴ ∠2＋∠C＝ 180° （　　　　　　　　　　　　）
E
A
C
D
B
1
2
3
4
同位角相等，两直线平行
两直线平行，内错角相等
已知
已知
已知
已知
已知
已知
内错角相等，两直线平行
同旁内角互补，两直线平行
两直线平行，同位角相等
两直线平行，同旁内角互补
说明：①、②、③是平行线的判定的应用；　　　④、⑤、⑥是平行线的性质的应用．
5、应用举例
如图是梯形有上底的一部分，已经量得∠A＝115°， ∠D＝100°，那么梯形的另外两个角各是多少度？
分析
解答
5、例题讲解
如图是梯形有上底的一部分，已经量得∠A＝115°， ∠D＝100°，那么梯形的另外两个角各是多少度？
分析
解答
　
　　因为梯形的上下两底是平行的，观察图形可知，AD∥BC，且∠B与已知的∠A是同旁内角，∠C与已知的∠D也是同旁内角，所以根据平行线的性质“两直线平行，同旁内角互补”可以建立∠B与∠A， ∠C与∠D之间的数量关系，从而使问题得解．
5、例题讲解
如图是梯形有上底的一部分，已经量得∠A＝115°， ∠D＝100°，那么梯形的另外两个角各是多少度？
分析
解答
解：
∵AD ∥BC（已知）
∴ ∠A＋∠B＝ 180° ，
　 ∠D＋∠C＝ 180° （两直线平行，同旁内角互补）
∴ ∠B＝180°－115°＝ 65°，
　∠C＝180°－ 100°＝ 80°。
故梯形的另外两个角分别是65°和80°．
6、课堂小结
E
F
A
B
C
D
1
2
4
3
8
5
6
7
本节课你学到了哪些知识？
（1）平行线的性质有哪三条？
（2）如何区分平行线的判定和性质？
平行线的性质有以下三条，
（1）两直线平行，同位角相等，
（2）两直线平行，内错角相等，
（3）两直线平行，同旁内角互补．
由角的已知条件推出两线的平行的结论是平行线的判定；而由两线的平行的条件推出角的结论则是平行线的性质．
谢 谢 光 临