新课标人教B版选修1-2综合测试(4)
文档属性
| 名称 | 新课标人教B版选修1-2综合测试(4) |

|
|
| 格式 | zip | ||
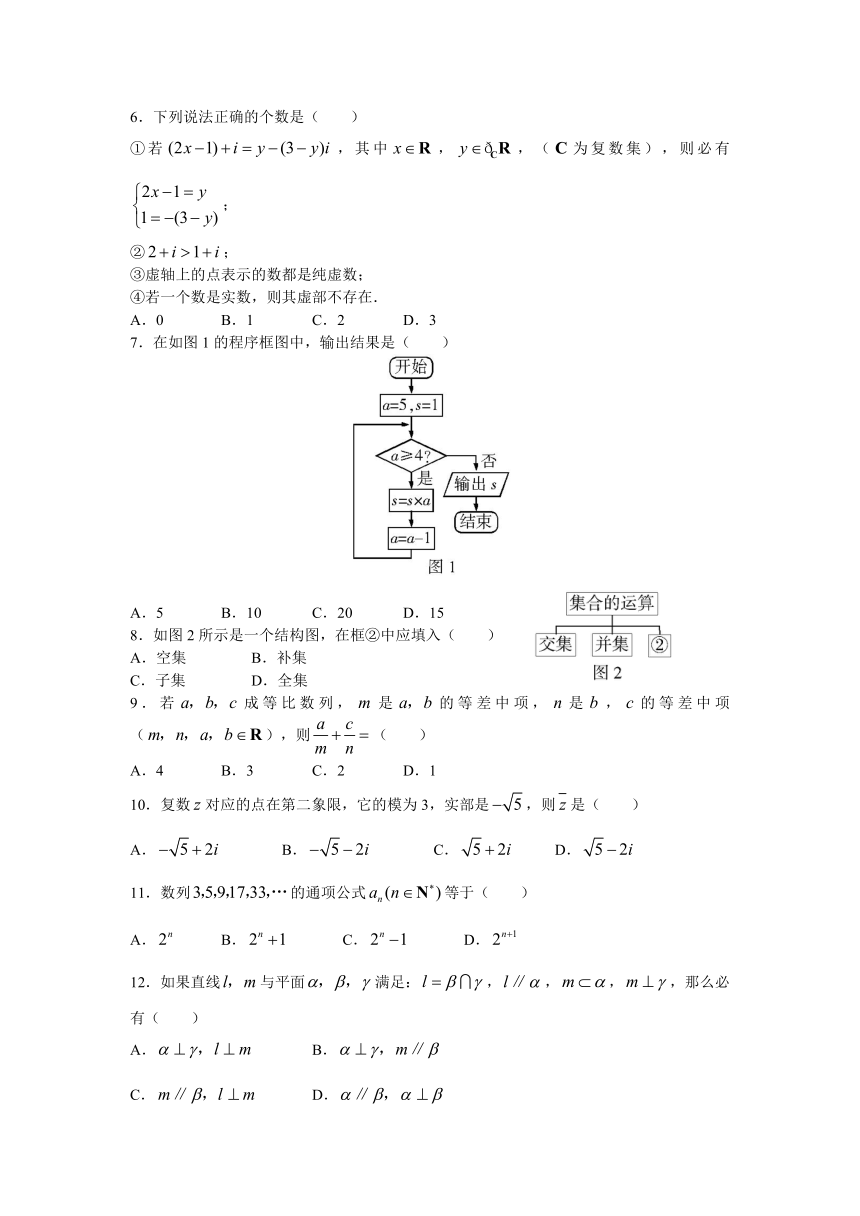
| 文件大小 | 141.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-22 00:00:00 | ||
图片预览


文档简介
新课标人教B版选修1-2综合测试(4)
一、选择题
1.由一组数据得到的回归直线方程为,则下列说法不正确的是( )
A.直线必过点
B.直线至少经过点中的一个点
C.直线的斜率为
D.设随机误差,(),我们用全部误差的平方和的大小来度量总的误差大小
2.下面几种推理过程是演绎推理的是( )
A.两条直线平行,同旁内角互补,如果和是两条平行直线的同旁内角,则
B.由平面三角形的性质,推测空间四面体的性质
C.三角形内角和是,四边形内角和是,五边形内角和是,由此得凸多边形内角和是
D.在数列中,,,由此归纳出的通项公式
3.复数的共轭复数是( )
A. B. C. D.
4.数列前100项的和等于( )
A. B. C. D.
5.在一次实验中,测得的四组值分别是,则与之间的回归直线方程为( )
A. B. C. D.
6.下列说法正确的个数是( )
①若,其中,,(为复数集),则必有;
②;
③虚轴上的点表示的数都是纯虚数;
④若一个数是实数,则其虚部不存在.
A.0 B.1 C.2 D.3
7.在如图1的程序框图中,输出结果是( )
A.5 B.10 C.20 D.15
8.如图2所示是一个结构图,在框②中应填入( )
A.空集 B.补集
C.子集 D.全集
9.若成等比数列,是的等差中项,是,的等差中项(),则( )
A.4 B.3 C.2 D.1
10.复数对应的点在第二象限,它的模为3,实部是,则是( )
A. B. C. D.
11.数列的通项公式等于( )
A. B. C. D.
12.如果直线与平面满足:,,,,那么必有( )
A. B.
C. D.
二、填空题
13.反证法的证明过程可以概括为“否定—推理—否定”,即从否定结论开始,经过正确的推理,导致逻辑矛盾,从而达到新的否定(即肯定原命题)的过程.用反证法证明命题“若则”的过程可用框图表示为 .
14.已知函数,那么
.
15.试求的值,由此推测时, ,
, , , .
16.某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个一天卖出的热饮杯数与当天气温的对比表:
摄氏温度(℃) 0 4 7 12 15 19 23 27 31 36
热饮杯数 156 150 132 128 130 116 104 89 93 76 54
如果某天气温是℃.预测这天卖出的热饮杯数为 .
三、解答题
17.已知复数.当实数取什么值时,复数是:
(1)零;
(2)虚数;
(3)纯虚数;
(4)复平面内第二、四象限角平分线上的点对应的复数.
18.已知数列的前项和为,,满足,计算,并猜想的表达式.
19.如图3,是所在平面外一点,,平面,是的中点,是上的点,.求证:.
20.某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人;不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人.则认为“喜欢玩电脑游戏与认为作业量的多少有关系”的把握大约是多少?
21.阅读下面文字,然后根据获取的信息画出树形结构图.
1890年,英国物理学家J.J.汤姆生对阴极射线进行了一系列实验研究.直到1897年,他在根据阴极射线在电场和磁场中偏转断定它的本质是带负电的粒子流,这粒子流的组成成份就是后来我们所知道的电子,随着对电子的认识,他提出了一种正负电荷在原子内的存在模型——枣糕模型.但在1909年,英籍物理学家卢瑟福用粒子散射实验,推翻了汤姆生先生最初的“枣糕模型”,从而确定了卢瑟福的核式结构模型.随着科技的发展,人们又知道质子与中子组成了原子核,原子核间的作用力可以放出巨大的能量,这就是我们所熟悉的核能.随着我们学习知识的增长,微观世界的更多奥秘正等待我们去探索、去发现.
参考答案
一、选择题
1.B
2.A
3.B
4.A
5.A
6.A
7.C
8.B
9.C
10.B
11.B
12.A
二、填空题
13.肯定条件,否定结论导出逻辑矛盾“若则”为假“若则”为真
14. 3.5
15.
16. 101
三、解答题
17.解:由于,复数可以表示为
.
(1)当即时,为零;
(2)当,即且时,为虚数;
(3)当即时,为纯虚数;
(4)当时,即或时,为复平面内第二、四象限角平分线上的点对应的复数.
18.解:,,即,
解得,
同理可解得,,
可猜想.
19.证明:取的中点,连结,
是的中点,
,
平面,平面,
,取的中点,连结,
则,
,,
又,,,
平面,.
20.解:
认为作业多 认为作业不多 总数
喜欢玩电脑游戏 18 9 27
不喜欢玩电脑游戏 8 15 23
总数 26 24 50
,
有的把握认为“喜欢玩电脑游戏与认为作业量的多少”有关系.
21.解:
一、选择题
1.由一组数据得到的回归直线方程为,则下列说法不正确的是( )
A.直线必过点
B.直线至少经过点中的一个点
C.直线的斜率为
D.设随机误差,(),我们用全部误差的平方和的大小来度量总的误差大小
2.下面几种推理过程是演绎推理的是( )
A.两条直线平行,同旁内角互补,如果和是两条平行直线的同旁内角,则
B.由平面三角形的性质,推测空间四面体的性质
C.三角形内角和是,四边形内角和是,五边形内角和是,由此得凸多边形内角和是
D.在数列中,,,由此归纳出的通项公式
3.复数的共轭复数是( )
A. B. C. D.
4.数列前100项的和等于( )
A. B. C. D.
5.在一次实验中,测得的四组值分别是,则与之间的回归直线方程为( )
A. B. C. D.
6.下列说法正确的个数是( )
①若,其中,,(为复数集),则必有;
②;
③虚轴上的点表示的数都是纯虚数;
④若一个数是实数,则其虚部不存在.
A.0 B.1 C.2 D.3
7.在如图1的程序框图中,输出结果是( )
A.5 B.10 C.20 D.15
8.如图2所示是一个结构图,在框②中应填入( )
A.空集 B.补集
C.子集 D.全集
9.若成等比数列,是的等差中项,是,的等差中项(),则( )
A.4 B.3 C.2 D.1
10.复数对应的点在第二象限,它的模为3,实部是,则是( )
A. B. C. D.
11.数列的通项公式等于( )
A. B. C. D.
12.如果直线与平面满足:,,,,那么必有( )
A. B.
C. D.
二、填空题
13.反证法的证明过程可以概括为“否定—推理—否定”,即从否定结论开始,经过正确的推理,导致逻辑矛盾,从而达到新的否定(即肯定原命题)的过程.用反证法证明命题“若则”的过程可用框图表示为 .
14.已知函数,那么
.
15.试求的值,由此推测时, ,
, , , .
16.某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个一天卖出的热饮杯数与当天气温的对比表:
摄氏温度(℃) 0 4 7 12 15 19 23 27 31 36
热饮杯数 156 150 132 128 130 116 104 89 93 76 54
如果某天气温是℃.预测这天卖出的热饮杯数为 .
三、解答题
17.已知复数.当实数取什么值时,复数是:
(1)零;
(2)虚数;
(3)纯虚数;
(4)复平面内第二、四象限角平分线上的点对应的复数.
18.已知数列的前项和为,,满足,计算,并猜想的表达式.
19.如图3,是所在平面外一点,,平面,是的中点,是上的点,.求证:.
20.某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人;不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人.则认为“喜欢玩电脑游戏与认为作业量的多少有关系”的把握大约是多少?
21.阅读下面文字,然后根据获取的信息画出树形结构图.
1890年,英国物理学家J.J.汤姆生对阴极射线进行了一系列实验研究.直到1897年,他在根据阴极射线在电场和磁场中偏转断定它的本质是带负电的粒子流,这粒子流的组成成份就是后来我们所知道的电子,随着对电子的认识,他提出了一种正负电荷在原子内的存在模型——枣糕模型.但在1909年,英籍物理学家卢瑟福用粒子散射实验,推翻了汤姆生先生最初的“枣糕模型”,从而确定了卢瑟福的核式结构模型.随着科技的发展,人们又知道质子与中子组成了原子核,原子核间的作用力可以放出巨大的能量,这就是我们所熟悉的核能.随着我们学习知识的增长,微观世界的更多奥秘正等待我们去探索、去发现.
参考答案
一、选择题
1.B
2.A
3.B
4.A
5.A
6.A
7.C
8.B
9.C
10.B
11.B
12.A
二、填空题
13.肯定条件,否定结论导出逻辑矛盾“若则”为假“若则”为真
14. 3.5
15.
16. 101
三、解答题
17.解:由于,复数可以表示为
.
(1)当即时,为零;
(2)当,即且时,为虚数;
(3)当即时,为纯虚数;
(4)当时,即或时,为复平面内第二、四象限角平分线上的点对应的复数.
18.解:,,即,
解得,
同理可解得,,
可猜想.
19.证明:取的中点,连结,
是的中点,
,
平面,平面,
,取的中点,连结,
则,
,,
又,,,
平面,.
20.解:
认为作业多 认为作业不多 总数
喜欢玩电脑游戏 18 9 27
不喜欢玩电脑游戏 8 15 23
总数 26 24 50
,
有的把握认为“喜欢玩电脑游戏与认为作业量的多少”有关系.
21.解:
