2020-2021学年高中人教A版数学必修3学案 2.3.1 变量之间的相关关系 2.3.2 两个变量的线性相关 Word版含解析
文档属性
| 名称 | 2020-2021学年高中人教A版数学必修3学案 2.3.1 变量之间的相关关系 2.3.2 两个变量的线性相关 Word版含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 480.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 00:00:00 | ||
图片预览



文档简介
2.3 变量间的相关关系
2.3.1 变量之间的相关关系
2.3.2 两个变量的线性相关
学 习 目 标 核 心 素 养
1.了解变量间的相关关系,会画散点图,并利用散点图判断两个变量之间是否具有相关关系.(重点) 2.了解线性回归思想,会求回归直线方程.(难点) 1.通过对数据的分析、统计,培养数据分析素养.
2.借助变量间相关关系的研究,提升数学运算素养.
1.变量间的相关关系
(1)相关关系的定义
变量间确实存在关系,但又不具备函数关系所要求的确定性,它们的关系是带有不确定性的,那么这两个变量之间的关系叫做相关关系,两个变量之间的关系分为函数关系和相关关系.
(2)散点图
将样本中n个数据点(xi,yi)(i=1,2,…,n)描在平面直角坐标系中得到的图形叫做散点图.
(3)正相关与负相关
①正相关:如果一个变量的值由小变大时,另一个变量的值也由小变大,这种相关称为正相关.
②负相关:如果一个变量的值由小变大时,另一个变量的值由大变小,这种相关称为负相关.
2.回归直线方程
(1)回归直线:如果散点图中点的分布从整体上看大致在一条直线附近,就称这两个变量之间具有线性相关关系,这条直线叫做回归直线.
(2)线性回归方程:回归直线对应的方程叫做回归直线的方程,简称回归方程.
(3)最小二乘法:
求线性回归方程=x+时,使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法.
其中,是线性回归方程的斜率,是线性回归方程在y轴上的截距.
1.下列两个变量具有相关关系的是( )
A.角度和它的余弦值
B.圆的半径和该圆的面积
C.正n边形的边数和它的内角和
D.居民的收入与存款
D [A、B、C中两变量是确定的函数关系.]
2.某工厂某产品产量x(千件)与单位成本y(元)满足回归直线方程=77.36-1.82x,则以下说法中正确的是( )
A.产量每增加1 000件,单位成本约下降1.82元
B.产量每减少1 000件,单位成本约下降1.82元
C.当产量为1千件时,单位成本为75.54元
D.当产量为2千件时,单位成本为73.72元
A [令f(x)=77.36-1.82x,因为f(x+1)-f(x)=77.36-1.82(x+1)-77.36+1.82x=-1.82,所以产量每增加1 000件,单位成本约下降1.82元.]
3.5位学生的数学成绩和物理成绩如下表:
学科 A B C D E
数学 80 75 70 65 60
物理 70 66 68 64 62
则数学成绩与物理成绩之间( )
A.是函数关系
B.是相关关系,但相关性很弱
C.具有较好的相关关系,且是正相关
D.具有较好的相关关系,且是负相关
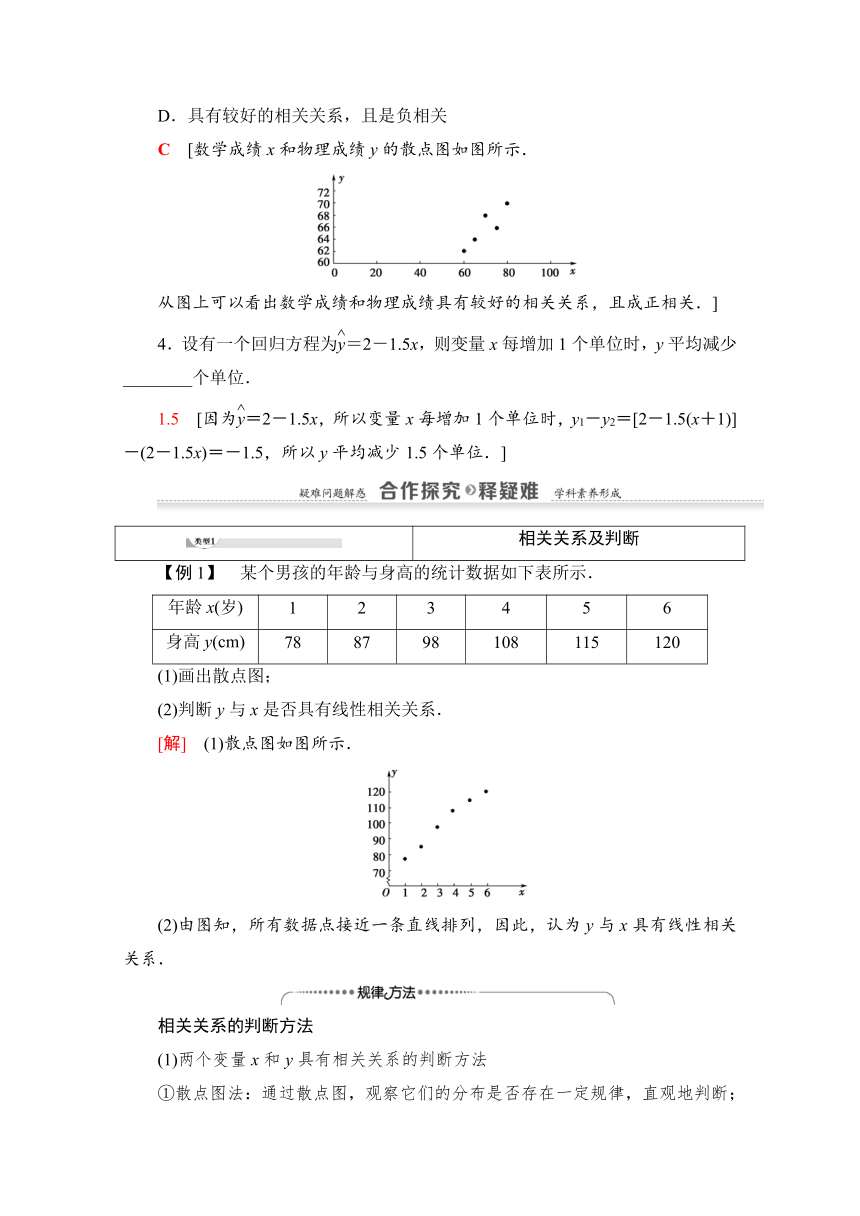
C [数学成绩x和物理成绩y的散点图如图所示.
从图上可以看出数学成绩和物理成绩具有较好的相关关系,且成正相关.]
4.设有一个回归方程为=2-1.5x,则变量x每增加1个单位时,y平均减少________个单位.
1.5 [因为=2-1.5x,所以变量x每增加1个单位时,y1-y2=[2-1.5(x+1)]-(2-1.5x)=-1.5,所以y平均减少1.5个单位.]
相关关系及判断
【例1】 某个男孩的年龄与身高的统计数据如下表所示.
年龄x(岁) 1 2 3 4 5 6
身高y(cm) 78 87 98 108 115 120
(1)画出散点图;
(2)判断y与x是否具有线性相关关系.
[解] (1)散点图如图所示.
(2)由图知,所有数据点接近一条直线排列,因此,认为y与x具有线性相关关系.
相关关系的判断方法
(1)两个变量x和y具有相关关系的判断方法
①散点图法:通过散点图,观察它们的分布是否存在一定规律,直观地判断;
②表格、关系式法:结合表格或关系式进行判断;
③经验法:借助积累的经验进行分析判断.
(2)判断两个变量x和y之间是否具有线性相关关系,常用的简便方法就是绘制散点图,如果发现点的分布从整体上看大致在一条直线附近,那么这两个变量就是线性相关的,注意不要受个别点的位置的影响.
1.下列关系中,属于相关关系的是________(填序号).
①正方形的边长与面积之间的关系;
②农作物的产量与施肥量之间的关系;
③出租车费与行驶的里程;
④降雪量与交通事故的发生率之间的关系.
②④ [在①中,正方形的边长与面积之间的关系是函数关系;在②中,农作物的产量与施肥量之间不具有严格的函数关系,但具有相关关系;③为确定的函数关系;在④中,降雪量与交通事故的发生率之间具有相关关系.]
求回归方程
[探究问题]
1.任意两个统计数据是否均可以作出散点图?
[提示] 任意两个统计数据均可以作出散点图.
2.任何一组数据都可以由最小二乘法得出回归方程吗?
[提示] 用最小二乘法求回归方程的前提是先判断所给数据具有线性相关关系,否则求回归方程是无意义的.
3.回归系数的含义是什么?
[提示] (1) 代表x每增加一个单位,y的平均增加单位数,而不是增加单位数.
(2)当>0时,两个变量呈正相关关系,含义为:x每增加一个单位,y平均增加个单位数;
当<0时,两个变量呈负相关关系,含义为:x每增加一个单位,y平均减少个单位数.
【例2】 一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,收集数据如下:
零件数x(个) 10 20 30 40 50 60 70 80 90 100
加工时间y(分) 62 68 75 81 89 95 102 108 115 122
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求y关于x的回归直线方程.
思路点拨:画散点图→确定相关关系→求回归直线系数→写回归直线方程.
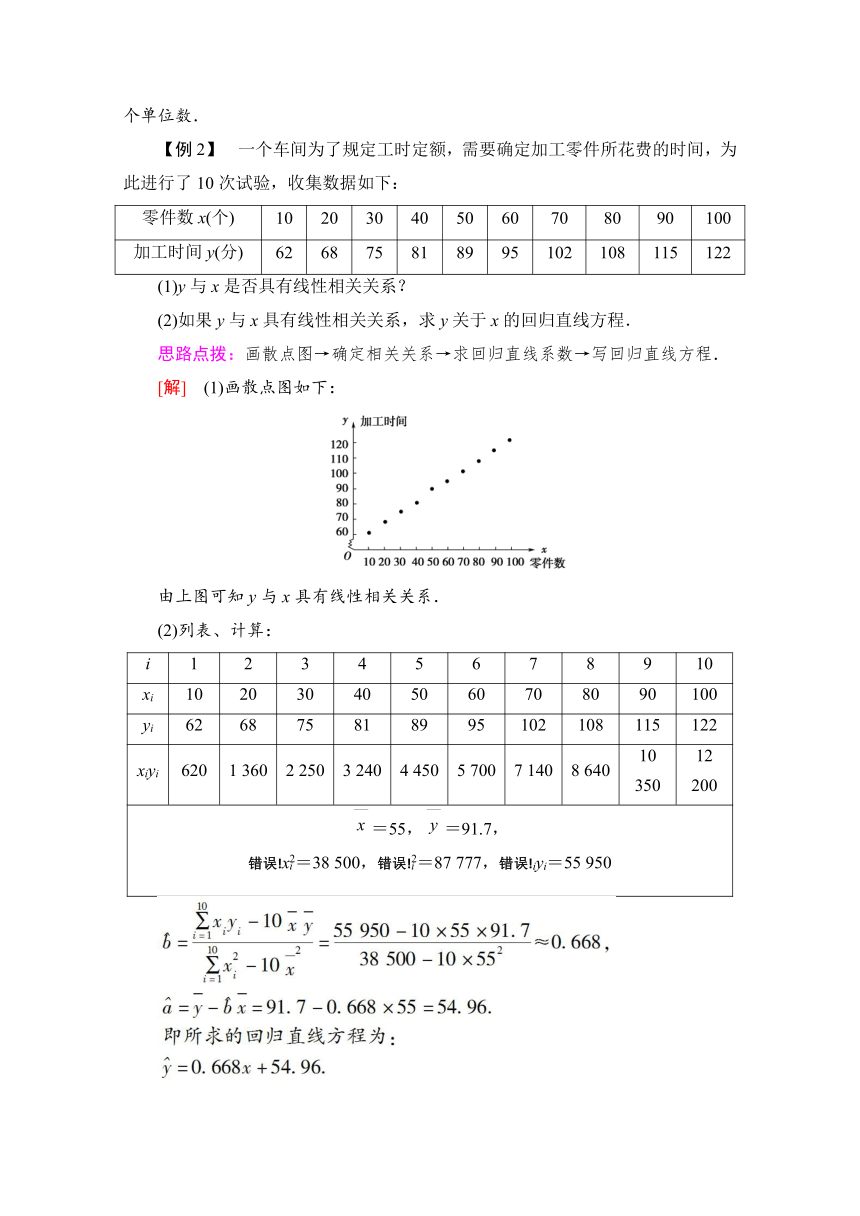
[解] (1)画散点图如下:
由上图可知y与x具有线性相关关系.
(2)列表、计算:
i 1 2 3 4 5 6 7 8 9 10
xi 10 20 30 40 50 60 70 80 90 100
yi 62 68 75 81 89 95 102 108 115 122
xiyi 620 1 360 2 250 3 240 4 450 5 700 7 140 8 640 10 350 12 200
=55,=91.7, x=38 500,=87 777,iyi=55 950
求回归直线方程的步骤
(1)收集样本数据,设为(xi,yi)(i=1,2,…,n)(数据一般由题目给出).
(2)作出散点图,确定x,y具有线性相关关系.
2.某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x 2 4 5 6 8
y 30 40 60 50 70
(1)画出散点图;
(2)求回归方程.
[解] (1)散点图如图所示.
(2)列出下表,并用科学计算器进行有关计算.
i 1 2 3 4 5
xi 2 4 5 6 8
yi 30 40 60 50 70
xiyi 60 160 300 300 560
x 4 16 25 36 64
=5,=50,=145,iyi=1 380
于是可得,===6.5,
=-=50-6.5×5=17.5.
于是所求的回归方程是=6.5x+17.5.
回归方程的应用
【例3】 为了解某地区某种农产品的年产量x(单位:吨)对价格y(单位:千元/吨)的影响,对近五年该农产品的年产量和价格统计如表:
x 1 2 3 4 5
y 8 6 5 4 2
已知x和y具有线性相关关系.
(1)求,;
(2)求y关于x的线性回归方程=x+;
(3)若年产量为4.5吨,试预测该农产品的价格.
[解] (1)计算可得==3,==5.
因为线性回归直线过(,),则=-=5-(-1.4×3)=9.2,
故y关于x的线性回归方程是=-1.4x+9.2.
(3)当x=4.5时,=-1.4×4.5+9.2=2.9(千元/吨).
利用线性回归方程解题的常见思路及注意点
(1)利用回归直线过样本点的中心,可以求参数问题,参数可涉及回归方程或样本点数据.
(2)利用回归方程中系数的意义,分析实际问题.
(3)利用回归直线进行预测,此时需关注两点;①所得的值只是一个估计值,不是精确值;②变量x与y成线性相关关系时,线性回归方程才有意义,否则即使求出线性回归方程也是毫无意义的,用其估计和预测的量也是不可信的.
3.平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第90条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以100元罚款,记3分的行政处罚.如表是本市一主干路段监控设备所抓拍的5个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份 1 2 3 4 5
违章驾驶员人数 120 105 100 90 85
(1)请利用所给数据求违章人数y与月份x之间的回归直线方程=x+;
(2)预测该路段7月份的不“礼让斑马线”违章驾驶员人数.
[解] (1)由表中数据得,=×(1+2+3+4+5)=3,
=×(120+105+100+90+85)=100,
==
=
=-8.5,
=-b=100+8.5×3=125.5.
所以y与x之间的回归直线方程为y=-8.5x+125.5.
(2)x=7时,y=-8.5x+125.5=66,
预测该路段7月份的不“礼让斑马线”违章驾驶员人数为66人.
1.判断变量之间有无相关关系,简便可行的方法就是绘制散点图.根据散点图,可看出两个变量是否具有相关关系,是否线性相关,是正相关还是负相关.
2.求回归直线的方程时应注意的问题
(1)知道x与y呈线性相关关系,无需进行相关性检验,否则应首先进行相关性检验.如果两个变量之间本身不具有相关关系,或者说,它们之间的相关关系不显著,即使求出回归方程也是毫无意义的,而且用其估计和预测的量也是不可信的.
(2)用公式计算,的值时,要先算出,然后才能算出.
3.利用回归方程,我们可以进行估计和预测.若回归方程为=x+,则x=x0处的估计值为0=x0+.
1.判断下列结论的正误(正确的打“√”,错误的打“×”)
(1)相关关系是两个变量之间的一种确定的关系. ( )
(2)回归直线方程一定过样本中心点. ( )
(3)选取一组数据的部分点得到的回归方程与由整组数据得到的回归方程一定相同. ( )
[答案] (1)× (2)√ (3)×
2.对有线性相关关系的两个变量建立的回归直线方程=+x中,回归系数( )
A.不能小于0 B.不能大于0
C.不能等于0 D.只能小于0
C [当=0时,不具有相关关系,可以大于0,也可以小于0.]
3.若施化肥量x(千克/亩)与水稻产量y(千克/亩)的回归方程为=5x+250,当施化肥量为80千克/亩时,预计水稻产量为亩产________千克左右.
650 [当x=80时,=400+250=650.]
4.元旦前夕,某市统计局统计了该市10户家庭的年收入和年饮食支出的统计资料如下表:
年收入 x(万元) 2 4 4 6 6 6 7 7 8 10
年饮食 支出y
(万元) 0.9 1.4 1.6 2.0 2.1 1.9 1.8 2.1 2.2 2.3
如果已知y与x是线性相关的,求回归方程.(参考数据:iyi=117.7,=406)
[解] 依题意可计算得:
=6,=1.83,2=36, =10.98,
又∵iyi=117.7,=406,
∴=≈0.17,=- =0.81,
∴=0.17x+0.81.
∴所求的回归方程为=0.17x+0.81.
2.3.1 变量之间的相关关系
2.3.2 两个变量的线性相关
学 习 目 标 核 心 素 养
1.了解变量间的相关关系,会画散点图,并利用散点图判断两个变量之间是否具有相关关系.(重点) 2.了解线性回归思想,会求回归直线方程.(难点) 1.通过对数据的分析、统计,培养数据分析素养.
2.借助变量间相关关系的研究,提升数学运算素养.
1.变量间的相关关系
(1)相关关系的定义
变量间确实存在关系,但又不具备函数关系所要求的确定性,它们的关系是带有不确定性的,那么这两个变量之间的关系叫做相关关系,两个变量之间的关系分为函数关系和相关关系.
(2)散点图
将样本中n个数据点(xi,yi)(i=1,2,…,n)描在平面直角坐标系中得到的图形叫做散点图.
(3)正相关与负相关
①正相关:如果一个变量的值由小变大时,另一个变量的值也由小变大,这种相关称为正相关.
②负相关:如果一个变量的值由小变大时,另一个变量的值由大变小,这种相关称为负相关.
2.回归直线方程
(1)回归直线:如果散点图中点的分布从整体上看大致在一条直线附近,就称这两个变量之间具有线性相关关系,这条直线叫做回归直线.
(2)线性回归方程:回归直线对应的方程叫做回归直线的方程,简称回归方程.
(3)最小二乘法:
求线性回归方程=x+时,使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法.
其中,是线性回归方程的斜率,是线性回归方程在y轴上的截距.
1.下列两个变量具有相关关系的是( )
A.角度和它的余弦值
B.圆的半径和该圆的面积
C.正n边形的边数和它的内角和
D.居民的收入与存款
D [A、B、C中两变量是确定的函数关系.]
2.某工厂某产品产量x(千件)与单位成本y(元)满足回归直线方程=77.36-1.82x,则以下说法中正确的是( )
A.产量每增加1 000件,单位成本约下降1.82元
B.产量每减少1 000件,单位成本约下降1.82元
C.当产量为1千件时,单位成本为75.54元
D.当产量为2千件时,单位成本为73.72元
A [令f(x)=77.36-1.82x,因为f(x+1)-f(x)=77.36-1.82(x+1)-77.36+1.82x=-1.82,所以产量每增加1 000件,单位成本约下降1.82元.]
3.5位学生的数学成绩和物理成绩如下表:
学科 A B C D E
数学 80 75 70 65 60
物理 70 66 68 64 62
则数学成绩与物理成绩之间( )
A.是函数关系
B.是相关关系,但相关性很弱
C.具有较好的相关关系,且是正相关
D.具有较好的相关关系,且是负相关
C [数学成绩x和物理成绩y的散点图如图所示.
从图上可以看出数学成绩和物理成绩具有较好的相关关系,且成正相关.]
4.设有一个回归方程为=2-1.5x,则变量x每增加1个单位时,y平均减少________个单位.
1.5 [因为=2-1.5x,所以变量x每增加1个单位时,y1-y2=[2-1.5(x+1)]-(2-1.5x)=-1.5,所以y平均减少1.5个单位.]
相关关系及判断
【例1】 某个男孩的年龄与身高的统计数据如下表所示.
年龄x(岁) 1 2 3 4 5 6
身高y(cm) 78 87 98 108 115 120
(1)画出散点图;
(2)判断y与x是否具有线性相关关系.
[解] (1)散点图如图所示.
(2)由图知,所有数据点接近一条直线排列,因此,认为y与x具有线性相关关系.
相关关系的判断方法
(1)两个变量x和y具有相关关系的判断方法
①散点图法:通过散点图,观察它们的分布是否存在一定规律,直观地判断;
②表格、关系式法:结合表格或关系式进行判断;
③经验法:借助积累的经验进行分析判断.
(2)判断两个变量x和y之间是否具有线性相关关系,常用的简便方法就是绘制散点图,如果发现点的分布从整体上看大致在一条直线附近,那么这两个变量就是线性相关的,注意不要受个别点的位置的影响.
1.下列关系中,属于相关关系的是________(填序号).
①正方形的边长与面积之间的关系;
②农作物的产量与施肥量之间的关系;
③出租车费与行驶的里程;
④降雪量与交通事故的发生率之间的关系.
②④ [在①中,正方形的边长与面积之间的关系是函数关系;在②中,农作物的产量与施肥量之间不具有严格的函数关系,但具有相关关系;③为确定的函数关系;在④中,降雪量与交通事故的发生率之间具有相关关系.]
求回归方程
[探究问题]
1.任意两个统计数据是否均可以作出散点图?
[提示] 任意两个统计数据均可以作出散点图.
2.任何一组数据都可以由最小二乘法得出回归方程吗?
[提示] 用最小二乘法求回归方程的前提是先判断所给数据具有线性相关关系,否则求回归方程是无意义的.
3.回归系数的含义是什么?
[提示] (1) 代表x每增加一个单位,y的平均增加单位数,而不是增加单位数.
(2)当>0时,两个变量呈正相关关系,含义为:x每增加一个单位,y平均增加个单位数;
当<0时,两个变量呈负相关关系,含义为:x每增加一个单位,y平均减少个单位数.
【例2】 一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,收集数据如下:
零件数x(个) 10 20 30 40 50 60 70 80 90 100
加工时间y(分) 62 68 75 81 89 95 102 108 115 122
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求y关于x的回归直线方程.
思路点拨:画散点图→确定相关关系→求回归直线系数→写回归直线方程.
[解] (1)画散点图如下:
由上图可知y与x具有线性相关关系.
(2)列表、计算:
i 1 2 3 4 5 6 7 8 9 10
xi 10 20 30 40 50 60 70 80 90 100
yi 62 68 75 81 89 95 102 108 115 122
xiyi 620 1 360 2 250 3 240 4 450 5 700 7 140 8 640 10 350 12 200
=55,=91.7, x=38 500,=87 777,iyi=55 950
求回归直线方程的步骤
(1)收集样本数据,设为(xi,yi)(i=1,2,…,n)(数据一般由题目给出).
(2)作出散点图,确定x,y具有线性相关关系.
2.某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x 2 4 5 6 8
y 30 40 60 50 70
(1)画出散点图;
(2)求回归方程.
[解] (1)散点图如图所示.
(2)列出下表,并用科学计算器进行有关计算.
i 1 2 3 4 5
xi 2 4 5 6 8
yi 30 40 60 50 70
xiyi 60 160 300 300 560
x 4 16 25 36 64
=5,=50,=145,iyi=1 380
于是可得,===6.5,
=-=50-6.5×5=17.5.
于是所求的回归方程是=6.5x+17.5.
回归方程的应用
【例3】 为了解某地区某种农产品的年产量x(单位:吨)对价格y(单位:千元/吨)的影响,对近五年该农产品的年产量和价格统计如表:
x 1 2 3 4 5
y 8 6 5 4 2
已知x和y具有线性相关关系.
(1)求,;
(2)求y关于x的线性回归方程=x+;
(3)若年产量为4.5吨,试预测该农产品的价格.
[解] (1)计算可得==3,==5.
因为线性回归直线过(,),则=-=5-(-1.4×3)=9.2,
故y关于x的线性回归方程是=-1.4x+9.2.
(3)当x=4.5时,=-1.4×4.5+9.2=2.9(千元/吨).
利用线性回归方程解题的常见思路及注意点
(1)利用回归直线过样本点的中心,可以求参数问题,参数可涉及回归方程或样本点数据.
(2)利用回归方程中系数的意义,分析实际问题.
(3)利用回归直线进行预测,此时需关注两点;①所得的值只是一个估计值,不是精确值;②变量x与y成线性相关关系时,线性回归方程才有意义,否则即使求出线性回归方程也是毫无意义的,用其估计和预测的量也是不可信的.
3.平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第90条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以100元罚款,记3分的行政处罚.如表是本市一主干路段监控设备所抓拍的5个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份 1 2 3 4 5
违章驾驶员人数 120 105 100 90 85
(1)请利用所给数据求违章人数y与月份x之间的回归直线方程=x+;
(2)预测该路段7月份的不“礼让斑马线”违章驾驶员人数.
[解] (1)由表中数据得,=×(1+2+3+4+5)=3,
=×(120+105+100+90+85)=100,
==
=
=-8.5,
=-b=100+8.5×3=125.5.
所以y与x之间的回归直线方程为y=-8.5x+125.5.
(2)x=7时,y=-8.5x+125.5=66,
预测该路段7月份的不“礼让斑马线”违章驾驶员人数为66人.
1.判断变量之间有无相关关系,简便可行的方法就是绘制散点图.根据散点图,可看出两个变量是否具有相关关系,是否线性相关,是正相关还是负相关.
2.求回归直线的方程时应注意的问题
(1)知道x与y呈线性相关关系,无需进行相关性检验,否则应首先进行相关性检验.如果两个变量之间本身不具有相关关系,或者说,它们之间的相关关系不显著,即使求出回归方程也是毫无意义的,而且用其估计和预测的量也是不可信的.
(2)用公式计算,的值时,要先算出,然后才能算出.
3.利用回归方程,我们可以进行估计和预测.若回归方程为=x+,则x=x0处的估计值为0=x0+.
1.判断下列结论的正误(正确的打“√”,错误的打“×”)
(1)相关关系是两个变量之间的一种确定的关系. ( )
(2)回归直线方程一定过样本中心点. ( )
(3)选取一组数据的部分点得到的回归方程与由整组数据得到的回归方程一定相同. ( )
[答案] (1)× (2)√ (3)×
2.对有线性相关关系的两个变量建立的回归直线方程=+x中,回归系数( )
A.不能小于0 B.不能大于0
C.不能等于0 D.只能小于0
C [当=0时,不具有相关关系,可以大于0,也可以小于0.]
3.若施化肥量x(千克/亩)与水稻产量y(千克/亩)的回归方程为=5x+250,当施化肥量为80千克/亩时,预计水稻产量为亩产________千克左右.
650 [当x=80时,=400+250=650.]
4.元旦前夕,某市统计局统计了该市10户家庭的年收入和年饮食支出的统计资料如下表:
年收入 x(万元) 2 4 4 6 6 6 7 7 8 10
年饮食 支出y
(万元) 0.9 1.4 1.6 2.0 2.1 1.9 1.8 2.1 2.2 2.3
如果已知y与x是线性相关的,求回归方程.(参考数据:iyi=117.7,=406)
[解] 依题意可计算得:
=6,=1.83,2=36, =10.98,
又∵iyi=117.7,=406,
∴=≈0.17,=- =0.81,
∴=0.17x+0.81.
∴所求的回归方程为=0.17x+0.81.
