2020-2021学年高中人教A版数学必修3学案 第2章 统计 章末综合提升 Word版含解析
文档属性
| 名称 | 2020-2021学年高中人教A版数学必修3学案 第2章 统计 章末综合提升 Word版含解析 |
|
|
| 格式 | doc | ||
| 文件大小 | 320.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 00:00:00 | ||
图片预览



文档简介
[巩固层·知识整合]
[提升层·题型探究]
用样本的频率分布估计总体分布
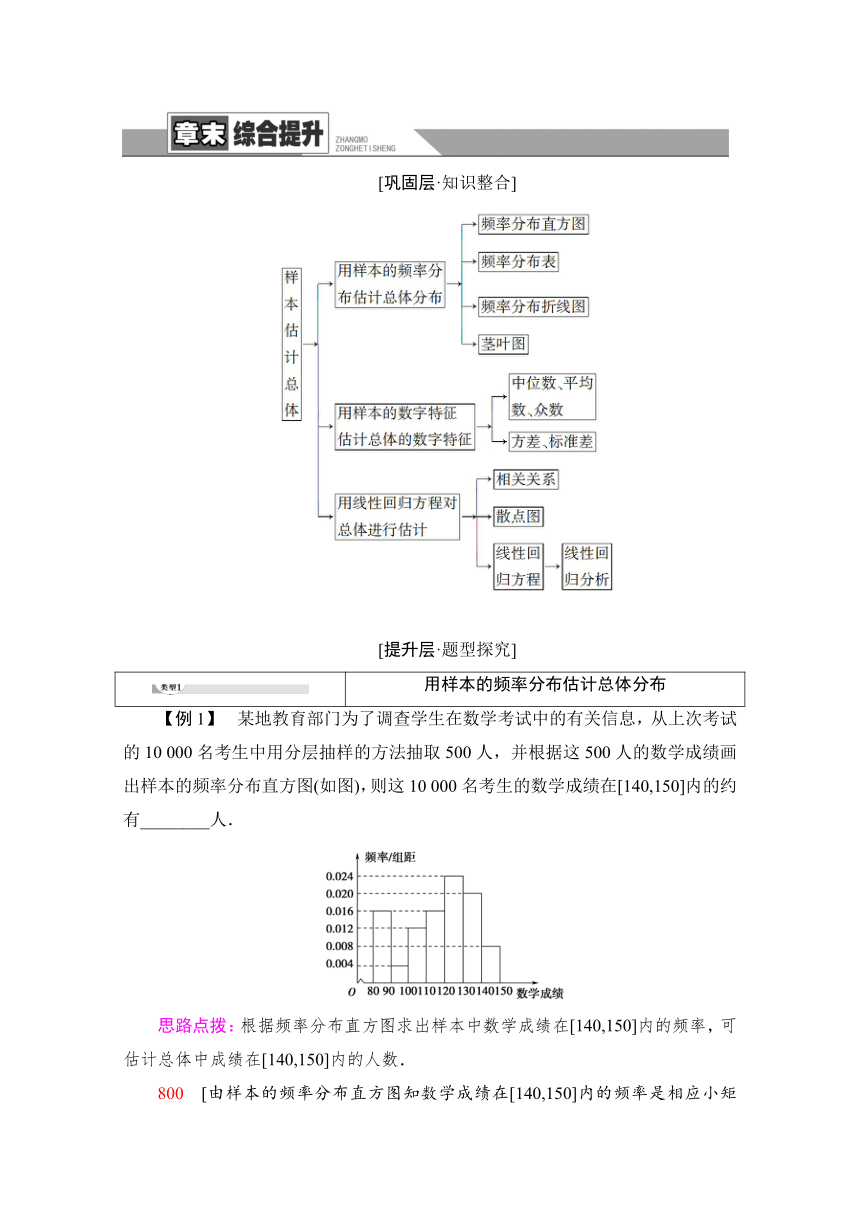
【例1】 某地教育部门为了调查学生在数学考试中的有关信息,从上次考试的10 000名考生中用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图),则这10 000名考生的数学成绩在[140,150]内的约有________人.
思路点拨:根据频率分布直方图求出样本中数学成绩在[140,150]内的频率,可估计总体中成绩在[140,150]内的人数.
800 [由样本的频率分布直方图知数学成绩在[140,150]内的频率是相应小矩形的面积,即0.008×10=0.08,因此这10 000名考生中数学成绩在[140,150]内的约有10 000×0.08=800(人).]
用样本的频率分布估计总体分布
通常要对样本数据进行列表、作图处理.这类问题采取的图表主要有:条形图、直方图、茎叶图、频率分布折线图、扇形图等.它们的主要优点是直观,能够清楚表示总体的分布走势.除茎叶图外,其他几种图表法的缺点是原始数据信息有丢失.
1.已知总体数据均在[10,70]内,从中抽取一个容量为20的样本,分组后对应组的频数如下表所示:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则总体数据在区间[10,50)内的频率约为( )
A.0.5 B.0.25
C.0.6 D.0.7
D [由频率分布表可知样本数据在区间[10,50)内的频数等于[10,20),[20,30),[30,40),[40,50)四个分组的频数之和,即2+3+4+5=14,频率为=0.7.
由样本的频率分布估计总体分布的思想可知,总体数据在区间[10,50)内的频率约为0.7.]
用样本的数字特征估计总体的数字特征
【例2】 在射击比赛中,甲、乙两名运动员分在同一小组,给出了他们命中的环数如下表:
甲 9 6 7 6 2 7 7 9 8 9
乙 2 4 6 8 7 8 9 7 9 10
赛后甲、乙两名运动员都说自己是胜者,如果你是裁判,你将给出怎样的评判?
思路点拨:规则不同,评判结果有所不同.
[解] 为了分析的方便,先计算两人的统计指标如下表所示.
平均环数 方差 中位数 命中10环次数
甲 7 4 7 0
乙 7 5.4 7.5 1
规则1:平均环数和方差相结合,平均环数高者胜.若平均环数相等,则再看方差,方差小者胜,则甲胜.
规则2:平均环数与中位数相结合,平均环数高者胜.若平均环数相等,则再看中位数,中位数大者胜,则乙胜.
规则3:平均环数与命中10环次数相结合,平均环数高者胜.若平均环数相等,则再看命中10环次数,命中10环次数多者胜,则乙胜.
以上规则都是以平均环数为第一标准,如果比赛规则是看命中7环以上或10环的次数,那么就不需要先看平均环数了.
样本的数字特征可分为两大类,一类反映样本数据的集中趋势,包括样本平均数、众数、中位数;另一类反映样本数据的波动大小,包括样本方差及标准差.通常,我们用样本的数字特征估计总体的数字特征.有关样本平均数及方差的计算和应用是高考考查的热点.
2.如图是某赛季甲、乙两名篮球运动员5场比赛得分的茎叶图,已知甲的成绩的极差为31,乙的成绩的平均值为24,则下列结论错误的是( )
A.x=9
B.y=8
C.乙的成绩的中位数为26
D.乙的成绩的方差小于甲的成绩的方差
B [甲的成绩极差为31,所以最高成绩为39.x=9;由乙平均值是24,得y=24×5-(12+25+26+31)-20=6;由茎叶图知乙成绩的中位数为26,对比甲、乙成绩分布发现,乙成绩较集中,其方差较小. ]
用线性回归方程对总体进行估计
【例3】 理论预测某城市2020到2024年人口总数与年份的关系如下表所示:
年份202x(年) 0 1 2 3 4
人口数y(十万) 5 7 8 11 19
(1)请画出上表数据的散点图;
(2)指出x与y是否线性相关;
(3)若x与y线性相关,请根据上表提供的数据,用最小二乘法求出y关于x的回归方程=x+;
(4)据此估计2025年该城市人口总数.
(参数数据:0×5+1×7+2×8+3×11+4×19=132,02+12+22+32+42=30)
[解] (1)数据的散点图如图:
(2)由散点图可知,样本点基本上分布在一条直线附近,故x与y呈线性相关.
(3)由表知:=×(0+1+2+3+4)=2,=×(5+7+8+11+19)=10.
∴==3.2,
=- =3.6,
∴回归方程为=3.2x+3.6.
(4)当x=5时,=19.6(十万)=196万.故2025年该城市人口总数约为196万.
对两个变量进行研究,通常是先作出两个变量之间的散点图,根据散点图直观判断两个变量是否具有线性相关关系,如果具有,就可以应用最小二乘法求线性回归直线方程.由于样本可以反映总体,所以可以利用所求的线性回归直线方程,对这两个变量所确定的总体进行估计,即根据一个变量的取值,预测另一个变量的取值.
3.随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 2016 2017 2018 2019 2020
时间代号t 1 2 3 4 5
储蓄存款y(千亿元) 5 6 7 8 10
(1)求y关于t的回归方程= t+;
(2)用所求回归方程预测该地区2021年(t=6)的人民币储蓄存款.
[解] (1)列表计算如下:
i ti yi t tiyi
1 1 5 1 5
2 2 6 4 12
3 3 7 9 21
4 4 8 16 32
5 5 10 25 50
∑ 15 36 55 120
这里n=5,=i==3,
=i==7.2.
-n2=55-5×32=10,
iyi-n =120-5×3×7.2=12,
从而==1.2,=- =7.2-1.2×3=3.6,
故所求回归方程为=1.2t+3.6.
(2)将t=6代入回归方程可预测该地区2021年的人民币储蓄存款为=1.2×6+3.6=10.8(千亿元).
[提升层·题型探究]
用样本的频率分布估计总体分布
【例1】 某地教育部门为了调查学生在数学考试中的有关信息,从上次考试的10 000名考生中用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图),则这10 000名考生的数学成绩在[140,150]内的约有________人.
思路点拨:根据频率分布直方图求出样本中数学成绩在[140,150]内的频率,可估计总体中成绩在[140,150]内的人数.
800 [由样本的频率分布直方图知数学成绩在[140,150]内的频率是相应小矩形的面积,即0.008×10=0.08,因此这10 000名考生中数学成绩在[140,150]内的约有10 000×0.08=800(人).]
用样本的频率分布估计总体分布
通常要对样本数据进行列表、作图处理.这类问题采取的图表主要有:条形图、直方图、茎叶图、频率分布折线图、扇形图等.它们的主要优点是直观,能够清楚表示总体的分布走势.除茎叶图外,其他几种图表法的缺点是原始数据信息有丢失.
1.已知总体数据均在[10,70]内,从中抽取一个容量为20的样本,分组后对应组的频数如下表所示:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则总体数据在区间[10,50)内的频率约为( )
A.0.5 B.0.25
C.0.6 D.0.7
D [由频率分布表可知样本数据在区间[10,50)内的频数等于[10,20),[20,30),[30,40),[40,50)四个分组的频数之和,即2+3+4+5=14,频率为=0.7.
由样本的频率分布估计总体分布的思想可知,总体数据在区间[10,50)内的频率约为0.7.]
用样本的数字特征估计总体的数字特征
【例2】 在射击比赛中,甲、乙两名运动员分在同一小组,给出了他们命中的环数如下表:
甲 9 6 7 6 2 7 7 9 8 9
乙 2 4 6 8 7 8 9 7 9 10
赛后甲、乙两名运动员都说自己是胜者,如果你是裁判,你将给出怎样的评判?
思路点拨:规则不同,评判结果有所不同.
[解] 为了分析的方便,先计算两人的统计指标如下表所示.
平均环数 方差 中位数 命中10环次数
甲 7 4 7 0
乙 7 5.4 7.5 1
规则1:平均环数和方差相结合,平均环数高者胜.若平均环数相等,则再看方差,方差小者胜,则甲胜.
规则2:平均环数与中位数相结合,平均环数高者胜.若平均环数相等,则再看中位数,中位数大者胜,则乙胜.
规则3:平均环数与命中10环次数相结合,平均环数高者胜.若平均环数相等,则再看命中10环次数,命中10环次数多者胜,则乙胜.
以上规则都是以平均环数为第一标准,如果比赛规则是看命中7环以上或10环的次数,那么就不需要先看平均环数了.
样本的数字特征可分为两大类,一类反映样本数据的集中趋势,包括样本平均数、众数、中位数;另一类反映样本数据的波动大小,包括样本方差及标准差.通常,我们用样本的数字特征估计总体的数字特征.有关样本平均数及方差的计算和应用是高考考查的热点.
2.如图是某赛季甲、乙两名篮球运动员5场比赛得分的茎叶图,已知甲的成绩的极差为31,乙的成绩的平均值为24,则下列结论错误的是( )
A.x=9
B.y=8
C.乙的成绩的中位数为26
D.乙的成绩的方差小于甲的成绩的方差
B [甲的成绩极差为31,所以最高成绩为39.x=9;由乙平均值是24,得y=24×5-(12+25+26+31)-20=6;由茎叶图知乙成绩的中位数为26,对比甲、乙成绩分布发现,乙成绩较集中,其方差较小. ]
用线性回归方程对总体进行估计
【例3】 理论预测某城市2020到2024年人口总数与年份的关系如下表所示:
年份202x(年) 0 1 2 3 4
人口数y(十万) 5 7 8 11 19
(1)请画出上表数据的散点图;
(2)指出x与y是否线性相关;
(3)若x与y线性相关,请根据上表提供的数据,用最小二乘法求出y关于x的回归方程=x+;
(4)据此估计2025年该城市人口总数.
(参数数据:0×5+1×7+2×8+3×11+4×19=132,02+12+22+32+42=30)
[解] (1)数据的散点图如图:
(2)由散点图可知,样本点基本上分布在一条直线附近,故x与y呈线性相关.
(3)由表知:=×(0+1+2+3+4)=2,=×(5+7+8+11+19)=10.
∴==3.2,
=- =3.6,
∴回归方程为=3.2x+3.6.
(4)当x=5时,=19.6(十万)=196万.故2025年该城市人口总数约为196万.
对两个变量进行研究,通常是先作出两个变量之间的散点图,根据散点图直观判断两个变量是否具有线性相关关系,如果具有,就可以应用最小二乘法求线性回归直线方程.由于样本可以反映总体,所以可以利用所求的线性回归直线方程,对这两个变量所确定的总体进行估计,即根据一个变量的取值,预测另一个变量的取值.
3.随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 2016 2017 2018 2019 2020
时间代号t 1 2 3 4 5
储蓄存款y(千亿元) 5 6 7 8 10
(1)求y关于t的回归方程= t+;
(2)用所求回归方程预测该地区2021年(t=6)的人民币储蓄存款.
[解] (1)列表计算如下:
i ti yi t tiyi
1 1 5 1 5
2 2 6 4 12
3 3 7 9 21
4 4 8 16 32
5 5 10 25 50
∑ 15 36 55 120
这里n=5,=i==3,
=i==7.2.
-n2=55-5×32=10,
iyi-n =120-5×3×7.2=12,
从而==1.2,=- =7.2-1.2×3=3.6,
故所求回归方程为=1.2t+3.6.
(2)将t=6代入回归方程可预测该地区2021年的人民币储蓄存款为=1.2×6+3.6=10.8(千亿元).
