17.2勾股定理的逆定理-2020-2021学年人教版八年级数学下册同步提升训练(word版含解析)
文档属性
| 名称 | 17.2勾股定理的逆定理-2020-2021学年人教版八年级数学下册同步提升训练(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 329.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 10:55:03 | ||
图片预览


文档简介
2020-2021年人教版八年级数学下册《17.2勾股定理的逆定理》同步提升训练(附答案)
1.下列各组线段中不能作为直角三角形三边长的是( )
A.1、、2 B.1、、 C.、2、 D.、、
2.下列说法不正确的是( )
A.△ABC中,若∠A﹣∠B=∠C,则△ABC是直角三角形
B.△ABC中,若b2﹣c2=a2,则△ABC是直角三角形
C.△ABC 的三边之比是5:12:13,则△ABC是直角三角形
D.△ABC中,若a2+b2≠c2,则△ABC不是直角三角形
3.下列各组数是勾股数的是( )
A.0.3,0.4,0.5 B.5,7,9
C.4,5,6 D.6,8,10
如果用,a、b、c表示△ABC的三边,那么分别满足下列条件的三角形中,直角三角形有( )
①b2=c2﹣a2②a:b:c=3:4:5③∠C=∠A﹣∠B④∠A:∠B:∠C=12:13:15
A.1个 B.2个 C.3个 D.4个
5.如图,已知△ABC中AC=24,AB=25,BC=7,AB上取一点E,AC上取一点F使得∠EFC=136°,过点B作BD∥EF,则∠CBD等于( )
A.44° B.56° C.46° D.68°
6.如图所示的是一种机器人行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m后往东一拐,仅走0.5m就到达了B.则点A与点B之间的直线距离是( )
A.10m B.8.5m C.7m D.6.5m
7.如图,在△ABC中,AB=5,BC=4,AC=3,点O是三条角平分线的交点,则△BOC的BC边上的高是( )
A.1 B.2 C.3 D.4
二.填空题(共12小题)
8.将一根长为24cm的筷子置于底面直径为12cm,高为16cm的圆柱形水杯中,则筷子露在杯子外面的最短长度为 cm.
9.如图,正方形网格中,点A,B,C,D均在格点上,则∠AOB+∠COD= °.
10.在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离(BC)有5米.则旗杆的高度 .
11.《九章算术》中有一个“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问折处高几尺?即:如图,AB+AC=9尺,BC=3尺,则AC 尺.
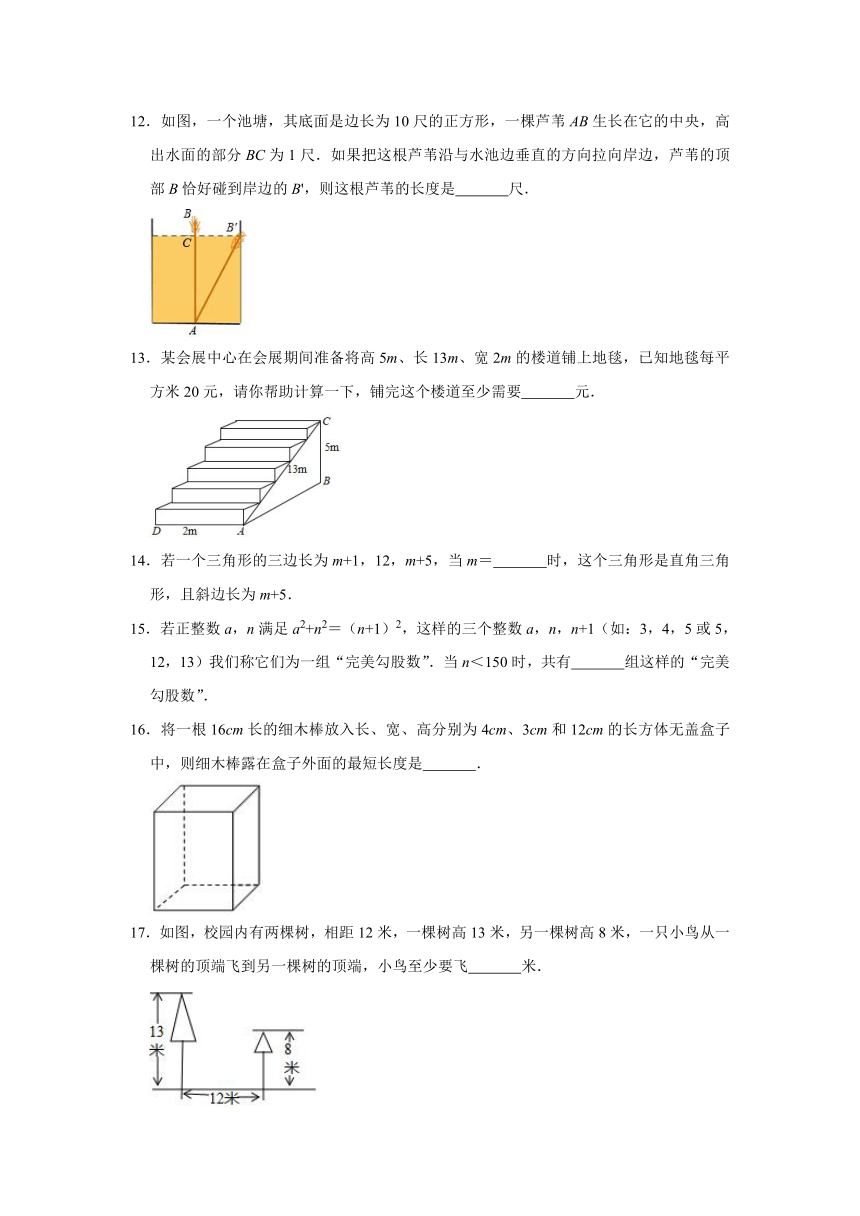
12.如图,一个池塘,其底面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面的部分BC为1尺.如果把这根芦苇沿与水池边垂直的方向拉向岸边,芦苇的顶部B恰好碰到岸边的B',则这根芦苇的长度是 尺.
13.某会展中心在会展期间准备将高5m、长13m、宽2m的楼道铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼道至少需要 元.
14.若一个三角形的三边长为m+1,12,m+5,当m= 时,这个三角形是直角三角形,且斜边长为m+5.
15.若正整数a,n满足a2+n2=(n+1)2,这样的三个整数a,n,n+1(如:3,4,5或5,12,13)我们称它们为一组“完美勾股数”.当n<150时,共有 组这样的“完美勾股数”.
16.将一根16cm长的细木棒放入长、宽、高分别为4cm、3cm和12cm的长方体无盖盒子中,则细木棒露在盒子外面的最短长度是 .
17.如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 米.
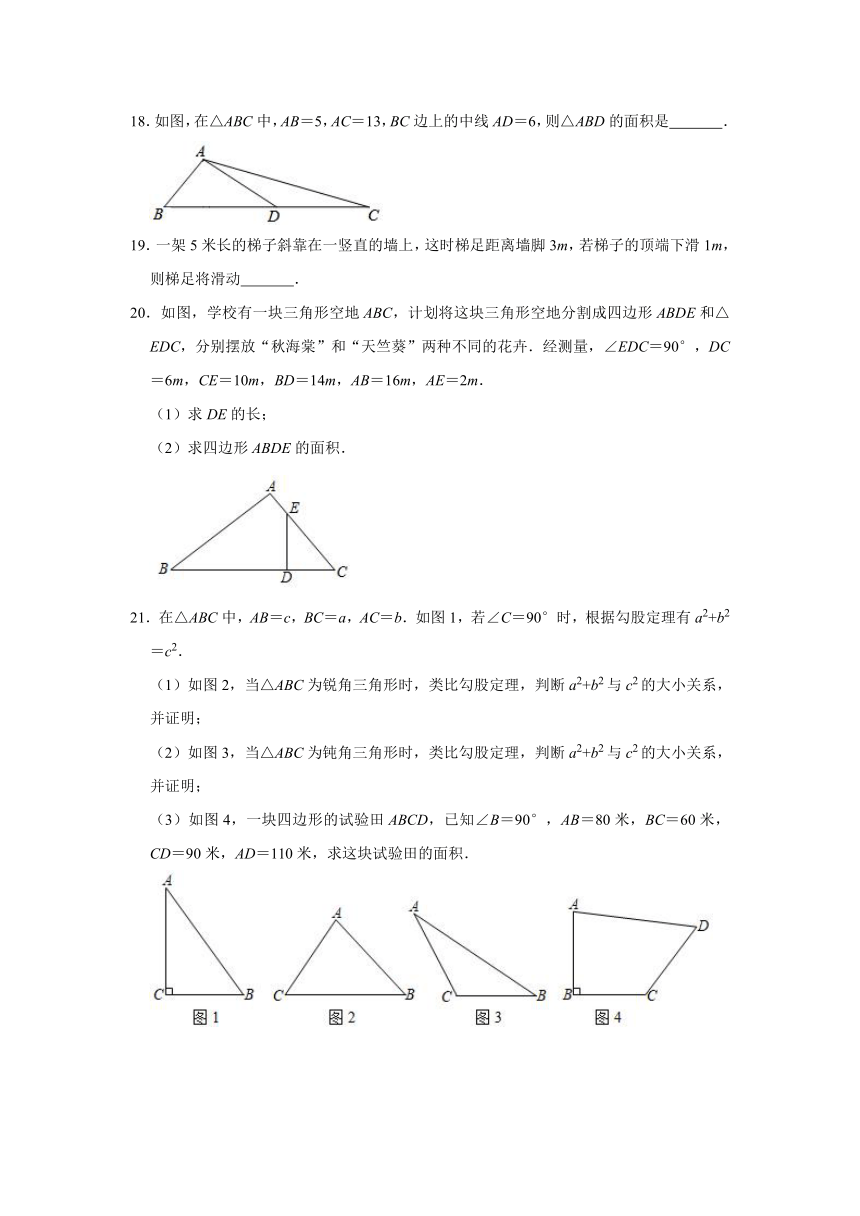
18.如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是 .
19.一架5米长的梯子斜靠在一竖直的墙上,这时梯足距离墙脚3m,若梯子的顶端下滑1m,则梯足将滑动 .
20.如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉.经测量,∠EDC=90°,DC=6m,CE=10m,BD=14m,AB=16m,AE=2m.
(1)求DE的长;
(2)求四边形ABDE的面积.
21.在△ABC中,AB=c,BC=a,AC=b.如图1,若∠C=90°时,根据勾股定理有a2+b2=c2.
(1)如图2,当△ABC为锐角三角形时,类比勾股定理,判断a2+b2与c2的大小关系,并证明;
(2)如图3,当△ABC为钝角三角形时,类比勾股定理,判断a2+b2与c2的大小关系,并证明;
(3)如图4,一块四边形的试验田ABCD,已知∠B=90°,AB=80米,BC=60米,CD=90米,AD=110米,求这块试验田的面积.
22.如图,把一块直角三角形(△ABC,∠ACB=90°)土地划出一个三角形(△ADC)后,测得CD=3米,AD=4米,BC=12米,AB=13米.
(1)求证:∠ADC=90°;
(2)求图中阴影部分土地的面积.
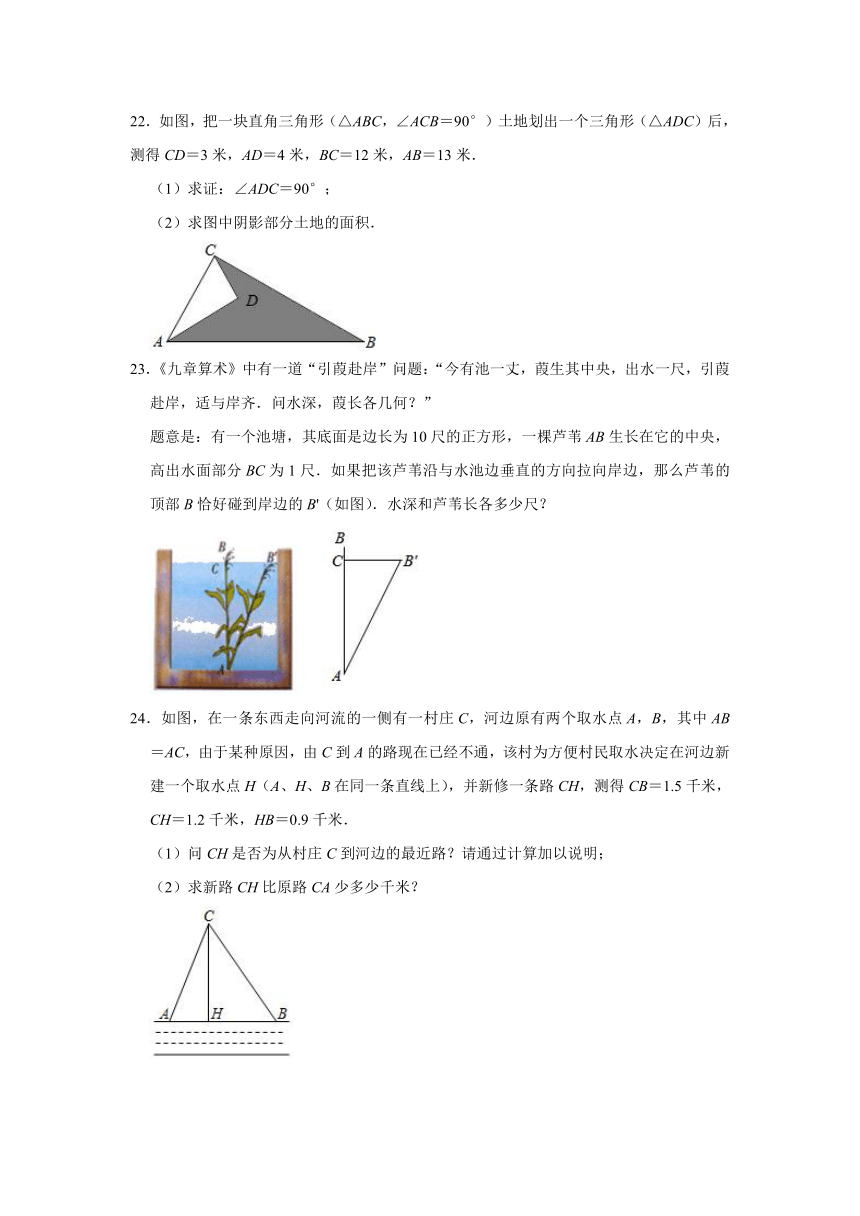
23.《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”
题意是:有一个池塘,其底面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(如图).水深和芦苇长各多少尺?
24.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
25.如图,某电信公司计划在A,B两乡镇间的E处修建一座5G信号塔,且使C,D两个村庄到E的距离相等.已知AD⊥AB于点A,BC⊥AB于点B,AB=80km,AD=50km,BC=30km,求5G信号塔E应该建在离A乡镇多少千米的地方?
26.如图,在正方形网格中,小正方形的边长为1,点A,B,C为网格的交点.
(1)判断△ABC的形状,并说明理由;
(2)求AB边上的高.
27.如图,在△ABC中,AB=5,AC=13,AD是边BC上的中线,点E在AD的延长线上,AD=ED=6.
(1)求证:△ABD≌△ECD;
(2)求△ABD的面积.
参考答案
1.解:A.∵12+()2≠22,
∴以1,,2为边不能组成直角三角形,故本选项符合题意;
B.∵12+()2=()2,
∴以1,,为边能组成直角三角形,故本选项不符合题意;
C.∵22+()2=()2,
∴以2,,为边能组成直角三角形,故本选项不符合题意;
D.∵()2+()2=()2,
∴以,,为边能组成直角三角形,故本选项不符合题意;
故选:A.
2.解:A、△ABC中,若∠A﹣∠B=∠C,可得,∠A=90°,则△ABC是直角三角形,说法正确,不符合题意;
B、△ABC中,若b2﹣c2=a2,可得,b2=c2+a2,则△ABC是直角三角形,说法正确,不符合题意;
C、△ABC 的三边之比是5:12:13,可得,(5x)2+(12x)2=(13x)2,则△ABC是直角三角形,说法正确,不符合题意;
D、△ABC中,若a2+b2≠c2,而b2=c2+a2,则△ABC是直角三角形,说法错误,符合题意;
故选:D.
3.解:A、∵0.32+0.42=0.52,但不是整数,∴这组数不是勾股数;
B、∵52+72≠92,∴这组数不是勾股数;
C、∵52+42≠62,∴这组数不是勾股数;
D、∵62+82=102,∴这组数是勾股数.
故选:D.
4.解:①b2=c2﹣a2,可以变形为b2+a2=c2,是直角三角形;
②∵a:b:c=3:4:5,
∴设a=3x,b=4x,c=5x,
∵(3x)2+(4x)2=(5x)2,
∴a2+b2=c2,
∴是直角三角形;
③∵∠C=∠A﹣∠B,
∴∠C+∠B=∠A,
∵∠C+∠B+∠A=180°,
∴∠A=90°,
∴是直角三角形;
④∵∠A:∠B:∠C=12:13:15,
∴设∠A=×180°≠90°
∴不是直角三角形;
则直角三角形有3个,
故选:C.
5.解:在△ABC中AC=24,AB=25,BC=7,
∵242+72=625=252,即AC2+BC2=AB2,
∴△ABC为直角三角形,
∴∠ACB=90°.
过点C作CM∥EF交AB于点M,则CM∥BD,如图所示.
∵CM∥EF,∠EFC=136°,
∴∠MCF=180°﹣∠EFC=44°,
∴∠BCM=∠ACB﹣∠MCF=46°.
又∵CM∥BD,
∴∠CBD=∠BCM=46°.
故选:C.
6.解:过点B作BC⊥AD于C,
从图中可以看出AC=4﹣2+0.5=2.5(m),
BC=4.5+1.5=6(m),
在直角△ABC中,AB为斜边,
则AB==6.5(m).
答:从点A到点B之间的距离是6.5m,
故选:D.
7.解:过O作OE⊥AC于E,OF⊥BC于F,OD⊥AB于D,
在△ABC中,BC=4,CA=3,AB=5,
∴△ABC是直角三角形,
∵点O为△ABC的三条角平分线的交点,
∴OE=OF=OD,
设OE=x,
∵S△ABC=S△OAB+S△OAC+S△OCB,
∴×4×3=OD×5+OE×3+OF×4,
∴5x+3x+4x=12,
∴x=1,
∴点O到BC的距离等于1.
即△BOC的BC边上的高是1,
故选:A.
8.解:设筷子露在杯子外面的长度为h,
当筷子与杯底及杯高构成直角三角形时h最小,
如图所示:此时,AB===20(cm),
故h=24﹣20=4(cm).
故筷子露在杯子外面的最短长度为4cm.
故答案为:4.
9.解:连接BC,
由勾股定理得:OC2=12+22=5,OB2=12+32=10,BC2=12+22,
∴OC=BC,OC2+BC2=OB2,
∴∠OCB=90°,
即△COB是等腰直角三角形,
∴∠COB=45°,
∵∠DOA=90°,
∴∠AOB+∠COD=∠DOA﹣∠COB=45°,
故答案为:45.
10.解:设旗杆的高度为x米,根据题意可得:
(x+1)2=x2+52,
解得:x=12,
答:旗杆的高度为12米.
故答案为:12米.
11.解:设竹子折断处离地面x尺,则斜边为(9﹣x)尺,
根据勾股定理得:x2+32=(9﹣x)2.
解得:x=4,
答:折断处离地面的高度为4尺.
故答案为:=4.
12.解:设芦苇长AB=AB′=x尺,则水深AC=(x﹣1)尺,
因为边长为10尺的正方形,所以B'C=5尺
在Rt△AB'C中,52+(x﹣1)2=x2,
解之得x=13,
即芦苇长13尺.
故答案是:13.
13.解:由勾股定理得AB===12(m),
则地毯总长为12+5=17(m),
则地毯的总面积为17×2=34(平方米),
所以铺完这个楼道至少需要34×20=680(元).
故答案为:680.
14.解:由题意可得,(m+1)2+122=(m+5)2,
解得m=15.
故答案为:15.
15.解:∵n<150,(n+1)2﹣n2=2n+1,
又∵149+150=299,大于等于9小于297的非偶数完全平方数有9,25,49,81,121,169,225,289,一共8个,
∴共有8组这样的“完美勾股数”.
故答案为:8.
16.解:如图,由题意知:盒子底面对角长为=5(cm),
盒子的对角线长:=13(cm),
∵细木棒长16cm,
∴细木棒露在盒外面的最短长度是:16﹣13=3cm.
故答案为:3cm.
17.解:如图所示,AB,CD为树,且AB=13米,CD=8米,BD为两树距离12米,
过C作CE⊥AB于E,
则CE=BD=12AE=AB﹣CD=5,
在直角三角形AEC中,
斜边长AC==13米,即小鸟至少要飞13米.
故答案为13.
18.解:延长AD到点E,使DE=AD=6,连接CE,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△CED中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB=5,∠BAD=∠E,
∵AE=2AD=12,CE=5,AC=13,
∴CE2+AE2=AC2,
∴∠E=90°,
∴∠BAD=90°,
即△ABD为直角三角形,
∴△ABD的面积=AD?AB=15,
故答案为:15.
19.解:依照题意画出图形,如图所示.
在Rt△AOB中,OB=3m,AB=5m,
∴OA==4m.
在Rt△COD中,OC=OA﹣AC=3m,CD=AB=5m,
∴OD==4m,
∴BD=OD﹣OB=4﹣3=1m.
故答案为:1m.
20.解:(1)在Rt△EDC中,∠EDC=90°,DC=6m,CE=10m,
∴m;
(2)如图,连接BE,
在Rt△EBD中,BD=14m,ED=8m,
∴BE2=BD2+ED2=142+82=260,
∵AB=16m,AE=2m,
∴AB2+AE2=162+22=260,
∴AB2+AE2=BE2,
∴△ABE是直角三角形,∠A=90°,
∴S△ABE=×16×2=16(m2).
又∵S△BDE=×14×8=56(m2).
∴四边形ABDE的面积=S△ABE+S△BDE=72(m2).
21.解:(1)a2+b2>c2,
理由如下:过点A作AD⊥BC 于D,
设CD=x,则BD=a﹣x,
由勾股定理得,b2﹣x2=AD2,c2﹣(a﹣x)2=AD2,
∴b2﹣x2=c2﹣(a﹣x)2,
整理得:a2+b2=c2+2ax,
∵2ax>0,
∴a2+b2>c2;
(2)a2+b2<c2,
理由如下:作AE⊥BC交BC的延长线于E,
设CE=x,
则c2﹣(a+x)2=AE2=b2﹣x2,
整理得:a2+b2=c2﹣2ax,
∵2ax>0,
∴a2+b2<c2;
(3)连接AC,作DF⊥AC于F,
由勾股定理得,AC==100,
由(1)可知,AD2﹣AF2=DC2﹣CF2,即1102﹣(100﹣CF)2=902﹣CF2,
解得,CF=30,
则DF==60,
∴这块试验田的面积=×60×80+×100×60=(2400+3000)米2
22.(1)证明:∵∠ACB=90°,BC=12米,AB=13米,
∴AC===5(米),
∵CD=3米,AD=4米,
∴AD2+CD2=AC2=25,
∴∠ADC=90°;
(2)解:图中阴影部分土地的面积=A×BC﹣AD×CD=×5×12﹣×4×3=24(平方米).
23.解:设水深x尺,则芦苇长(x+1)尺.
由题意得x2+52=(x+1)2.
解得x=12.
∴x+1=13.
答:水深12尺;芦苇长13尺.
24.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(1.2)2+(0.9)2=2.25,
BC2=2.25,
∴CH2+BH2=BC2,
∴CH⊥AB,
所以CH是从村庄C到河边的最近路;
(2)设AC=x千米,
在Rt△ACH中,由已知得AC=x,AH=x﹣0.9,CH=1.2,
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣0.9)2+(1.2)2,
解这个方程,得x=1.25,
1.25﹣1.2=0.05(千米)
答:新路CH比原路CA少0.05千米.
25.解:设AE=xkm,则BE=(80﹣x)km,
∵AD⊥AB,BC⊥AB,
∴△ADE和△BCE都是直角三角形,
∴DE2=AD2+AE2,CE2=BE2+BC2,
又∵AD=50,BC=30,DE=CE,
∴502+x2=(80﹣x)2+302,
解得x=30.
答:5G信号塔E应该建在离A乡镇30千米的地方.
26.解:(1)△ABC为直角三角形,
理由:由图可知,
,BC=,AB==5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)设AB边上的高为h,
由(1)知,,BC=,AB=5,△ABC是直角三角形,
∴=,
即=h,
解得,h=2,
即AB边上的高为2.
27.证明:(1)∵AD是边BC上的中线,
∴BD=CD,
在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
(2)∵△ABD≌△ECD,
∴AB=CE=5,
∵AE=AD+ED=12,AC=13,CE=5,
∴AE2+CE2=AC2,
∴△ACE是直角三角形,
∴△ABC的面积=△ACE的面积=×5×12=30,
∴△ABD的面积=△ABC的面积=15
1.下列各组线段中不能作为直角三角形三边长的是( )
A.1、、2 B.1、、 C.、2、 D.、、
2.下列说法不正确的是( )
A.△ABC中,若∠A﹣∠B=∠C,则△ABC是直角三角形
B.△ABC中,若b2﹣c2=a2,则△ABC是直角三角形
C.△ABC 的三边之比是5:12:13,则△ABC是直角三角形
D.△ABC中,若a2+b2≠c2,则△ABC不是直角三角形
3.下列各组数是勾股数的是( )
A.0.3,0.4,0.5 B.5,7,9
C.4,5,6 D.6,8,10
如果用,a、b、c表示△ABC的三边,那么分别满足下列条件的三角形中,直角三角形有( )
①b2=c2﹣a2②a:b:c=3:4:5③∠C=∠A﹣∠B④∠A:∠B:∠C=12:13:15
A.1个 B.2个 C.3个 D.4个
5.如图,已知△ABC中AC=24,AB=25,BC=7,AB上取一点E,AC上取一点F使得∠EFC=136°,过点B作BD∥EF,则∠CBD等于( )
A.44° B.56° C.46° D.68°
6.如图所示的是一种机器人行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m后往东一拐,仅走0.5m就到达了B.则点A与点B之间的直线距离是( )
A.10m B.8.5m C.7m D.6.5m
7.如图,在△ABC中,AB=5,BC=4,AC=3,点O是三条角平分线的交点,则△BOC的BC边上的高是( )
A.1 B.2 C.3 D.4
二.填空题(共12小题)
8.将一根长为24cm的筷子置于底面直径为12cm,高为16cm的圆柱形水杯中,则筷子露在杯子外面的最短长度为 cm.
9.如图,正方形网格中,点A,B,C,D均在格点上,则∠AOB+∠COD= °.
10.在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离(BC)有5米.则旗杆的高度 .
11.《九章算术》中有一个“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问折处高几尺?即:如图,AB+AC=9尺,BC=3尺,则AC 尺.
12.如图,一个池塘,其底面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面的部分BC为1尺.如果把这根芦苇沿与水池边垂直的方向拉向岸边,芦苇的顶部B恰好碰到岸边的B',则这根芦苇的长度是 尺.
13.某会展中心在会展期间准备将高5m、长13m、宽2m的楼道铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼道至少需要 元.
14.若一个三角形的三边长为m+1,12,m+5,当m= 时,这个三角形是直角三角形,且斜边长为m+5.
15.若正整数a,n满足a2+n2=(n+1)2,这样的三个整数a,n,n+1(如:3,4,5或5,12,13)我们称它们为一组“完美勾股数”.当n<150时,共有 组这样的“完美勾股数”.
16.将一根16cm长的细木棒放入长、宽、高分别为4cm、3cm和12cm的长方体无盖盒子中,则细木棒露在盒子外面的最短长度是 .
17.如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 米.
18.如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是 .
19.一架5米长的梯子斜靠在一竖直的墙上,这时梯足距离墙脚3m,若梯子的顶端下滑1m,则梯足将滑动 .
20.如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉.经测量,∠EDC=90°,DC=6m,CE=10m,BD=14m,AB=16m,AE=2m.
(1)求DE的长;
(2)求四边形ABDE的面积.
21.在△ABC中,AB=c,BC=a,AC=b.如图1,若∠C=90°时,根据勾股定理有a2+b2=c2.
(1)如图2,当△ABC为锐角三角形时,类比勾股定理,判断a2+b2与c2的大小关系,并证明;
(2)如图3,当△ABC为钝角三角形时,类比勾股定理,判断a2+b2与c2的大小关系,并证明;
(3)如图4,一块四边形的试验田ABCD,已知∠B=90°,AB=80米,BC=60米,CD=90米,AD=110米,求这块试验田的面积.
22.如图,把一块直角三角形(△ABC,∠ACB=90°)土地划出一个三角形(△ADC)后,测得CD=3米,AD=4米,BC=12米,AB=13米.
(1)求证:∠ADC=90°;
(2)求图中阴影部分土地的面积.
23.《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”
题意是:有一个池塘,其底面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(如图).水深和芦苇长各多少尺?
24.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
25.如图,某电信公司计划在A,B两乡镇间的E处修建一座5G信号塔,且使C,D两个村庄到E的距离相等.已知AD⊥AB于点A,BC⊥AB于点B,AB=80km,AD=50km,BC=30km,求5G信号塔E应该建在离A乡镇多少千米的地方?
26.如图,在正方形网格中,小正方形的边长为1,点A,B,C为网格的交点.
(1)判断△ABC的形状,并说明理由;
(2)求AB边上的高.
27.如图,在△ABC中,AB=5,AC=13,AD是边BC上的中线,点E在AD的延长线上,AD=ED=6.
(1)求证:△ABD≌△ECD;
(2)求△ABD的面积.
参考答案
1.解:A.∵12+()2≠22,
∴以1,,2为边不能组成直角三角形,故本选项符合题意;
B.∵12+()2=()2,
∴以1,,为边能组成直角三角形,故本选项不符合题意;
C.∵22+()2=()2,
∴以2,,为边能组成直角三角形,故本选项不符合题意;
D.∵()2+()2=()2,
∴以,,为边能组成直角三角形,故本选项不符合题意;
故选:A.
2.解:A、△ABC中,若∠A﹣∠B=∠C,可得,∠A=90°,则△ABC是直角三角形,说法正确,不符合题意;
B、△ABC中,若b2﹣c2=a2,可得,b2=c2+a2,则△ABC是直角三角形,说法正确,不符合题意;
C、△ABC 的三边之比是5:12:13,可得,(5x)2+(12x)2=(13x)2,则△ABC是直角三角形,说法正确,不符合题意;
D、△ABC中,若a2+b2≠c2,而b2=c2+a2,则△ABC是直角三角形,说法错误,符合题意;
故选:D.
3.解:A、∵0.32+0.42=0.52,但不是整数,∴这组数不是勾股数;
B、∵52+72≠92,∴这组数不是勾股数;
C、∵52+42≠62,∴这组数不是勾股数;
D、∵62+82=102,∴这组数是勾股数.
故选:D.
4.解:①b2=c2﹣a2,可以变形为b2+a2=c2,是直角三角形;
②∵a:b:c=3:4:5,
∴设a=3x,b=4x,c=5x,
∵(3x)2+(4x)2=(5x)2,
∴a2+b2=c2,
∴是直角三角形;
③∵∠C=∠A﹣∠B,
∴∠C+∠B=∠A,
∵∠C+∠B+∠A=180°,
∴∠A=90°,
∴是直角三角形;
④∵∠A:∠B:∠C=12:13:15,
∴设∠A=×180°≠90°
∴不是直角三角形;
则直角三角形有3个,
故选:C.
5.解:在△ABC中AC=24,AB=25,BC=7,
∵242+72=625=252,即AC2+BC2=AB2,
∴△ABC为直角三角形,
∴∠ACB=90°.
过点C作CM∥EF交AB于点M,则CM∥BD,如图所示.
∵CM∥EF,∠EFC=136°,
∴∠MCF=180°﹣∠EFC=44°,
∴∠BCM=∠ACB﹣∠MCF=46°.
又∵CM∥BD,
∴∠CBD=∠BCM=46°.
故选:C.
6.解:过点B作BC⊥AD于C,
从图中可以看出AC=4﹣2+0.5=2.5(m),
BC=4.5+1.5=6(m),
在直角△ABC中,AB为斜边,
则AB==6.5(m).
答:从点A到点B之间的距离是6.5m,
故选:D.
7.解:过O作OE⊥AC于E,OF⊥BC于F,OD⊥AB于D,
在△ABC中,BC=4,CA=3,AB=5,
∴△ABC是直角三角形,
∵点O为△ABC的三条角平分线的交点,
∴OE=OF=OD,
设OE=x,
∵S△ABC=S△OAB+S△OAC+S△OCB,
∴×4×3=OD×5+OE×3+OF×4,
∴5x+3x+4x=12,
∴x=1,
∴点O到BC的距离等于1.
即△BOC的BC边上的高是1,
故选:A.
8.解:设筷子露在杯子外面的长度为h,
当筷子与杯底及杯高构成直角三角形时h最小,
如图所示:此时,AB===20(cm),
故h=24﹣20=4(cm).
故筷子露在杯子外面的最短长度为4cm.
故答案为:4.
9.解:连接BC,
由勾股定理得:OC2=12+22=5,OB2=12+32=10,BC2=12+22,
∴OC=BC,OC2+BC2=OB2,
∴∠OCB=90°,
即△COB是等腰直角三角形,
∴∠COB=45°,
∵∠DOA=90°,
∴∠AOB+∠COD=∠DOA﹣∠COB=45°,
故答案为:45.
10.解:设旗杆的高度为x米,根据题意可得:
(x+1)2=x2+52,
解得:x=12,
答:旗杆的高度为12米.
故答案为:12米.
11.解:设竹子折断处离地面x尺,则斜边为(9﹣x)尺,
根据勾股定理得:x2+32=(9﹣x)2.
解得:x=4,
答:折断处离地面的高度为4尺.
故答案为:=4.
12.解:设芦苇长AB=AB′=x尺,则水深AC=(x﹣1)尺,
因为边长为10尺的正方形,所以B'C=5尺
在Rt△AB'C中,52+(x﹣1)2=x2,
解之得x=13,
即芦苇长13尺.
故答案是:13.
13.解:由勾股定理得AB===12(m),
则地毯总长为12+5=17(m),
则地毯的总面积为17×2=34(平方米),
所以铺完这个楼道至少需要34×20=680(元).
故答案为:680.
14.解:由题意可得,(m+1)2+122=(m+5)2,
解得m=15.
故答案为:15.
15.解:∵n<150,(n+1)2﹣n2=2n+1,
又∵149+150=299,大于等于9小于297的非偶数完全平方数有9,25,49,81,121,169,225,289,一共8个,
∴共有8组这样的“完美勾股数”.
故答案为:8.
16.解:如图,由题意知:盒子底面对角长为=5(cm),
盒子的对角线长:=13(cm),
∵细木棒长16cm,
∴细木棒露在盒外面的最短长度是:16﹣13=3cm.
故答案为:3cm.
17.解:如图所示,AB,CD为树,且AB=13米,CD=8米,BD为两树距离12米,
过C作CE⊥AB于E,
则CE=BD=12AE=AB﹣CD=5,
在直角三角形AEC中,
斜边长AC==13米,即小鸟至少要飞13米.
故答案为13.
18.解:延长AD到点E,使DE=AD=6,连接CE,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△CED中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB=5,∠BAD=∠E,
∵AE=2AD=12,CE=5,AC=13,
∴CE2+AE2=AC2,
∴∠E=90°,
∴∠BAD=90°,
即△ABD为直角三角形,
∴△ABD的面积=AD?AB=15,
故答案为:15.
19.解:依照题意画出图形,如图所示.
在Rt△AOB中,OB=3m,AB=5m,
∴OA==4m.
在Rt△COD中,OC=OA﹣AC=3m,CD=AB=5m,
∴OD==4m,
∴BD=OD﹣OB=4﹣3=1m.
故答案为:1m.
20.解:(1)在Rt△EDC中,∠EDC=90°,DC=6m,CE=10m,
∴m;
(2)如图,连接BE,
在Rt△EBD中,BD=14m,ED=8m,
∴BE2=BD2+ED2=142+82=260,
∵AB=16m,AE=2m,
∴AB2+AE2=162+22=260,
∴AB2+AE2=BE2,
∴△ABE是直角三角形,∠A=90°,
∴S△ABE=×16×2=16(m2).
又∵S△BDE=×14×8=56(m2).
∴四边形ABDE的面积=S△ABE+S△BDE=72(m2).
21.解:(1)a2+b2>c2,
理由如下:过点A作AD⊥BC 于D,
设CD=x,则BD=a﹣x,
由勾股定理得,b2﹣x2=AD2,c2﹣(a﹣x)2=AD2,
∴b2﹣x2=c2﹣(a﹣x)2,
整理得:a2+b2=c2+2ax,
∵2ax>0,
∴a2+b2>c2;
(2)a2+b2<c2,
理由如下:作AE⊥BC交BC的延长线于E,
设CE=x,
则c2﹣(a+x)2=AE2=b2﹣x2,
整理得:a2+b2=c2﹣2ax,
∵2ax>0,
∴a2+b2<c2;
(3)连接AC,作DF⊥AC于F,
由勾股定理得,AC==100,
由(1)可知,AD2﹣AF2=DC2﹣CF2,即1102﹣(100﹣CF)2=902﹣CF2,
解得,CF=30,
则DF==60,
∴这块试验田的面积=×60×80+×100×60=(2400+3000)米2
22.(1)证明:∵∠ACB=90°,BC=12米,AB=13米,
∴AC===5(米),
∵CD=3米,AD=4米,
∴AD2+CD2=AC2=25,
∴∠ADC=90°;
(2)解:图中阴影部分土地的面积=A×BC﹣AD×CD=×5×12﹣×4×3=24(平方米).
23.解:设水深x尺,则芦苇长(x+1)尺.
由题意得x2+52=(x+1)2.
解得x=12.
∴x+1=13.
答:水深12尺;芦苇长13尺.
24.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(1.2)2+(0.9)2=2.25,
BC2=2.25,
∴CH2+BH2=BC2,
∴CH⊥AB,
所以CH是从村庄C到河边的最近路;
(2)设AC=x千米,
在Rt△ACH中,由已知得AC=x,AH=x﹣0.9,CH=1.2,
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣0.9)2+(1.2)2,
解这个方程,得x=1.25,
1.25﹣1.2=0.05(千米)
答:新路CH比原路CA少0.05千米.
25.解:设AE=xkm,则BE=(80﹣x)km,
∵AD⊥AB,BC⊥AB,
∴△ADE和△BCE都是直角三角形,
∴DE2=AD2+AE2,CE2=BE2+BC2,
又∵AD=50,BC=30,DE=CE,
∴502+x2=(80﹣x)2+302,
解得x=30.
答:5G信号塔E应该建在离A乡镇30千米的地方.
26.解:(1)△ABC为直角三角形,
理由:由图可知,
,BC=,AB==5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)设AB边上的高为h,
由(1)知,,BC=,AB=5,△ABC是直角三角形,
∴=,
即=h,
解得,h=2,
即AB边上的高为2.
27.证明:(1)∵AD是边BC上的中线,
∴BD=CD,
在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
(2)∵△ABD≌△ECD,
∴AB=CE=5,
∵AE=AD+ED=12,AC=13,CE=5,
∴AE2+CE2=AC2,
∴△ACE是直角三角形,
∴△ABC的面积=△ACE的面积=×5×12=30,
∴△ABD的面积=△ABC的面积=15
