18.1平行四边形-2020-2021学年人教版八年级数学下册同步提升训练试卷(Word版含答案)
文档属性
| 名称 | 18.1平行四边形-2020-2021学年人教版八年级数学下册同步提升训练试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 336.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 15:13:25 | ||
图片预览


文档简介
2020-2021年人教版八年级数学下册《18.1平行四边形》同步提升训练(附答案)
1.如图,平行四边形ABCD中,E、F分别在边BC、AD上,添加条件后不能使AE=CF的是( )
A.BE=DF B.AE∥CF
C.AF=AE D.四边形AECF为平行四边形
2.如图,四边形ABCD中,AB=1,CD=4,M、N分别是AD、BC的中点,则线段MN的取值范围是( )
A.3<MN<5 B.3<MN≤5 C.<MN< D.<MN≤
3.如图,?ABCD的周长为36cm,△ABC的周长为28cm,则对角线AC的长为( )
A.28cm B.18cm C.10cm D.8cm
4.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3 B.2 C.4 D.2
5.在?ABCD中,已知∠A﹣∠B=20°,则∠C=( )
A.60° B.80° C.100° D.120°
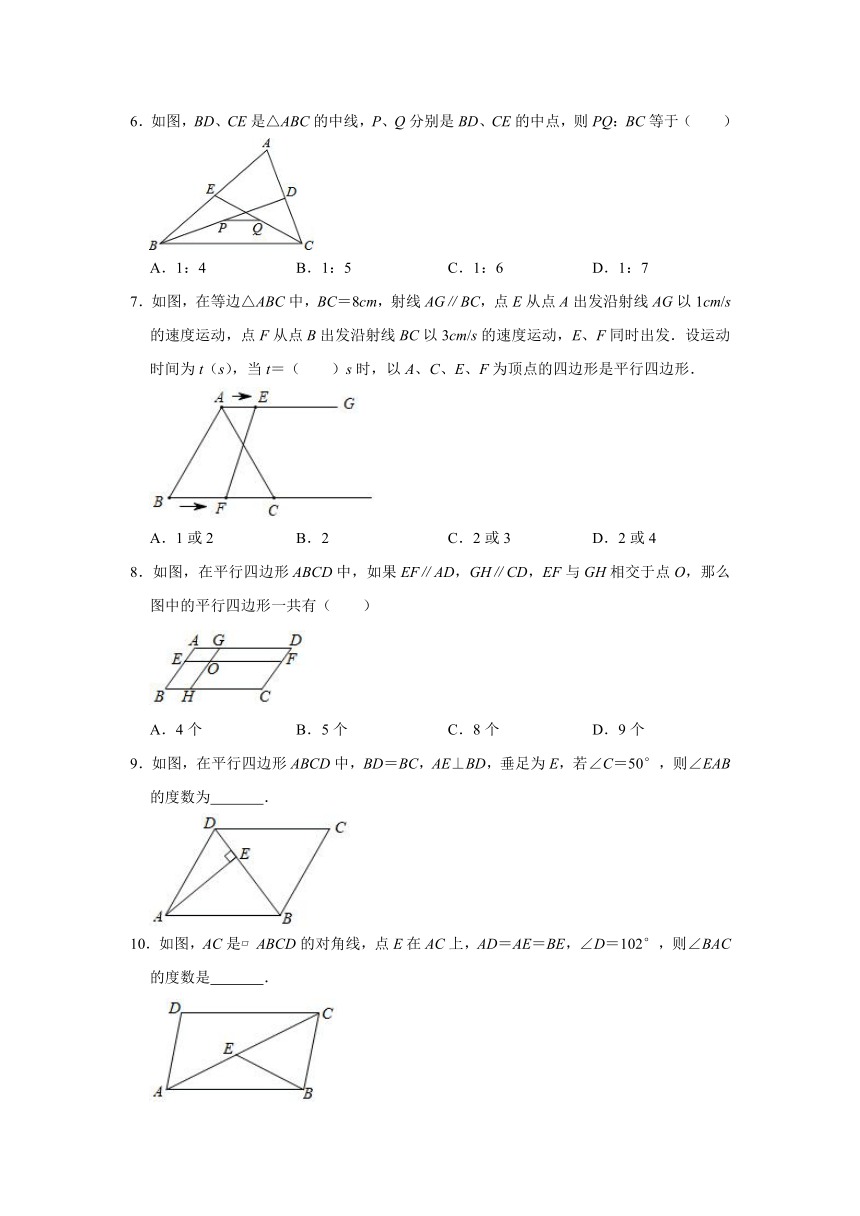
6.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
A.1:4 B.1:5 C.1:6 D.1:7
7.如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以3cm/s的速度运动,E、F同时出发.设运动时间为t(s),当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A.1或2 B.2 C.2或3 D.2或4
8.如图,在平行四边形ABCD中,如果EF∥AD,GH∥CD,EF与GH相交于点O,那么图中的平行四边形一共有( )
A.4个 B.5个 C.8个 D.9个
9.如图,在平行四边形ABCD中,BD=BC,AE⊥BD,垂足为E,若∠C=50°,则∠EAB的度数为 .
10.如图,AC是?ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的度数是 .
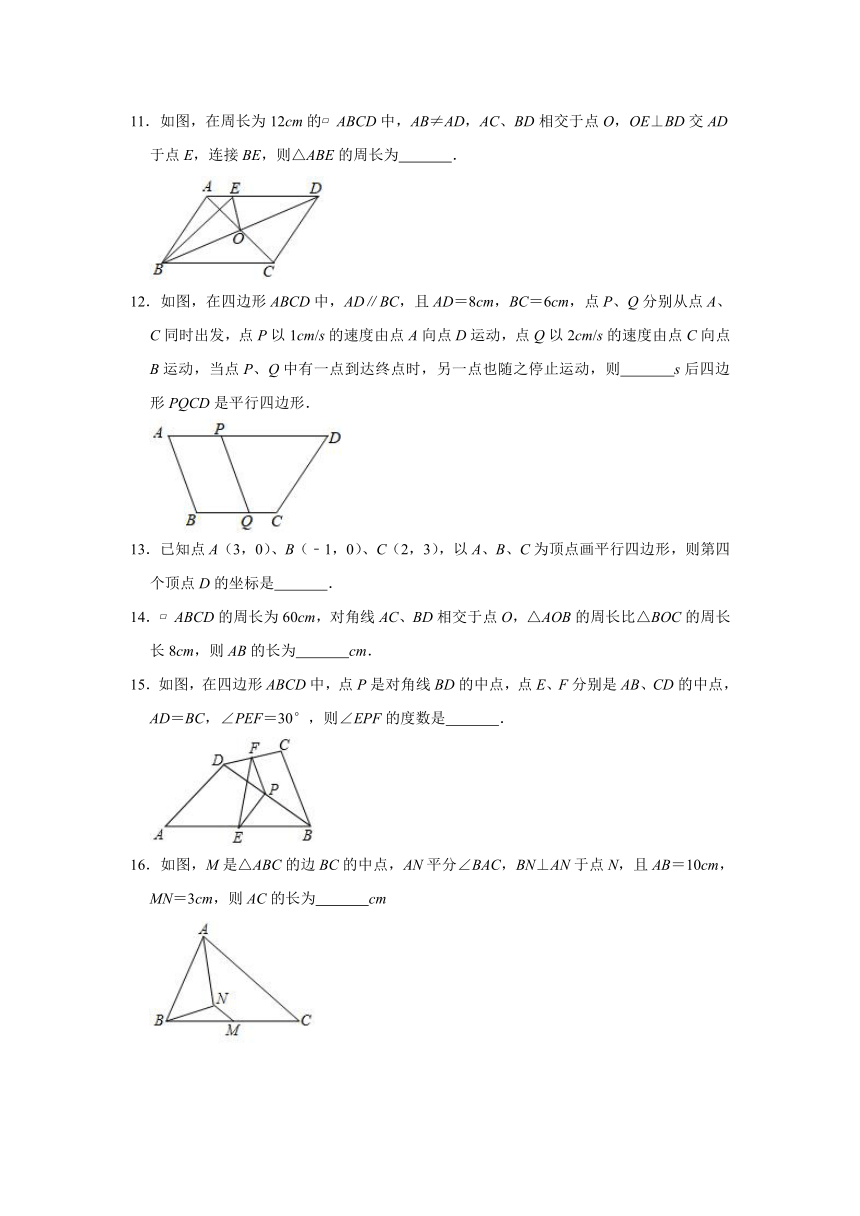
11.如图,在周长为12cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为 .
12.如图,在四边形ABCD中,AD∥BC,且AD=8cm,BC=6cm,点P、Q分别从点A、C同时出发,点P以1cm/s的速度由点A向点D运动,点Q以2cm/s的速度由点C向点B运动,当点P、Q中有一点到达终点时,另一点也随之停止运动,则 s后四边形PQCD是平行四边形.
13.已知点A(3,0)、B(﹣1,0)、C(2,3),以A、B、C为顶点画平行四边形,则第四个顶点D的坐标是 .
14.?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,则AB的长为 cm.
15.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是 .
16.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=10cm,MN=3cm,则AC的长为 cm
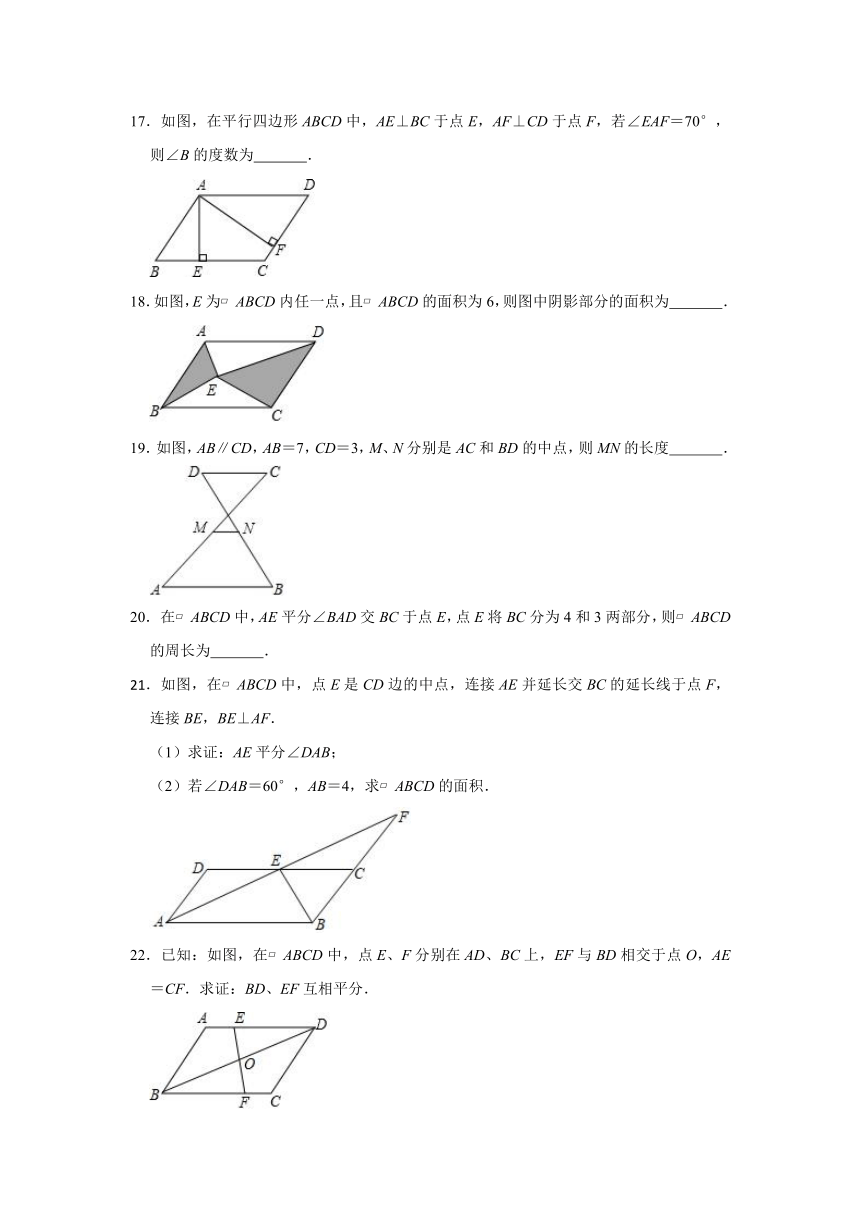
17.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=70°,则∠B的度数为 .
18.如图,E为?ABCD内任一点,且?ABCD的面积为6,则图中阴影部分的面积为 .
19.如图,AB∥CD,AB=7,CD=3,M、N分别是AC和BD的中点,则MN的长度 .
在?ABCD中,AE平分∠BAD交BC于点E,点E将BC分为4和3两部分,则?ABCD的周长为 .
如图,在?ABCD中,点E是CD边的中点,连接AE并延长交BC的延长线于点F,连接BE,BE⊥AF.
(1)求证:AE平分∠DAB;
(2)若∠DAB=60°,AB=4,求?ABCD的面积.
22.已知:如图,在?ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.求证:BD、EF互相平分.
23.如图,四边形ACFD是平行四边形,B,E,C,F在一条直线上,已知BE=CF.
(1)求证:四边形ABED是平行四边形.
(2)若∠ABC=60°,且AC⊥BF,AB=6,BF=5,求AD的长.
24.如图,分别以Rt△ACB的直角边AC和斜边AB向外作等边△ACE,等边△ABD,取AB的中点F,连接DF、EF,已知∠BAC=30°.
(1)求证:四边形ADFE是平行四边形;
(2)若BD=4,求四边形BCEF的面积.
25.如图,已知四边形ABCD是平行四边形,E是AB延长线上一点且BE=AB,连接CE,BD.
(1)求证:四边形BECD是平行四边形;
(2)连接DE,若AB=BD=4,DE=2,求平行四边形BECD的面积.
26.如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
27.【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.
【结论应用】
(1)如图②,在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F.求证:∠AEN=∠F.
(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为 .
28.已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.
参考答案
1.解:A、在?ABCD中,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=CE,
∴四边形AECF是平行四边形,
∴AE=CF,
故A可以使AE=CF,不符合题意;
B、∵AE∥CF,AF∥CE,
∴四边形AECF是平行四边形,
∴AE=CF,
故B可以使AE=CF,不符合题意;
C、添加AE=AF后不能使AE=CF,
故C符合题意;
D、∵四边形AECF是平行四边形,
∴AE=CF,
故D可以使AE=CF,不符合题意;
故选:C.
2.解:连接AC,取AC的中点H,连接MH、NH,
∵M、H分别是AD、AC的中点,
∴MH=CD=2,
同理可得,NH=AB=,
在△MHN中,MH﹣NH<MN<MH+NH,即<MN<,
当点H在MN上时,MN=MH+NH=,
∴<MN≤,
故选:D.
3.解:∵?ABCD的周长是36cm,
∴AB+AD=18m,
∵△ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=(AB+BC+AC)﹣(AB+AC)=28﹣18=10(cm).
故选:C.
4.解:连接DN、DB,
在Rt△DAB中,∠A=90°,AB=2,AD=2,
∴BD==4,
∵点E,F分别为DM,MN的中点,
∴EF=DN,
由题意得,当点N与点B重合是DN最大,最大值为4,
∴EF长度的最大值为2,
故选:D.
5.解:∵四边形ABCD是平行四边形,
∴∠A+∠B=180°,
∵∠A﹣∠B=20°,
∴∠A=100°,
∴∠C=∠A=100°.
故选:C.
6.解:连接DE,连接并延长EP交BC于点F,
∵DE是△ABC中位线,
∴DE=BC,AE=BE,AD=CD,
∴∠EDB=∠DBF,
∵P、Q是BD、CE的中点,
∴DP=BP,
∵在△DEP与△BFP中,
,
∴△DEP≌△BFP(ASA),
∴BF=DE=BC,P是EF中点,
∴FC=BC,
PQ是△EFC中位线,
PQ=FC,
∴PQ:BC=1:4.
故选:A.
7.解:当点F在C的左侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BC﹣BF=(8﹣3t)cm,
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=8﹣3t,
解得:t=2;
当点F在C的右侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BF﹣BC=(3t﹣8)cm,
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=3t﹣8,
解得:t=4;
综上可得:当t=2或4s时,以A、C、E、F为顶点四边形是平行四边形,
故选:D.
8.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AD∥EF,CD∥GH,
∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个.
即共有9个平行四边形,
故选:D.
9.解:∵BD=BC,
∴∠BDC=∠C=50°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BDC=∠ABE=50°,
∵AE⊥BD,
∴∠AEB=90°,
∴∠EAB=90°﹣50°=40°.
故答案为:40°.
10.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠D=102°,AD=BC,
∵AD=AE=BE,
∴BC=AE=BE,
∴∠EAB=∠EBA,∠BEC=∠ECB,
∵∠BEC=∠EAB+∠EBA=2∠EAB,
∴∠ACB=2∠CAB,
∴∠CAB+∠ACB=3∠CAB=180°﹣∠ABC=180°﹣102°,
∴∠BAC=26°,
故答案为:26°.
11.解:∵点O是BD中点,EO⊥BD,
∴EO是线段BD的中垂线,
∴BE=ED,
∴△ABE的周长=AB+AD,
又∵平行四边形的周长为12cm,
∴AB+AD=6(cm).
故答案为:6cm.
12.解:设运动了x秒.
根据题意有AP=xcm,CQ=2xcm,PD=(8﹣x)cm,
∵AD∥BC,
∴当PD=CQ时,四边形PQCD是平行四边形,
∴8﹣x=2x,
解得:x=,
∴s时,四边形PDCQ是平行四边形,
故答案为:.
13.解:如图,
以BC为对角线,将AB向上平移3个单位,再向左平移1个单位,B点对应的位置为(﹣2,3)就是第四个顶点D1;
以AB为对角线,将BC向下平移3个单位,再向右平移1个单位,B点对应的位置为(0,﹣3)就是第四个顶点D2′;
以AC为对角线,将AB向上平移3个单位,再向右平移4个单位,C点对应的位置为(7,3)就是第四个顶点D3;
∴第四个顶点D的坐标为:(﹣2,3)或(0,﹣3)或(7,3),
故答案为:(﹣2,3)或(0,﹣3)或(7,3).
14.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,OB=OD,
又平行四边形ABCD的周长为60cm,△AOB的周长比△BOC的周长长8cm,
∴,
两个方程相加,得AB=19(cm).
故答案为:19.
15.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
16.解:延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA)
∴AD=AB=10,BN=ND,
∵BN=ND,BM=MC,
∴CD=2MN=6,
∴AC=AD+CD=16,
故答案为:16.
17.解:∵AE⊥BC,AF⊥CD,
∴∠AEC=∠AFC=90°,
在四边形AECF中,∠C=360°﹣∠EAF﹣∠AEC﹣∠AFC=360°﹣70°﹣90°﹣90°=110°,
在?ABCD中,∠B=180°﹣∠C=180°﹣110°=70°.
故答案为:70°.
18.解:设两个阴影部分三角形的底为AB,CD,高分别为h1,h2,则h1+h2为平行四边形的高,
∴S△EAB+S△ECD=AB?h1+CD?h2=AB(h1+h2)
=S四边形ABCD=×6=3.
故答案为:3.
19.解:延长DM交AB于E,
∵AB∥CD,
∴∠C=∠A,
在△AME和△CMD中,
,
∴△AME≌△CMD(ASA)
∴AE=CD=3,DM=ME,
∴BE=AB﹣AE=4,
∵DM=ME,DN=NB,
∴MN是△DEB的中位线,
∴MN=BE=2,
故答案为:2.
20.解:∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵?ABCD的边AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
①当BE=4时,AB=4,BC=4+3=7,
?ABCD的周长=2(AB+BC)=2(4+7)=22,
②当BE=3时,AB=3,BC=3+4=7,
?ABCD的周长=2(AB+BC)=2(3+7)=20,
所以,?ABCD的周长为22或20.
故答案为:22或20.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠EFC,
∵点E是CD边的中点,
∴DE=CE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴AE=FE,
∵BE⊥AF.
∴BA=BF,
∴∠BAF=∠BFA,
∵∠DAE=∠BFA,
∴∠DAE=∠BAF,
∴AE平分∠DAB;
(2)∵∠DAB=60°,AB=4,
∴∠DAE=∠BAF=30°,
∵BE⊥AF.
∴BE=AB=2,
∴AE=BE=2,
∵△ADE≌△FCE,
∴△ADE的面积=△FCE的面积,
∴?ABCD的面积=△ABF的面积=2△ABE的面积=2××AE?BE=2×2=4.
22.证明:连接BE、DF,如图所示:
∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
又∵AE=CF,
∴DE=BF,
∴四边形EBFD为平行四边形,
∴BD、EF互相平分.
23.证明:(1)∵四边形ACFD是平行四边形,
∴AD∥CF,AD=CF,
∵B,E,C,F在一条直线上,
∴AD∥BE,
∵BE=CF.
∴AD=BE,
∴四边形ABED是平行四边形;
(2)∵四边形ACFD是平行四边形,
∴AD=CF,
∵∠ABC=60°,且AC⊥BF,AB=6,
∴∠BAC=30°,
∴BC=AB=3,
∵BF=5,
∴CF=BF﹣BC=2,
∴AD=2.
24.(1)证明:∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABD是等边三角形,F是AB的中点,
∴AD=AB=BD,AB=2AF,DF⊥AB,
∴AF=BC,
在Rt△AFD和Rt△BCA中,
,
∴Rt△AFD≌Rt△BCA(HL),
∴DF=AC,
∵△ACE是等边三角形,
∴∠EAC=60°,AC=AE,
∴∠EAB=∠EAC+∠BAC=90°,
∴DF=AE,
又∵DF⊥AB,
∴DF∥AE,
∴四边形ADFE是平行四边形;
(2)解:由(1)得:△AEF的面积=△ADF的面积=△ABC的面积,AB=BD=4,BC=AB=2,AC=BC=2,
∴四边形BCEF的面积=△ACE的面积+△ABC的面积﹣△AEF的面积=△ACE的面积=×(2)2=3.
25.(1)证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AE,
∵AB=BE,
∴CD=BE,CD∥BE,
∴四边形BECD是平行四边形;
(2)解:过D作DH⊥AE于H,
∵AB=BD=4,
∴BE=AB=4,
∴BD2﹣BH2=DE2﹣EH2=DH2,
∴42﹣BH2=(2)2﹣(4﹣BH)2,
∴BH=3,
∴DH===,
∴平行四边形BECD的面积=BE?DH=4×=4.
26.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(ASA),
∴DF=CF,
又∵AF=EF,
∴四边形ACED是平行四边形.
27.【教材呈现】证明:∵P是BD的中点,M是DC的中点,
∴PM=BC,
同理,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM,
【结论应用】(1)证明:∵P是BD的中点,M是DC的中点,
∴PM∥BC,
∴∠PMN=∠F,
同理,∠PNM=∠AEN,
∵∠PMN=∠PNM,
∴∠AEN=∠F;
(2)解:∵PN∥AD,
∴∠PNB=∠A,
∵∠DPN是△PNB的一个外角,
∴∠DPN=∠PNB+∠ABD=∠A+∠ABD,
∵PM∥BC,
∴∠MPD=∠DBC,
∴∠MPN=∠DPN+∠MPD=∠A+∠ABD+∠DBC=∠A+∠ABC=122°,
∵PM=PN,
∴∠PMN=×(180°﹣122°)=29°,
∴∠F=∠PMN=29°,
故答案为:29°.
28.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,
∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB﹣AE=CD﹣CF 即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形.
∴BD、EF互相平分;
(2)∵∠A=60°,AE=AD,
∴△ADE是等边三角形,
∵AD=4,
∴DE=AE=4,
∵AE=2EB,
∴BE=GE=2,
∴BG=4,
过D点作DG⊥AB于点G,
在Rt△ADG中,AD=4,∠A=60°,
∴AG=AD=2,
∴DG==2,
∴BD===2.
1.如图,平行四边形ABCD中,E、F分别在边BC、AD上,添加条件后不能使AE=CF的是( )
A.BE=DF B.AE∥CF
C.AF=AE D.四边形AECF为平行四边形
2.如图,四边形ABCD中,AB=1,CD=4,M、N分别是AD、BC的中点,则线段MN的取值范围是( )
A.3<MN<5 B.3<MN≤5 C.<MN< D.<MN≤
3.如图,?ABCD的周长为36cm,△ABC的周长为28cm,则对角线AC的长为( )
A.28cm B.18cm C.10cm D.8cm
4.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3 B.2 C.4 D.2
5.在?ABCD中,已知∠A﹣∠B=20°,则∠C=( )
A.60° B.80° C.100° D.120°
6.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
A.1:4 B.1:5 C.1:6 D.1:7
7.如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以3cm/s的速度运动,E、F同时出发.设运动时间为t(s),当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A.1或2 B.2 C.2或3 D.2或4
8.如图,在平行四边形ABCD中,如果EF∥AD,GH∥CD,EF与GH相交于点O,那么图中的平行四边形一共有( )
A.4个 B.5个 C.8个 D.9个
9.如图,在平行四边形ABCD中,BD=BC,AE⊥BD,垂足为E,若∠C=50°,则∠EAB的度数为 .
10.如图,AC是?ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的度数是 .
11.如图,在周长为12cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,则△ABE的周长为 .
12.如图,在四边形ABCD中,AD∥BC,且AD=8cm,BC=6cm,点P、Q分别从点A、C同时出发,点P以1cm/s的速度由点A向点D运动,点Q以2cm/s的速度由点C向点B运动,当点P、Q中有一点到达终点时,另一点也随之停止运动,则 s后四边形PQCD是平行四边形.
13.已知点A(3,0)、B(﹣1,0)、C(2,3),以A、B、C为顶点画平行四边形,则第四个顶点D的坐标是 .
14.?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,则AB的长为 cm.
15.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是 .
16.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=10cm,MN=3cm,则AC的长为 cm
17.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=70°,则∠B的度数为 .
18.如图,E为?ABCD内任一点,且?ABCD的面积为6,则图中阴影部分的面积为 .
19.如图,AB∥CD,AB=7,CD=3,M、N分别是AC和BD的中点,则MN的长度 .
在?ABCD中,AE平分∠BAD交BC于点E,点E将BC分为4和3两部分,则?ABCD的周长为 .
如图,在?ABCD中,点E是CD边的中点,连接AE并延长交BC的延长线于点F,连接BE,BE⊥AF.
(1)求证:AE平分∠DAB;
(2)若∠DAB=60°,AB=4,求?ABCD的面积.
22.已知:如图,在?ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.求证:BD、EF互相平分.
23.如图,四边形ACFD是平行四边形,B,E,C,F在一条直线上,已知BE=CF.
(1)求证:四边形ABED是平行四边形.
(2)若∠ABC=60°,且AC⊥BF,AB=6,BF=5,求AD的长.
24.如图,分别以Rt△ACB的直角边AC和斜边AB向外作等边△ACE,等边△ABD,取AB的中点F,连接DF、EF,已知∠BAC=30°.
(1)求证:四边形ADFE是平行四边形;
(2)若BD=4,求四边形BCEF的面积.
25.如图,已知四边形ABCD是平行四边形,E是AB延长线上一点且BE=AB,连接CE,BD.
(1)求证:四边形BECD是平行四边形;
(2)连接DE,若AB=BD=4,DE=2,求平行四边形BECD的面积.
26.如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
27.【教材呈现】
如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.
【结论应用】
(1)如图②,在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F.求证:∠AEN=∠F.
(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为 .
28.已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.
参考答案
1.解:A、在?ABCD中,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=CE,
∴四边形AECF是平行四边形,
∴AE=CF,
故A可以使AE=CF,不符合题意;
B、∵AE∥CF,AF∥CE,
∴四边形AECF是平行四边形,
∴AE=CF,
故B可以使AE=CF,不符合题意;
C、添加AE=AF后不能使AE=CF,
故C符合题意;
D、∵四边形AECF是平行四边形,
∴AE=CF,
故D可以使AE=CF,不符合题意;
故选:C.
2.解:连接AC,取AC的中点H,连接MH、NH,
∵M、H分别是AD、AC的中点,
∴MH=CD=2,
同理可得,NH=AB=,
在△MHN中,MH﹣NH<MN<MH+NH,即<MN<,
当点H在MN上时,MN=MH+NH=,
∴<MN≤,
故选:D.
3.解:∵?ABCD的周长是36cm,
∴AB+AD=18m,
∵△ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=(AB+BC+AC)﹣(AB+AC)=28﹣18=10(cm).
故选:C.
4.解:连接DN、DB,
在Rt△DAB中,∠A=90°,AB=2,AD=2,
∴BD==4,
∵点E,F分别为DM,MN的中点,
∴EF=DN,
由题意得,当点N与点B重合是DN最大,最大值为4,
∴EF长度的最大值为2,
故选:D.
5.解:∵四边形ABCD是平行四边形,
∴∠A+∠B=180°,
∵∠A﹣∠B=20°,
∴∠A=100°,
∴∠C=∠A=100°.
故选:C.
6.解:连接DE,连接并延长EP交BC于点F,
∵DE是△ABC中位线,
∴DE=BC,AE=BE,AD=CD,
∴∠EDB=∠DBF,
∵P、Q是BD、CE的中点,
∴DP=BP,
∵在△DEP与△BFP中,
,
∴△DEP≌△BFP(ASA),
∴BF=DE=BC,P是EF中点,
∴FC=BC,
PQ是△EFC中位线,
PQ=FC,
∴PQ:BC=1:4.
故选:A.
7.解:当点F在C的左侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BC﹣BF=(8﹣3t)cm,
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=8﹣3t,
解得:t=2;
当点F在C的右侧时,根据题意得:AE=tcm,BF=3tcm,
则CF=BF﹣BC=(3t﹣8)cm,
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=3t﹣8,
解得:t=4;
综上可得:当t=2或4s时,以A、C、E、F为顶点四边形是平行四边形,
故选:D.
8.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AD∥EF,CD∥GH,
∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个.
即共有9个平行四边形,
故选:D.
9.解:∵BD=BC,
∴∠BDC=∠C=50°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BDC=∠ABE=50°,
∵AE⊥BD,
∴∠AEB=90°,
∴∠EAB=90°﹣50°=40°.
故答案为:40°.
10.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠D=102°,AD=BC,
∵AD=AE=BE,
∴BC=AE=BE,
∴∠EAB=∠EBA,∠BEC=∠ECB,
∵∠BEC=∠EAB+∠EBA=2∠EAB,
∴∠ACB=2∠CAB,
∴∠CAB+∠ACB=3∠CAB=180°﹣∠ABC=180°﹣102°,
∴∠BAC=26°,
故答案为:26°.
11.解:∵点O是BD中点,EO⊥BD,
∴EO是线段BD的中垂线,
∴BE=ED,
∴△ABE的周长=AB+AD,
又∵平行四边形的周长为12cm,
∴AB+AD=6(cm).
故答案为:6cm.
12.解:设运动了x秒.
根据题意有AP=xcm,CQ=2xcm,PD=(8﹣x)cm,
∵AD∥BC,
∴当PD=CQ时,四边形PQCD是平行四边形,
∴8﹣x=2x,
解得:x=,
∴s时,四边形PDCQ是平行四边形,
故答案为:.
13.解:如图,
以BC为对角线,将AB向上平移3个单位,再向左平移1个单位,B点对应的位置为(﹣2,3)就是第四个顶点D1;
以AB为对角线,将BC向下平移3个单位,再向右平移1个单位,B点对应的位置为(0,﹣3)就是第四个顶点D2′;
以AC为对角线,将AB向上平移3个单位,再向右平移4个单位,C点对应的位置为(7,3)就是第四个顶点D3;
∴第四个顶点D的坐标为:(﹣2,3)或(0,﹣3)或(7,3),
故答案为:(﹣2,3)或(0,﹣3)或(7,3).
14.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,OB=OD,
又平行四边形ABCD的周长为60cm,△AOB的周长比△BOC的周长长8cm,
∴,
两个方程相加,得AB=19(cm).
故答案为:19.
15.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
16.解:延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA)
∴AD=AB=10,BN=ND,
∵BN=ND,BM=MC,
∴CD=2MN=6,
∴AC=AD+CD=16,
故答案为:16.
17.解:∵AE⊥BC,AF⊥CD,
∴∠AEC=∠AFC=90°,
在四边形AECF中,∠C=360°﹣∠EAF﹣∠AEC﹣∠AFC=360°﹣70°﹣90°﹣90°=110°,
在?ABCD中,∠B=180°﹣∠C=180°﹣110°=70°.
故答案为:70°.
18.解:设两个阴影部分三角形的底为AB,CD,高分别为h1,h2,则h1+h2为平行四边形的高,
∴S△EAB+S△ECD=AB?h1+CD?h2=AB(h1+h2)
=S四边形ABCD=×6=3.
故答案为:3.
19.解:延长DM交AB于E,
∵AB∥CD,
∴∠C=∠A,
在△AME和△CMD中,
,
∴△AME≌△CMD(ASA)
∴AE=CD=3,DM=ME,
∴BE=AB﹣AE=4,
∵DM=ME,DN=NB,
∴MN是△DEB的中位线,
∴MN=BE=2,
故答案为:2.
20.解:∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵?ABCD的边AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
①当BE=4时,AB=4,BC=4+3=7,
?ABCD的周长=2(AB+BC)=2(4+7)=22,
②当BE=3时,AB=3,BC=3+4=7,
?ABCD的周长=2(AB+BC)=2(3+7)=20,
所以,?ABCD的周长为22或20.
故答案为:22或20.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠EFC,
∵点E是CD边的中点,
∴DE=CE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴AE=FE,
∵BE⊥AF.
∴BA=BF,
∴∠BAF=∠BFA,
∵∠DAE=∠BFA,
∴∠DAE=∠BAF,
∴AE平分∠DAB;
(2)∵∠DAB=60°,AB=4,
∴∠DAE=∠BAF=30°,
∵BE⊥AF.
∴BE=AB=2,
∴AE=BE=2,
∵△ADE≌△FCE,
∴△ADE的面积=△FCE的面积,
∴?ABCD的面积=△ABF的面积=2△ABE的面积=2××AE?BE=2×2=4.
22.证明:连接BE、DF,如图所示:
∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
又∵AE=CF,
∴DE=BF,
∴四边形EBFD为平行四边形,
∴BD、EF互相平分.
23.证明:(1)∵四边形ACFD是平行四边形,
∴AD∥CF,AD=CF,
∵B,E,C,F在一条直线上,
∴AD∥BE,
∵BE=CF.
∴AD=BE,
∴四边形ABED是平行四边形;
(2)∵四边形ACFD是平行四边形,
∴AD=CF,
∵∠ABC=60°,且AC⊥BF,AB=6,
∴∠BAC=30°,
∴BC=AB=3,
∵BF=5,
∴CF=BF﹣BC=2,
∴AD=2.
24.(1)证明:∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABD是等边三角形,F是AB的中点,
∴AD=AB=BD,AB=2AF,DF⊥AB,
∴AF=BC,
在Rt△AFD和Rt△BCA中,
,
∴Rt△AFD≌Rt△BCA(HL),
∴DF=AC,
∵△ACE是等边三角形,
∴∠EAC=60°,AC=AE,
∴∠EAB=∠EAC+∠BAC=90°,
∴DF=AE,
又∵DF⊥AB,
∴DF∥AE,
∴四边形ADFE是平行四边形;
(2)解:由(1)得:△AEF的面积=△ADF的面积=△ABC的面积,AB=BD=4,BC=AB=2,AC=BC=2,
∴四边形BCEF的面积=△ACE的面积+△ABC的面积﹣△AEF的面积=△ACE的面积=×(2)2=3.
25.(1)证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AE,
∵AB=BE,
∴CD=BE,CD∥BE,
∴四边形BECD是平行四边形;
(2)解:过D作DH⊥AE于H,
∵AB=BD=4,
∴BE=AB=4,
∴BD2﹣BH2=DE2﹣EH2=DH2,
∴42﹣BH2=(2)2﹣(4﹣BH)2,
∴BH=3,
∴DH===,
∴平行四边形BECD的面积=BE?DH=4×=4.
26.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(ASA),
∴DF=CF,
又∵AF=EF,
∴四边形ACED是平行四边形.
27.【教材呈现】证明:∵P是BD的中点,M是DC的中点,
∴PM=BC,
同理,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM,
【结论应用】(1)证明:∵P是BD的中点,M是DC的中点,
∴PM∥BC,
∴∠PMN=∠F,
同理,∠PNM=∠AEN,
∵∠PMN=∠PNM,
∴∠AEN=∠F;
(2)解:∵PN∥AD,
∴∠PNB=∠A,
∵∠DPN是△PNB的一个外角,
∴∠DPN=∠PNB+∠ABD=∠A+∠ABD,
∵PM∥BC,
∴∠MPD=∠DBC,
∴∠MPN=∠DPN+∠MPD=∠A+∠ABD+∠DBC=∠A+∠ABC=122°,
∵PM=PN,
∴∠PMN=×(180°﹣122°)=29°,
∴∠F=∠PMN=29°,
故答案为:29°.
28.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,
∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB﹣AE=CD﹣CF 即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形.
∴BD、EF互相平分;
(2)∵∠A=60°,AE=AD,
∴△ADE是等边三角形,
∵AD=4,
∴DE=AE=4,
∵AE=2EB,
∴BE=GE=2,
∴BG=4,
过D点作DG⊥AB于点G,
在Rt△ADG中,AD=4,∠A=60°,
∴AG=AD=2,
∴DG==2,
∴BD===2.
