第16章二次根式 单元综合提升-2020-2021学年人教版八年级数学下册(word版含解析)
文档属性
| 名称 | 第16章二次根式 单元综合提升-2020-2021学年人教版八年级数学下册(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 330.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 00:00:00 | ||
图片预览



文档简介
2020-2021年人教版八年级数学下册《第16章二次根式》单元综合同步提升训练(附答案)
1.a=2019×2021﹣2019×2020,b=,c=,则a,b,c的大小关系是( )
A.a<b<c B.a<c<b C.b<a<c D.b<c<a
2.如图,从一个大正方形中裁去面积为16cm2和24cm2的两个小正方形,则余下的面积为( )
A.16cm2 B.40 cm2 C.8cm2 D.(2+4)cm2
3.若二次根式有意义,且关于x的分式方程有正数解,则符合条件的整数m的和是( )
A.﹣7 B.﹣6 C.﹣5 D.﹣4
4.下列计算正确的是( )
A.=2 B.+= C.×= D.÷=2
5.已知:a=,b=,则a与b的关系是( )
A.a﹣b=0 B.a+b=0 C.ab=1 D.a2=b2
6.把根号外的因式移入根号内得( )
A. B. C. D.
7.化简﹣a的结果是( )
A.﹣2a B.﹣2a C.0 D.2a
8.在△ABC中,a、b、c为三角形的三边,化简﹣2|c﹣a﹣b|的结果为( )
A.3a+b﹣c B.﹣a﹣3b+3c C.a+3b﹣c D.2a
一个直角三角形的两直角边长分别为cm和cm,则这个直角三角形的
面积是 cm2.
10.若,则m的取值范围是 .
11.计算(2﹣)2的结果等于 .
12.已知xy>0,则化简代数式x的结果是 .
13.式子在实数范围内有意义,则x的范围是 .
14.已知a=3+,b=3﹣,则a2b+ab2= .
15.已知a+b=﹣2,ab=1,则= .
16.如图,在长方形内有两个相邻的正方形A,B,正方形A的面积为2,正方形B的面积为4,则图中阴影部分的面积是 .
17.当﹣1<a<0时,则= .
18.计算:6×= ,÷(2﹣)= .
19.=2,=3,=4,…观察下列各式:请你找出其中规律,并将第n(n≥1)个等式写出来 .
20.若x=﹣1,则x3+x2﹣3x+2021的值为 .
21.化简求值:已知:x=,y=,求(x+3)(y+3)的值.
22.已知x+y=﹣5,xy=6,求+的值.
23.计算:(x>0).
24.(﹣2)4+()2﹣(﹣)(+)÷.
25.计算:
(1)÷﹣×+
(2)(3+2)(3﹣2)﹣(﹣)2.
26.先化简,再求值:已知a=8,b=2,试求a+﹣+的值.
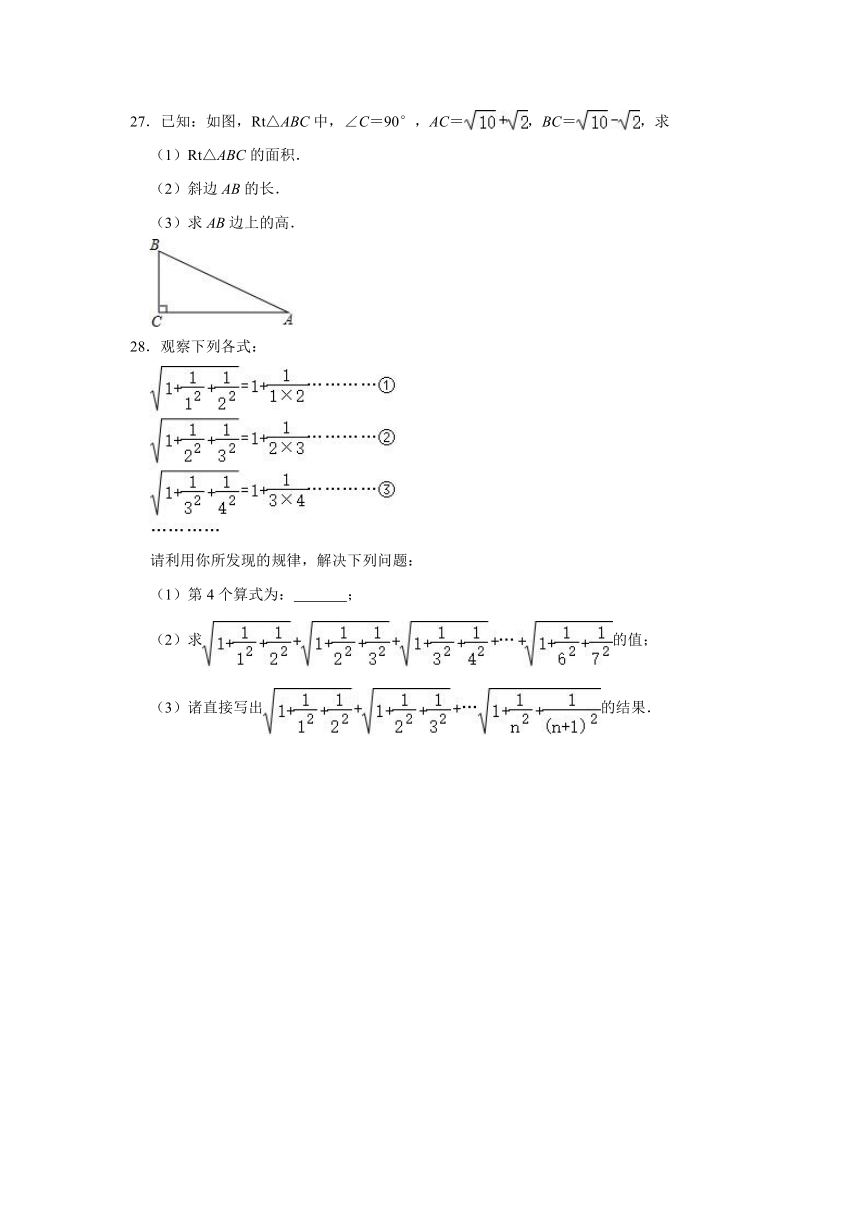
27.已知:如图,Rt△ABC中,∠C=90°,AC=,BC=,求
(1)Rt△ABC的面积.
(2)斜边AB的长.
(3)求AB边上的高.
28.观察下列各式:
请利用你所发现的规律,解决下列问题:
(1)第4个算式为: ;
(2)求的值;
(3)诸直接写出的结果.
参考答案
1.解:a=2019×2021﹣2019×2020=2019(2021﹣2020)=2019;
∵20222﹣4×2021=(2021+1)2﹣4×2021=20212+2×2021+1﹣4×2021
=20212﹣2×2021+1=(2021﹣1)2=20202,
∴b=2020;
∵>,
∴c>b>a.
故选:A.
2.解:从一个大正方形中裁去面积为16cm2和24cm2的两个小正方形,
大正方形的边长是+=4+2,
留下部分(即阴影部分)的面积是(4+2)2﹣16﹣24=16+16+24﹣16﹣24=16(cm2).
故选:A.
3.解:去分母得,﹣m+2(x﹣1)=3,
解得,x=,
∵关于x的分式方程有正数解,
∴>0,
∴m>﹣5,
又∵x=1是增根,当x=1时,=1,即m=﹣3
∴m≠﹣3,
∵有意义,
∴2﹣m≥0,
∴m≤2,
因此﹣5<m≤2且m≠﹣3,
∵m为整数,
∴m可以为﹣4,﹣2,﹣1,0,1,2,其和为﹣4,
故选:D.
4.解:A.=2,此选项错误;
B.与不是同类二次根式,不能合并,此选项错误;
C.×=,此选项正确;
D.÷=,此选项错误;
故选:C.
5.解:分母有理化,可得a=2+,b=2﹣,
∴a﹣b=(2+)﹣(2﹣)=2,故A选项错误;
a+b=(2+)+(2﹣)=4,故B选项错误;
ab=(2+)×(2﹣)=4﹣3=1,故C选项正确;
∵a2=(2+)2=4+4+3=7+4,b2=(2﹣)2=4﹣4+3=7﹣4,
∴a2≠b2,故D选项错误;
故选:C.
6.解:∵成立,
∴﹣>0,即m<0,
∴原式=﹣=﹣.
故选:D.
7.解:﹣a=﹣a﹣a2?=﹣a+a=0.
故选:C.
8.解:∵a、b、c为三角形的三边,
∴a+c>b,a+b>c,
即a﹣b+c>0,c﹣a﹣b<0;
∴﹣2|c﹣a﹣b|=(a﹣b+c)+2(c﹣a﹣b)=﹣a﹣3b+3c.
故选:B.
9.解:这个直角三角形的面积=cm2,
故答案为:2
10.解:,得4﹣m≥0,
解得m≤4,
故答案为:m≤4.
11.解:原式=20﹣4+2=22﹣4.
故答案为22﹣4.
12.解:∵xy>0,且有意义,
∴x<0,y<0,
∴x=x?=﹣.
故答案为:﹣.
13.解:∵式子在实数范围内有意义,
∴,解得x≥1且x≠2.
故答案为:x≥1且x≠2.
14.解:∵a=3+,b=3﹣,
∴a2b+ab2=ab(a+b)=(3+2)(3﹣2)(3+2+3﹣2)=6;
故答案为:6.
15.解:∵=++2,=+2,=(a+b)2﹣2ab+2,=4,
∴=2.
故答案为:2.
16.解:设两个正方形A,B的边长是x、y(x<y),
则x2=2,y2=4,
x=,y=2,
则阴影部分的面积是(y﹣x)x=(2﹣)×=2﹣2,
故答案为:2﹣2.
17.解:∵﹣1<a<0,
∴a+<0,a﹣>0,
原式=﹣=a﹣+a+=2a,
故答案为:2a.
18.解:6×=2=4,
÷(2﹣)====+1,
故答案为:4,+1.
19.解:由=2,=3,=4,…得
=(n+1),
故答案为:=(n+1).
20.解:∵x=﹣1,
∴x2=(﹣1)2=2﹣2+1=3﹣2,
则原式=x?x2+x2﹣3x+2021
=(﹣1)×(3﹣2)+3﹣2﹣3(﹣1)+2021
=3﹣4﹣3+2+3﹣2﹣3+3+2021=2020,
故答案为:2020.
21.解:当x===,
y===时,
原式=xy+3x+3y+9=xy+3(x+y)+9
=×+3×(+)+9
=+3×+9=+3+9=+3.
22.解:∵x+y=﹣5,xy=6,
∴x<0,y<0,
∴+=﹣()=﹣=﹣,
∵x+y=﹣5,xy=6,
∴﹣=﹣=.
23.解:∵x>0,xy3≥0,
∴y≥0,
∴原式=?(﹣)?(﹣)
=﹣?(﹣)=﹣xy?(﹣x)=.
24.解:原式=16++3÷3=.
25.解:(1)原式=﹣+2=4﹣+2=4+;
(2)原式=18﹣12﹣(3﹣2+2)=6﹣5+2=1+2.
26.解:a+﹣+=+2﹣+=+3
当a=8,b=2时,
原式=+3=+3=4
27.解:(1)∵Rt△ABC中,∠C=90°,AC=,BC=,
∴Rt△ABC的面积===4,
即Rt△ABC的面积是4;
(2)∵Rt△ABC中,∠C=90°,AC=,BC=,
∴AB===2,
即AB的长是2;
(3)∵Rt△ABC的面积是4,AB=2,
∴AB边上的高是:=,
即AB边上的高是.
28.解:
(1)依题意:接下来的第4个算式为:
故答案为
(2)原式=
===
(3)
原式=
===
1.a=2019×2021﹣2019×2020,b=,c=,则a,b,c的大小关系是( )
A.a<b<c B.a<c<b C.b<a<c D.b<c<a
2.如图,从一个大正方形中裁去面积为16cm2和24cm2的两个小正方形,则余下的面积为( )
A.16cm2 B.40 cm2 C.8cm2 D.(2+4)cm2
3.若二次根式有意义,且关于x的分式方程有正数解,则符合条件的整数m的和是( )
A.﹣7 B.﹣6 C.﹣5 D.﹣4
4.下列计算正确的是( )
A.=2 B.+= C.×= D.÷=2
5.已知:a=,b=,则a与b的关系是( )
A.a﹣b=0 B.a+b=0 C.ab=1 D.a2=b2
6.把根号外的因式移入根号内得( )
A. B. C. D.
7.化简﹣a的结果是( )
A.﹣2a B.﹣2a C.0 D.2a
8.在△ABC中,a、b、c为三角形的三边,化简﹣2|c﹣a﹣b|的结果为( )
A.3a+b﹣c B.﹣a﹣3b+3c C.a+3b﹣c D.2a
一个直角三角形的两直角边长分别为cm和cm,则这个直角三角形的
面积是 cm2.
10.若,则m的取值范围是 .
11.计算(2﹣)2的结果等于 .
12.已知xy>0,则化简代数式x的结果是 .
13.式子在实数范围内有意义,则x的范围是 .
14.已知a=3+,b=3﹣,则a2b+ab2= .
15.已知a+b=﹣2,ab=1,则= .
16.如图,在长方形内有两个相邻的正方形A,B,正方形A的面积为2,正方形B的面积为4,则图中阴影部分的面积是 .
17.当﹣1<a<0时,则= .
18.计算:6×= ,÷(2﹣)= .
19.=2,=3,=4,…观察下列各式:请你找出其中规律,并将第n(n≥1)个等式写出来 .
20.若x=﹣1,则x3+x2﹣3x+2021的值为 .
21.化简求值:已知:x=,y=,求(x+3)(y+3)的值.
22.已知x+y=﹣5,xy=6,求+的值.
23.计算:(x>0).
24.(﹣2)4+()2﹣(﹣)(+)÷.
25.计算:
(1)÷﹣×+
(2)(3+2)(3﹣2)﹣(﹣)2.
26.先化简,再求值:已知a=8,b=2,试求a+﹣+的值.
27.已知:如图,Rt△ABC中,∠C=90°,AC=,BC=,求
(1)Rt△ABC的面积.
(2)斜边AB的长.
(3)求AB边上的高.
28.观察下列各式:
请利用你所发现的规律,解决下列问题:
(1)第4个算式为: ;
(2)求的值;
(3)诸直接写出的结果.
参考答案
1.解:a=2019×2021﹣2019×2020=2019(2021﹣2020)=2019;
∵20222﹣4×2021=(2021+1)2﹣4×2021=20212+2×2021+1﹣4×2021
=20212﹣2×2021+1=(2021﹣1)2=20202,
∴b=2020;
∵>,
∴c>b>a.
故选:A.
2.解:从一个大正方形中裁去面积为16cm2和24cm2的两个小正方形,
大正方形的边长是+=4+2,
留下部分(即阴影部分)的面积是(4+2)2﹣16﹣24=16+16+24﹣16﹣24=16(cm2).
故选:A.
3.解:去分母得,﹣m+2(x﹣1)=3,
解得,x=,
∵关于x的分式方程有正数解,
∴>0,
∴m>﹣5,
又∵x=1是增根,当x=1时,=1,即m=﹣3
∴m≠﹣3,
∵有意义,
∴2﹣m≥0,
∴m≤2,
因此﹣5<m≤2且m≠﹣3,
∵m为整数,
∴m可以为﹣4,﹣2,﹣1,0,1,2,其和为﹣4,
故选:D.
4.解:A.=2,此选项错误;
B.与不是同类二次根式,不能合并,此选项错误;
C.×=,此选项正确;
D.÷=,此选项错误;
故选:C.
5.解:分母有理化,可得a=2+,b=2﹣,
∴a﹣b=(2+)﹣(2﹣)=2,故A选项错误;
a+b=(2+)+(2﹣)=4,故B选项错误;
ab=(2+)×(2﹣)=4﹣3=1,故C选项正确;
∵a2=(2+)2=4+4+3=7+4,b2=(2﹣)2=4﹣4+3=7﹣4,
∴a2≠b2,故D选项错误;
故选:C.
6.解:∵成立,
∴﹣>0,即m<0,
∴原式=﹣=﹣.
故选:D.
7.解:﹣a=﹣a﹣a2?=﹣a+a=0.
故选:C.
8.解:∵a、b、c为三角形的三边,
∴a+c>b,a+b>c,
即a﹣b+c>0,c﹣a﹣b<0;
∴﹣2|c﹣a﹣b|=(a﹣b+c)+2(c﹣a﹣b)=﹣a﹣3b+3c.
故选:B.
9.解:这个直角三角形的面积=cm2,
故答案为:2
10.解:,得4﹣m≥0,
解得m≤4,
故答案为:m≤4.
11.解:原式=20﹣4+2=22﹣4.
故答案为22﹣4.
12.解:∵xy>0,且有意义,
∴x<0,y<0,
∴x=x?=﹣.
故答案为:﹣.
13.解:∵式子在实数范围内有意义,
∴,解得x≥1且x≠2.
故答案为:x≥1且x≠2.
14.解:∵a=3+,b=3﹣,
∴a2b+ab2=ab(a+b)=(3+2)(3﹣2)(3+2+3﹣2)=6;
故答案为:6.
15.解:∵=++2,=+2,=(a+b)2﹣2ab+2,=4,
∴=2.
故答案为:2.
16.解:设两个正方形A,B的边长是x、y(x<y),
则x2=2,y2=4,
x=,y=2,
则阴影部分的面积是(y﹣x)x=(2﹣)×=2﹣2,
故答案为:2﹣2.
17.解:∵﹣1<a<0,
∴a+<0,a﹣>0,
原式=﹣=a﹣+a+=2a,
故答案为:2a.
18.解:6×=2=4,
÷(2﹣)====+1,
故答案为:4,+1.
19.解:由=2,=3,=4,…得
=(n+1),
故答案为:=(n+1).
20.解:∵x=﹣1,
∴x2=(﹣1)2=2﹣2+1=3﹣2,
则原式=x?x2+x2﹣3x+2021
=(﹣1)×(3﹣2)+3﹣2﹣3(﹣1)+2021
=3﹣4﹣3+2+3﹣2﹣3+3+2021=2020,
故答案为:2020.
21.解:当x===,
y===时,
原式=xy+3x+3y+9=xy+3(x+y)+9
=×+3×(+)+9
=+3×+9=+3+9=+3.
22.解:∵x+y=﹣5,xy=6,
∴x<0,y<0,
∴+=﹣()=﹣=﹣,
∵x+y=﹣5,xy=6,
∴﹣=﹣=.
23.解:∵x>0,xy3≥0,
∴y≥0,
∴原式=?(﹣)?(﹣)
=﹣?(﹣)=﹣xy?(﹣x)=.
24.解:原式=16++3÷3=.
25.解:(1)原式=﹣+2=4﹣+2=4+;
(2)原式=18﹣12﹣(3﹣2+2)=6﹣5+2=1+2.
26.解:a+﹣+=+2﹣+=+3
当a=8,b=2时,
原式=+3=+3=4
27.解:(1)∵Rt△ABC中,∠C=90°,AC=,BC=,
∴Rt△ABC的面积===4,
即Rt△ABC的面积是4;
(2)∵Rt△ABC中,∠C=90°,AC=,BC=,
∴AB===2,
即AB的长是2;
(3)∵Rt△ABC的面积是4,AB=2,
∴AB边上的高是:=,
即AB边上的高是.
28.解:
(1)依题意:接下来的第4个算式为:
故答案为
(2)原式=
===
(3)
原式=
===
