北师大版数学七年级下册:第三章 变量之间的关系 章末练习(word版含解析)
文档属性
| 名称 | 北师大版数学七年级下册:第三章 变量之间的关系 章末练习(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 109.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 10:51:43 | ||
图片预览



文档简介
变量之间的关系 章末练习
1.在三角形ABC中,它的底边是a,底边上的高是h,则三角形面积S=ah,当a为定长时,在此式子中( )
A.S,h是变量,,a是常量
B.S,h,a是变量,是常量
C.a,h是变量,,S是常量
D.S是变量,,a,h是常量
2.小亮帮母亲预算家庭4月份电费开支情况,下表是小亮家4月初连续8天每天早上电表显示的读数:
日期/日
1
2
3
4
5
6
7
8
电表读数/度
21
24
28
33
39
42
46
49
表格中反映的变量是 ,自变量是 ,因变量是 .
3.日常生活中,我们经常要烧开水,下表是对烧水的时间与水的温度的记录:
时间
(分)
1
2
3
4
5
6
7
8
9
10
11
12
13
温度
(℃)
25
29
32
43
52
61
72
81
90
98
100
100
100
(1)上表反映了哪些变量之间的关系?
(2)根据表格的数据判断:在第15分钟时,水的温度为多少?
(3)随着加热时间的增加,水的温度是否会一直上升?
4.如图,一轮船从离A港10千米的P地出发向B港匀速行驶,30分钟后离A港26千米(未到达B港).设x小时后,轮船离A港y千米(未到达B港),则y与x之间的关系式为 .
5.球的体积V与半径R之间的关系式是V=πR3.
(1)在这个式子中,常量、变量分别是什么?
(2)利用这个式子分别求出当球的半径为2 cm,3 cm,4 cm时球的体积;
(3)若R>1,当球的半径增大时,球的体积如何变化?
6.“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用x表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是( )
A B
C D
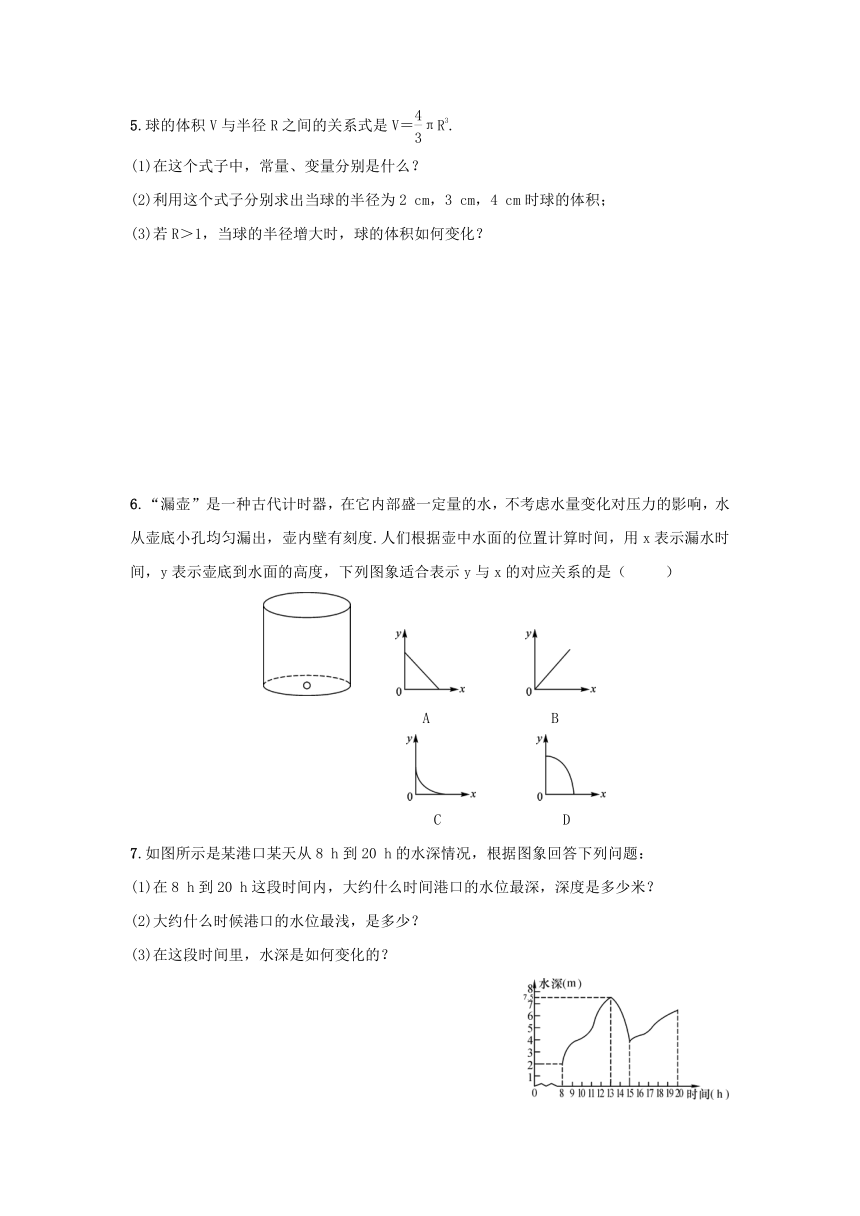
7.如图所示是某港口某天从8 h到20 h的水深情况,根据图象回答下列问题:
(1)在8 h到20 h这段时间内,大约什么时间港口的水位最深,深度是多少米?
(2)大约什么时候港口的水位最浅,是多少?
(3)在这段时间里,水深是如何变化的?
8.小颖画了一个边长为5 cm的正方形,如果将正方形的边长增加x(cm),那么面积的增加值y(cm2)与边长的增加值x(cm)之间的关系式为 .
9.将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度h(cm)与注水时间t(min)的图象大致为图中的( )
10.小明从家出发步行至学校,停留一段时间后乘车返回,则下列图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )
11.一空水池现需注满水,水池深4.9 m,现以不变的流量注水,数据如下表.其中不变的量是 ,可以推断注满水池所需的时间是 .
水的深度h/m
0.7
1.4
2.1
2.8
注水时间t/h
0.5
1
1.5
2
12.如图反映了某出租公司乘车费用y(元)与路程x(千米)之间的关系,请你根据图中信息回答下列问题:
(1)公司规定的起步价是 元;
(2)该公司规定除起步价外,超过5千米的每增加1千米多收 元;
(3)若你是一名乘客,共付了44元钱,则你的行程是 千米.
13.如图1,在直角梯形ABCD中,动点P从点B出发,沿B→C→D→A匀速运动,设点P运动的路程为x,三角形ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 、 ;
(2)当点P运动的路程x=4时,三角形ABP的面积y= ;
(3)求AB的长和梯形ABCD的面积.
14.一游泳池长90 m,甲、乙两人分别从两对边同时向所对的另一边游去,到达对边后,再返回,这样往复数次.图中的实线和虚线分别表示甲、乙与游泳池固定一边的距离随游泳时间变化的情况,根据图形回答:
(1)甲、乙两人分别游了几个来回?
(2)甲游了多长时间?游泳的速度是多少?
(3)在整个游泳过程中,甲、乙两人相遇了几次?
15.2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平.自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销,下面表示2020年初至脱销期间,该厂库存量y(吨)与时间t(天)之间关系的大致图象是( )
参考答案:
1.在三角形ABC中,它的底边是a,底边上的高是h,则三角形面积S=ah,当a为定长时,在此式子中(A)
A.S,h是变量,,a是常量
B.S,h,a是变量,是常量
C.a,h是变量,,S是常量
D.S是变量,,a,h是常量
2.小亮帮母亲预算家庭4月份电费开支情况,下表是小亮家4月初连续8天每天早上电表显示的读数:
日期/日
1
2
3
4
5
6
7
8
电表读数/度
21
24
28
33
39
42
46
49
表格中反映的变量是日期和电表读数,自变量是日期,因变量是电表读数.
3.日常生活中,我们经常要烧开水,下表是对烧水的时间与水的温度的记录:
时间
(分)
1
2
3
4
5
6
7
8
9
10
11
12
13
温度
(℃)
25
29
32
43
52
61
72
81
90
98
100
100
100
(1)上表反映了哪些变量之间的关系?
(2)根据表格的数据判断:在第15分钟时,水的温度为多少?
(3)随着加热时间的增加,水的温度是否会一直上升?
解:(1)烧水的时间与水的温度.
(2)100 ℃.
(3)随着加热时间的增加,在1到11分钟时,水的温度一直上升,在11分钟后温度保持不变,都为100 ℃.
4.如图,一轮船从离A港10千米的P地出发向B港匀速行驶,30分钟后离A港26千米(未到达B港).设x小时后,轮船离A港y千米(未到达B港),则y与x之间的关系式为y=10+32x.
5.球的体积V与半径R之间的关系式是V=πR3.
(1)在这个式子中,常量、变量分别是什么?
(2)利用这个式子分别求出当球的半径为2 cm,3 cm,4 cm时球的体积;
(3)若R>1,当球的半径增大时,球的体积如何变化?
解:(1)在这个式子中,常量是π,变量是球的体积V和半径R.
(2)当球的半径为2 cm时,球的体积是
π×23=π(cm3);
当球的半径为3 cm时,球的体积是
π×33=36π(cm3);
当球的半径为4 cm时,球的体积是
π×43=π(cm3).
(3)若R>1,当球的半径增大时,球的体积也增大.
6.“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用x表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是(A)
A B
C D
7.如图所示是某港口某天从8 h到20 h的水深情况,根据图象回答下列问题:
(1)在8 h到20 h这段时间内,大约什么时间港口的水位最深,深度是多少米?
(2)大约什么时候港口的水位最浅,是多少?
(3)在这段时间里,水深是如何变化的?
解:(1)13 h,7.5 m.
(2)8 h,2 m.
(3)8 h~13 h,水位不断上升;
13 h~15 h,水位不断下降;
15 h~20 h,水位又开始上升.
8.小颖画了一个边长为5 cm的正方形,如果将正方形的边长增加x(cm),那么面积的增加值y(cm2)与边长的增加值x(cm)之间的关系式为y=x2+10x.
9.(2020·青海)将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度h(cm)与注水时间t(min)的图象大致为图中的(B)
10.小明从家出发步行至学校,停留一段时间后乘车返回,则下列图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是(B)
11.一空水池现需注满水,水池深4.9 m,现以不变的流量注水,数据如下表.其中不变的量是流量,可以推断注满水池所需的时间是3.5_h.
水的深度h/m
0.7
1.4
2.1
2.8
注水时间t/h
0.5
1
1.5
2
12.如图反映了某出租公司乘车费用y(元)与路程x(千米)之间的关系,请你根据图中信息回答下列问题:
(1)公司规定的起步价是10元;
(2)该公司规定除起步价外,超过5千米的每增加1千米多收1.7元;
(3)若你是一名乘客,共付了44元钱,则你的行程是25千米.
13.如图1,在直角梯形ABCD中,动点P从点B出发,沿B→C→D→A匀速运动,设点P运动的路程为x,三角形ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是x、y;
(2)当点P运动的路程x=4时,三角形ABP的面积y=16;
(3)求AB的长和梯形ABCD的面积.
解:根据图象,得BC=4,三角形ABC的面积为16,
所以AB·BC=16,
即×AB×4=16,解得AB=8.
由图象,得DC=9-4=5,
则S梯形ABCD=BC·(DC+AB)=×4×(5+8)=26.
14.一游泳池长90 m,甲、乙两人分别从两对边同时向所对的另一边游去,到达对边后,再返回,这样往复数次.图中的实线和虚线分别表示甲、乙与游泳池固定一边的距离随游泳时间变化的情况,根据图形回答:
(1)甲、乙两人分别游了几个来回?
(2)甲游了多长时间?游泳的速度是多少?
(3)在整个游泳过程中,甲、乙两人相遇了几次?
解:(1)甲游了三个来回,乙游了两个来回.
(2)甲游了180 s,速度为3 m/s.
(3)在整个游泳过程中,甲、乙两人相遇了5次.
15.2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平.自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销,下面表示2020年初至脱销期间,该厂库存量y(吨)与时间t(天)之间关系的大致图象是(D)
1.在三角形ABC中,它的底边是a,底边上的高是h,则三角形面积S=ah,当a为定长时,在此式子中( )
A.S,h是变量,,a是常量
B.S,h,a是变量,是常量
C.a,h是变量,,S是常量
D.S是变量,,a,h是常量
2.小亮帮母亲预算家庭4月份电费开支情况,下表是小亮家4月初连续8天每天早上电表显示的读数:
日期/日
1
2
3
4
5
6
7
8
电表读数/度
21
24
28
33
39
42
46
49
表格中反映的变量是 ,自变量是 ,因变量是 .
3.日常生活中,我们经常要烧开水,下表是对烧水的时间与水的温度的记录:
时间
(分)
1
2
3
4
5
6
7
8
9
10
11
12
13
温度
(℃)
25
29
32
43
52
61
72
81
90
98
100
100
100
(1)上表反映了哪些变量之间的关系?
(2)根据表格的数据判断:在第15分钟时,水的温度为多少?
(3)随着加热时间的增加,水的温度是否会一直上升?
4.如图,一轮船从离A港10千米的P地出发向B港匀速行驶,30分钟后离A港26千米(未到达B港).设x小时后,轮船离A港y千米(未到达B港),则y与x之间的关系式为 .
5.球的体积V与半径R之间的关系式是V=πR3.
(1)在这个式子中,常量、变量分别是什么?
(2)利用这个式子分别求出当球的半径为2 cm,3 cm,4 cm时球的体积;
(3)若R>1,当球的半径增大时,球的体积如何变化?
6.“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用x表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是( )
A B
C D
7.如图所示是某港口某天从8 h到20 h的水深情况,根据图象回答下列问题:
(1)在8 h到20 h这段时间内,大约什么时间港口的水位最深,深度是多少米?
(2)大约什么时候港口的水位最浅,是多少?
(3)在这段时间里,水深是如何变化的?
8.小颖画了一个边长为5 cm的正方形,如果将正方形的边长增加x(cm),那么面积的增加值y(cm2)与边长的增加值x(cm)之间的关系式为 .
9.将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度h(cm)与注水时间t(min)的图象大致为图中的( )
10.小明从家出发步行至学校,停留一段时间后乘车返回,则下列图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )
11.一空水池现需注满水,水池深4.9 m,现以不变的流量注水,数据如下表.其中不变的量是 ,可以推断注满水池所需的时间是 .
水的深度h/m
0.7
1.4
2.1
2.8
注水时间t/h
0.5
1
1.5
2
12.如图反映了某出租公司乘车费用y(元)与路程x(千米)之间的关系,请你根据图中信息回答下列问题:
(1)公司规定的起步价是 元;
(2)该公司规定除起步价外,超过5千米的每增加1千米多收 元;
(3)若你是一名乘客,共付了44元钱,则你的行程是 千米.
13.如图1,在直角梯形ABCD中,动点P从点B出发,沿B→C→D→A匀速运动,设点P运动的路程为x,三角形ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 、 ;
(2)当点P运动的路程x=4时,三角形ABP的面积y= ;
(3)求AB的长和梯形ABCD的面积.
14.一游泳池长90 m,甲、乙两人分别从两对边同时向所对的另一边游去,到达对边后,再返回,这样往复数次.图中的实线和虚线分别表示甲、乙与游泳池固定一边的距离随游泳时间变化的情况,根据图形回答:
(1)甲、乙两人分别游了几个来回?
(2)甲游了多长时间?游泳的速度是多少?
(3)在整个游泳过程中,甲、乙两人相遇了几次?
15.2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平.自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销,下面表示2020年初至脱销期间,该厂库存量y(吨)与时间t(天)之间关系的大致图象是( )
参考答案:
1.在三角形ABC中,它的底边是a,底边上的高是h,则三角形面积S=ah,当a为定长时,在此式子中(A)
A.S,h是变量,,a是常量
B.S,h,a是变量,是常量
C.a,h是变量,,S是常量
D.S是变量,,a,h是常量
2.小亮帮母亲预算家庭4月份电费开支情况,下表是小亮家4月初连续8天每天早上电表显示的读数:
日期/日
1
2
3
4
5
6
7
8
电表读数/度
21
24
28
33
39
42
46
49
表格中反映的变量是日期和电表读数,自变量是日期,因变量是电表读数.
3.日常生活中,我们经常要烧开水,下表是对烧水的时间与水的温度的记录:
时间
(分)
1
2
3
4
5
6
7
8
9
10
11
12
13
温度
(℃)
25
29
32
43
52
61
72
81
90
98
100
100
100
(1)上表反映了哪些变量之间的关系?
(2)根据表格的数据判断:在第15分钟时,水的温度为多少?
(3)随着加热时间的增加,水的温度是否会一直上升?
解:(1)烧水的时间与水的温度.
(2)100 ℃.
(3)随着加热时间的增加,在1到11分钟时,水的温度一直上升,在11分钟后温度保持不变,都为100 ℃.
4.如图,一轮船从离A港10千米的P地出发向B港匀速行驶,30分钟后离A港26千米(未到达B港).设x小时后,轮船离A港y千米(未到达B港),则y与x之间的关系式为y=10+32x.
5.球的体积V与半径R之间的关系式是V=πR3.
(1)在这个式子中,常量、变量分别是什么?
(2)利用这个式子分别求出当球的半径为2 cm,3 cm,4 cm时球的体积;
(3)若R>1,当球的半径增大时,球的体积如何变化?
解:(1)在这个式子中,常量是π,变量是球的体积V和半径R.
(2)当球的半径为2 cm时,球的体积是
π×23=π(cm3);
当球的半径为3 cm时,球的体积是
π×33=36π(cm3);
当球的半径为4 cm时,球的体积是
π×43=π(cm3).
(3)若R>1,当球的半径增大时,球的体积也增大.
6.“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用x表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是(A)
A B
C D
7.如图所示是某港口某天从8 h到20 h的水深情况,根据图象回答下列问题:
(1)在8 h到20 h这段时间内,大约什么时间港口的水位最深,深度是多少米?
(2)大约什么时候港口的水位最浅,是多少?
(3)在这段时间里,水深是如何变化的?
解:(1)13 h,7.5 m.
(2)8 h,2 m.
(3)8 h~13 h,水位不断上升;
13 h~15 h,水位不断下降;
15 h~20 h,水位又开始上升.
8.小颖画了一个边长为5 cm的正方形,如果将正方形的边长增加x(cm),那么面积的增加值y(cm2)与边长的增加值x(cm)之间的关系式为y=x2+10x.
9.(2020·青海)将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度h(cm)与注水时间t(min)的图象大致为图中的(B)
10.小明从家出发步行至学校,停留一段时间后乘车返回,则下列图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是(B)
11.一空水池现需注满水,水池深4.9 m,现以不变的流量注水,数据如下表.其中不变的量是流量,可以推断注满水池所需的时间是3.5_h.
水的深度h/m
0.7
1.4
2.1
2.8
注水时间t/h
0.5
1
1.5
2
12.如图反映了某出租公司乘车费用y(元)与路程x(千米)之间的关系,请你根据图中信息回答下列问题:
(1)公司规定的起步价是10元;
(2)该公司规定除起步价外,超过5千米的每增加1千米多收1.7元;
(3)若你是一名乘客,共付了44元钱,则你的行程是25千米.
13.如图1,在直角梯形ABCD中,动点P从点B出发,沿B→C→D→A匀速运动,设点P运动的路程为x,三角形ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是x、y;
(2)当点P运动的路程x=4时,三角形ABP的面积y=16;
(3)求AB的长和梯形ABCD的面积.
解:根据图象,得BC=4,三角形ABC的面积为16,
所以AB·BC=16,
即×AB×4=16,解得AB=8.
由图象,得DC=9-4=5,
则S梯形ABCD=BC·(DC+AB)=×4×(5+8)=26.
14.一游泳池长90 m,甲、乙两人分别从两对边同时向所对的另一边游去,到达对边后,再返回,这样往复数次.图中的实线和虚线分别表示甲、乙与游泳池固定一边的距离随游泳时间变化的情况,根据图形回答:
(1)甲、乙两人分别游了几个来回?
(2)甲游了多长时间?游泳的速度是多少?
(3)在整个游泳过程中,甲、乙两人相遇了几次?
解:(1)甲游了三个来回,乙游了两个来回.
(2)甲游了180 s,速度为3 m/s.
(3)在整个游泳过程中,甲、乙两人相遇了5次.
15.2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平.自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销,下面表示2020年初至脱销期间,该厂库存量y(吨)与时间t(天)之间关系的大致图象是(D)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
