第10讲 反比例函数与几何综合题-2021年中考数学二轮复习重点题型针对训练(北师大版)(含答案)
文档属性
| 名称 | 第10讲 反比例函数与几何综合题-2021年中考数学二轮复习重点题型针对训练(北师大版)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 562.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 17:52:58 | ||
图片预览



文档简介
《重点题型专项复习》第10讲 反比例函数与几何综合题
【思路方法】
一.总体解题思路
二.具体思路方法
1.走“点的坐标”→→求或设点的坐标;辅助线:作x或y轴垂线;
2.走“k值与几何基础面积图形”→→构造出基础图形,寻找题目条件图形与基础图形间的转化关系;
【强化巩固练习】
1. 如图,反比例函数y1=k1x与一次函数y2=k2x+b的交点横坐标为1,4,则不等式k1x A. x≤4 B. x<0或1≤x≤4 C. x<0或x≥4 D. x≤1或x≥4
2. 函数false和falsefalse在同一直角坐标系中的大致图象是( )
A. B. C. D.
3.已知反比例函数y=abx的图象如图所示,则二次函数y=ax2?2x和一次函数y=bx+a在同一平面直角坐标系中的图象可能是( )
4.反比例函数y=kx与一次函数y=-kx+1在同一坐标系的图像可能是( )
5.二次函数y=ax2+bx+c的图像如右图所示,反比例函数y=abx与正比例函数y=(2a+c)x在同一坐标系内的大致图像是( )
6.下列选项中不正确的是( )
A.反比例函数y=kx(k≠0)的图象只有1条对称轴
B.若ab<0,则抛物线y=ax2﹣2x+b与x轴有两个交点
C.将二次函数y=﹣3(x﹣1)2的图象向左平移1个单位得到y=﹣3x2的图象
D.若反比例函数y=﹣3x三图象过点(a,﹣2),(b,﹣3),则a>b
7. 如图,已知某人对地面的压强 P 与他和地面接触面积 S 的函数关系如图所示,若经过一稀泥地地面能承
受的压强不超过 500N/m,那么要想不至于下陷,必须站立的木板面积(木板的重量忽略不计)是( )
A. 大于85 B. 小于85 C. 至少85 D. 至多85
8.如图,过反比例函数y=2x(x>0)上一点A作y轴的平行线交反比例函数y=kx(x>0)于点B,连接OA,OB,若S?AOB=3,则k的值为( )
A. 3 B. -3 C. 4 D. -4
9.如图,菱形OABC的边OC在x轴上,且周长为10,已知cos∠COA=35,若反比例函数y=kx(k>0)经过点A,则k=_______
10.如图,已知直线y=12x+1交x轴于点A,交反比例函数y=kx(x>0)于点B,过点B作BC⊥AB交反比例函数于点C,若BC=12AB,则k的值为_____________
11.如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,OA=5,tan∠COA=34.若反比例函数y=kx
(k>0,x>0)经过点C,则k的值等于________.
52387556515
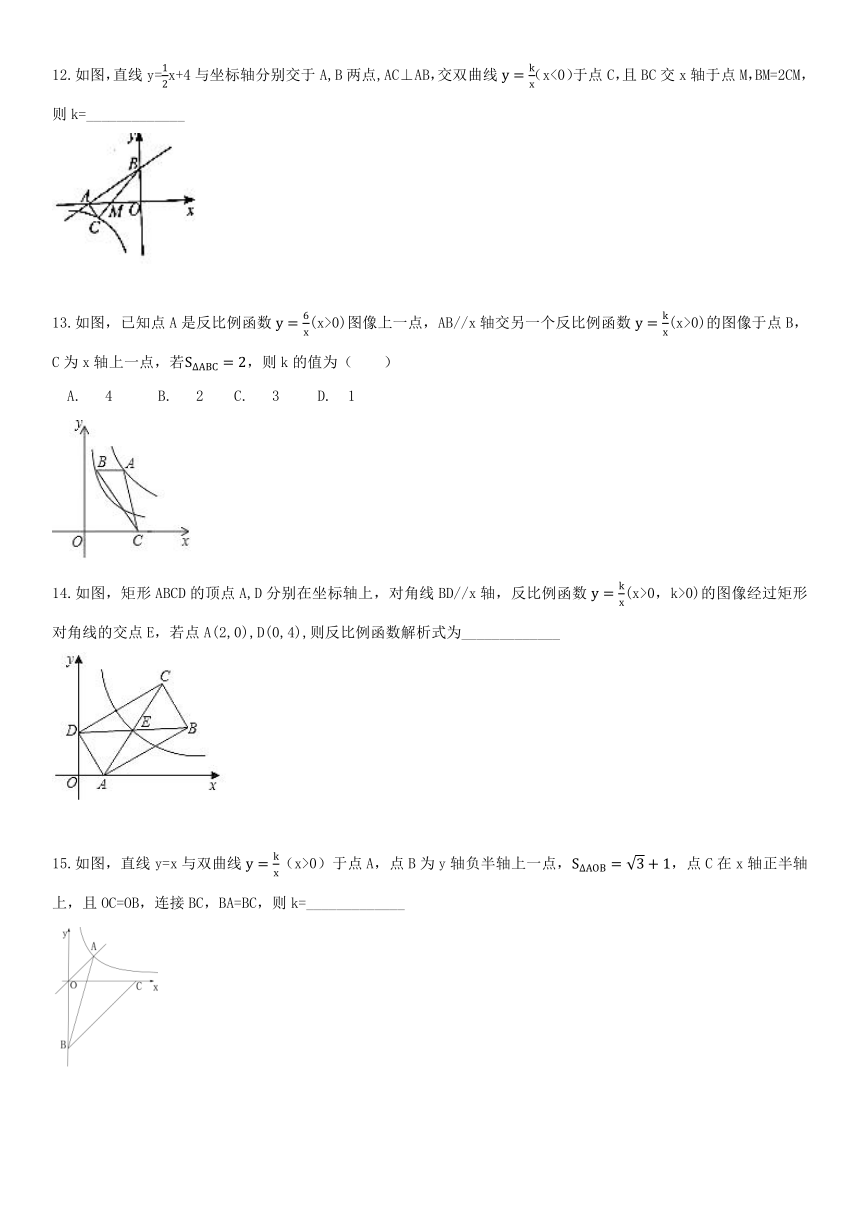
12.如图,直线y=12x+4与坐标轴分别交于A,B两点,AC⊥AB,交双曲线y=kx(x<0)于点C,且BC交x轴于点M,BM=2CM,则k=_____________
13.如图,已知点A是反比例函数y=6x(x>0)图像上一点,AB//x轴交另一个反比例函数y=kx(x>0)的图像于点B,C为x轴上一点,若S?ABC=2,则k的值为( )
A. 4 B. 2 C. 3 D. 1
14.如图,矩形ABCD的顶点A,D分别在坐标轴上,对角线BD//x轴,反比例函数y=kx(x>0,k>0)的图像经过矩形对角线的交点E,若点A(2,0),D(0,4),则反比例函数解析式为_____________
15.如图,直线y=x与双曲线y=kx(x>0)于点A,点B为y轴负半轴上一点,S?AOB=3+1,点C在x轴正半轴上,且OC=OB,连接BC,BA=BC,则k=_____________
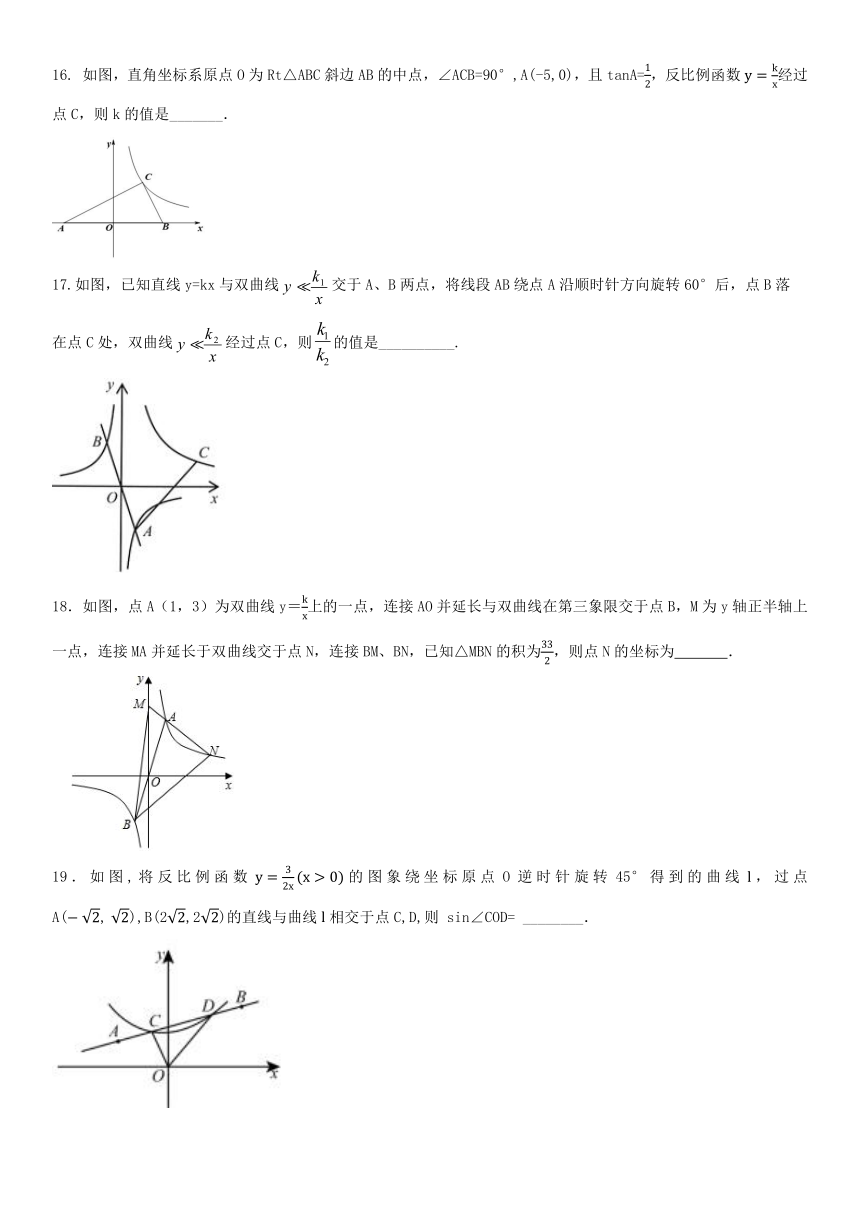
16. 如图,直角坐标系原点O为Rt△ABC斜边AB的中点,∠ACB=90°,A(-5,0),且tanA=12,反比例函数y=kx经过点C,则k的值是_______.
17.如图,已知直线y=kx与双曲线false交于A、B两点,将线段AB绕点A沿顺时针方向旋转60°后,点B落
在点C处,双曲线false经过点C,则false的值是__________.
18.如图,点A(1,3)为双曲线y=kx上的一点,连接AO并延长与双曲线在第三象限交于点B,M为y轴正半轴上
一点,连接MA并延长于双曲线交于点N,连接BM、BN,已知△MBN的积为332,则点N的坐标为 .
19.如图,将反比例函数y=32x(x>0)的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点 A(?2, 2),B(22,22)的直线与曲线l相交于点C,D,则 sin∠COD= ________.
20.点A(﹣3,1),B(﹣2,2),反比例函数y=kx(k<0,x<0)的图象记为L.
(1)若L经过点A.
①图象L的解析式为 .
②点B在图象L上,还是在图象L的上方或下方?为什么?
(2)如图在(1)的条件下,L上纵坐标为3的点P与点C关于原点O对称,PQ⊥x轴于点Q,CD⊥x轴于点D.求△QCD的面积.
(3)若L与线段AB有公共点,直接写出k的取值范围.
21. 如图,直线AD:y=3x+3与坐标轴交于A,D两点,以AD为边在AD右侧作正方形ABCD,过C作CG⊥y轴于G点.过点C的反比例函数y=kx与直线AD交于E,F两点.
(1)求证:△AOD≌△DGC;
(2)求E、F两点坐标;
(3)填空:不等式3x+3>kx的取值范围是_________.
22.如图1,一次函数y=kx-3的图像与y轴交于点B,与反比例函数y=mx(x>0)交于A(8,1)
(1)k=_______;m=__________;
(2)点C是线段AB上一点(不与A,B重合),过点C作y轴的平行线与该反比例函数的图像交于点D,连接OC,OD,AD,当四边形OCAD的面积等于24时,求点C的坐标;
(3)在(2)的前提下,将△OCD沿射线BA方向平移一定的距离后,得到△O`C`D`,若点O对应点O`恰好落在该反比例函数图像上,如图2,请直接写出此时点D的对应点D`的坐标;
23.如图,直线y=3x+b经过点A(-1,0),与y轴正半轴交于点B,与反比例函数y=kx(x>0)交于点C,且BC=2AB,BD//x轴交反比例函数于点D,连接AD.
(1)b=_____,k=______;
(2)求△ABD的面积;
(3)若E为射线BC上一点,设E的横坐标为m,过点E作EF//BD,交反比例函数的图像于点F,且EF=13BD.,求m的值。
【答案详解】
1. 如图,反比例函数y1=k1x与一次函数y2=k2x+b的交点横坐标为1,4,则不等式k1x A. x≤4 B. x<0或1≤x≤4 C. x<0或x≥4 D. x≤1或x≥4
【解析】
不等式k1x2. 函数false和falsefalse在同一直角坐标系中的大致图象是( )
A. B. C. D.
【解析】
在函数false和false中,当false时,函数false的图象在第一、三象限,
函数false的图象在第一、二、三象限,
故选项A、D错误,选项B正确,
当false时,函数false的图象在第二、四象限,
函数false的图象在第一、二、四象限,
故选项C错误,
故选B.
3.已知反比例函数y=abx的图象如图所示,则二次函数y=ax2?2x和一次函数y=bx+a在同一平面直角坐标系中的图象可能是( )
【解析】
由反比例函数图像可知ab>0,
则当a,b均为正数时,二次函数开口向上,
一次函数经过一、二、三象限,
故选C
4.反比例函数y=kx与一次函数y=-kx+1在同一坐标系的图像可能是( )
【解析】
若k>0,则反比例函数经过一、三象限,
则-k<0,
则一次函数经过一、二、四象限,
故选B
5.二次函数y=ax2+bx+c的图像如右图所示,反比例函数y=abx与正比例函数y=(2a+c)x在同一坐标系内的大致图像是( )
【解析】
由抛物线图像可得:a<0,b>0,c>0,
则ab<0,由对称轴可得b=-a,
当x=-1时a-b+c<0,
则2a+c<0,
故选B
6.下列选项中不正确的是( )
A.反比例函数y=kx(k≠0)的图象只有1条对称轴
B.若ab<0,则抛物线y=ax2﹣2x+b与x轴有两个交点
C.将二次函数y=﹣3(x﹣1)2的图象向左平移1个单位得到y=﹣3x2的图象
D.若反比例函数y=﹣3x三图象过点(a,﹣2),(b,﹣3),则a>b
【解析】
反比例函数图像有2条对称轴,分别是一、三;二、四象限的角平分线,
故选A
7. 如图,已知某人对地面的压强 P 与他和地面接触面积 S 的函数关系如图所示,若经过一稀泥地地面能承
受的压强不超过 500N/m,那么要想不至于下陷,必须站立的木板面积(木板的重量忽略不计)是( )
A. 大于85 B. 小于85 C. 至少85 D. 至多85
【解析】由图可知P=800S,当P≤500时,S≥85,故选C
8.如图,过反比例函数y=2x(x>0)上一点A作y轴的平行线交反比例函数y=kx(x>0)于点B,连接OA,OB,若S?AOB=3,则k的值为( )
A. 3 B. -3 C. 4 D. -4
【解析】由图可知S?AOB=22+?k2=3,解得k=-4,故选D
9.如图,菱形OABC的边OC在x轴上,且周长为10,已知cos∠COA=35,若反比例函数y=kx(k>0)经过点A,则k=_______
【解析】
作AD⊥OC于点D,由周长可得OA=2.5,
由cos∠COA=35可得OD=1.5,
则AD=2,
则k=2S?AOD=3
10.如图,已知直线y=12x+1交x轴于点A,交反比例函数y=kx(x>0)于点B,过点B作BC⊥AB交反比例函数于点C,若BC=12AB,则k的值为_____________
【解析】
由题可知A(-2,0),OA=2,
如图构造“一线三垂直模型”,
则BDAE=CDBE=BCAB=12,
设B(a, 12a+1),
∴OE=a,BE=12a+1,AE=a+2,CD=14a+12,BD=12a+1,
∴C(34a?12,a+2),
∵B,C均在反比例函数图像上,
∴a( 12a+1)=(34a?12)(a+2),
解得a=2,
则k= a( 12a+1)=4
11.如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,OA=5,tan∠COA=34.若反比例函数y=kx
(k>0,x>0)经过点C,则k的值等于________.
52387556515
【解析】
有三角函数,必构造Rt△,
故作CD⊥x轴于点D,
由OC=OA=5, tan∠COA=34
易得OD=4,CD=3,
则C(4,3),则k=12
40386075565
12.如图,直线y=12x+4与坐标轴分别交于A,B两点,AC⊥AB,交双曲线y=kx(x<0)于点C,且BC交x轴于点M,BM=2CM,则k=_____________
【解析】
由题可得:A(-8,0),B(0,4),
作CE⊥x轴于点E,
由BM=2CM及OBCE=BMCM
可得CE=2,
由AC⊥AB可设直线AC的解析式为y=-2x+b,
代入A点坐标可得y=-2x-4,
当y=-2时x=-1,
∴C(-1,-2),
则k=2
13.如图,已知点A是反比例函数y=6x(x>0)图像上一点,AB//x轴交另一个反比例函数y=kx(x>0)的图像于点B,C为x轴上一点,若S?ABC=2,则k的值为( )
A. 4 B. 2 C. 3 D. 1
【解析】
延长AB交y轴于点D,
由AB//x轴可得S?ABC=S?AB0=2,
由反比例函数y=6x可得S?AD0=3,
∴S?DB0=1,
∴k=2,
故选B
14.如图,矩形ABCD的顶点A,D分别在坐标轴上,对角线BD//x轴,反比例函数y=kx(x>0,k>0)的图像经过矩形对角线的交点E,若点A(2,0),D(0,4),则反比例函数解析式为_____________
【解析】
由BD//x轴可设B(x,4),
由AD2+AB2=BD2可列方程为22+42+(x?2)2+42=x2,
解得x=10,
则B(10,4),
由中点坐标公式可得E(5,4),
∴k=5×4=20,
∴反比例函数解析式为y=20x
15.如图,直线y=x与双曲线y=kx(x>0)于点A,点B为y轴负半轴上一点,S?AOB=3+1,点C在x轴正半轴上,且OC=OB,连接BC,BA=BC,则k=_____________
【解析】
设A(m,m),
则AD=OD=m,
由S?AOB=3+1可得OB=23+2m,
则BD=23+2m+m,
BC=2×23+2m = 26+22m,
由BA=BC可得BA2=BC2,
则AD2+BD2=BC2,
即(23+2m+m)2+m2=( 26+22m)2,
化简为m4+2+23m2?(8+43)=0,
十字相乘分解可得:m2?2m2+4+23=0,
解得m2=2或m2=?4?23(舍去),
∴k=m2=2
16. 如图,直角坐标系原点O为Rt△ABC斜边AB的中点,∠ACB=90°,A(-5,0),且tanA=12,反比例函数y=kx经过点C,则k的值是_______.
【解析】作CD⊥AB于点D.由tanA=12可设BC=x,AC=2x,根据勾股定理即可求出BC和AC的值,利用面积法求出CD的值,再利用勾股定理求出BD的值,得到点C的坐标,然后可求出k的值.
【详解】如图,作CD⊥AB于点D.
∵A(-5,0),O为Rt△ABC斜边AB的中点,
∴B(5,0),
∴OB=5,AB=10.
∵tanA=12=BCAC,
∴可设BC=x,AC=2x,
由勾股定理得x2+(2x)2=102,
∴x=25,
∴BC=25,AC=45,
∵12AC?BC=12AB?CD,
∴25×45=10CD,
∴CD=4,
∴BD=BC2?CD2=(25)2?42=2,
∴OD=5-2=3,
∴C(3,4).反比例函数y=kx经过点C,
∴k=3×4=12.
17.如图,已知直线y=kx与双曲线false交于A、B两点,将线段AB绕点A沿顺时针方向旋转60°后,点B落
在点C处,双曲线false经过点C,则false的值是__________.
【解析】
连接 BC、OC,过点 B 作 BD⊥x 轴于 D,过点 C 作 CE⊥x轴于点E,
易得△OBD∽△COE,且相似比是1:3,
即面积比为1:3,
∵k1<0,k2>0,
∴false=-13
18.如图,点A(1,3)为双曲线y=kx上的一点,连接AO并延长与双曲线在第三象限交于点B,M为y轴正半轴上
一点,连接MA并延长于双曲线交于点N,连接BM、BN,已知△MBN的积为332,则点N的坐标为 .
【解析】反比例函数与正比例函数同时出现的反比例函数几何综合题,一定要紧抓住“O是A,B的中点”解题,
连接ON,则S?AON=S?BON,S?AOM=S?BOM,
∴S?MON=12S?MBN=334,
由A点坐标可得反比例函数解析式为y=3x,
设M(0,m),
则由S?MON=334
可得12m?xN=334,
可得xN=332m,
∵N在反比例函数图像上,则N点坐标为(332m,2m11),
由M,A两点坐标可得可得直线MA的解析式为y=(3-m)x+m,
将N点坐标代入y=(3-m)x+m,
可得33(3?m)2m+m=2m11,
解得m=113或332,332m=92或1(与A点重合故舍去),
∴N点坐标为(92,23)
19.如图,将反比例函数y=32x(x>0)的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点 A(?2, 2),B(22,22)的直线与曲线l相交于点C,D,则 sin∠COD= ________.
【解析】
依旋转性质可知,将图形绕点O顺时针旋转45°后∠COD的大小不会发生变化,
则点A的对应点A`(0,2),点B的对应点B`(4,0),
则直线A`B`的解析式为y=?12x+2,
联立方程y=?12x+2y=32x ,
解得C`(1, 32),D`(3, 12),
如图构造“一线三垂直模型”,
易得直线OC`的解析式为y=32x,
设P点坐标为(a,32a),PN=3-a,ND`=32a?12,
则由△OMD`∽△D`NP
可得OMND`=D`MNP,
即332a?12=123?a,
解得a=3715,
∴P(3715,3710),
由两点间距离公式可得PD`=83715,OP=371330,
∴sin∠COD=83715371330=16481481
20.点A(﹣3,1),B(﹣2,2),反比例函数y=kx(k<0,x<0)的图象记为L.
(1)若L经过点A.
①图象L的解析式为 .
②点B在图象L上,还是在图象L的上方或下方?为什么?
(2)如图在(1)的条件下,L上纵坐标为3的点P与点C关于原点O对称,PQ⊥x轴于点Q,CD⊥x轴于点D.求△QCD的面积.
(3)若L与线段AB有公共点,直接写出k的取值范围.
【解析】
(1)①∵L经过点A,
∴k=-3×1=-3,
∴图象L的解析式为y=?3x(x<0)
②点B在图像L的上方,理由是:
当x=-2时,y=?3?2=32≠2,
∴L不经过点B,
∵32<2,
∴点B在L的上方.
(2)由点P的纵坐标为3,
则当y=3,x=-1,
∴P(-1,3),
∴S?POQ=12|k|=32,
∵点Q与点C关于原点对称,且PQ⊥x轴,CD⊥x轴,
∴DQ=2OQ,CD=PQ,
∴S?QCD=2S?POQ=3.
(3)当L过点A时,k=-3,
当L过点B时,k=-4,
∴若L与线段AB有公共点时k的取值范围-4≤x≤-3.
21. 如图,直线AD:y=3x+3与坐标轴交于A,D两点,以AD为边在AD右侧作正方形ABCD,过C作CG⊥y轴于G点.过点C的反比例函数y=kx与直线AD交于E,F两点.
(1)求证:△AOD≌△DGC;
(2)求E、F两点坐标;
(3)填空:不等式3x+3>kx的取值范围是_________.
【解析】
(1)由题意易得AD=CD,∠ADC=90°,进而可得∠ADO=∠DCG,然后问题可求证;
(2)由直线AD的解析式可求出A(-1,0),D(0,3),由(1)可得DG=OA=1,CG=OD=3,则有OG=2,然后联立一次函数与反比例函数解析可求解;
(3)由(2)及图像可直接进行求解.
(1)证明:∵正方形ABCD,
∴AD=CD,∠ADC=90°,
∵∠AOD=∠DGC=90°,
∴∠ADO+∠GDC=∠DCG+∠GDC=90°
∴∠ADO=∠DCG,
∴△AOD≌△DGC;
(2)解:∵y=3x+3=0时,x=-1,
∴A(-1,0),D(0,3),
由(1)可知DG=OA=1,CG=OD=3,
∴OG=2,
即C(3,2),
即y=6x,
联立y=3x+3y=6x ,
解得:x1=?2,x2=1;
∴E(1,6),F(-2,-3);
(3)由图像及(2)可得:
不等式3x+3>kx的取值范围是-21;
22.如图1,一次函数y=kx-3的图像与y轴交于点B,与反比例函数y=mx(x>0)交于A(8,1)
(1)k=_______;m=__________;
(2)点C是线段AB上一点(不与A,B重合),过点C作y轴的平行线与该反比例函数的图像交于点D,连接OC,OD,AD,当四边形OCAD的面积等于24时,求点C的坐标;
(3)在(2)的前提下,将△OCD沿射线BA方向平移一定的距离后,得到△O`C`D`,若点O对应点O`恰好落在该反比例函数图像上,如图2,请直接写出此时点D的对应点D`的坐标;
【解析】
(1)k=,12,m=8;
(2)∵点C是线段AB上一点,
∴C点坐标为(a, 12a-3),
则D(a, 8a)
∴CD=8a? 12a+3,
当四边形OCAD的面积等于24时,
∴SOCAD=S?OCD+S?ACD=128a? 12a+3?a+128a? 12a+3?(8?a)=24,
整理得a2?6a?16=0,
解得a=2或-8(舍去),
∴C(2,-2)
(3)由平移性质可得OO`//AB,
则直线OO`的解析式为y=12x,
联立方程y=12xy=8x,
解得x=4或-4(舍去),
则O`坐标为(4,2),
则△OCD向右平移4个单位,再向上平移2个单位,得到△O`C`D`,
由(2)可知D(2,4),
∴D`(6,6)
23.如图,直线y=3x+b经过点A(-1,0),与y轴正半轴交于点B,与反比例函数y=kx(x>0)交于点C,且BC=2AB,BD//x轴交反比例函数于点D,连接AD.
(1)b=_____,k=______;
(2)求△ABD的面积;
(3)若E为射线BC上一点,设E的横坐标为m,过点E作EF//BD,交反比例函数的图像于点F,且EF=13BD.,求m的值。
【解析】
(1)将A点坐标代入y=3x+b中,可得b=3,
∴B(0,3),OB=3,
作CG⊥y轴于点G,
由CG//OA
可得OACG=OBBG=ABBC=12,
可得CG=2,BG=6,
∴OG=9,
∴C(2,9),
∴k=2×9=18;
(2)由BD//x轴可得D点纵坐标为3,
由D点横坐标为18÷3=6,
∴D(6,3),BD=6,
∴S?ABD=12×6×3=9
(3)由EF=13BD.,BD=6,
可得EF=2,
设E(m,3m+3),
①当F点在E点右侧时,
由EF//BD可得F(m+2, 3m+3),
∵F点在反比例函数图像上,
∴(m+2)( 3m+3)=18,
解得m=1或m=-4(舍去);
②当F点在E点左侧时,
由EF//BD可得F(m-2, 3m+3),
∵F点在反比例函数图像上,
∴(m-2)( 3m+3)=18,
解得m=1+332或m=1?332 (舍去);
综上所述,m=1或1+332
【思路方法】
一.总体解题思路
二.具体思路方法
1.走“点的坐标”→→求或设点的坐标;辅助线:作x或y轴垂线;
2.走“k值与几何基础面积图形”→→构造出基础图形,寻找题目条件图形与基础图形间的转化关系;
【强化巩固练习】
1. 如图,反比例函数y1=k1x与一次函数y2=k2x+b的交点横坐标为1,4,则不等式k1x
2. 函数false和falsefalse在同一直角坐标系中的大致图象是( )
A. B. C. D.
3.已知反比例函数y=abx的图象如图所示,则二次函数y=ax2?2x和一次函数y=bx+a在同一平面直角坐标系中的图象可能是( )
4.反比例函数y=kx与一次函数y=-kx+1在同一坐标系的图像可能是( )
5.二次函数y=ax2+bx+c的图像如右图所示,反比例函数y=abx与正比例函数y=(2a+c)x在同一坐标系内的大致图像是( )
6.下列选项中不正确的是( )
A.反比例函数y=kx(k≠0)的图象只有1条对称轴
B.若ab<0,则抛物线y=ax2﹣2x+b与x轴有两个交点
C.将二次函数y=﹣3(x﹣1)2的图象向左平移1个单位得到y=﹣3x2的图象
D.若反比例函数y=﹣3x三图象过点(a,﹣2),(b,﹣3),则a>b
7. 如图,已知某人对地面的压强 P 与他和地面接触面积 S 的函数关系如图所示,若经过一稀泥地地面能承
受的压强不超过 500N/m,那么要想不至于下陷,必须站立的木板面积(木板的重量忽略不计)是( )
A. 大于85 B. 小于85 C. 至少85 D. 至多85
8.如图,过反比例函数y=2x(x>0)上一点A作y轴的平行线交反比例函数y=kx(x>0)于点B,连接OA,OB,若S?AOB=3,则k的值为( )
A. 3 B. -3 C. 4 D. -4
9.如图,菱形OABC的边OC在x轴上,且周长为10,已知cos∠COA=35,若反比例函数y=kx(k>0)经过点A,则k=_______
10.如图,已知直线y=12x+1交x轴于点A,交反比例函数y=kx(x>0)于点B,过点B作BC⊥AB交反比例函数于点C,若BC=12AB,则k的值为_____________
11.如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,OA=5,tan∠COA=34.若反比例函数y=kx
(k>0,x>0)经过点C,则k的值等于________.
52387556515
12.如图,直线y=12x+4与坐标轴分别交于A,B两点,AC⊥AB,交双曲线y=kx(x<0)于点C,且BC交x轴于点M,BM=2CM,则k=_____________
13.如图,已知点A是反比例函数y=6x(x>0)图像上一点,AB//x轴交另一个反比例函数y=kx(x>0)的图像于点B,C为x轴上一点,若S?ABC=2,则k的值为( )
A. 4 B. 2 C. 3 D. 1
14.如图,矩形ABCD的顶点A,D分别在坐标轴上,对角线BD//x轴,反比例函数y=kx(x>0,k>0)的图像经过矩形对角线的交点E,若点A(2,0),D(0,4),则反比例函数解析式为_____________
15.如图,直线y=x与双曲线y=kx(x>0)于点A,点B为y轴负半轴上一点,S?AOB=3+1,点C在x轴正半轴上,且OC=OB,连接BC,BA=BC,则k=_____________
16. 如图,直角坐标系原点O为Rt△ABC斜边AB的中点,∠ACB=90°,A(-5,0),且tanA=12,反比例函数y=kx经过点C,则k的值是_______.
17.如图,已知直线y=kx与双曲线false交于A、B两点,将线段AB绕点A沿顺时针方向旋转60°后,点B落
在点C处,双曲线false经过点C,则false的值是__________.
18.如图,点A(1,3)为双曲线y=kx上的一点,连接AO并延长与双曲线在第三象限交于点B,M为y轴正半轴上
一点,连接MA并延长于双曲线交于点N,连接BM、BN,已知△MBN的积为332,则点N的坐标为 .
19.如图,将反比例函数y=32x(x>0)的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点 A(?2, 2),B(22,22)的直线与曲线l相交于点C,D,则 sin∠COD= ________.
20.点A(﹣3,1),B(﹣2,2),反比例函数y=kx(k<0,x<0)的图象记为L.
(1)若L经过点A.
①图象L的解析式为 .
②点B在图象L上,还是在图象L的上方或下方?为什么?
(2)如图在(1)的条件下,L上纵坐标为3的点P与点C关于原点O对称,PQ⊥x轴于点Q,CD⊥x轴于点D.求△QCD的面积.
(3)若L与线段AB有公共点,直接写出k的取值范围.
21. 如图,直线AD:y=3x+3与坐标轴交于A,D两点,以AD为边在AD右侧作正方形ABCD,过C作CG⊥y轴于G点.过点C的反比例函数y=kx与直线AD交于E,F两点.
(1)求证:△AOD≌△DGC;
(2)求E、F两点坐标;
(3)填空:不等式3x+3>kx的取值范围是_________.
22.如图1,一次函数y=kx-3的图像与y轴交于点B,与反比例函数y=mx(x>0)交于A(8,1)
(1)k=_______;m=__________;
(2)点C是线段AB上一点(不与A,B重合),过点C作y轴的平行线与该反比例函数的图像交于点D,连接OC,OD,AD,当四边形OCAD的面积等于24时,求点C的坐标;
(3)在(2)的前提下,将△OCD沿射线BA方向平移一定的距离后,得到△O`C`D`,若点O对应点O`恰好落在该反比例函数图像上,如图2,请直接写出此时点D的对应点D`的坐标;
23.如图,直线y=3x+b经过点A(-1,0),与y轴正半轴交于点B,与反比例函数y=kx(x>0)交于点C,且BC=2AB,BD//x轴交反比例函数于点D,连接AD.
(1)b=_____,k=______;
(2)求△ABD的面积;
(3)若E为射线BC上一点,设E的横坐标为m,过点E作EF//BD,交反比例函数的图像于点F,且EF=13BD.,求m的值。
【答案详解】
1. 如图,反比例函数y1=k1x与一次函数y2=k2x+b的交点横坐标为1,4,则不等式k1x
【解析】
不等式k1x
A. B. C. D.
【解析】
在函数false和false中,当false时,函数false的图象在第一、三象限,
函数false的图象在第一、二、三象限,
故选项A、D错误,选项B正确,
当false时,函数false的图象在第二、四象限,
函数false的图象在第一、二、四象限,
故选项C错误,
故选B.
3.已知反比例函数y=abx的图象如图所示,则二次函数y=ax2?2x和一次函数y=bx+a在同一平面直角坐标系中的图象可能是( )
【解析】
由反比例函数图像可知ab>0,
则当a,b均为正数时,二次函数开口向上,
一次函数经过一、二、三象限,
故选C
4.反比例函数y=kx与一次函数y=-kx+1在同一坐标系的图像可能是( )
【解析】
若k>0,则反比例函数经过一、三象限,
则-k<0,
则一次函数经过一、二、四象限,
故选B
5.二次函数y=ax2+bx+c的图像如右图所示,反比例函数y=abx与正比例函数y=(2a+c)x在同一坐标系内的大致图像是( )
【解析】
由抛物线图像可得:a<0,b>0,c>0,
则ab<0,由对称轴可得b=-a,
当x=-1时a-b+c<0,
则2a+c<0,
故选B
6.下列选项中不正确的是( )
A.反比例函数y=kx(k≠0)的图象只有1条对称轴
B.若ab<0,则抛物线y=ax2﹣2x+b与x轴有两个交点
C.将二次函数y=﹣3(x﹣1)2的图象向左平移1个单位得到y=﹣3x2的图象
D.若反比例函数y=﹣3x三图象过点(a,﹣2),(b,﹣3),则a>b
【解析】
反比例函数图像有2条对称轴,分别是一、三;二、四象限的角平分线,
故选A
7. 如图,已知某人对地面的压强 P 与他和地面接触面积 S 的函数关系如图所示,若经过一稀泥地地面能承
受的压强不超过 500N/m,那么要想不至于下陷,必须站立的木板面积(木板的重量忽略不计)是( )
A. 大于85 B. 小于85 C. 至少85 D. 至多85
【解析】由图可知P=800S,当P≤500时,S≥85,故选C
8.如图,过反比例函数y=2x(x>0)上一点A作y轴的平行线交反比例函数y=kx(x>0)于点B,连接OA,OB,若S?AOB=3,则k的值为( )
A. 3 B. -3 C. 4 D. -4
【解析】由图可知S?AOB=22+?k2=3,解得k=-4,故选D
9.如图,菱形OABC的边OC在x轴上,且周长为10,已知cos∠COA=35,若反比例函数y=kx(k>0)经过点A,则k=_______
【解析】
作AD⊥OC于点D,由周长可得OA=2.5,
由cos∠COA=35可得OD=1.5,
则AD=2,
则k=2S?AOD=3
10.如图,已知直线y=12x+1交x轴于点A,交反比例函数y=kx(x>0)于点B,过点B作BC⊥AB交反比例函数于点C,若BC=12AB,则k的值为_____________
【解析】
由题可知A(-2,0),OA=2,
如图构造“一线三垂直模型”,
则BDAE=CDBE=BCAB=12,
设B(a, 12a+1),
∴OE=a,BE=12a+1,AE=a+2,CD=14a+12,BD=12a+1,
∴C(34a?12,a+2),
∵B,C均在反比例函数图像上,
∴a( 12a+1)=(34a?12)(a+2),
解得a=2,
则k= a( 12a+1)=4
11.如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,OA=5,tan∠COA=34.若反比例函数y=kx
(k>0,x>0)经过点C,则k的值等于________.
52387556515
【解析】
有三角函数,必构造Rt△,
故作CD⊥x轴于点D,
由OC=OA=5, tan∠COA=34
易得OD=4,CD=3,
则C(4,3),则k=12
40386075565
12.如图,直线y=12x+4与坐标轴分别交于A,B两点,AC⊥AB,交双曲线y=kx(x<0)于点C,且BC交x轴于点M,BM=2CM,则k=_____________
【解析】
由题可得:A(-8,0),B(0,4),
作CE⊥x轴于点E,
由BM=2CM及OBCE=BMCM
可得CE=2,
由AC⊥AB可设直线AC的解析式为y=-2x+b,
代入A点坐标可得y=-2x-4,
当y=-2时x=-1,
∴C(-1,-2),
则k=2
13.如图,已知点A是反比例函数y=6x(x>0)图像上一点,AB//x轴交另一个反比例函数y=kx(x>0)的图像于点B,C为x轴上一点,若S?ABC=2,则k的值为( )
A. 4 B. 2 C. 3 D. 1
【解析】
延长AB交y轴于点D,
由AB//x轴可得S?ABC=S?AB0=2,
由反比例函数y=6x可得S?AD0=3,
∴S?DB0=1,
∴k=2,
故选B
14.如图,矩形ABCD的顶点A,D分别在坐标轴上,对角线BD//x轴,反比例函数y=kx(x>0,k>0)的图像经过矩形对角线的交点E,若点A(2,0),D(0,4),则反比例函数解析式为_____________
【解析】
由BD//x轴可设B(x,4),
由AD2+AB2=BD2可列方程为22+42+(x?2)2+42=x2,
解得x=10,
则B(10,4),
由中点坐标公式可得E(5,4),
∴k=5×4=20,
∴反比例函数解析式为y=20x
15.如图,直线y=x与双曲线y=kx(x>0)于点A,点B为y轴负半轴上一点,S?AOB=3+1,点C在x轴正半轴上,且OC=OB,连接BC,BA=BC,则k=_____________
【解析】
设A(m,m),
则AD=OD=m,
由S?AOB=3+1可得OB=23+2m,
则BD=23+2m+m,
BC=2×23+2m = 26+22m,
由BA=BC可得BA2=BC2,
则AD2+BD2=BC2,
即(23+2m+m)2+m2=( 26+22m)2,
化简为m4+2+23m2?(8+43)=0,
十字相乘分解可得:m2?2m2+4+23=0,
解得m2=2或m2=?4?23(舍去),
∴k=m2=2
16. 如图,直角坐标系原点O为Rt△ABC斜边AB的中点,∠ACB=90°,A(-5,0),且tanA=12,反比例函数y=kx经过点C,则k的值是_______.
【解析】作CD⊥AB于点D.由tanA=12可设BC=x,AC=2x,根据勾股定理即可求出BC和AC的值,利用面积法求出CD的值,再利用勾股定理求出BD的值,得到点C的坐标,然后可求出k的值.
【详解】如图,作CD⊥AB于点D.
∵A(-5,0),O为Rt△ABC斜边AB的中点,
∴B(5,0),
∴OB=5,AB=10.
∵tanA=12=BCAC,
∴可设BC=x,AC=2x,
由勾股定理得x2+(2x)2=102,
∴x=25,
∴BC=25,AC=45,
∵12AC?BC=12AB?CD,
∴25×45=10CD,
∴CD=4,
∴BD=BC2?CD2=(25)2?42=2,
∴OD=5-2=3,
∴C(3,4).反比例函数y=kx经过点C,
∴k=3×4=12.
17.如图,已知直线y=kx与双曲线false交于A、B两点,将线段AB绕点A沿顺时针方向旋转60°后,点B落
在点C处,双曲线false经过点C,则false的值是__________.
【解析】
连接 BC、OC,过点 B 作 BD⊥x 轴于 D,过点 C 作 CE⊥x轴于点E,
易得△OBD∽△COE,且相似比是1:3,
即面积比为1:3,
∵k1<0,k2>0,
∴false=-13
18.如图,点A(1,3)为双曲线y=kx上的一点,连接AO并延长与双曲线在第三象限交于点B,M为y轴正半轴上
一点,连接MA并延长于双曲线交于点N,连接BM、BN,已知△MBN的积为332,则点N的坐标为 .
【解析】反比例函数与正比例函数同时出现的反比例函数几何综合题,一定要紧抓住“O是A,B的中点”解题,
连接ON,则S?AON=S?BON,S?AOM=S?BOM,
∴S?MON=12S?MBN=334,
由A点坐标可得反比例函数解析式为y=3x,
设M(0,m),
则由S?MON=334
可得12m?xN=334,
可得xN=332m,
∵N在反比例函数图像上,则N点坐标为(332m,2m11),
由M,A两点坐标可得可得直线MA的解析式为y=(3-m)x+m,
将N点坐标代入y=(3-m)x+m,
可得33(3?m)2m+m=2m11,
解得m=113或332,332m=92或1(与A点重合故舍去),
∴N点坐标为(92,23)
19.如图,将反比例函数y=32x(x>0)的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点 A(?2, 2),B(22,22)的直线与曲线l相交于点C,D,则 sin∠COD= ________.
【解析】
依旋转性质可知,将图形绕点O顺时针旋转45°后∠COD的大小不会发生变化,
则点A的对应点A`(0,2),点B的对应点B`(4,0),
则直线A`B`的解析式为y=?12x+2,
联立方程y=?12x+2y=32x ,
解得C`(1, 32),D`(3, 12),
如图构造“一线三垂直模型”,
易得直线OC`的解析式为y=32x,
设P点坐标为(a,32a),PN=3-a,ND`=32a?12,
则由△OMD`∽△D`NP
可得OMND`=D`MNP,
即332a?12=123?a,
解得a=3715,
∴P(3715,3710),
由两点间距离公式可得PD`=83715,OP=371330,
∴sin∠COD=83715371330=16481481
20.点A(﹣3,1),B(﹣2,2),反比例函数y=kx(k<0,x<0)的图象记为L.
(1)若L经过点A.
①图象L的解析式为 .
②点B在图象L上,还是在图象L的上方或下方?为什么?
(2)如图在(1)的条件下,L上纵坐标为3的点P与点C关于原点O对称,PQ⊥x轴于点Q,CD⊥x轴于点D.求△QCD的面积.
(3)若L与线段AB有公共点,直接写出k的取值范围.
【解析】
(1)①∵L经过点A,
∴k=-3×1=-3,
∴图象L的解析式为y=?3x(x<0)
②点B在图像L的上方,理由是:
当x=-2时,y=?3?2=32≠2,
∴L不经过点B,
∵32<2,
∴点B在L的上方.
(2)由点P的纵坐标为3,
则当y=3,x=-1,
∴P(-1,3),
∴S?POQ=12|k|=32,
∵点Q与点C关于原点对称,且PQ⊥x轴,CD⊥x轴,
∴DQ=2OQ,CD=PQ,
∴S?QCD=2S?POQ=3.
(3)当L过点A时,k=-3,
当L过点B时,k=-4,
∴若L与线段AB有公共点时k的取值范围-4≤x≤-3.
21. 如图,直线AD:y=3x+3与坐标轴交于A,D两点,以AD为边在AD右侧作正方形ABCD,过C作CG⊥y轴于G点.过点C的反比例函数y=kx与直线AD交于E,F两点.
(1)求证:△AOD≌△DGC;
(2)求E、F两点坐标;
(3)填空:不等式3x+3>kx的取值范围是_________.
【解析】
(1)由题意易得AD=CD,∠ADC=90°,进而可得∠ADO=∠DCG,然后问题可求证;
(2)由直线AD的解析式可求出A(-1,0),D(0,3),由(1)可得DG=OA=1,CG=OD=3,则有OG=2,然后联立一次函数与反比例函数解析可求解;
(3)由(2)及图像可直接进行求解.
(1)证明:∵正方形ABCD,
∴AD=CD,∠ADC=90°,
∵∠AOD=∠DGC=90°,
∴∠ADO+∠GDC=∠DCG+∠GDC=90°
∴∠ADO=∠DCG,
∴△AOD≌△DGC;
(2)解:∵y=3x+3=0时,x=-1,
∴A(-1,0),D(0,3),
由(1)可知DG=OA=1,CG=OD=3,
∴OG=2,
即C(3,2),
即y=6x,
联立y=3x+3y=6x ,
解得:x1=?2,x2=1;
∴E(1,6),F(-2,-3);
(3)由图像及(2)可得:
不等式3x+3>kx的取值范围是-2
22.如图1,一次函数y=kx-3的图像与y轴交于点B,与反比例函数y=mx(x>0)交于A(8,1)
(1)k=_______;m=__________;
(2)点C是线段AB上一点(不与A,B重合),过点C作y轴的平行线与该反比例函数的图像交于点D,连接OC,OD,AD,当四边形OCAD的面积等于24时,求点C的坐标;
(3)在(2)的前提下,将△OCD沿射线BA方向平移一定的距离后,得到△O`C`D`,若点O对应点O`恰好落在该反比例函数图像上,如图2,请直接写出此时点D的对应点D`的坐标;
【解析】
(1)k=,12,m=8;
(2)∵点C是线段AB上一点,
∴C点坐标为(a, 12a-3),
则D(a, 8a)
∴CD=8a? 12a+3,
当四边形OCAD的面积等于24时,
∴SOCAD=S?OCD+S?ACD=128a? 12a+3?a+128a? 12a+3?(8?a)=24,
整理得a2?6a?16=0,
解得a=2或-8(舍去),
∴C(2,-2)
(3)由平移性质可得OO`//AB,
则直线OO`的解析式为y=12x,
联立方程y=12xy=8x,
解得x=4或-4(舍去),
则O`坐标为(4,2),
则△OCD向右平移4个单位,再向上平移2个单位,得到△O`C`D`,
由(2)可知D(2,4),
∴D`(6,6)
23.如图,直线y=3x+b经过点A(-1,0),与y轴正半轴交于点B,与反比例函数y=kx(x>0)交于点C,且BC=2AB,BD//x轴交反比例函数于点D,连接AD.
(1)b=_____,k=______;
(2)求△ABD的面积;
(3)若E为射线BC上一点,设E的横坐标为m,过点E作EF//BD,交反比例函数的图像于点F,且EF=13BD.,求m的值。
【解析】
(1)将A点坐标代入y=3x+b中,可得b=3,
∴B(0,3),OB=3,
作CG⊥y轴于点G,
由CG//OA
可得OACG=OBBG=ABBC=12,
可得CG=2,BG=6,
∴OG=9,
∴C(2,9),
∴k=2×9=18;
(2)由BD//x轴可得D点纵坐标为3,
由D点横坐标为18÷3=6,
∴D(6,3),BD=6,
∴S?ABD=12×6×3=9
(3)由EF=13BD.,BD=6,
可得EF=2,
设E(m,3m+3),
①当F点在E点右侧时,
由EF//BD可得F(m+2, 3m+3),
∵F点在反比例函数图像上,
∴(m+2)( 3m+3)=18,
解得m=1或m=-4(舍去);
②当F点在E点左侧时,
由EF//BD可得F(m-2, 3m+3),
∵F点在反比例函数图像上,
∴(m-2)( 3m+3)=18,
解得m=1+332或m=1?332 (舍去);
综上所述,m=1或1+332
同课章节目录
