第13讲 二次函数几何综合压轴题-2021年中考数学二轮复习重点题型针对训练(北师大版)(含答案)
文档属性
| 名称 | 第13讲 二次函数几何综合压轴题-2021年中考数学二轮复习重点题型针对训练(北师大版)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 577.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 17:55:38 | ||
图片预览



文档简介
《重点题型专项复习》第13讲 二次函数几何综合压轴题
【思路方法】
1.总体解题思路
left-635
2.总体解题方法
(1)代数论证方法
(2)几何论证方法
3.具体思考角度
【点】
①交点→→联立方程解答;
②图像上的点→→代入法或依解析式设点的坐标;
③中点→→中点坐标公式;
【直线】
①正常情况→→“待定系数法”
②平行线→→K值相等;
③垂直线→→K值负倒数;
【线段】
①点的坐标表示水平或垂直线段→→一定遵循“右减左、上减下”原则,不明确时加上绝对值;
②利用两点间的距离公式表示或计算线段长度;
③利用有关几何性质表示或计算线段长度;
④距离或高→→点到直线的距离公式:
如P(m,n)到直线y=kx+b的距离或高,先把直线的函数表达式变形为方程形式:kx-y+b=0,代入公式
公式:d=|km?n+b|1+k2
⑤线段比或线段积→利用相似三角形性质转化
【角】
①三角函数→→Rt△→→“一线三垂直模型”
②等角性质→→如等边对等角、平行、全等或相似性质等
③和差倍分角→→首先转化成某角的具体度数或一对等角;
【三角形】
①等腰三角形→→一定要结合“边(腰)相等”、“底边三线合一”这两性质展开分析思考;
②直角三角形→→一定要利用好直角走 “一线三垂直模型”、“垂直k值负倒数”、 “勾股定理”等思路;
③三角形相似→→一定要抓住相似性质“对应边成比例”、“对应角相似”、“面积比等于相似比平方”等思路;
【特殊四边形】
①平行四边形
代数→→对角线平行+中点坐标公式;
几何:→→作垂线,走全等;
②菱形
代数→→对角线平行+中点坐标公式+邻边相等;
几何:→→对角线垂直,走Rt△+邻边相等;
③矩形
代数→→对角线平行+中点坐标公式+邻边垂直;
几何:→→对角线相等,走Rt△;
【最值】
①单一线段最值
代数→→字母表示,走二次函数配方;
几何:→→①三个特殊位置法,走点到直线距离;②转化成将军饮马问题;
②线段和差(周长)最值
代数→→字母表示,走二次函数配方;
几何:→→①三个特殊位置法,走点到直线距离;②转化成将军饮马问题;
③面积最值
代数→→字母表示,走二次函数配方;
几何:→→转化成高或底的线段最值问题;
④定值
代数→→字母表示,约分成具体数值;
几何:→→利用相似等几何性质,转化成与已知线段相联系;
【面积方法】→→“铅垂法”、“割补法”、“公式法”、“相似的面积比或不相似时平行线间的底之比”
【强化巩固练习】
1.在平面直角坐标系中,抛物线y=ax2+bx+c经过点A、B、C,已知A(-1,0),B(6,0),C(0,-6).
(1)求此抛物线的函数表达式;
(2)若点D为第四象限内抛物线上一动点,当△BCD面积最大时,求△BCD面积最大值;
(3)在x轴上是否存在点M,使∠OCM+∠ACO=45°,若存在,请求出点M的坐标;若不存在,请说明理由.
2.如图1,抛物线y=14x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴负半轴交于点C,OC=OB=10.
(1)求抛物线解析式;
(2)点P,Q在第四象限内抛物线上,点P在点Q下方,连接CP,CQ,∠OCP+∠OCQ=180°,设点Q的横坐标为m,点P的横坐标为n,求m与n的函数关系式;
(3)如图2,在(2)的条件下,连接AP交CO于点D,过点Q作QE⊥AB于点E,连接BQ,DE,是否存在点P,使∠AED=2∠EQB,若存在,求出点P的坐标;若不存在,请说明理由。
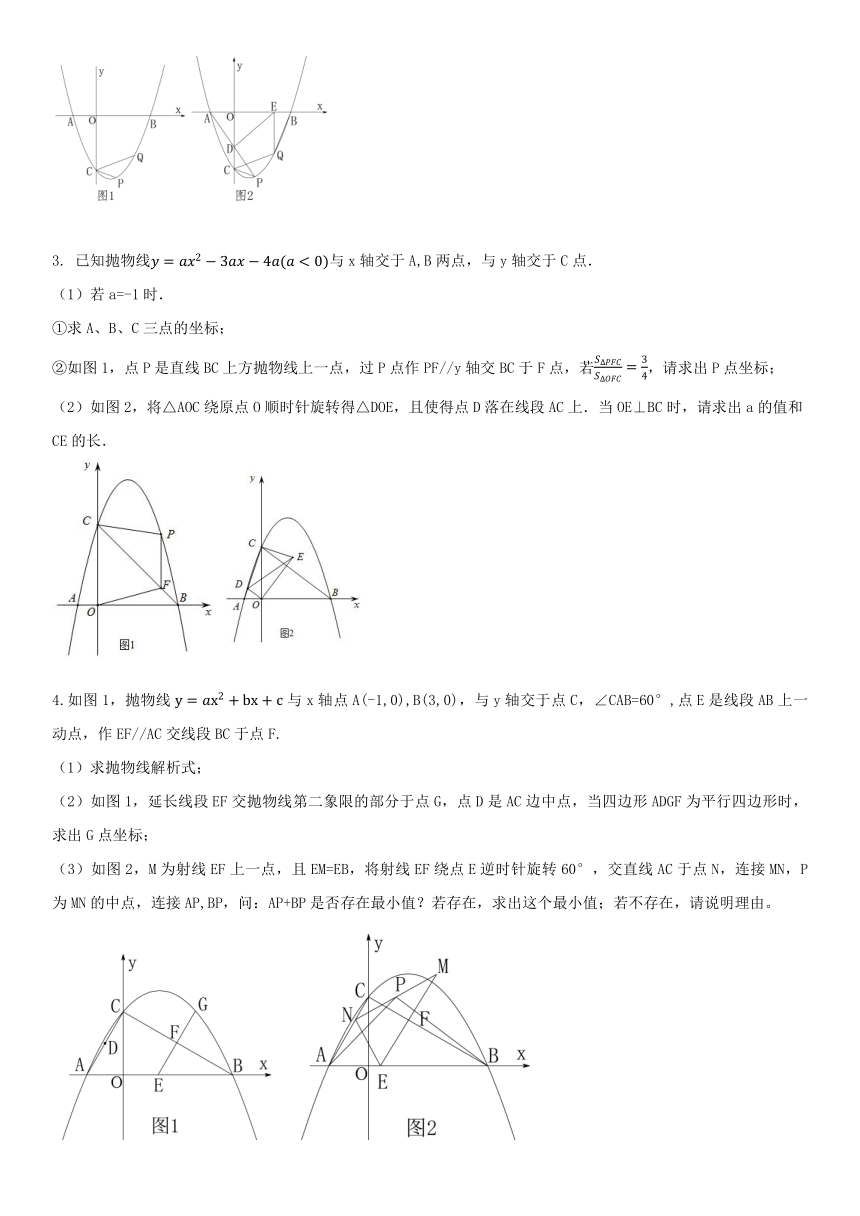
3. 已知抛物线y=ax2?3ax?4a(a<0)与x轴交于A,B两点,与y轴交于C点.
(1)若a=-1时.
①求A、B、C三点的坐标;
②如图1,点P是直线BC上方抛物线上一点,过P点作PF//y轴交BC于F点,若S?PFCS?OFC=34,请求出P点坐标;
(2)如图2,将△AOC绕原点O顺时针旋转得△DOE,且使得点D落在线段AC上.当OE⊥BC时,请求出a的值和CE的长.
4.如图1,抛物线y=ax2+bx+c与x轴点A(-1,0),B(3,0),与y轴交于点C,∠CAB=60°,点E是线段AB上一动点,作EF//AC交线段BC于点F.
(1)求抛物线解析式;
(2)如图1,延长线段EF交抛物线第二象限的部分于点G,点D是AC边中点,当四边形ADGF为平行四边形时,求出G点坐标;
(3)如图2,M为射线EF上一点,且EM=EB,将射线EF绕点E逆时针旋转60°,交直线AC于点N,连接MN,P为MN的中点,连接AP,BP,问:AP+BP是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由。
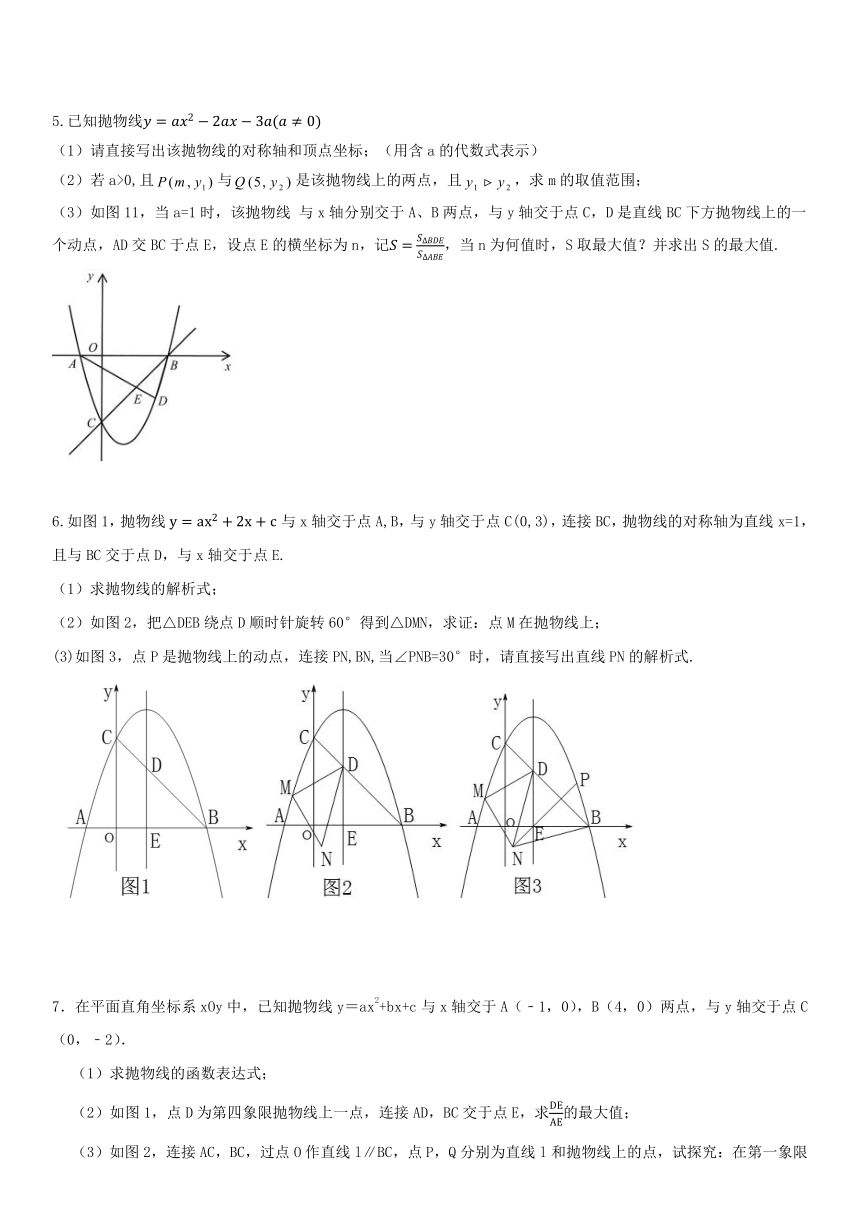
5.已知抛物线y=ax2?2ax?3a(a≠0)
请直接写出该抛物线的对称轴和顶点坐标;(用含a的代数式表示)
若a>0,且false与false是该抛物线上的两点,且false,求m的取值范围;
如图11,当a=1时,该抛物线 与x轴分别交于A、B两点,与y轴交于点C,D是直线BC下方抛物线上的一个动点,AD交BC于点E,设点E的横坐标为n,记S=S?BDES?ABE,当n为何值时,S取最大值?并求出S的最大值.
6.如图1,抛物线y=ax2+2x+c与x轴交于点A,B,与y轴交于点C(0,3),连接BC,抛物线的对称轴为直线x=1,且与BC交于点D,与x轴交于点E.
(1)求抛物线的解析式;
(2)如图2,把△DEB绕点D顺时针旋转60°得到△DMN,求证:点M在抛物线上;
(3)如图3,点P是抛物线上的动点,连接PN,BN,当∠PNB=30°时,请直接写出直线PN的解析式.
7.在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,﹣2).
(1)求抛物线的函数表达式;
(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,求DEAE的最大值;
(3)如图2,连接AC,BC,过点O作直线l∥BC,点P,Q分别为直线l和抛物线上的点,试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB.若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
8.如图1,直线yx2与x轴交于点B ,与y轴交于点C ,抛物线yax2 bx c(a 0)经过点A, B,C,点A的坐标为(1,0) .
(1)求二次函数yax2 bxc(a0)的表达式;
(2)抛物线的图像上是否存在点P,使得PCB 15 ,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图2,直线BC上有一动点D,连接AD,将线段AD绕点D顺时针旋转90 得到线段DE ,连接AE,BE.当AEBE取最小值时,若以A ,B ,E ,F为顶点的四边形是平行四边形,请直接写出E点和F点的坐标.
9.如图 1,抛物线y=mx2?3mx+n与x轴交于点( -1,0),与y轴交于点B(0,3 ) ,在线段OA上有一动点E (不与O 、A重合),过点E作x轴的垂线交直线AB于点N,交抛物线于点P.
(1)分别求出抛物线和直线 AB 的函数表达式;
(2)连接PA 、PB ,求△PAB面积的最大值,并求出此时点P的坐标;
(3)如图 2,点 E(2,0),将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E`A 、E`B,求E`A+23E`B的最小值
10.已知二次函数y=ax2+bx+c的图像与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C(0,-3).
(1)求二次函数的解析式;
(2)D是二次函数图像上位于第三象限内的点,求点D到直线AC的距离最大值时点D的坐标;
(3)M是二次函数图像对称轴上的点,在二次函数图像上是否存在点N,使以M、N、B、O为顶点的四边形是平行四边形?若有,请直接写出点N的坐标
11.如图1,已知抛物线y=-false(x+3)(x-4false)与x轴交于A、B两点,与false轴交于点C.
(1)(3分)写出A、B、C三点的坐标.
(2)(4分)若点P为△OBC内一点,求OP+BP+CP的最小值.
(3)(3分)如图2,点Q为对称轴左侧抛物线上一动点,点D(4,0),直线DQ分别与y轴、
直线AC交于E、F两点,当△CEF为等腰三角形时,请直接写出CE的长.
2324100142875504825133350
【答案详解】
1.在平面直角坐标系中,抛物线y=ax2+bx+c经过点A、B、C,已知A(-1,0),B(6,0),C(0,-6).
(1)求此抛物线的函数表达式;
(2)若点D为第四象限内抛物线上一动点,当△BCD面积最大时,求△BCD面积最大值;
(3)在x轴上是否存在点M,使∠OCM+∠ACO=45°,若存在,请求出点M的坐标;若不存在,请说明理由.
【解析】
(1)设交点式,代入点B坐标即可得抛物线解析式:y=x2?5x?6
(2) “铅垂法”+配方法解题。
如图1作DE//y轴交BC于点E,
设D(a, a2?5a?6),
由B,C可得直线BC的解析式为y=x-6,
则E(a,a-6),
则DE=a-6-(a2?5a?6)=? a2+6a,
则S?BCD=12OB?DE=12×6? a2+6a=?3a2+18a=? 3a?32++27,
当a=3时,S?BCD有最大值,最大值为27.
(3)二次函数典型题型:点角存在性问题。先把角的和差问题转化成一个角的问题,再按点角存在性问题的典型思路解题。
由B,C两点坐标可知,∠OCB=45?,
①当点M在y轴右侧时,∠OCM+∠ACO=45°,∠OCM+∠BCM=45?,
∴∠ACO=∠BCM,
则tan∠ACO=tan∠BCM=OAOC=16,
作BF⊥BC交CM于点F,过B作GP⊥x轴,作FG⊥GP于点G,作CP⊥GP于点P,
则由“一线三垂直模型”易得△FGB∽△BPC,
则FGBP=GBCP=FBBC=tan∠BCM=16,
∵CP=BP=6,
∴FG=GB=1,
∴F(5,1),
∴直线CF的表达式为y=75x?6,
∴M(307,0)
②作M关于点O的对称点M`,连接CM`,
则∠OCM=∠OCM`,
由∠OCM+∠ACO=45°
可得∠OCM`+∠ACO=45°,
点M`符合题目要求,
则M`(?307,0)
综上所述,点M的坐标为(307,0)或(-307,0)
2.如图1,抛物线y=14x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴负半轴交于点C,OC=OB=10.
(1)求抛物线解析式;
(2)点P,Q在第四象限内抛物线上,点P在点Q下方,连接CP,CQ,∠OCP+∠OCQ=180°,设点Q的横坐标为m,点P的横坐标为n,求m与n的函数关系式;
(3)如图2,在(2)的条件下,连接AP交CO于点D,过点Q作QE⊥AB于点E,连接BQ,DE,是否存在点P,使∠AED=2∠EQB,若存在,求出点P的坐标;若不存在,请说明理由。
【解析】
(1)由OC=OB=10可得C(0,-10),B(10,0),
代入可得抛物线解析式为:y=14x2?32x?10
(2)作QM⊥y轴交于点M,作PN⊥y轴交于点N,
设Q(m, 14m2?32m?10),P(n, 14n2?32n?10),
∵∠OCP+∠OCQ=180°,∠OCP+∠PCN=180°,
∴∠OCQ=∠PCN,
∴tan∠OCQ=tan∠PCN,
∴MQMC=NPCN,即 m14m2?32m= n?14n2+32n,
整理得:m=-n+12
(3)先把倍角转化为等角,再按点角性问题解题
作EH平分∠AED,则∠EQB=∠AEH,
则tan∠AEH=tan∠EQB=4m+4 ,
由角平分线性质联想到辅助线:作HA⊥x轴交EH于点H,作HM⊥ED交ED延长线于点M,
由对角平分线的对称性质可得AE=EM=m+4,HM=AH=4,
作HN⊥y轴于点N,
则ON=AH=4,HN=OA=4,
由HM=HN=4,DH=DH可证△HND≌△HMD,
可得MD=DN,作PF⊥x轴于点F,
则tan∠FAP=ODOA=PFAF=OD4=?14m2+32m+10n+4=n?10?4,
∴OD=10-n,
∵m=-n+12,
∴OD=m-2,
∴DM=DN=OD-ON=m-6,
∴DE=EM-DM=m+4-(m-6)=10,
在Rt△ODE中,由OE2+OD2=DE2可列方程为:
n2+(10?n)2=102,
即(12?n)2+(10?n)2=102,
解得n=4或18(舍去),
∴P(4,-12)
3. 已知抛物线y=ax2?3ax?4a(a<0)与x轴交于A,B两点,与y轴交于C点.
(1)若a=-1时.
①求A、B、C三点的坐标;
②如图1,点P是直线BC上方抛物线上一点,过P点作PF//y轴交BC于F点,若S?PFCS?OFC=34,请求出P点坐标;
(2)如图2,将△AOC绕原点O顺时针旋转得△DOE,且使得点D落在线段AC上.当OE⊥BC时,请求出a的值和CE的长.
【解析】
(1)①把a=-1代入解析式,分别令x=0和y=0即可求出A,B,C三点的坐标;
②先根据S?PFCS?OFC=34求出PF的值,再求出直线BC的解析式为,设P(m,?m2?3m+4),则F(m,-m+4),然后利用PF=3列方程求解即可;
(2)先证明AB=BC=5,再根据勾股定理求出OC的长,即可求出a的值;过O作OH⊥AD,根据cos∠OAC=AHAO=OAAC,可求出AH,然后利用△AOD∽△COE即可求出CE的值.
解:(1)若a=-1时
①原抛物线为y=?x2+3x+4,
当x=0时,y=4,
即C(0,4),
当y=0时,即?x2+3x+4=0时,
∴(x+1)(x-4)=0,
解得x1=?1,x2=4,
即A(-1,0),B(4,0);
②∵PF//y,
∴S?PFCS?OFC=PFOC=34,
∵OC=4,
∴PF=3,
设直线BC的解析式为:y=kx+b,
把B(4,0),C(0,4)代入,
得4k+b=0b=4 ,
∴b=4 k=?1,
∴y=-x+4,
设P(m,?m2?3m+4),
则F(m,-m+4),
∴PF=?m2?3m+4??m+4=?m2+4m=3,
解得m1=1,m2=3,
当m=1时,-m2+3m+4=-1+3+4=6;
当m=3时,-m2+3m+4=-9+9+4=4;
∴P1(1,6),P2(3,4);
(2)由旋转的性质得:OA=OD,∠DOE=∠AOC=90°,
∵OE⊥BC,
∴OD//BC,
∴∠DAO=∠ADO=∠ACB
,∴BA=BC=4+1=5,
∴OC=52?42=3,AC=12+32=10,
即OC=-4a=3,
∴a=-34.
过O作OH⊥AD,则cos∠OAC=AHAO=OAAC,
∴AH1=110,
∴AH=DH=1010,
∴AD=105.
由旋转的性质得,OA=OD,OC=OE,
∴OAOD=OCOE=1,
∵∠AOD+∠COD=90°,∠COE+∠COD=90°,
∴∠AOD=∠COE,
∴△AOD∽△COE,
∴ADCE=OAOC,
∵a=-34,
∴y=?34x2+94x+3,
当x=0时,y=3,
即C(0,3),
当y=0时,即?34x2+94x+3=0时,
∴(x+1)(x-4)=0,
解得x1=?1,x2=4,
即A(-1,0),B(4,0);
∴OA=1,OC=3,
∴ADCE=OAOC=13,
∴CE=3105.
4.如图1,抛物线y=ax2+bx+c与x轴点A(-1,0),B(3,0),与y轴交于点C,∠CAB=60°,点E是线段AB上一动点,作EF//AC交线段BC于点F.
(1)求抛物线解析式;
(2)如图1,延长线段EF交抛物线第二象限的部分于点G,点D是AC边中点,当四边形ADGF为平行四边形时,求出G点坐标;
(3)如图2,M为射线EF上一点,且EM=EB,将射线EF绕点E逆时针旋转60°,交直线AC于点N,连接MN,P为MN的中点,连接AP,BP,问:AP+BP是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由。
【解析】
(1)设抛物线交点式y=a(x+1)(x-3),
∵tan∠CAB=OCOA=tan60°,
∴OC=3,
∴C(0, 3),
把C点坐标代入解析式中,得a=?33,
∴抛物线解析式为y=?33x+1x?3=?33x2+233x+3;
(2)由题可得:AC2=4,BC2=12,AB2=16,
∵AC2+BC2=AB2,
∴∠ACB=90°, ∠ABC=30°,
由D是AC的中点可得AD=1,
当四边形ADGF为平行四边形时,AD=FG=1,AD//FG,
∴∠GFB=90°,
如图构造“一线三垂直模型”,则可得∠ABC=∠HFG=30°,
∴HG=12,FH=32 ,
设G(a, ?33a2+233a+3),
则F(a-12, ?33a2+233a+32),
由B,C两点坐标可得直线BC的解析为:y=?33x+3,
∵F在BC上,
∴?33a?12+3=?33a2+233a+32,
解得a=2或a=1,
∴G(1,433)或(2, 3)
(3)由题易证△ANE、△BEM均是等边三角形,
设E(m,0),则AE=m+1,BE=3-m,
则等边三角形性质“高=边长×32”
可得N(m?12, 3(m+1)2),M(3+m2, 3(3?m)2),
∵P是MN的中点,由中点坐标公式可得P(m+12, 3),
当E与A重合时N与A重合,
M在射线AC上,且AM=AB=4,
∵AC=2,故P0与C重合,
当E运动到AB中点时,AE=BE=2,
此时等边△ANE与等边△BEM全等,
这是点E的运动终点,
此时PE⊥x轴,P1 (1, 3),
点P就在线段P0P1间运动,
即P点在y轴与抛物线对称轴间的垂直于C点的线段y=3上运动,
作点A关于直线y=3的对称点A`(-1,23)false
连接A`B交直线y=3于点P,
此时,AP+BP=A`B=2 7.
5.已知抛物线y=ax2?2ax?3a(a≠0)
请直接写出该抛物线的对称轴和顶点坐标;(用含a的代数式表示)
若a>0,且false与false是该抛物线上的两点,且false,求m的取值范围;
如图11,当a=1时,该抛物线 与x轴分别交于A、B两点,与y轴交于点C,D是直线BC下方抛物线上的一个动点,AD交BC于点E,设点E的横坐标为n,记S=S?BDES?ABE,当n为何值时,S取最大值?并求出S的最大值.
【解析】
(1)对称轴是直线x=1;顶点坐标为(1,-4a).
(2)∵a>0,∴当x≥1时,y随x的增大而增大.
①当点P位于对称轴的右侧,即当m>1时,
∵y1>y2,
∴m>5;
②当点P位于对称轴的左侧,即当m<1时,
作点P关于对称轴的对称点Q,
则Q(2-m, y1),
∵y1>y2,
∴2-m>5,
解得m<-3;
∴m的取值范围是m<-3或m>5.
(3)当a=1时抛物线的解析式为y=x2?2x?3.
当y=0时x2?2x?3=0,
解得x1=3,x2=?1,
∴A(-1,0),B(3,0),
当x=0时y=-3,
∴C(0,-3),
∴直线BC的解析式为:y=x-3.
过点A作AF//y轴交直线BC于点F,作HD//y轴交直线BC于点G,交x轴于点D,
则△DEG∽△AEF,
∴S=S?BDES?ABE=DEAE=DGAF,
∵A(-1,0),
∴F(-1,4),
∴AF=4,
设D(a,a2?2a?3),
则G(a,a-3),
∴DG=a-3-(a2?2a?3)=?a2+3a,
∴S=?a2+3a4=?14(a?32)2+916,
∵?14<0,
∴当a=32时,S有最大值,且最大值为916,
此时点D的坐标为(32,?154).
∴直线AD的解析式为:y=-32x-32,
联立方程y=?32x?32y=x?3 ,
解得x=35y=?45,∴n=35.
∴当n=35时,S取最大值,最大值为916.
6.如图1,抛物线y=ax2+2x+c与x轴交于点A,B,与y轴交于点C(0,3),连接BC,抛物线的对称轴为直线x=1,且与BC交于点D,与x轴交于点E.
(1)求抛物线的解析式;
(2)如图2,把△DEB绕点D顺时针旋转60°得到△DMN,求证:点M在抛物线上;
(3)如图3,点P是抛物线上的动点,连接PN,BN,当∠PNB=30°时,请直接写出直线PN的解析式.
【解析】
(1)由对称轴x=1可知?b2a=?1a=1,
则a=-1,
由C点坐标可得c=3,
∴抛物线解析式为y=?x2+2x+3
(2)由抛物线解析式可知,
当y=0时?x2+2x+3=0
,解得x1=?1,x2=3,
∴A(-1,0),B(3,0),
由C(0,3),B(3,0)可得直线BC的解析式为y=-x+3,
则D(1,2),E(1,0),
则DE=2,
由旋转性质可得∠MDE=60°,MD=DE=2,
延长DM交x轴交于点G,作MH⊥x轴于点H,
则∠G=30°,
在Rt△GDE中由DE=2,
可得GD=4,DE=23,
则GM=2,
由MH//DE
可得GH:GE=MH:DE=GM:GD=2:4,
则可得MH=1,EH=3,
∴OH=3?1,
∴M(1-3,1),
当x=1-3时?x2+2x+3=?1?32+21?3+3=1,
∴点M在抛物线上;
(3)如图5,过点M作QR⊥x轴,作DQ⊥QR于Q,作NR⊥QR于点R,
由题可知△DEB为等腰直角三角形,
则△MDN是等腰直角三角形,
则△DQM≌△MRN,
则MR=DQ=3,RN=MQ=1,
∴N(2?3, 1?3),
由题可知DB=DN,∠BDN=60°,
∴△DNB是等边三角形,
①当P点在B点上方时,
∵∠PNB=30°,
由等边三角形“三线合一”性质可知NP垂直平分线段DB,
则题可知△EDB是等腰直角三角形,
∴E点在线段BD的垂直平分线NP上,
由N、E的坐标可得直线NP的解析式为y=x-1;
②当P点在B点下方时,
∵∠PNB=30°,∠DNB=60°,
∴∠DNP=90°,
由D、N两点坐标可得直线DN的解析式为:y=2+3x?3,
∴设直线NP的解析式为y=?2+3x+b,
代入N点坐标可得b=8-53,
∴直线NP的解析式为y=?2+3x+8?53,
综上所述,直线PN的解析式为y=x-1或y=?2+3x+8?53
7.在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,﹣2).
(1)求抛物线的函数表达式;
(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,求DEAE的最大值;
(3)如图2,连接AC,BC,过点O作直线l∥BC,点P,Q分别为直线l和抛物线上的点,试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB.若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
【解析】(1)设抛物线为交点式,
即y=a(x+1)(x-4),
代入C点坐标,
可得a=12,
∴抛物线解析式为y=12(x+1)(x-4)=12x2?32x?2
(2)构造相似典型图形“8字模型”,利用相似性质把DEAE用代数式表示出来,再利用二次函数配方法求最值。
作KA⊥x轴交直线BC于点K,作DG⊥x轴于点G,交直线BC于点F,
由B(4,0)、C(0,-2)可得直线BC的解析式为:y=12x-2,
则K(-1,-52),
则AK=52,
设D(a, 12a2?32a?2),
则F(a, 12a-2),则DF=12a-2-(12a2?32a?2)=?12a2+2a,
∵DF//AK,
∴DEAE=DFAK=?12a2+2a52=?15a2+45a=?15a?22+45,
即当a=2时,DEAE有最大值为45.
(3)由题可知:AC2=5,BC2=20,AB2=25,
∵AC2+BC2=AB2,
∴∠ACB=90°,
当△PQB∽△CAB时,
∠QPB=∠ACB=90°,BPQP=BCAC=205=2,
构造“一线三垂直模型”可求解点P的坐标;
又∵直线l∥BC,
∴直线l的表达式为y=12x.
①当P在Q点右侧时,如图,
过P作MN⊥x轴于N,作QM⊥MN于点M,
则△QMP∽△PNB,
∴BNMP=PNQM=BPQP=2
设P(2m,m),
则BN=2m-4,PN=m,
∴QM=12m,MP=m-2,
∴Q点坐标为(32m,2m-2),
将 Q点坐标代入抛物线解析式中得12×(32m)2?32×(32m)?2=2m?2,
解得m=349或m=0(舍去),
∴P点坐标为(689,349);
②当P在Q点左侧时,如图,
过P作MN⊥x轴于N,作QM⊥MN于点M,
则△QMP∽△PNB,
∴BNMP=PNQM=BPQP=2
设P(2m,m),
则BN=4-2m,PN=m,
∴QM=12m,MP=2-m,
∴Q点坐标为(52m,2),
将 Q点坐标代入抛物线解析式中得12×(52m)2?32×(52m)?2=2,
解得m=3+415或m=3?415 (舍去),
∴P点坐标为(6+2415,3+415);
综上所述,P的坐标为(689,349)或(6+2415,3+415)
8.如图1,直线yx2与x轴交于点B ,与y轴交于点C ,抛物线yax2 bx c(a 0)经过点A, B,C,点A的坐标为(1,0) .
(1)求二次函数yax2 bxc(a0)的表达式;
(2)抛物线的图像上是否存在点P,使得PCB 15 ,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图2,直线BC上有一动点D,连接AD,将线段AD绕点D顺时针旋转90 得到线段DE ,连接AE,BE.当AEBE取最小值时,若以A ,B ,E ,F为顶点的四边形是平行四边形,请直接写出E点和F点的坐标.
【解析】
(1)∵直线y=-x+2与x轴交于点B,与y轴交于点C,
∴B(2,0),C(0,2) .
∵抛物线交x轴于A,B两点,
∴设抛物线解析式为y=a(x+1)(x-2).
代入点C(0,2),
解得a=-1,
∴抛物线解析式为y=?x+1x?2=?x2+x+2.
(2)分以下两种情况:
①当点P在BC的下方时,
设CP交x轴于点Q,
则∠OCQ=∠OCB-∠PCB=45?-15?=30?,
在Rt△OCQ中,tan∠OCQ=OQOC=OQ2=33,
∴OQ=233,Q(233,0).
直线CQ的解析式为:y=?3x+2,
联立,得y=?3x+2 y=?x2+x+2,
解得P(3+1,- 3-1) .
②当点P在BC的上方时,
设CP交false轴于点Q,
则∠OCQ=∠OCB+∠PCB=45?+15?=60?,
在Rt△OCQ中,tan∠OCQ=OQOC=OQ2=3,
∴OQ=23,Q(23,0).
直线CQ的解析式为:y=?33x+2,
联立,得y=?33x+2 y=?x2+x+2,
解得P(3+33, ?3+53) .
综上所述:P的坐标为(3+1,- 3-1)或(3+33, ?3+53)
(3)先用“三点特殊位置法”确定动点E的运动路线(注意利用∠CBA=45°),再利用“将军饮马问题”求出最小值时E点的坐标;
当D与B重合时,
则DE⊥AB,且DE=AB,
则E(3,3),
当E与在直线直线上时,
则AE⊥AB,且AE=AB,
则E(-1,3),
则可以确定点E在直线y=3上运动,
作点B关于直线y=3的对称点B`(2,6),
连接AB`,交直线y=3于点E,
此时AE+BE有最小值,
则直线AB`的解析式为:y=2x+2,
当y=3时x=12,∴E(12,3),
即当AE+BE最小时,E(12,3),
∵A(-1,0)、B(2,0)、E(12,3),
①以AB为对角线时,xF=?1+2?12=12yF=0+0?3=?3,∴F(12,-3);
②以AE为对角线时,xF=?1+12?2=?52yF=0+3?0=3 ,∴F(?52,3);
③以BE为对角线时,xF=2+12?(?1)=72yF=0+3?0=3 ,∴F(72,3)
综上所述,当AEBE取最小值时,若以A ,B ,E ,F为顶点的四边形是平行四边形,E(12,3),F点的坐标为(12,-3)、(?52,3)或(72,3)
9.如图 1,抛物线y=mx2?3mx+n与x轴交于点( -1,0),与y轴交于点B(0,3 ) ,在线段OA上有一动点E (不与O 、A重合),过点E作x轴的垂线交直线AB于点N,交抛物线于点P.
(1)分别求出抛物线和直线 AB 的函数表达式;
(2)连接PA 、PB ,求△PAB面积的最大值,并求出此时点P的坐标;
(3)如图 2,点 E(2,0),将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E`A 、E`B,求E`A+23E`B的最小值
【解析】:
(1)∵抛物线y=mx2?3mx+n与x轴交于点(-1,0),与y轴交于点B(0,3),
则有n=3 m+3m+n=0,
解得m=?34n=3 ,
∴抛物线解析式为:y=?34x2+94x+3,
令y=0,则?34x2+94x+3=0,
解得x=4或x=-1,
∴A(4,0),B(0,3),
设直线AB的解析式为y=kx+b,则b=3 4k+b=0 ,
解得k=?34b=3 ,
∴直线AB的解析式为y=?34x+3
(2)如图1中,设P(x, ?34x2+94x+3),
则N(x, ?34x+3) ,
则设△PAB的面积为S,
则S=S?PNA+S?PNB=12PN?OA=12×4×?34x2+94x+3+34x?3=?32x2+6x=?32x?22+6,
∵?32<0,S随x的增大而减小,
∴当x=2时,S有最大值,且最大值为6,
此时P点坐标为(2,92)
(3)点E在圆上运动,故是“阿氏圆”问题,构造“共角模型”的相似三角形关键在于:使半径成为比例中项;
如图2中,在y轴上取一点M′ ,
使得OM′ =43,
连接 AM′,
在AM′上取一点E′,使得OE`=OE.
∵OE′ = 2,OM`?OB=43×3=4,
∴OE`2=OM`?OB,
∴OE`OM`=OBOE`,
∵∠BOE`=∠E`OB,
∴△M`OE`∽△E`OB,
∴M`E`BE`=OE`OB=23,
∴M`E`=23BE`,
∴AE`+23BE`=AE`+E`M`=AM`,
此时AE` +23BE ′最小(两点间线段最短,A、M′、E′共线时),
最小值=AM`=42+(43)2=4103
10.已知二次函数y=ax2+bx+c的图像与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C(0,-3).
(1)求二次函数的解析式;
(2)D是二次函数图像上位于第三象限内的点,求点D到直线AC的距离最大值时点D的坐标;
(3)M是二次函数图像对称轴上的点,在二次函数图像上是否存在点N,使以M、N、B、O为顶点的四边形是平行四边形?若有,请直接写出点N的坐标
【解析】
(1)设二次函数解析为交点式:y=a(x+3)(x-1),
代入C点坐标,
可得a=1,
∴y=(x+3)(x-1)= x2+2x?3
(2)由于AC是固定长,
当D到直线AC的距离最大时,
此时△DAC的面积最大,
设直线AC的解析式为y=kx+b,
代入A,C两点坐标可得k=-1,b=-3,
∴直线AC的解析式为y=-x-3,
作DG//y轴交AC于点G,
设D(a, a2+2a?3),
则G(a,-a-3),
∴DG=-a-3-(a2+2a?3)=? a2?3a,
则S?ACD=12OC?DG=12×3? a2?3a=?32(a+32)2+278,
当a=?32时S?ACD有最大值,
即D到直线AC的距离最大,
此时D点坐标为(?32,?154).
(3)此题正确的方法是代数法
由题可知O(0,0),B(1,0),设M(-1,a)
①当OB为平行四边形对角线时,xN=xO+xB?xM=2 ,
把x=2代入二次函数解析式中,得y=-5,
∴N(2,-5),;
②当OM为平行四边形对角线时,xN=xO+xM?xB=?2 ,
把x=-2代入二次函数解析式中,得y=-3,
∴N(-2,-3),
③当BM为平行四边形对角线时,xN=xB+xM?xO=0 ,
把x=0代入二次函数解析式中,得y=-3,
∴N(0,-3),
综上所述,N的坐标为(2,-5)、(-2,-3)或(2,5)
11.如图1,已知抛物线y=-false(x+3)(x-4false)与x轴交于A、B两点,与false轴交于点C.
(1)(3分)写出A、B、C三点的坐标.
(2)(4分)若点P为△OBC内一点,求OP+BP+CP的最小值.
(3)(3分)如图2,点Q为对称轴左侧抛物线上一动点,点D(4,0),直线DQ分别与y轴、
直线AC交于E、F两点,当△CEF为等腰三角形时,请直接写出CE的长.
2324100142875504825133350
【解析】
(1)当-false(x+3)(x-4false)=0,
解得x=-3或43,
∴A(-3,0),B(43,0),
当x=0时,y=?39×3×?43=4,
∴C(0,4).
(2)小题的解题过程:
由OB、OC的长可得∠OBC=30?,
则∠OBC`=90?,
由OC=4,OB=43,
可得BC`=BC=8,
由勾股定理可得最小值OC`=47,
(3)分三种情况一一论证,解题时,一定要利用好分类讨论题型的特征(一种情况简单、一种情况中等、一种情况较难),每一种先画出草图,再确定由易到难的顺序依次解答,至少要得到2分,
当CE=CF时,如图1;当CE=EF时,如图2;当EF=FC时,如图3;由于等腰三角形添辅助线首先会联想到“三线合一”,即作底边的垂线,而图3的垂线是往坐标轴作,故更符合平常解等腰三角形的图形习惯,故先解图3,其余按图3的添辅助线方法及解题思路过程解答,这样解题的速度会快很多。
①当EF=FC时,如图3,
作FM⊥EC于点M,
则EM=MC,
设EM=MC=a,
由MF//OA
可得MF:OA=CM:OC,
即MF:3=a:4,
可得MF=34a,
由MF//OD
可得MF:OD=EM:OE,
即34a:4=a:(4+2a),
解得a=23,
则CE=2a=43
②当CE=CF时,如图1;
作FM⊥EC于点M,
设CE=CF=m,
由OA=3,OC=4
可得CF=5,
由MF//OA
可得CM:OC=MF:OA=CF:CA,
即CM:4=MF:3=m:5,
可得CM=45m,MF=35m,
由MF//OD
可得MF:OD=ME:OE,
即ME:(4-m)=35m:4=320m,
∴ME=3m(4?m)20,
由OE+ME+CM=OC=4可列方程为:
4-m+3m(4?m)20+45m=4,
解得m=83,
则CE=83
③当CE=EF时,如图2,
作FM⊥EC于点M,但按上述思路解,计算量太大,放弃,思考代数方法。
作AG//DF交y轴于点G,如图4,
由△ECF是等腰,
易得△GAC也是等腰,
设OG=n,
则AG=CG=4-n,
在Rt△OAG中,由勾股定理可得:32+n2=(4?n)2,
解得n=78,
则G(0, 78),
由A、G坐标可得直线AG的解析式为y=724x+78,
由AG//DF可设直线DF的解析式为y=724x+b,
代入D点坐标可得址DF的解析式为724x?76,
∴E(0, ?76),
∴OE=76,
∴CE=316
综上所述,CE的长度为43、83或316.
【思路方法】
1.总体解题思路
left-635
2.总体解题方法
(1)代数论证方法
(2)几何论证方法
3.具体思考角度
【点】
①交点→→联立方程解答;
②图像上的点→→代入法或依解析式设点的坐标;
③中点→→中点坐标公式;
【直线】
①正常情况→→“待定系数法”
②平行线→→K值相等;
③垂直线→→K值负倒数;
【线段】
①点的坐标表示水平或垂直线段→→一定遵循“右减左、上减下”原则,不明确时加上绝对值;
②利用两点间的距离公式表示或计算线段长度;
③利用有关几何性质表示或计算线段长度;
④距离或高→→点到直线的距离公式:
如P(m,n)到直线y=kx+b的距离或高,先把直线的函数表达式变形为方程形式:kx-y+b=0,代入公式
公式:d=|km?n+b|1+k2
⑤线段比或线段积→利用相似三角形性质转化
【角】
①三角函数→→Rt△→→“一线三垂直模型”
②等角性质→→如等边对等角、平行、全等或相似性质等
③和差倍分角→→首先转化成某角的具体度数或一对等角;
【三角形】
①等腰三角形→→一定要结合“边(腰)相等”、“底边三线合一”这两性质展开分析思考;
②直角三角形→→一定要利用好直角走 “一线三垂直模型”、“垂直k值负倒数”、 “勾股定理”等思路;
③三角形相似→→一定要抓住相似性质“对应边成比例”、“对应角相似”、“面积比等于相似比平方”等思路;
【特殊四边形】
①平行四边形
代数→→对角线平行+中点坐标公式;
几何:→→作垂线,走全等;
②菱形
代数→→对角线平行+中点坐标公式+邻边相等;
几何:→→对角线垂直,走Rt△+邻边相等;
③矩形
代数→→对角线平行+中点坐标公式+邻边垂直;
几何:→→对角线相等,走Rt△;
【最值】
①单一线段最值
代数→→字母表示,走二次函数配方;
几何:→→①三个特殊位置法,走点到直线距离;②转化成将军饮马问题;
②线段和差(周长)最值
代数→→字母表示,走二次函数配方;
几何:→→①三个特殊位置法,走点到直线距离;②转化成将军饮马问题;
③面积最值
代数→→字母表示,走二次函数配方;
几何:→→转化成高或底的线段最值问题;
④定值
代数→→字母表示,约分成具体数值;
几何:→→利用相似等几何性质,转化成与已知线段相联系;
【面积方法】→→“铅垂法”、“割补法”、“公式法”、“相似的面积比或不相似时平行线间的底之比”
【强化巩固练习】
1.在平面直角坐标系中,抛物线y=ax2+bx+c经过点A、B、C,已知A(-1,0),B(6,0),C(0,-6).
(1)求此抛物线的函数表达式;
(2)若点D为第四象限内抛物线上一动点,当△BCD面积最大时,求△BCD面积最大值;
(3)在x轴上是否存在点M,使∠OCM+∠ACO=45°,若存在,请求出点M的坐标;若不存在,请说明理由.
2.如图1,抛物线y=14x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴负半轴交于点C,OC=OB=10.
(1)求抛物线解析式;
(2)点P,Q在第四象限内抛物线上,点P在点Q下方,连接CP,CQ,∠OCP+∠OCQ=180°,设点Q的横坐标为m,点P的横坐标为n,求m与n的函数关系式;
(3)如图2,在(2)的条件下,连接AP交CO于点D,过点Q作QE⊥AB于点E,连接BQ,DE,是否存在点P,使∠AED=2∠EQB,若存在,求出点P的坐标;若不存在,请说明理由。
3. 已知抛物线y=ax2?3ax?4a(a<0)与x轴交于A,B两点,与y轴交于C点.
(1)若a=-1时.
①求A、B、C三点的坐标;
②如图1,点P是直线BC上方抛物线上一点,过P点作PF//y轴交BC于F点,若S?PFCS?OFC=34,请求出P点坐标;
(2)如图2,将△AOC绕原点O顺时针旋转得△DOE,且使得点D落在线段AC上.当OE⊥BC时,请求出a的值和CE的长.
4.如图1,抛物线y=ax2+bx+c与x轴点A(-1,0),B(3,0),与y轴交于点C,∠CAB=60°,点E是线段AB上一动点,作EF//AC交线段BC于点F.
(1)求抛物线解析式;
(2)如图1,延长线段EF交抛物线第二象限的部分于点G,点D是AC边中点,当四边形ADGF为平行四边形时,求出G点坐标;
(3)如图2,M为射线EF上一点,且EM=EB,将射线EF绕点E逆时针旋转60°,交直线AC于点N,连接MN,P为MN的中点,连接AP,BP,问:AP+BP是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由。
5.已知抛物线y=ax2?2ax?3a(a≠0)
请直接写出该抛物线的对称轴和顶点坐标;(用含a的代数式表示)
若a>0,且false与false是该抛物线上的两点,且false,求m的取值范围;
如图11,当a=1时,该抛物线 与x轴分别交于A、B两点,与y轴交于点C,D是直线BC下方抛物线上的一个动点,AD交BC于点E,设点E的横坐标为n,记S=S?BDES?ABE,当n为何值时,S取最大值?并求出S的最大值.
6.如图1,抛物线y=ax2+2x+c与x轴交于点A,B,与y轴交于点C(0,3),连接BC,抛物线的对称轴为直线x=1,且与BC交于点D,与x轴交于点E.
(1)求抛物线的解析式;
(2)如图2,把△DEB绕点D顺时针旋转60°得到△DMN,求证:点M在抛物线上;
(3)如图3,点P是抛物线上的动点,连接PN,BN,当∠PNB=30°时,请直接写出直线PN的解析式.
7.在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,﹣2).
(1)求抛物线的函数表达式;
(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,求DEAE的最大值;
(3)如图2,连接AC,BC,过点O作直线l∥BC,点P,Q分别为直线l和抛物线上的点,试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB.若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
8.如图1,直线yx2与x轴交于点B ,与y轴交于点C ,抛物线yax2 bx c(a 0)经过点A, B,C,点A的坐标为(1,0) .
(1)求二次函数yax2 bxc(a0)的表达式;
(2)抛物线的图像上是否存在点P,使得PCB 15 ,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图2,直线BC上有一动点D,连接AD,将线段AD绕点D顺时针旋转90 得到线段DE ,连接AE,BE.当AEBE取最小值时,若以A ,B ,E ,F为顶点的四边形是平行四边形,请直接写出E点和F点的坐标.
9.如图 1,抛物线y=mx2?3mx+n与x轴交于点( -1,0),与y轴交于点B(0,3 ) ,在线段OA上有一动点E (不与O 、A重合),过点E作x轴的垂线交直线AB于点N,交抛物线于点P.
(1)分别求出抛物线和直线 AB 的函数表达式;
(2)连接PA 、PB ,求△PAB面积的最大值,并求出此时点P的坐标;
(3)如图 2,点 E(2,0),将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E`A 、E`B,求E`A+23E`B的最小值
10.已知二次函数y=ax2+bx+c的图像与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C(0,-3).
(1)求二次函数的解析式;
(2)D是二次函数图像上位于第三象限内的点,求点D到直线AC的距离最大值时点D的坐标;
(3)M是二次函数图像对称轴上的点,在二次函数图像上是否存在点N,使以M、N、B、O为顶点的四边形是平行四边形?若有,请直接写出点N的坐标
11.如图1,已知抛物线y=-false(x+3)(x-4false)与x轴交于A、B两点,与false轴交于点C.
(1)(3分)写出A、B、C三点的坐标.
(2)(4分)若点P为△OBC内一点,求OP+BP+CP的最小值.
(3)(3分)如图2,点Q为对称轴左侧抛物线上一动点,点D(4,0),直线DQ分别与y轴、
直线AC交于E、F两点,当△CEF为等腰三角形时,请直接写出CE的长.
2324100142875504825133350
【答案详解】
1.在平面直角坐标系中,抛物线y=ax2+bx+c经过点A、B、C,已知A(-1,0),B(6,0),C(0,-6).
(1)求此抛物线的函数表达式;
(2)若点D为第四象限内抛物线上一动点,当△BCD面积最大时,求△BCD面积最大值;
(3)在x轴上是否存在点M,使∠OCM+∠ACO=45°,若存在,请求出点M的坐标;若不存在,请说明理由.
【解析】
(1)设交点式,代入点B坐标即可得抛物线解析式:y=x2?5x?6
(2) “铅垂法”+配方法解题。
如图1作DE//y轴交BC于点E,
设D(a, a2?5a?6),
由B,C可得直线BC的解析式为y=x-6,
则E(a,a-6),
则DE=a-6-(a2?5a?6)=? a2+6a,
则S?BCD=12OB?DE=12×6? a2+6a=?3a2+18a=? 3a?32++27,
当a=3时,S?BCD有最大值,最大值为27.
(3)二次函数典型题型:点角存在性问题。先把角的和差问题转化成一个角的问题,再按点角存在性问题的典型思路解题。
由B,C两点坐标可知,∠OCB=45?,
①当点M在y轴右侧时,∠OCM+∠ACO=45°,∠OCM+∠BCM=45?,
∴∠ACO=∠BCM,
则tan∠ACO=tan∠BCM=OAOC=16,
作BF⊥BC交CM于点F,过B作GP⊥x轴,作FG⊥GP于点G,作CP⊥GP于点P,
则由“一线三垂直模型”易得△FGB∽△BPC,
则FGBP=GBCP=FBBC=tan∠BCM=16,
∵CP=BP=6,
∴FG=GB=1,
∴F(5,1),
∴直线CF的表达式为y=75x?6,
∴M(307,0)
②作M关于点O的对称点M`,连接CM`,
则∠OCM=∠OCM`,
由∠OCM+∠ACO=45°
可得∠OCM`+∠ACO=45°,
点M`符合题目要求,
则M`(?307,0)
综上所述,点M的坐标为(307,0)或(-307,0)
2.如图1,抛物线y=14x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴负半轴交于点C,OC=OB=10.
(1)求抛物线解析式;
(2)点P,Q在第四象限内抛物线上,点P在点Q下方,连接CP,CQ,∠OCP+∠OCQ=180°,设点Q的横坐标为m,点P的横坐标为n,求m与n的函数关系式;
(3)如图2,在(2)的条件下,连接AP交CO于点D,过点Q作QE⊥AB于点E,连接BQ,DE,是否存在点P,使∠AED=2∠EQB,若存在,求出点P的坐标;若不存在,请说明理由。
【解析】
(1)由OC=OB=10可得C(0,-10),B(10,0),
代入可得抛物线解析式为:y=14x2?32x?10
(2)作QM⊥y轴交于点M,作PN⊥y轴交于点N,
设Q(m, 14m2?32m?10),P(n, 14n2?32n?10),
∵∠OCP+∠OCQ=180°,∠OCP+∠PCN=180°,
∴∠OCQ=∠PCN,
∴tan∠OCQ=tan∠PCN,
∴MQMC=NPCN,即 m14m2?32m= n?14n2+32n,
整理得:m=-n+12
(3)先把倍角转化为等角,再按点角性问题解题
作EH平分∠AED,则∠EQB=∠AEH,
则tan∠AEH=tan∠EQB=4m+4 ,
由角平分线性质联想到辅助线:作HA⊥x轴交EH于点H,作HM⊥ED交ED延长线于点M,
由对角平分线的对称性质可得AE=EM=m+4,HM=AH=4,
作HN⊥y轴于点N,
则ON=AH=4,HN=OA=4,
由HM=HN=4,DH=DH可证△HND≌△HMD,
可得MD=DN,作PF⊥x轴于点F,
则tan∠FAP=ODOA=PFAF=OD4=?14m2+32m+10n+4=n?10?4,
∴OD=10-n,
∵m=-n+12,
∴OD=m-2,
∴DM=DN=OD-ON=m-6,
∴DE=EM-DM=m+4-(m-6)=10,
在Rt△ODE中,由OE2+OD2=DE2可列方程为:
n2+(10?n)2=102,
即(12?n)2+(10?n)2=102,
解得n=4或18(舍去),
∴P(4,-12)
3. 已知抛物线y=ax2?3ax?4a(a<0)与x轴交于A,B两点,与y轴交于C点.
(1)若a=-1时.
①求A、B、C三点的坐标;
②如图1,点P是直线BC上方抛物线上一点,过P点作PF//y轴交BC于F点,若S?PFCS?OFC=34,请求出P点坐标;
(2)如图2,将△AOC绕原点O顺时针旋转得△DOE,且使得点D落在线段AC上.当OE⊥BC时,请求出a的值和CE的长.
【解析】
(1)①把a=-1代入解析式,分别令x=0和y=0即可求出A,B,C三点的坐标;
②先根据S?PFCS?OFC=34求出PF的值,再求出直线BC的解析式为,设P(m,?m2?3m+4),则F(m,-m+4),然后利用PF=3列方程求解即可;
(2)先证明AB=BC=5,再根据勾股定理求出OC的长,即可求出a的值;过O作OH⊥AD,根据cos∠OAC=AHAO=OAAC,可求出AH,然后利用△AOD∽△COE即可求出CE的值.
解:(1)若a=-1时
①原抛物线为y=?x2+3x+4,
当x=0时,y=4,
即C(0,4),
当y=0时,即?x2+3x+4=0时,
∴(x+1)(x-4)=0,
解得x1=?1,x2=4,
即A(-1,0),B(4,0);
②∵PF//y,
∴S?PFCS?OFC=PFOC=34,
∵OC=4,
∴PF=3,
设直线BC的解析式为:y=kx+b,
把B(4,0),C(0,4)代入,
得4k+b=0b=4 ,
∴b=4 k=?1,
∴y=-x+4,
设P(m,?m2?3m+4),
则F(m,-m+4),
∴PF=?m2?3m+4??m+4=?m2+4m=3,
解得m1=1,m2=3,
当m=1时,-m2+3m+4=-1+3+4=6;
当m=3时,-m2+3m+4=-9+9+4=4;
∴P1(1,6),P2(3,4);
(2)由旋转的性质得:OA=OD,∠DOE=∠AOC=90°,
∵OE⊥BC,
∴OD//BC,
∴∠DAO=∠ADO=∠ACB
,∴BA=BC=4+1=5,
∴OC=52?42=3,AC=12+32=10,
即OC=-4a=3,
∴a=-34.
过O作OH⊥AD,则cos∠OAC=AHAO=OAAC,
∴AH1=110,
∴AH=DH=1010,
∴AD=105.
由旋转的性质得,OA=OD,OC=OE,
∴OAOD=OCOE=1,
∵∠AOD+∠COD=90°,∠COE+∠COD=90°,
∴∠AOD=∠COE,
∴△AOD∽△COE,
∴ADCE=OAOC,
∵a=-34,
∴y=?34x2+94x+3,
当x=0时,y=3,
即C(0,3),
当y=0时,即?34x2+94x+3=0时,
∴(x+1)(x-4)=0,
解得x1=?1,x2=4,
即A(-1,0),B(4,0);
∴OA=1,OC=3,
∴ADCE=OAOC=13,
∴CE=3105.
4.如图1,抛物线y=ax2+bx+c与x轴点A(-1,0),B(3,0),与y轴交于点C,∠CAB=60°,点E是线段AB上一动点,作EF//AC交线段BC于点F.
(1)求抛物线解析式;
(2)如图1,延长线段EF交抛物线第二象限的部分于点G,点D是AC边中点,当四边形ADGF为平行四边形时,求出G点坐标;
(3)如图2,M为射线EF上一点,且EM=EB,将射线EF绕点E逆时针旋转60°,交直线AC于点N,连接MN,P为MN的中点,连接AP,BP,问:AP+BP是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由。
【解析】
(1)设抛物线交点式y=a(x+1)(x-3),
∵tan∠CAB=OCOA=tan60°,
∴OC=3,
∴C(0, 3),
把C点坐标代入解析式中,得a=?33,
∴抛物线解析式为y=?33x+1x?3=?33x2+233x+3;
(2)由题可得:AC2=4,BC2=12,AB2=16,
∵AC2+BC2=AB2,
∴∠ACB=90°, ∠ABC=30°,
由D是AC的中点可得AD=1,
当四边形ADGF为平行四边形时,AD=FG=1,AD//FG,
∴∠GFB=90°,
如图构造“一线三垂直模型”,则可得∠ABC=∠HFG=30°,
∴HG=12,FH=32 ,
设G(a, ?33a2+233a+3),
则F(a-12, ?33a2+233a+32),
由B,C两点坐标可得直线BC的解析为:y=?33x+3,
∵F在BC上,
∴?33a?12+3=?33a2+233a+32,
解得a=2或a=1,
∴G(1,433)或(2, 3)
(3)由题易证△ANE、△BEM均是等边三角形,
设E(m,0),则AE=m+1,BE=3-m,
则等边三角形性质“高=边长×32”
可得N(m?12, 3(m+1)2),M(3+m2, 3(3?m)2),
∵P是MN的中点,由中点坐标公式可得P(m+12, 3),
当E与A重合时N与A重合,
M在射线AC上,且AM=AB=4,
∵AC=2,故P0与C重合,
当E运动到AB中点时,AE=BE=2,
此时等边△ANE与等边△BEM全等,
这是点E的运动终点,
此时PE⊥x轴,P1 (1, 3),
点P就在线段P0P1间运动,
即P点在y轴与抛物线对称轴间的垂直于C点的线段y=3上运动,
作点A关于直线y=3的对称点A`(-1,23)false
连接A`B交直线y=3于点P,
此时,AP+BP=A`B=2 7.
5.已知抛物线y=ax2?2ax?3a(a≠0)
请直接写出该抛物线的对称轴和顶点坐标;(用含a的代数式表示)
若a>0,且false与false是该抛物线上的两点,且false,求m的取值范围;
如图11,当a=1时,该抛物线 与x轴分别交于A、B两点,与y轴交于点C,D是直线BC下方抛物线上的一个动点,AD交BC于点E,设点E的横坐标为n,记S=S?BDES?ABE,当n为何值时,S取最大值?并求出S的最大值.
【解析】
(1)对称轴是直线x=1;顶点坐标为(1,-4a).
(2)∵a>0,∴当x≥1时,y随x的增大而增大.
①当点P位于对称轴的右侧,即当m>1时,
∵y1>y2,
∴m>5;
②当点P位于对称轴的左侧,即当m<1时,
作点P关于对称轴的对称点Q,
则Q(2-m, y1),
∵y1>y2,
∴2-m>5,
解得m<-3;
∴m的取值范围是m<-3或m>5.
(3)当a=1时抛物线的解析式为y=x2?2x?3.
当y=0时x2?2x?3=0,
解得x1=3,x2=?1,
∴A(-1,0),B(3,0),
当x=0时y=-3,
∴C(0,-3),
∴直线BC的解析式为:y=x-3.
过点A作AF//y轴交直线BC于点F,作HD//y轴交直线BC于点G,交x轴于点D,
则△DEG∽△AEF,
∴S=S?BDES?ABE=DEAE=DGAF,
∵A(-1,0),
∴F(-1,4),
∴AF=4,
设D(a,a2?2a?3),
则G(a,a-3),
∴DG=a-3-(a2?2a?3)=?a2+3a,
∴S=?a2+3a4=?14(a?32)2+916,
∵?14<0,
∴当a=32时,S有最大值,且最大值为916,
此时点D的坐标为(32,?154).
∴直线AD的解析式为:y=-32x-32,
联立方程y=?32x?32y=x?3 ,
解得x=35y=?45,∴n=35.
∴当n=35时,S取最大值,最大值为916.
6.如图1,抛物线y=ax2+2x+c与x轴交于点A,B,与y轴交于点C(0,3),连接BC,抛物线的对称轴为直线x=1,且与BC交于点D,与x轴交于点E.
(1)求抛物线的解析式;
(2)如图2,把△DEB绕点D顺时针旋转60°得到△DMN,求证:点M在抛物线上;
(3)如图3,点P是抛物线上的动点,连接PN,BN,当∠PNB=30°时,请直接写出直线PN的解析式.
【解析】
(1)由对称轴x=1可知?b2a=?1a=1,
则a=-1,
由C点坐标可得c=3,
∴抛物线解析式为y=?x2+2x+3
(2)由抛物线解析式可知,
当y=0时?x2+2x+3=0
,解得x1=?1,x2=3,
∴A(-1,0),B(3,0),
由C(0,3),B(3,0)可得直线BC的解析式为y=-x+3,
则D(1,2),E(1,0),
则DE=2,
由旋转性质可得∠MDE=60°,MD=DE=2,
延长DM交x轴交于点G,作MH⊥x轴于点H,
则∠G=30°,
在Rt△GDE中由DE=2,
可得GD=4,DE=23,
则GM=2,
由MH//DE
可得GH:GE=MH:DE=GM:GD=2:4,
则可得MH=1,EH=3,
∴OH=3?1,
∴M(1-3,1),
当x=1-3时?x2+2x+3=?1?32+21?3+3=1,
∴点M在抛物线上;
(3)如图5,过点M作QR⊥x轴,作DQ⊥QR于Q,作NR⊥QR于点R,
由题可知△DEB为等腰直角三角形,
则△MDN是等腰直角三角形,
则△DQM≌△MRN,
则MR=DQ=3,RN=MQ=1,
∴N(2?3, 1?3),
由题可知DB=DN,∠BDN=60°,
∴△DNB是等边三角形,
①当P点在B点上方时,
∵∠PNB=30°,
由等边三角形“三线合一”性质可知NP垂直平分线段DB,
则题可知△EDB是等腰直角三角形,
∴E点在线段BD的垂直平分线NP上,
由N、E的坐标可得直线NP的解析式为y=x-1;
②当P点在B点下方时,
∵∠PNB=30°,∠DNB=60°,
∴∠DNP=90°,
由D、N两点坐标可得直线DN的解析式为:y=2+3x?3,
∴设直线NP的解析式为y=?2+3x+b,
代入N点坐标可得b=8-53,
∴直线NP的解析式为y=?2+3x+8?53,
综上所述,直线PN的解析式为y=x-1或y=?2+3x+8?53
7.在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,﹣2).
(1)求抛物线的函数表达式;
(2)如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,求DEAE的最大值;
(3)如图2,连接AC,BC,过点O作直线l∥BC,点P,Q分别为直线l和抛物线上的点,试探究:在第一象限是否存在这样的点P,Q,使△PQB∽△CAB.若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
【解析】(1)设抛物线为交点式,
即y=a(x+1)(x-4),
代入C点坐标,
可得a=12,
∴抛物线解析式为y=12(x+1)(x-4)=12x2?32x?2
(2)构造相似典型图形“8字模型”,利用相似性质把DEAE用代数式表示出来,再利用二次函数配方法求最值。
作KA⊥x轴交直线BC于点K,作DG⊥x轴于点G,交直线BC于点F,
由B(4,0)、C(0,-2)可得直线BC的解析式为:y=12x-2,
则K(-1,-52),
则AK=52,
设D(a, 12a2?32a?2),
则F(a, 12a-2),则DF=12a-2-(12a2?32a?2)=?12a2+2a,
∵DF//AK,
∴DEAE=DFAK=?12a2+2a52=?15a2+45a=?15a?22+45,
即当a=2时,DEAE有最大值为45.
(3)由题可知:AC2=5,BC2=20,AB2=25,
∵AC2+BC2=AB2,
∴∠ACB=90°,
当△PQB∽△CAB时,
∠QPB=∠ACB=90°,BPQP=BCAC=205=2,
构造“一线三垂直模型”可求解点P的坐标;
又∵直线l∥BC,
∴直线l的表达式为y=12x.
①当P在Q点右侧时,如图,
过P作MN⊥x轴于N,作QM⊥MN于点M,
则△QMP∽△PNB,
∴BNMP=PNQM=BPQP=2
设P(2m,m),
则BN=2m-4,PN=m,
∴QM=12m,MP=m-2,
∴Q点坐标为(32m,2m-2),
将 Q点坐标代入抛物线解析式中得12×(32m)2?32×(32m)?2=2m?2,
解得m=349或m=0(舍去),
∴P点坐标为(689,349);
②当P在Q点左侧时,如图,
过P作MN⊥x轴于N,作QM⊥MN于点M,
则△QMP∽△PNB,
∴BNMP=PNQM=BPQP=2
设P(2m,m),
则BN=4-2m,PN=m,
∴QM=12m,MP=2-m,
∴Q点坐标为(52m,2),
将 Q点坐标代入抛物线解析式中得12×(52m)2?32×(52m)?2=2,
解得m=3+415或m=3?415 (舍去),
∴P点坐标为(6+2415,3+415);
综上所述,P的坐标为(689,349)或(6+2415,3+415)
8.如图1,直线yx2与x轴交于点B ,与y轴交于点C ,抛物线yax2 bx c(a 0)经过点A, B,C,点A的坐标为(1,0) .
(1)求二次函数yax2 bxc(a0)的表达式;
(2)抛物线的图像上是否存在点P,使得PCB 15 ,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图2,直线BC上有一动点D,连接AD,将线段AD绕点D顺时针旋转90 得到线段DE ,连接AE,BE.当AEBE取最小值时,若以A ,B ,E ,F为顶点的四边形是平行四边形,请直接写出E点和F点的坐标.
【解析】
(1)∵直线y=-x+2与x轴交于点B,与y轴交于点C,
∴B(2,0),C(0,2) .
∵抛物线交x轴于A,B两点,
∴设抛物线解析式为y=a(x+1)(x-2).
代入点C(0,2),
解得a=-1,
∴抛物线解析式为y=?x+1x?2=?x2+x+2.
(2)分以下两种情况:
①当点P在BC的下方时,
设CP交x轴于点Q,
则∠OCQ=∠OCB-∠PCB=45?-15?=30?,
在Rt△OCQ中,tan∠OCQ=OQOC=OQ2=33,
∴OQ=233,Q(233,0).
直线CQ的解析式为:y=?3x+2,
联立,得y=?3x+2 y=?x2+x+2,
解得P(3+1,- 3-1) .
②当点P在BC的上方时,
设CP交false轴于点Q,
则∠OCQ=∠OCB+∠PCB=45?+15?=60?,
在Rt△OCQ中,tan∠OCQ=OQOC=OQ2=3,
∴OQ=23,Q(23,0).
直线CQ的解析式为:y=?33x+2,
联立,得y=?33x+2 y=?x2+x+2,
解得P(3+33, ?3+53) .
综上所述:P的坐标为(3+1,- 3-1)或(3+33, ?3+53)
(3)先用“三点特殊位置法”确定动点E的运动路线(注意利用∠CBA=45°),再利用“将军饮马问题”求出最小值时E点的坐标;
当D与B重合时,
则DE⊥AB,且DE=AB,
则E(3,3),
当E与在直线直线上时,
则AE⊥AB,且AE=AB,
则E(-1,3),
则可以确定点E在直线y=3上运动,
作点B关于直线y=3的对称点B`(2,6),
连接AB`,交直线y=3于点E,
此时AE+BE有最小值,
则直线AB`的解析式为:y=2x+2,
当y=3时x=12,∴E(12,3),
即当AE+BE最小时,E(12,3),
∵A(-1,0)、B(2,0)、E(12,3),
①以AB为对角线时,xF=?1+2?12=12yF=0+0?3=?3,∴F(12,-3);
②以AE为对角线时,xF=?1+12?2=?52yF=0+3?0=3 ,∴F(?52,3);
③以BE为对角线时,xF=2+12?(?1)=72yF=0+3?0=3 ,∴F(72,3)
综上所述,当AEBE取最小值时,若以A ,B ,E ,F为顶点的四边形是平行四边形,E(12,3),F点的坐标为(12,-3)、(?52,3)或(72,3)
9.如图 1,抛物线y=mx2?3mx+n与x轴交于点( -1,0),与y轴交于点B(0,3 ) ,在线段OA上有一动点E (不与O 、A重合),过点E作x轴的垂线交直线AB于点N,交抛物线于点P.
(1)分别求出抛物线和直线 AB 的函数表达式;
(2)连接PA 、PB ,求△PAB面积的最大值,并求出此时点P的坐标;
(3)如图 2,点 E(2,0),将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E`A 、E`B,求E`A+23E`B的最小值
【解析】:
(1)∵抛物线y=mx2?3mx+n与x轴交于点(-1,0),与y轴交于点B(0,3),
则有n=3 m+3m+n=0,
解得m=?34n=3 ,
∴抛物线解析式为:y=?34x2+94x+3,
令y=0,则?34x2+94x+3=0,
解得x=4或x=-1,
∴A(4,0),B(0,3),
设直线AB的解析式为y=kx+b,则b=3 4k+b=0 ,
解得k=?34b=3 ,
∴直线AB的解析式为y=?34x+3
(2)如图1中,设P(x, ?34x2+94x+3),
则N(x, ?34x+3) ,
则设△PAB的面积为S,
则S=S?PNA+S?PNB=12PN?OA=12×4×?34x2+94x+3+34x?3=?32x2+6x=?32x?22+6,
∵?32<0,S随x的增大而减小,
∴当x=2时,S有最大值,且最大值为6,
此时P点坐标为(2,92)
(3)点E在圆上运动,故是“阿氏圆”问题,构造“共角模型”的相似三角形关键在于:使半径成为比例中项;
如图2中,在y轴上取一点M′ ,
使得OM′ =43,
连接 AM′,
在AM′上取一点E′,使得OE`=OE.
∵OE′ = 2,OM`?OB=43×3=4,
∴OE`2=OM`?OB,
∴OE`OM`=OBOE`,
∵∠BOE`=∠E`OB,
∴△M`OE`∽△E`OB,
∴M`E`BE`=OE`OB=23,
∴M`E`=23BE`,
∴AE`+23BE`=AE`+E`M`=AM`,
此时AE` +23BE ′最小(两点间线段最短,A、M′、E′共线时),
最小值=AM`=42+(43)2=4103
10.已知二次函数y=ax2+bx+c的图像与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C(0,-3).
(1)求二次函数的解析式;
(2)D是二次函数图像上位于第三象限内的点,求点D到直线AC的距离最大值时点D的坐标;
(3)M是二次函数图像对称轴上的点,在二次函数图像上是否存在点N,使以M、N、B、O为顶点的四边形是平行四边形?若有,请直接写出点N的坐标
【解析】
(1)设二次函数解析为交点式:y=a(x+3)(x-1),
代入C点坐标,
可得a=1,
∴y=(x+3)(x-1)= x2+2x?3
(2)由于AC是固定长,
当D到直线AC的距离最大时,
此时△DAC的面积最大,
设直线AC的解析式为y=kx+b,
代入A,C两点坐标可得k=-1,b=-3,
∴直线AC的解析式为y=-x-3,
作DG//y轴交AC于点G,
设D(a, a2+2a?3),
则G(a,-a-3),
∴DG=-a-3-(a2+2a?3)=? a2?3a,
则S?ACD=12OC?DG=12×3? a2?3a=?32(a+32)2+278,
当a=?32时S?ACD有最大值,
即D到直线AC的距离最大,
此时D点坐标为(?32,?154).
(3)此题正确的方法是代数法
由题可知O(0,0),B(1,0),设M(-1,a)
①当OB为平行四边形对角线时,xN=xO+xB?xM=2 ,
把x=2代入二次函数解析式中,得y=-5,
∴N(2,-5),;
②当OM为平行四边形对角线时,xN=xO+xM?xB=?2 ,
把x=-2代入二次函数解析式中,得y=-3,
∴N(-2,-3),
③当BM为平行四边形对角线时,xN=xB+xM?xO=0 ,
把x=0代入二次函数解析式中,得y=-3,
∴N(0,-3),
综上所述,N的坐标为(2,-5)、(-2,-3)或(2,5)
11.如图1,已知抛物线y=-false(x+3)(x-4false)与x轴交于A、B两点,与false轴交于点C.
(1)(3分)写出A、B、C三点的坐标.
(2)(4分)若点P为△OBC内一点,求OP+BP+CP的最小值.
(3)(3分)如图2,点Q为对称轴左侧抛物线上一动点,点D(4,0),直线DQ分别与y轴、
直线AC交于E、F两点,当△CEF为等腰三角形时,请直接写出CE的长.
2324100142875504825133350
【解析】
(1)当-false(x+3)(x-4false)=0,
解得x=-3或43,
∴A(-3,0),B(43,0),
当x=0时,y=?39×3×?43=4,
∴C(0,4).
(2)小题的解题过程:
由OB、OC的长可得∠OBC=30?,
则∠OBC`=90?,
由OC=4,OB=43,
可得BC`=BC=8,
由勾股定理可得最小值OC`=47,
(3)分三种情况一一论证,解题时,一定要利用好分类讨论题型的特征(一种情况简单、一种情况中等、一种情况较难),每一种先画出草图,再确定由易到难的顺序依次解答,至少要得到2分,
当CE=CF时,如图1;当CE=EF时,如图2;当EF=FC时,如图3;由于等腰三角形添辅助线首先会联想到“三线合一”,即作底边的垂线,而图3的垂线是往坐标轴作,故更符合平常解等腰三角形的图形习惯,故先解图3,其余按图3的添辅助线方法及解题思路过程解答,这样解题的速度会快很多。
①当EF=FC时,如图3,
作FM⊥EC于点M,
则EM=MC,
设EM=MC=a,
由MF//OA
可得MF:OA=CM:OC,
即MF:3=a:4,
可得MF=34a,
由MF//OD
可得MF:OD=EM:OE,
即34a:4=a:(4+2a),
解得a=23,
则CE=2a=43
②当CE=CF时,如图1;
作FM⊥EC于点M,
设CE=CF=m,
由OA=3,OC=4
可得CF=5,
由MF//OA
可得CM:OC=MF:OA=CF:CA,
即CM:4=MF:3=m:5,
可得CM=45m,MF=35m,
由MF//OD
可得MF:OD=ME:OE,
即ME:(4-m)=35m:4=320m,
∴ME=3m(4?m)20,
由OE+ME+CM=OC=4可列方程为:
4-m+3m(4?m)20+45m=4,
解得m=83,
则CE=83
③当CE=EF时,如图2,
作FM⊥EC于点M,但按上述思路解,计算量太大,放弃,思考代数方法。
作AG//DF交y轴于点G,如图4,
由△ECF是等腰,
易得△GAC也是等腰,
设OG=n,
则AG=CG=4-n,
在Rt△OAG中,由勾股定理可得:32+n2=(4?n)2,
解得n=78,
则G(0, 78),
由A、G坐标可得直线AG的解析式为y=724x+78,
由AG//DF可设直线DF的解析式为y=724x+b,
代入D点坐标可得址DF的解析式为724x?76,
∴E(0, ?76),
∴OE=76,
∴CE=316
综上所述,CE的长度为43、83或316.
同课章节目录
