南昌万淑明13.3 实 数(第一课时)
文档属性
| 名称 | 南昌万淑明13.3 实 数(第一课时) |  | |
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-22 22:22:55 | ||
图片预览







文档简介
(共24张PPT)
数 的 扩 充
—— 13.3 实 数(第一课时)
关于数的分类整理(一)
问题1:说出下面各列数的名称
(整数)
(分数)
(有限小数和无限循环小数)
问题2:说出问题1中的三列数,它们共同的名称
(有理数)
它们均可化为分数
有理数的新认识
1.有理数的特征
注意:
(整数可以看成是小数部分是0的小数)
整数与有限小数的关系.
分数与有限小数或无限循环小数的关系.
(有限小数或无限循环小数可以看成是分数)
2.有理数的特征也可以这样理解:
见课本P82:任何一个有理数都可以写成有限小数或无限循环小数;反过来,任何有限小数或无限循环小数也都是有理数
可以写成: 形式的数叫有理数
关于数的分类整理(二)
问题1:观察下面各列数的特征
(1)
(2)
e是自然对数的底,e=2.718281828……
是圆周率,
它们都是无限不循环小数)
(相邻两个3之间的7的个数逐次加1)
(3)
(本学期我们学方根和立方根,当然还有4次方根、 5次方根、n次方根,而这些数中有一些是有理数,还有一些不是有理数,即它们不是有限数、也不是无限循环的小数,它们是无限不循环的小数,)
(我们学过的数中,有一些是构造出来的无限不循环的无限小数),这此无限不循环的小数究竟是什么数?叫什么数呢?
(我们学过的数中,有一些含 ,含e的无限不循环的无限小数)
数的扩充
上面观察到的那些数中,无限不循环小数,
数学家给这些数取名为叫
无理数.
不能写成:
形式的数叫无理数.
无理数另一种说法
实数的认识
(1)有理数(有限数或无限循环小数)
可以写成: 形式的数
(2)无理数(无限不循环的无限小数)
不能写成:
形式的数
有理数与无理数统称为实数
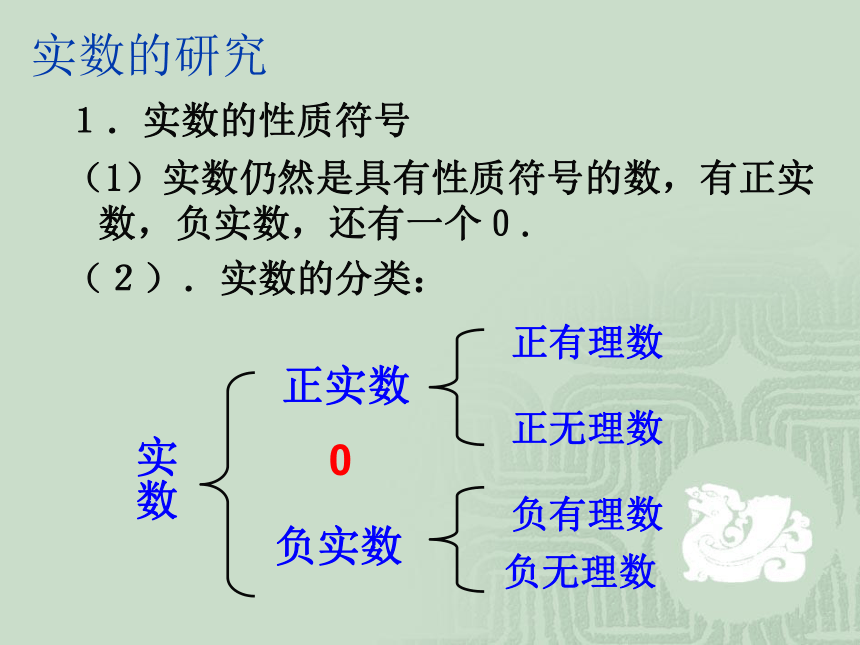
实数的研究
(1)实数仍然是具有性质符号的数,有正实数,负实数,还有一个0.
(2).实数的分类:
1.实数的性质符号
实数
正实数
0
负实数
负有理数
负无理数
正无理数
正有理数
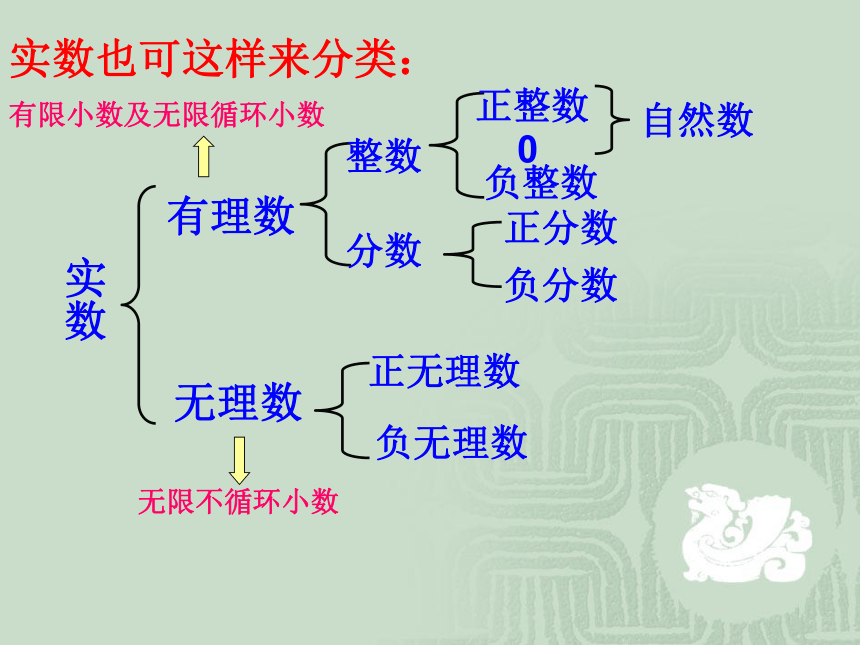
实数
有理数
无理数
正分数
负分数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
自然数
实数也可这样来分类:
分数
整数
正整数
0
负整数
例1:把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
2.实数与数轴上的点的关系
(1)有理数与数轴上的点有对应关系
0
1
2
4
3
-1
-2
每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢?
实数的研究
0
1
2
4
3
-1
-2
π
我们将直径为1的圆上一点与数轴上原点重合,并沿数轴向右滚动,我们来观察结果:
(2)无理数与数轴上的点有对应关系
实数的研究
你能在数轴上找到表示 这样的无理数的点吗?
这个无理数就在数轴上找到了相应的点表示了.
π
问题3:
0
1
2
4
3
-1
-2
问题4:边长为1的正方形,对角线长为多少 你能在数轴上找到表示这个数的点吗?还能找到表示这个数的相反数的点吗?
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.无论是表示有理的点或是表示无理数的点都是表示实数的点
实数与数轴上的点是一一对应的.
(1)有理数与轴上的点有对应关系
(2)无理数也能用数轴上的点来表示其对应关系
归纳
3.平面直角坐标系中的点与有序实数对的关系
(1)由有理数组成的有序数对与平面直角坐标系中的点对应
关系 P(-2,3)、Q( 3 ,1/3)
(2)由无理数组成的有序
数对与平面直角坐标系中的点
对应关系
(3)由有理数、无理数组成的
有序数对与平面直角坐标系
中的点对应关系
有序实数对与平面直角坐标系
中的点是一 一对应的
O
x
y
归纳
无理数的自画像
我们无理数是实数中的一员,都是无限小数,并且是无限不循环小数,鉴定我们的方法不少,带根号的一定是我们无理数, 也就是说我们一定
带有根号,两个无理数之积不一定是无理数,但我们两个无理数之和一定是无理数,不能用分数表示出的就是我们无理数,否则可以用分数表示出来的就是我的好朋友有理数了.
以上说法你认为正确吗?
1.下列关于实数的说法正确是( )
(A) 无理数就是开方开不尽的数
(B)无理数是无限小数
(C)无理数包括正无理数、0、负无理数
(D)无理数都可以用数轴上的点来表示,无限小数都是 无理数
A
D
A
练一练
例2:比较下列各组实数的大小
(1)-3与-5;
(2)
(3)
(4)如图,点A、B表示实数a、b,试比较
a、-a、b、-b的大小.
-a
-b
0
a
b
B
A
解:b<-a实数的大小“PK”
小结与作业
习得
感悟
放飞
感悟:
(1)今天收获了什么?
小结与作业
感悟:
(2)学习的方式有什么不同?
小结与作业
感悟:
(3)研究的范式是什么?
小结与作业
发现问题
提出问题
分析问题
解决问题
无限不循环的数是什么数?能否与数轴上的点有对应关系?
类比有理数,无理数与数轴上的点有对应关系
对数进行分类分类整理,发现一类数是无限不循环小数
数的扩充(实数)
实数与数轴上的点是一一对应的
有序实数对与直角坐标系中的点也是一一对应的
习得:
(1)巩固性作业,书本P86习题T1、2、7
(2)探索性作业
试探索 为什么不能用分数表示出来?
(3)拓展性作业
从网络上查找有关无理数性质的资料,打印出来与同学来交流.
小结与作业
放飞(课外阅读):
《九章算术》(全译插图本 全新修订版) 张苍
《几何原本》 欧几里得
《 实数十进表示》王昆扬
掌声送给聪明的同学们!
祝愿同学们学业有成!
数 的 扩 充
—— 13.3 实 数(第一课时)
关于数的分类整理(一)
问题1:说出下面各列数的名称
(整数)
(分数)
(有限小数和无限循环小数)
问题2:说出问题1中的三列数,它们共同的名称
(有理数)
它们均可化为分数
有理数的新认识
1.有理数的特征
注意:
(整数可以看成是小数部分是0的小数)
整数与有限小数的关系.
分数与有限小数或无限循环小数的关系.
(有限小数或无限循环小数可以看成是分数)
2.有理数的特征也可以这样理解:
见课本P82:任何一个有理数都可以写成有限小数或无限循环小数;反过来,任何有限小数或无限循环小数也都是有理数
可以写成: 形式的数叫有理数
关于数的分类整理(二)
问题1:观察下面各列数的特征
(1)
(2)
e是自然对数的底,e=2.718281828……
是圆周率,
它们都是无限不循环小数)
(相邻两个3之间的7的个数逐次加1)
(3)
(本学期我们学方根和立方根,当然还有4次方根、 5次方根、n次方根,而这些数中有一些是有理数,还有一些不是有理数,即它们不是有限数、也不是无限循环的小数,它们是无限不循环的小数,)
(我们学过的数中,有一些是构造出来的无限不循环的无限小数),这此无限不循环的小数究竟是什么数?叫什么数呢?
(我们学过的数中,有一些含 ,含e的无限不循环的无限小数)
数的扩充
上面观察到的那些数中,无限不循环小数,
数学家给这些数取名为叫
无理数.
不能写成:
形式的数叫无理数.
无理数另一种说法
实数的认识
(1)有理数(有限数或无限循环小数)
可以写成: 形式的数
(2)无理数(无限不循环的无限小数)
不能写成:
形式的数
有理数与无理数统称为实数
实数的研究
(1)实数仍然是具有性质符号的数,有正实数,负实数,还有一个0.
(2).实数的分类:
1.实数的性质符号
实数
正实数
0
负实数
负有理数
负无理数
正无理数
正有理数
实数
有理数
无理数
正分数
负分数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
自然数
实数也可这样来分类:
分数
整数
正整数
0
负整数
例1:把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
2.实数与数轴上的点的关系
(1)有理数与数轴上的点有对应关系
0
1
2
4
3
-1
-2
每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢?
实数的研究
0
1
2
4
3
-1
-2
π
我们将直径为1的圆上一点与数轴上原点重合,并沿数轴向右滚动,我们来观察结果:
(2)无理数与数轴上的点有对应关系
实数的研究
你能在数轴上找到表示 这样的无理数的点吗?
这个无理数就在数轴上找到了相应的点表示了.
π
问题3:
0
1
2
4
3
-1
-2
问题4:边长为1的正方形,对角线长为多少 你能在数轴上找到表示这个数的点吗?还能找到表示这个数的相反数的点吗?
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.无论是表示有理的点或是表示无理数的点都是表示实数的点
实数与数轴上的点是一一对应的.
(1)有理数与轴上的点有对应关系
(2)无理数也能用数轴上的点来表示其对应关系
归纳
3.平面直角坐标系中的点与有序实数对的关系
(1)由有理数组成的有序数对与平面直角坐标系中的点对应
关系 P(-2,3)、Q( 3 ,1/3)
(2)由无理数组成的有序
数对与平面直角坐标系中的点
对应关系
(3)由有理数、无理数组成的
有序数对与平面直角坐标系
中的点对应关系
有序实数对与平面直角坐标系
中的点是一 一对应的
O
x
y
归纳
无理数的自画像
我们无理数是实数中的一员,都是无限小数,并且是无限不循环小数,鉴定我们的方法不少,带根号的一定是我们无理数, 也就是说我们一定
带有根号,两个无理数之积不一定是无理数,但我们两个无理数之和一定是无理数,不能用分数表示出的就是我们无理数,否则可以用分数表示出来的就是我的好朋友有理数了.
以上说法你认为正确吗?
1.下列关于实数的说法正确是( )
(A) 无理数就是开方开不尽的数
(B)无理数是无限小数
(C)无理数包括正无理数、0、负无理数
(D)无理数都可以用数轴上的点来表示,无限小数都是 无理数
A
D
A
练一练
例2:比较下列各组实数的大小
(1)-3与-5;
(2)
(3)
(4)如图,点A、B表示实数a、b,试比较
a、-a、b、-b的大小.
-a
-b
0
a
b
B
A
解:b<-a
小结与作业
习得
感悟
放飞
感悟:
(1)今天收获了什么?
小结与作业
感悟:
(2)学习的方式有什么不同?
小结与作业
感悟:
(3)研究的范式是什么?
小结与作业
发现问题
提出问题
分析问题
解决问题
无限不循环的数是什么数?能否与数轴上的点有对应关系?
类比有理数,无理数与数轴上的点有对应关系
对数进行分类分类整理,发现一类数是无限不循环小数
数的扩充(实数)
实数与数轴上的点是一一对应的
有序实数对与直角坐标系中的点也是一一对应的
习得:
(1)巩固性作业,书本P86习题T1、2、7
(2)探索性作业
试探索 为什么不能用分数表示出来?
(3)拓展性作业
从网络上查找有关无理数性质的资料,打印出来与同学来交流.
小结与作业
放飞(课外阅读):
《九章算术》(全译插图本 全新修订版) 张苍
《几何原本》 欧几里得
《 实数十进表示》王昆扬
掌声送给聪明的同学们!
祝愿同学们学业有成!
