人教四年级数学下册-1 四则运算 课件(共104张PPT)
文档属性
| 名称 | 人教四年级数学下册-1 四则运算 课件(共104张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 14:01:24 | ||
图片预览









文档简介
四则运算
小学四年级 数学
+
?
×
÷
9+3=12
+
?
×
÷
9+3=12
+
?
×
÷
9+3=12
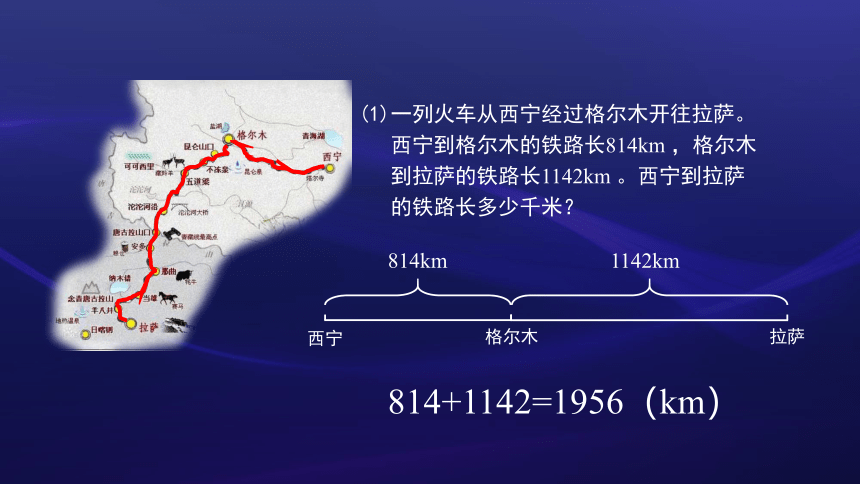
(1)一列火车从西宁经过格尔木开往拉萨。
西宁到格尔木的铁路长814km ,格尔木
到拉萨的铁路长1142km 。西宁到拉萨
的铁路长多少千米?
814km
1142km
814+1142=1956(km)
西宁
格尔木
拉萨
把两个数合并成一个数的运算,叫做加法。
天津战“疫”微型课
把两个数合并成一个数的运算,叫做加法。
把两个数合并成一个数的运算,叫做加法。
814+1142=1956(km)
加数
加数
和
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长814km。
格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。
西宁到格尔木的铁路长多少千米?
1956?814=1142(km)
1956?1142=814(km)
被减数
减数
差
被减数
减数
差
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长
814 km。格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长
1142km。西宁到格尔木的铁路长多少千米?
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木
的铁路长814km ,格尔木到拉萨的铁路长1142km 。西
宁到拉萨的铁路长多少千米?
814+1142=1956(km)
1956?814=1142(km)
1956?1142=814(km)
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长
814 km。格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长
1142km。西宁到格尔木的铁路长多少千米?
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木
的铁路长814km ,格尔木到拉萨的铁路长1142km 。西
宁到拉萨的铁路长多少千米?
814+1142=1956(km)
1956?814=1142(km)
1956?1142=814(km)
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长
814 km。格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长
1142km。西宁到格尔木的铁路长多少千米?
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木
的铁路长814km ,格尔木到拉萨的铁路长1142km 。西
宁到拉萨的铁路长多少千米?
814+1142=1956(km)
1956?814=1142(km)
1956?1142=814(km)
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长
814 km。格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长
1142km。西宁到格尔木的铁路长多少千米?
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木
的铁路长814km ,格尔木到拉萨的铁路长1142km 。西
宁到拉萨的铁路长多少千米?
814+1142=1956(km)
1956?814=1142(km)
1956?1142=814(km)
已知两个数的和与其中的一个加数,
求另一个加数的运算,叫做减法。
已知两个数的和与其中的一个加数,
求另一个加数的运算,叫做减法。
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分间的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分间的关系:
逆运算
加法
减法
根据加减法各部分间的关系,写出另外两个等式。
28+19=47
47-19=28
67-55=12
47-28=19
203+147=350
850-239=611
9 + 3 = 12
9 + 3 = 12
3
3
3
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
用加法算:3+3+3+3=12(枝)
用乘法算:3×4=12(枝)
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
用加法算:3+3+3+3=12(枝)
用乘法算:3×4=12(枝)
求几个相同加数的和的简便运算,叫做乘法。
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
用加法算:3+3+3+3=12(枝)
用乘法算:3×4=12(枝)
求几个相同加数的和的简便运算,叫做乘法。
因数
因数
积
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
12÷3 = 4(瓶)
12÷4 = 3(枝)
被除数
除数
商
被除数
除数
商
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
12÷3 = 4(瓶)
12÷4 = 3(枝)
被除数
除数
商
被除数
除数
商
已知两个因数的积与其中一个因数,求另一个
因数的运算,叫做除法。
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
12÷3 = 4(瓶)
12÷4 = 3(枝)
被除数
除数
商
被除数
除数
商
已知两个因数的积与其中一个因数,求另一个
因数的运算,叫做除法。
12÷3 = 4(瓶)
12÷4 = 3(枝)
3×4 = 12(枝)
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
12÷3 = 4(瓶)
12÷4 = 3(枝)
3×4 = 12(枝)
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
12÷3 = 4(瓶)
12÷4 = 3(枝)
3×4 = 12(枝)
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
积 = 因数×因数
积 = 因数×因数
积 = 因数×因数
因数 = 积÷另一个因数
积 = 因数×因数
因数 = 积÷另一个因数
乘法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
乘法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
乘法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
乘法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
除数 = 被除数÷商
被除数 = 商×除数
乘法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
除数 = 被除数÷商
被除数 = 商×除数
乘法各部分间的关系:
除法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
除数 = 被除数÷商
被除数 = 商×除数
乘法各部分间的关系:
除法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
除数 = 被除数÷商
被除数 = 商×除数
逆运算
乘法
除法
想一想:在有余数的除法里,被除数与商、除数和余数
之间有什么关系?
被除数 = 商× 除数 + 余数
?
每只猴分12个,
还余3个。
一共有多少个桃?
12×6+3=75(个)
口算抢答:
5+0 =
5?0 =
5×0 =
5÷0 =
口算抢答:
5+0 =5
5?0 =
5×0 =
5÷0 =
口算抢答:
5+0 =5
5?0 =5
5×0 =
5÷0 =
口算抢答:
5+0 =5
5?0 =5
5×0 =0
5÷0 =
口算抢答:
5+0 =5
5?0 =5
5×0 =0
5÷0 =
+
5÷0 =0
假如
0×0 =5
5÷0 =0
假如
0×0 ≠5
5÷0 =0
假如
0×0 ≠5
5÷0 =0
假如
+
0×0 ≠5
5÷0 =0
5÷0 =5
假如
假如
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 =5
假如
假如
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
假如
假如
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
假如
假如
+
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
0÷0 =?
假如
假如
+
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
0÷0 =?
任何数×0 =0
假如
假如
+
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
0÷0 =?
任何数×0 =0
0÷0 =任何数
假如
假如
+
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
0÷0 =?
任何数×0 =0
0÷0 =任何数
注意:0不能做除数。
假如
假如
+
+
已知 , 下面哪些算式是正确的?
正确的画“√”,错误的画“╳”
+
=
..
..
..
+
=
①
( ╳ )
+
=
÷
③
..
..
..
=
( √ )
×
②
( √ )
?
=
④
+
..
..
..
=
( ╳ )
加数
↑
加数
↑
和
↑
因数
↑
因数
↑
积
↑
已知 , 下面哪些算式是正确的?
正确的画“√”,错误的画“╳”
+
=
..
..
..
+
=
①
( ╳ )
+
=
÷
③
..
..
..
=
( √ )
×
②
( √ )
?
=
④
+
..
..
..
=
( ╳ )
加数
↑
加数
↑
和
↑
因数
↑
因数
↑
积
↑
已知 , 下面哪些算式是正确的?
正确的画“√”,错误的画“╳”
+
=
..
..
..
+
=
①
( ╳ )
+
=
÷
③
..
..
..
=
( √ )
×
②
( √ )
?
=
④
+
..
..
..
=
( ╳ )
加数
↑
加数
↑
和
↑
因数
↑
因数
↑
积
↑
已知 , 下面哪些算式是正确的?
正确的画“√”,错误的画“╳”
+
=
..
..
..
+
=
①
( ╳ )
+
=
÷
③
..
..
..
=
( √ )
×
②
( √ )
?
=
④
+
..
..
..
=
( ╳ )
加数
↑
加数
↑
和
↑
因数
↑
因数
↑
积
↑
已知 , 下面哪些算式是正确的?
正确的画“√”,错误的画“╳”
+
=
..
..
..
+
=
①
( ╳ )
+
=
÷
③
..
..
..
=
( √ )
×
②
( √ )
?
=
④
+
..
..
..
=
( ╳ )
加数
↑
加数
↑
和
↑
因数
↑
因数
↑
积
↑
+
?
×
÷
( )
计算96÷12 + 4×2 ,说一说运算的顺序。
96÷12 + 4×2
= 8 + 8
= 16
96÷(12 + 4)×2
96÷(12 + 4)×2
96÷(12 + 4)×2
96÷(12 + 4)×2
96÷(12 + 4)×2
=96÷16×2
96÷(12 + 4)×2
=96÷16×2
96÷(12 + 4)×2
=96÷16×2
=6×2
96÷(12 + 4)×2
=96÷16×2
=12
=6×2
请大家关注小括号哟
96÷[(12 + 4)×2]
96÷[(12 + 4)×2]
96÷[(12 + 4)×2]
96÷[(12 + 4)×2]
96÷[(12 + 4)×2]
=96÷[16×2]
96÷[(12 + 4)×2]
=96÷[16×2]
96÷[(12 + 4)×2]
=96÷[16×2]
=96÷32
96÷[(12 + 4)×2]
=96÷[16×2]
=96÷32
=3
要先算小括号里面的,
再算中括号里边的。
你知道吗?
小括号“( )”是公元17世纪由荷兰人吉拉特首先使用的。
中括号“[ ]”是公元17世纪英国数学家瓦里士最先使用的。
在以后的学习中,还会用到大括号“{ }”,又称为花括号。
大括号是法国数学家韦达在1593年首先使用的。
{ }
一看:运算顺序
小结:
二算:准确计算
三查:检查验算
同学们再见!
按照顺序计算,并填写下面的□,然后列出综合算式。
128
147
25
128
128
147
128
+
÷
×
73
438
920
34
128
147
128
÷
+
×
把下面每组用图形表示的算式改写成一个综合算式。
(1)
+
?
=
=
=
×
(2)
?
=
=
=
×
÷
把下面每组用图形表示的算式改写成一个综合算式。
(1)
+
?
=
=
=
×
(2)
?
=
=
=
×
÷
×
( )
( )
+
?
=
把下面每组用图形表示的算式改写成一个综合算式。
(1)
+
?
=
=
=
×
(2)
?
=
=
=
×
÷
×
( )
( )
+
?
=
×
÷
?
=
这节课我们讲解的是《四则运算》单元的知识,希望同学们理解掌握,融会贯通后,选做书上的习题。老师还要提醒同学们,计算过程中要仔细呦。先要判断运算顺序、还要计算准确、并且养成检查和验算的好习惯。
小结:
小学四年级 数学
+
?
×
÷
9+3=12
+
?
×
÷
9+3=12
+
?
×
÷
9+3=12
(1)一列火车从西宁经过格尔木开往拉萨。
西宁到格尔木的铁路长814km ,格尔木
到拉萨的铁路长1142km 。西宁到拉萨
的铁路长多少千米?
814km
1142km
814+1142=1956(km)
西宁
格尔木
拉萨
把两个数合并成一个数的运算,叫做加法。
天津战“疫”微型课
把两个数合并成一个数的运算,叫做加法。
把两个数合并成一个数的运算,叫做加法。
814+1142=1956(km)
加数
加数
和
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长814km。
格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。
西宁到格尔木的铁路长多少千米?
1956?814=1142(km)
1956?1142=814(km)
被减数
减数
差
被减数
减数
差
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长
814 km。格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长
1142km。西宁到格尔木的铁路长多少千米?
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木
的铁路长814km ,格尔木到拉萨的铁路长1142km 。西
宁到拉萨的铁路长多少千米?
814+1142=1956(km)
1956?814=1142(km)
1956?1142=814(km)
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长
814 km。格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长
1142km。西宁到格尔木的铁路长多少千米?
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木
的铁路长814km ,格尔木到拉萨的铁路长1142km 。西
宁到拉萨的铁路长多少千米?
814+1142=1956(km)
1956?814=1142(km)
1956?1142=814(km)
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长
814 km。格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长
1142km。西宁到格尔木的铁路长多少千米?
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木
的铁路长814km ,格尔木到拉萨的铁路长1142km 。西
宁到拉萨的铁路长多少千米?
814+1142=1956(km)
1956?814=1142(km)
1956?1142=814(km)
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长
814 km。格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长
1142km。西宁到格尔木的铁路长多少千米?
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木
的铁路长814km ,格尔木到拉萨的铁路长1142km 。西
宁到拉萨的铁路长多少千米?
814+1142=1956(km)
1956?814=1142(km)
1956?1142=814(km)
已知两个数的和与其中的一个加数,
求另一个加数的运算,叫做减法。
已知两个数的和与其中的一个加数,
求另一个加数的运算,叫做减法。
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分间的关系:
逆运算
和 = 加数 + 加数
加数 = 和 ? 另一个加数
差 = 被减数 ? 减数
减数 = 被减数 ? 差
被减数 = 减数 + 差
加法各部分间的关系:
减法各部分间的关系:
逆运算
加法
减法
根据加减法各部分间的关系,写出另外两个等式。
28+19=47
47-19=28
67-55=12
47-28=19
203+147=350
850-239=611
9 + 3 = 12
9 + 3 = 12
3
3
3
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
用加法算:3+3+3+3=12(枝)
用乘法算:3×4=12(枝)
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
用加法算:3+3+3+3=12(枝)
用乘法算:3×4=12(枝)
求几个相同加数的和的简便运算,叫做乘法。
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
用加法算:3+3+3+3=12(枝)
用乘法算:3×4=12(枝)
求几个相同加数的和的简便运算,叫做乘法。
因数
因数
积
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
12÷3 = 4(瓶)
12÷4 = 3(枝)
被除数
除数
商
被除数
除数
商
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
12÷3 = 4(瓶)
12÷4 = 3(枝)
被除数
除数
商
被除数
除数
商
已知两个因数的积与其中一个因数,求另一个
因数的运算,叫做除法。
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
12÷3 = 4(瓶)
12÷4 = 3(枝)
被除数
除数
商
被除数
除数
商
已知两个因数的积与其中一个因数,求另一个
因数的运算,叫做除法。
12÷3 = 4(瓶)
12÷4 = 3(枝)
3×4 = 12(枝)
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
12÷3 = 4(瓶)
12÷4 = 3(枝)
3×4 = 12(枝)
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
12÷3 = 4(瓶)
12÷4 = 3(枝)
3×4 = 12(枝)
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
积 = 因数×因数
积 = 因数×因数
积 = 因数×因数
因数 = 积÷另一个因数
积 = 因数×因数
因数 = 积÷另一个因数
乘法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
乘法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
乘法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
乘法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
除数 = 被除数÷商
被除数 = 商×除数
乘法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
除数 = 被除数÷商
被除数 = 商×除数
乘法各部分间的关系:
除法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
除数 = 被除数÷商
被除数 = 商×除数
乘法各部分间的关系:
除法各部分间的关系:
积 = 因数×因数
因数 = 积÷另一个因数
商 = 被除数÷除数
除数 = 被除数÷商
被除数 = 商×除数
逆运算
乘法
除法
想一想:在有余数的除法里,被除数与商、除数和余数
之间有什么关系?
被除数 = 商× 除数 + 余数
?
每只猴分12个,
还余3个。
一共有多少个桃?
12×6+3=75(个)
口算抢答:
5+0 =
5?0 =
5×0 =
5÷0 =
口算抢答:
5+0 =5
5?0 =
5×0 =
5÷0 =
口算抢答:
5+0 =5
5?0 =5
5×0 =
5÷0 =
口算抢答:
5+0 =5
5?0 =5
5×0 =0
5÷0 =
口算抢答:
5+0 =5
5?0 =5
5×0 =0
5÷0 =
+
5÷0 =0
假如
0×0 =5
5÷0 =0
假如
0×0 ≠5
5÷0 =0
假如
0×0 ≠5
5÷0 =0
假如
+
0×0 ≠5
5÷0 =0
5÷0 =5
假如
假如
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 =5
假如
假如
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
假如
假如
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
假如
假如
+
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
0÷0 =?
假如
假如
+
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
0÷0 =?
任何数×0 =0
假如
假如
+
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
0÷0 =?
任何数×0 =0
0÷0 =任何数
假如
假如
+
+
0×0 ≠5
5÷0 =0
5÷0 =5
0×5 ≠ 5
0÷0 =?
任何数×0 =0
0÷0 =任何数
注意:0不能做除数。
假如
假如
+
+
已知 , 下面哪些算式是正确的?
正确的画“√”,错误的画“╳”
+
=
..
..
..
+
=
①
( ╳ )
+
=
÷
③
..
..
..
=
( √ )
×
②
( √ )
?
=
④
+
..
..
..
=
( ╳ )
加数
↑
加数
↑
和
↑
因数
↑
因数
↑
积
↑
已知 , 下面哪些算式是正确的?
正确的画“√”,错误的画“╳”
+
=
..
..
..
+
=
①
( ╳ )
+
=
÷
③
..
..
..
=
( √ )
×
②
( √ )
?
=
④
+
..
..
..
=
( ╳ )
加数
↑
加数
↑
和
↑
因数
↑
因数
↑
积
↑
已知 , 下面哪些算式是正确的?
正确的画“√”,错误的画“╳”
+
=
..
..
..
+
=
①
( ╳ )
+
=
÷
③
..
..
..
=
( √ )
×
②
( √ )
?
=
④
+
..
..
..
=
( ╳ )
加数
↑
加数
↑
和
↑
因数
↑
因数
↑
积
↑
已知 , 下面哪些算式是正确的?
正确的画“√”,错误的画“╳”
+
=
..
..
..
+
=
①
( ╳ )
+
=
÷
③
..
..
..
=
( √ )
×
②
( √ )
?
=
④
+
..
..
..
=
( ╳ )
加数
↑
加数
↑
和
↑
因数
↑
因数
↑
积
↑
已知 , 下面哪些算式是正确的?
正确的画“√”,错误的画“╳”
+
=
..
..
..
+
=
①
( ╳ )
+
=
÷
③
..
..
..
=
( √ )
×
②
( √ )
?
=
④
+
..
..
..
=
( ╳ )
加数
↑
加数
↑
和
↑
因数
↑
因数
↑
积
↑
+
?
×
÷
( )
计算96÷12 + 4×2 ,说一说运算的顺序。
96÷12 + 4×2
= 8 + 8
= 16
96÷(12 + 4)×2
96÷(12 + 4)×2
96÷(12 + 4)×2
96÷(12 + 4)×2
96÷(12 + 4)×2
=96÷16×2
96÷(12 + 4)×2
=96÷16×2
96÷(12 + 4)×2
=96÷16×2
=6×2
96÷(12 + 4)×2
=96÷16×2
=12
=6×2
请大家关注小括号哟
96÷[(12 + 4)×2]
96÷[(12 + 4)×2]
96÷[(12 + 4)×2]
96÷[(12 + 4)×2]
96÷[(12 + 4)×2]
=96÷[16×2]
96÷[(12 + 4)×2]
=96÷[16×2]
96÷[(12 + 4)×2]
=96÷[16×2]
=96÷32
96÷[(12 + 4)×2]
=96÷[16×2]
=96÷32
=3
要先算小括号里面的,
再算中括号里边的。
你知道吗?
小括号“( )”是公元17世纪由荷兰人吉拉特首先使用的。
中括号“[ ]”是公元17世纪英国数学家瓦里士最先使用的。
在以后的学习中,还会用到大括号“{ }”,又称为花括号。
大括号是法国数学家韦达在1593年首先使用的。
{ }
一看:运算顺序
小结:
二算:准确计算
三查:检查验算
同学们再见!
按照顺序计算,并填写下面的□,然后列出综合算式。
128
147
25
128
128
147
128
+
÷
×
73
438
920
34
128
147
128
÷
+
×
把下面每组用图形表示的算式改写成一个综合算式。
(1)
+
?
=
=
=
×
(2)
?
=
=
=
×
÷
把下面每组用图形表示的算式改写成一个综合算式。
(1)
+
?
=
=
=
×
(2)
?
=
=
=
×
÷
×
( )
( )
+
?
=
把下面每组用图形表示的算式改写成一个综合算式。
(1)
+
?
=
=
=
×
(2)
?
=
=
=
×
÷
×
( )
( )
+
?
=
×
÷
?
=
这节课我们讲解的是《四则运算》单元的知识,希望同学们理解掌握,融会贯通后,选做书上的习题。老师还要提醒同学们,计算过程中要仔细呦。先要判断运算顺序、还要计算准确、并且养成检查和验算的好习惯。
小结:
