5.4 平移(2)
图片预览





文档简介
(共21张PPT)
第五章 相交线与平行线
5.4 平移(2)
重庆市开县西街中学 罗堂喜
⑴什么叫做平移?
⑵图形的平移变换具有哪些特征?
⑶图形平移的性质?平移方向必须是水平的吗?
复习回顾
平移作图---线段平移
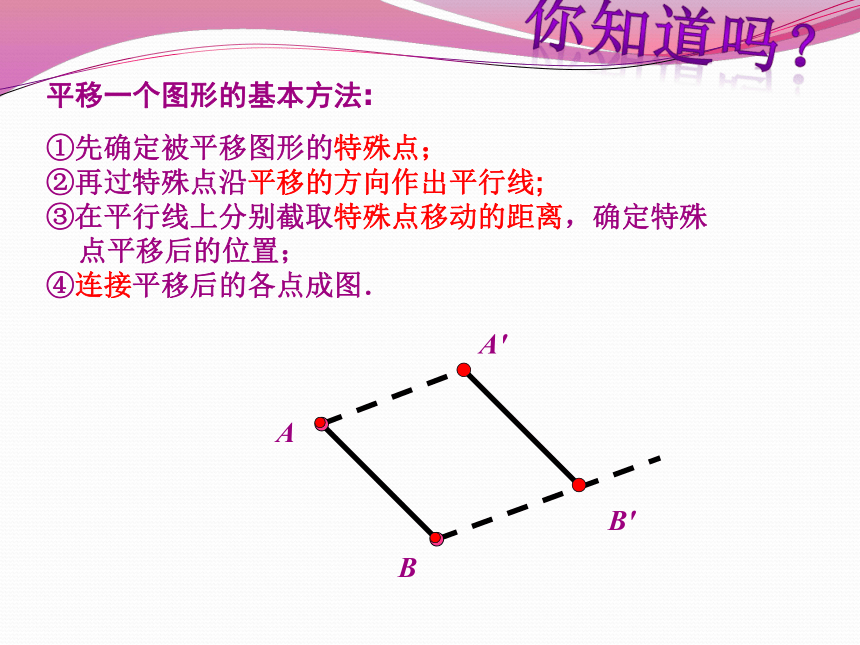
如图,已知线段AB,平移线段AB,使端点A 平移到A',你能作出线段AB平移后的图形A'B′吗?
⑷根据平移的性质特征如何确定B点移动后的位置B′点?
⑴要想平移整条线段,需要把握上哪些关键的点?
⑵平移的方向是什么?
⑶平移的距离是谁的长度?
①先确定被平移图形的特殊点;
②再过特殊点沿平移的方向作出平行线;
③在平行线上分别截取特殊点移动的距离,确定特殊点平移后的位置;
④连接平移后的各点成图.
B
A
A'
B'
平移一个图形的基本方法:
C
A
B
A'
例题:
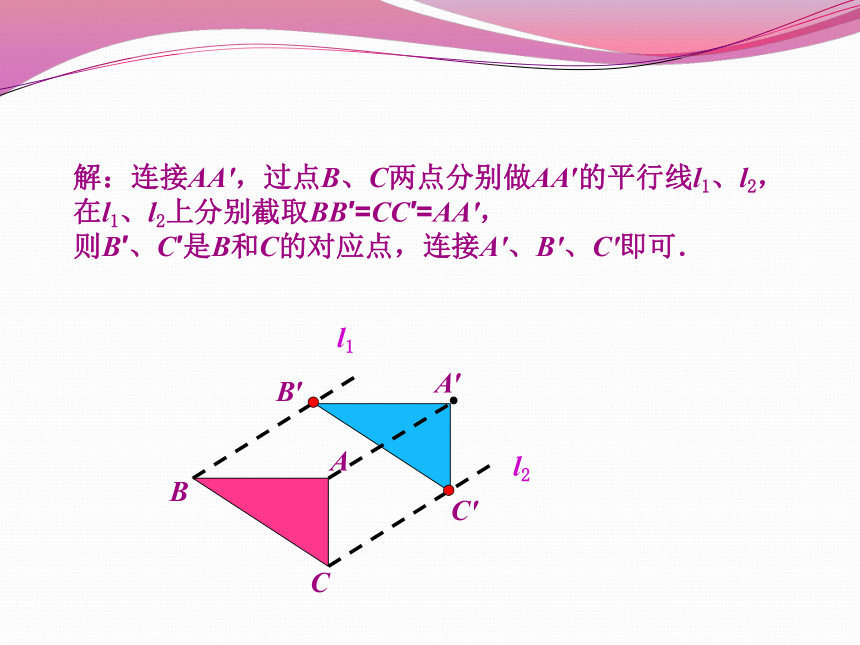
如图,平移三角形ABC,使点A移动到点A’,画出平移后的三角形A’B’C’.
解:连接AA′,过点B、C两点分别做AA′的平行线l1、l2,
在l1、l2上分别截取BB′=CC′=AA′,
则B′、C′是B和C的对应点,连接A′、B′、C′即可.
C
A
B
A′
C′
B′
l1
l2
A
D
B
C
C
A
B
D
例:把长方形ABCD(如图)沿箭头所指的方向平移,使点C落在点C’。求经这一平移变换后所得的像。
点B平移的方向和距离?
要画长方形需确定点的位置。
共同完成作图步骤、下结论
平移时作关键点的的像是图形平移变换作图的基本方法
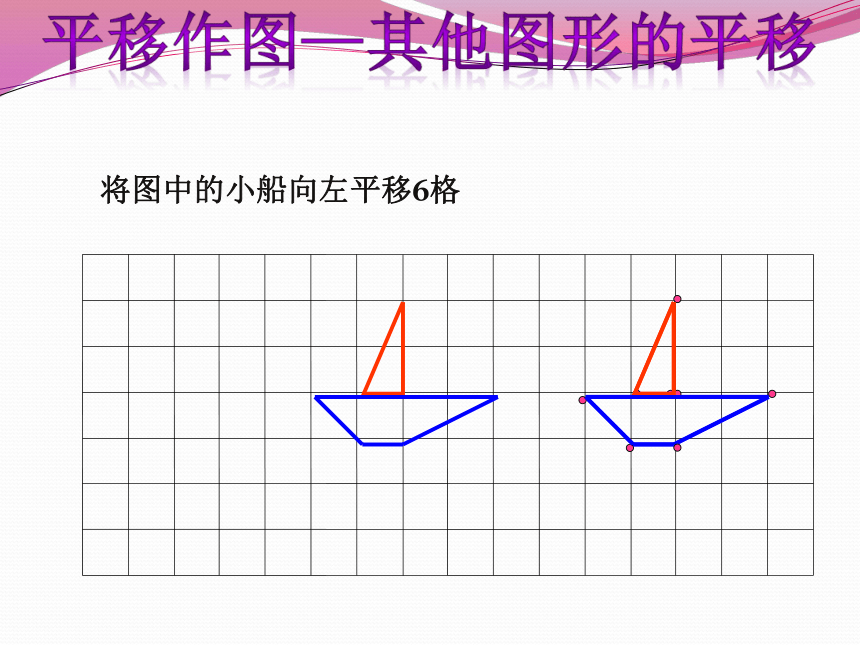
将图中的小船向左平移6格
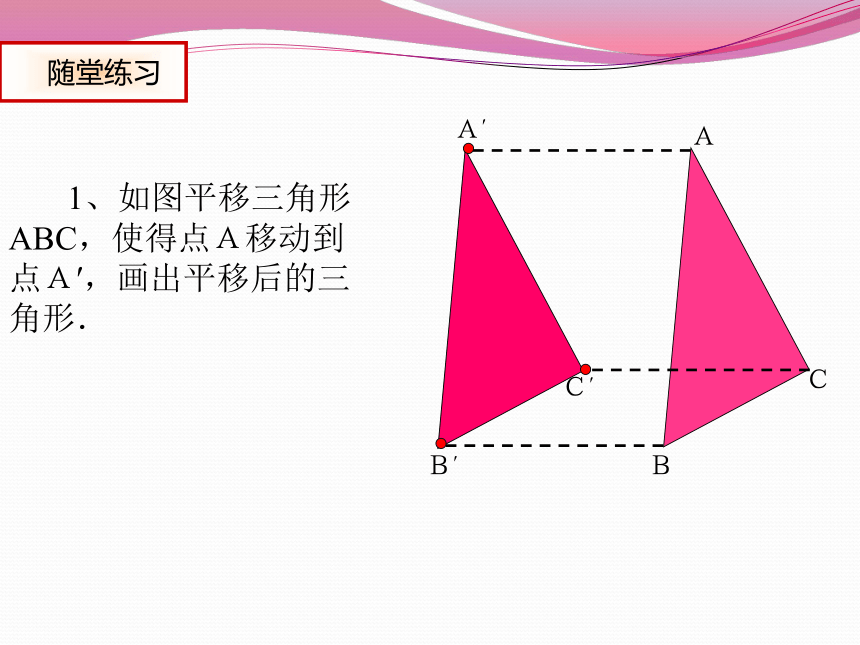
1、如图平移三角形ABC,使得点A移动到点A′,画出平移后的三角形.
A′
A
B
C
C′
B′
随堂练习
X
Y
A
B
C
D
E
F
2、△ABC沿着射线XY的方向平移一定距离后成为△DEF。画出图形,并找出图中平行且相等的三条线段。
解:如图:
图中AD∥BE∥CF
并且AD=BE=CF
随堂练习
1. 下面两幅图案是由什么“基本图案”通过平移得到的?
当堂检测
3.如图,已知长方形的是2cm,
宽是1cm,求阴影部分的面积.
2. 如图,四边形EFGH是由四
边形ABCD经过平移后得到的,请指出图中的对应点、对应线段和对应角,并说明是怎样平移得到的.
当堂检测
如图1是10枚硬币的三角形,现在只许你移动3枚硬币,使图1中变成图2的倒三角形,请同桌为一组,合作交流,动手移移看。
图1
图2
当堂检测
2、如图,在一块长方形的草地上,有人设计了不同的小路,但任何地方的宽度一样,都是a,问种花草的部分面积哪个大?为什么?
a
a
a
b
b
b
c
c
c
拓展探究
练习反馈
1.如图,经过平移,四边形ABCD的顶点A移动到点A′,作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
练习反馈
2.如图所示,点A, B, C, D在同一条直线上 , AB=CD, ∠D=∠ECA, EC=FD.试说明AE=BF.
A
B
C
D
F
E
解:因为AB=CD,∠D=∠ECA,EC=FD,所以△AEC 沿AC方向平移了AB长得到△ BFD,根据平移的性质得到AE=BF.
1.平移的性质是对应点的连结线段 且 .
2.平移的作图方法:⑴先找出图形上的关键点;⑵过这些点沿指定的 平移,使平移 等于已知距离;⑶依次作出各个 点,连结平移后的点得到平移图形.
3.将下图的平行四边形沿所给的箭头方向平移3厘米.
自我完善
平行
相等
方向
距离
对应
A
B
C
D
A′
B′
C′
D′
4.如图,四边形ABCD中,AD∥BC,且AD<BC,△ABC平移到△DEF的位置.⑴指出平移的方向和平移的距离;⑵试说明AD+BC=BF.
A
D
B
E
C
F
(1)沿BC方向移动,平移的距离是AD长或BE长或CF长.
(2)因为△DEF 是由△ABC平移AD长得到,由平移的性质得BE=AD=CF,所以BF=BC+CF=BC+AD.
总结归纳
1、平移一个图形的基本方法
①先确定被平移图形的特殊点;
②再过特殊点沿平移的方向作出平行线;
③在平行线上分别截取特殊点移动的距离,确定特殊点平移后的位置;
④连接平移后的各点成图.
2、图形的平移
点的平移
实质上
图形的运动
点的运动
实质上
延伸:
3、平移的特点
方向
距离
教科书:第31页习题5.4第5、6题,
第37页复习题5第11题.
备选题:
将下图中的大写英文字母“N”沿指定方向平移0.5厘米,并装饰成立体图形.
作业布置
第五章 相交线与平行线
5.4 平移(2)
重庆市开县西街中学 罗堂喜
⑴什么叫做平移?
⑵图形的平移变换具有哪些特征?
⑶图形平移的性质?平移方向必须是水平的吗?
复习回顾
平移作图---线段平移
如图,已知线段AB,平移线段AB,使端点A 平移到A',你能作出线段AB平移后的图形A'B′吗?
⑷根据平移的性质特征如何确定B点移动后的位置B′点?
⑴要想平移整条线段,需要把握上哪些关键的点?
⑵平移的方向是什么?
⑶平移的距离是谁的长度?
①先确定被平移图形的特殊点;
②再过特殊点沿平移的方向作出平行线;
③在平行线上分别截取特殊点移动的距离,确定特殊点平移后的位置;
④连接平移后的各点成图.
B
A
A'
B'
平移一个图形的基本方法:
C
A
B
A'
例题:
如图,平移三角形ABC,使点A移动到点A’,画出平移后的三角形A’B’C’.
解:连接AA′,过点B、C两点分别做AA′的平行线l1、l2,
在l1、l2上分别截取BB′=CC′=AA′,
则B′、C′是B和C的对应点,连接A′、B′、C′即可.
C
A
B
A′
C′
B′
l1
l2
A
D
B
C
C
A
B
D
例:把长方形ABCD(如图)沿箭头所指的方向平移,使点C落在点C’。求经这一平移变换后所得的像。
点B平移的方向和距离?
要画长方形需确定点的位置。
共同完成作图步骤、下结论
平移时作关键点的的像是图形平移变换作图的基本方法
将图中的小船向左平移6格
1、如图平移三角形ABC,使得点A移动到点A′,画出平移后的三角形.
A′
A
B
C
C′
B′
随堂练习
X
Y
A
B
C
D
E
F
2、△ABC沿着射线XY的方向平移一定距离后成为△DEF。画出图形,并找出图中平行且相等的三条线段。
解:如图:
图中AD∥BE∥CF
并且AD=BE=CF
随堂练习
1. 下面两幅图案是由什么“基本图案”通过平移得到的?
当堂检测
3.如图,已知长方形的是2cm,
宽是1cm,求阴影部分的面积.
2. 如图,四边形EFGH是由四
边形ABCD经过平移后得到的,请指出图中的对应点、对应线段和对应角,并说明是怎样平移得到的.
当堂检测
如图1是10枚硬币的三角形,现在只许你移动3枚硬币,使图1中变成图2的倒三角形,请同桌为一组,合作交流,动手移移看。
图1
图2
当堂检测
2、如图,在一块长方形的草地上,有人设计了不同的小路,但任何地方的宽度一样,都是a,问种花草的部分面积哪个大?为什么?
a
a
a
b
b
b
c
c
c
拓展探究
练习反馈
1.如图,经过平移,四边形ABCD的顶点A移动到点A′,作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
练习反馈
2.如图所示,点A, B, C, D在同一条直线上 , AB=CD, ∠D=∠ECA, EC=FD.试说明AE=BF.
A
B
C
D
F
E
解:因为AB=CD,∠D=∠ECA,EC=FD,所以△AEC 沿AC方向平移了AB长得到△ BFD,根据平移的性质得到AE=BF.
1.平移的性质是对应点的连结线段 且 .
2.平移的作图方法:⑴先找出图形上的关键点;⑵过这些点沿指定的 平移,使平移 等于已知距离;⑶依次作出各个 点,连结平移后的点得到平移图形.
3.将下图的平行四边形沿所给的箭头方向平移3厘米.
自我完善
平行
相等
方向
距离
对应
A
B
C
D
A′
B′
C′
D′
4.如图,四边形ABCD中,AD∥BC,且AD<BC,△ABC平移到△DEF的位置.⑴指出平移的方向和平移的距离;⑵试说明AD+BC=BF.
A
D
B
E
C
F
(1)沿BC方向移动,平移的距离是AD长或BE长或CF长.
(2)因为△DEF 是由△ABC平移AD长得到,由平移的性质得BE=AD=CF,所以BF=BC+CF=BC+AD.
总结归纳
1、平移一个图形的基本方法
①先确定被平移图形的特殊点;
②再过特殊点沿平移的方向作出平行线;
③在平行线上分别截取特殊点移动的距离,确定特殊点平移后的位置;
④连接平移后的各点成图.
2、图形的平移
点的平移
实质上
图形的运动
点的运动
实质上
延伸:
3、平移的特点
方向
距离
教科书:第31页习题5.4第5、6题,
第37页复习题5第11题.
备选题:
将下图中的大写英文字母“N”沿指定方向平移0.5厘米,并装饰成立体图形.
作业布置
