18.1.1平行四边形的性质-2020-2021学年人教版八年级数学下册课件(20张)
文档属性
| 名称 | 18.1.1平行四边形的性质-2020-2021学年人教版八年级数学下册课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
18.1.1
平行四边形的性质
平行四边形的定义
A
B
C
D
定义:两组对边分别平行的四边形是平行四边形
符号:平行四边形用“
”表示。
如图:平行四边形ABCD记作“
ABCD”
几何语言:
如图,∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
平行四边形的其它概念
对角线:平行四边形不相邻的两个顶点连成的线段叫它的对角线
如图,AC,BD是平行四边形ABCD的两条对角线
A
B
C
D
对边:相对的边称为对边
邻边:相邻的边称为邻边
如图,AB和CD是平行四边形ABCD的一组对边,AB和BC是一组邻边
对角:相对的角称为对角
邻角:相邻的角称为邻角
如图,∠ABC和∠ADC是平行四边形ABCD的一组对角,
∠ABC和∠BCD是一组邻角
平行四边形的性质1
A
B
C
D
平行四边形的两组对边分别平行
几何语言:
如图,∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的边之间还有什么关系?它的角之间有什么关系?度量一下,和你的猜想一致吗?
探究
A
B
C
D
猜想:平行四边形的对边相等;
平行四边形的对角相等。
A
B
C
D
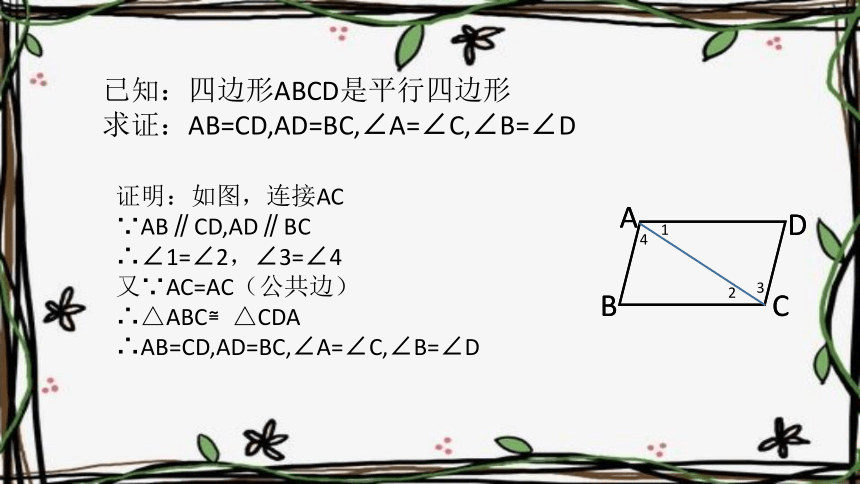
已知:四边形ABCD是平行四边形
求证:AB=CD,AD=BC,∠A=∠C,∠B=∠D
A
B
C
D
1
4
2
3
证明:如图,连接AC
∵AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
又∵AC=AC(公共边)
∴△ABC≌△CDA
∴AB=CD,AD=BC,∠A=∠C,∠B=∠D
性质2:平行四边形的对边相等;
性质3:平行四边形的对角相等,邻角互补。
A
B
C
D
几何语言:
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠A=∠C,∠B=∠D
平行四边形的两组对边分别平行
平行四边形的对边相等
平行四边形的对边平行且相等
∥
=
读作:平行且相等
A
B
C
D
AB
CD,读作:AB平行等于CD
∥
=
1.如图,将
ABCD的一边BC延长至点E。若∠A=110°,则∠1等于(
)
A.110°
B.35°
C.70°
D.55°
C
A
B
C
D
2.如图,在
ABCD中,AB=3,BC=4,则平行四边形ABCD的周长是
14
3、如图,在平行四边形ABCD中,DE⊥AB,BF⊥CD,
垂足分别是E,F.求证:AE=CF.
如图,a∥b,c∥d,c,d与a,b分别相交于A,B,C,D四点,由平行四边形的概念与性质可知,四边形ABCD是平行四边形,AB=CD,
也就是说,两条平行线之间的任何两条平行线段都相等。
两条平行线之间的距离的概念
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如图,a∥b,A是a上的任意点,AB⊥b,B是垂足,
线段AB的长就是a,b之间的距离.
探究:如图,在
ABCD中,连接AC,BD,并设它们相交于点O,
OA与OC,OB与OD有什么关系?
OA=OC
OB=OD
性质4:平行四边形的对角线互相平分
几何语言:
∵四边形ABCD是平行四边形
∴OA=OC,OD=OB
4、如图,在平行四边形ABCD中,点E在边AD上,以C为圆心,
AE长为半径画弧,交边BC于点F,连接BE,DF.求证:△ABE≌△CDF
5、如图,已知四边形ABCD是平行四边,点E,B,D,F在同一直线上.
且BE=DF.求证:AE=CF
6.如图,
ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长
可能是(
)
A.10
B.8
C.7
D.6
D
7.如图,
ABCD的对角线AC,BD交于点O,经过点O的直线交AB于点E,
交CD于点F.求证:OE=OF
18.1.1
平行四边形的性质
平行四边形的定义
A
B
C
D
定义:两组对边分别平行的四边形是平行四边形
符号:平行四边形用“
”表示。
如图:平行四边形ABCD记作“
ABCD”
几何语言:
如图,∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
平行四边形的其它概念
对角线:平行四边形不相邻的两个顶点连成的线段叫它的对角线
如图,AC,BD是平行四边形ABCD的两条对角线
A
B
C
D
对边:相对的边称为对边
邻边:相邻的边称为邻边
如图,AB和CD是平行四边形ABCD的一组对边,AB和BC是一组邻边
对角:相对的角称为对角
邻角:相邻的角称为邻角
如图,∠ABC和∠ADC是平行四边形ABCD的一组对角,
∠ABC和∠BCD是一组邻角
平行四边形的性质1
A
B
C
D
平行四边形的两组对边分别平行
几何语言:
如图,∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的边之间还有什么关系?它的角之间有什么关系?度量一下,和你的猜想一致吗?
探究
A
B
C
D
猜想:平行四边形的对边相等;
平行四边形的对角相等。
A
B
C
D
已知:四边形ABCD是平行四边形
求证:AB=CD,AD=BC,∠A=∠C,∠B=∠D
A
B
C
D
1
4
2
3
证明:如图,连接AC
∵AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
又∵AC=AC(公共边)
∴△ABC≌△CDA
∴AB=CD,AD=BC,∠A=∠C,∠B=∠D
性质2:平行四边形的对边相等;
性质3:平行四边形的对角相等,邻角互补。
A
B
C
D
几何语言:
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠A=∠C,∠B=∠D
平行四边形的两组对边分别平行
平行四边形的对边相等
平行四边形的对边平行且相等
∥
=
读作:平行且相等
A
B
C
D
AB
CD,读作:AB平行等于CD
∥
=
1.如图,将
ABCD的一边BC延长至点E。若∠A=110°,则∠1等于(
)
A.110°
B.35°
C.70°
D.55°
C
A
B
C
D
2.如图,在
ABCD中,AB=3,BC=4,则平行四边形ABCD的周长是
14
3、如图,在平行四边形ABCD中,DE⊥AB,BF⊥CD,
垂足分别是E,F.求证:AE=CF.
如图,a∥b,c∥d,c,d与a,b分别相交于A,B,C,D四点,由平行四边形的概念与性质可知,四边形ABCD是平行四边形,AB=CD,
也就是说,两条平行线之间的任何两条平行线段都相等。
两条平行线之间的距离的概念
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如图,a∥b,A是a上的任意点,AB⊥b,B是垂足,
线段AB的长就是a,b之间的距离.
探究:如图,在
ABCD中,连接AC,BD,并设它们相交于点O,
OA与OC,OB与OD有什么关系?
OA=OC
OB=OD
性质4:平行四边形的对角线互相平分
几何语言:
∵四边形ABCD是平行四边形
∴OA=OC,OD=OB
4、如图,在平行四边形ABCD中,点E在边AD上,以C为圆心,
AE长为半径画弧,交边BC于点F,连接BE,DF.求证:△ABE≌△CDF
5、如图,已知四边形ABCD是平行四边,点E,B,D,F在同一直线上.
且BE=DF.求证:AE=CF
6.如图,
ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长
可能是(
)
A.10
B.8
C.7
D.6
D
7.如图,
ABCD的对角线AC,BD交于点O,经过点O的直线交AB于点E,
交CD于点F.求证:OE=OF
