2020-2021学年 人教版八年级数学下册 第18章平行四边形 期中复习优生辅导训练(Word版 含答案)
文档属性
| 名称 | 2020-2021学年 人教版八年级数学下册 第18章平行四边形 期中复习优生辅导训练(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 313.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 00:00:00 | ||
图片预览


文档简介
2021年度人教版八年级数学下册《第18章平行四边形》期中复习优生辅导训练(附答案)
1.下列说法正确的是( )
A.对角线互相垂直的四边形是菱形
B.矩形的对角线互相垂直
C.一组对边平行的四边形是平行四边形
D.对角线相等的平行四边形是矩形
2.平行四边形一边长是10cm,那么它的两条对角线的长度可以是( )
A.8cm和6cm
B.8cm和8cm
C.8cm和12cm
D.8cm和16cm
3.如图,在?ABCD中,BE⊥AB交对角线AC于点E.若∠1=20°,则∠2的度数为( )
A.120°
B.100°
C.110°
D.90°
4.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24
B.24
C.12
D.12
5.如图,四边形ABCD中,以对角线AC为斜边作Rt△ACE,连接BE、DE,BE⊥DE,AC,BD互相平分.若2AB=BC=4,则BD的值为( )
A.2
B.
C.3
D.4
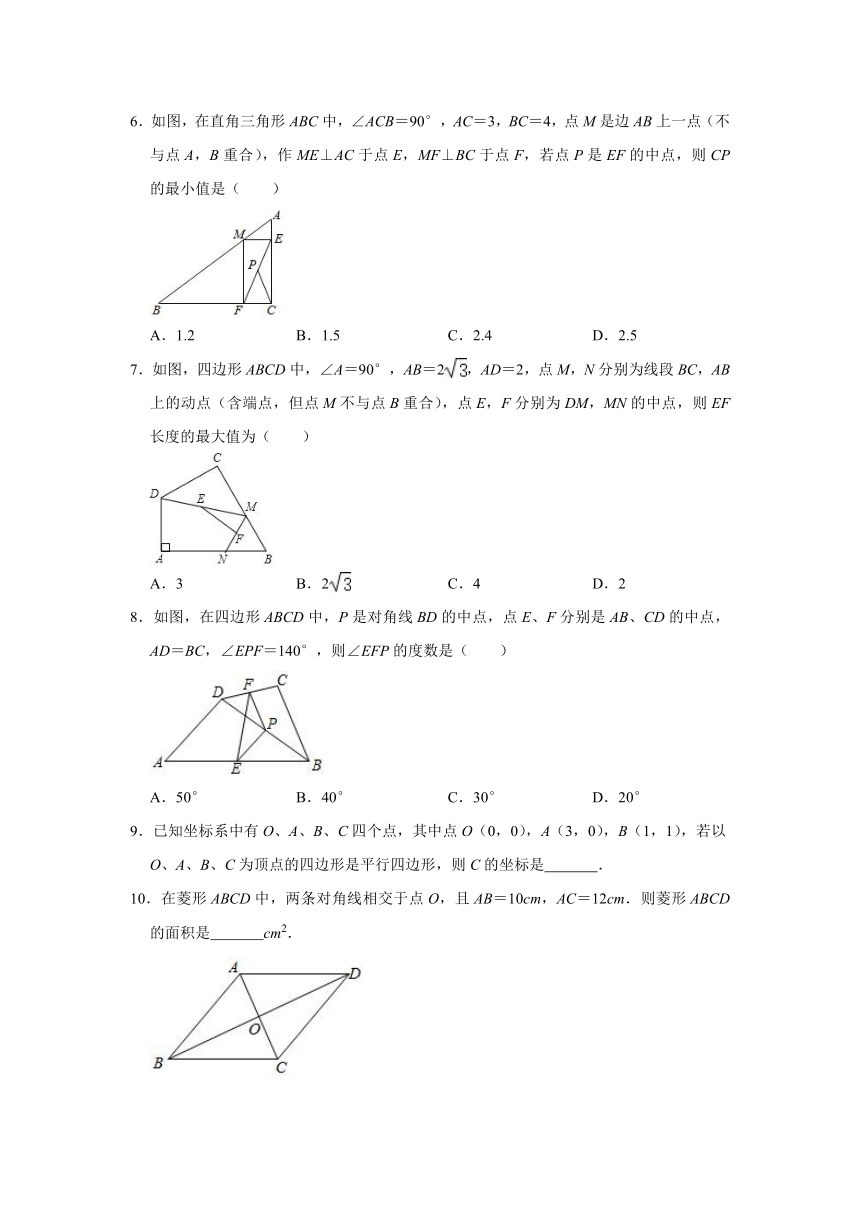
6.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2
B.1.5
C.2.4
D.2.5
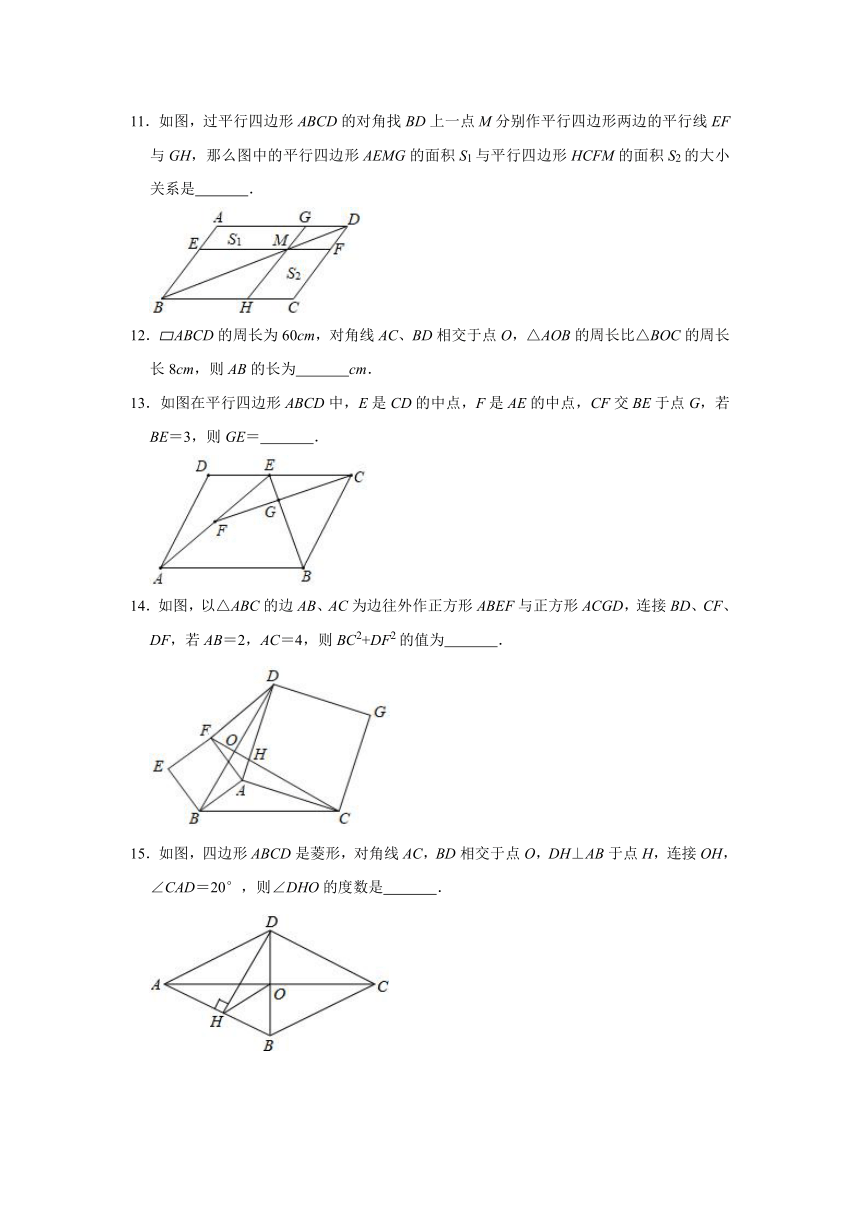
7.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3
B.2
C.4
D.2
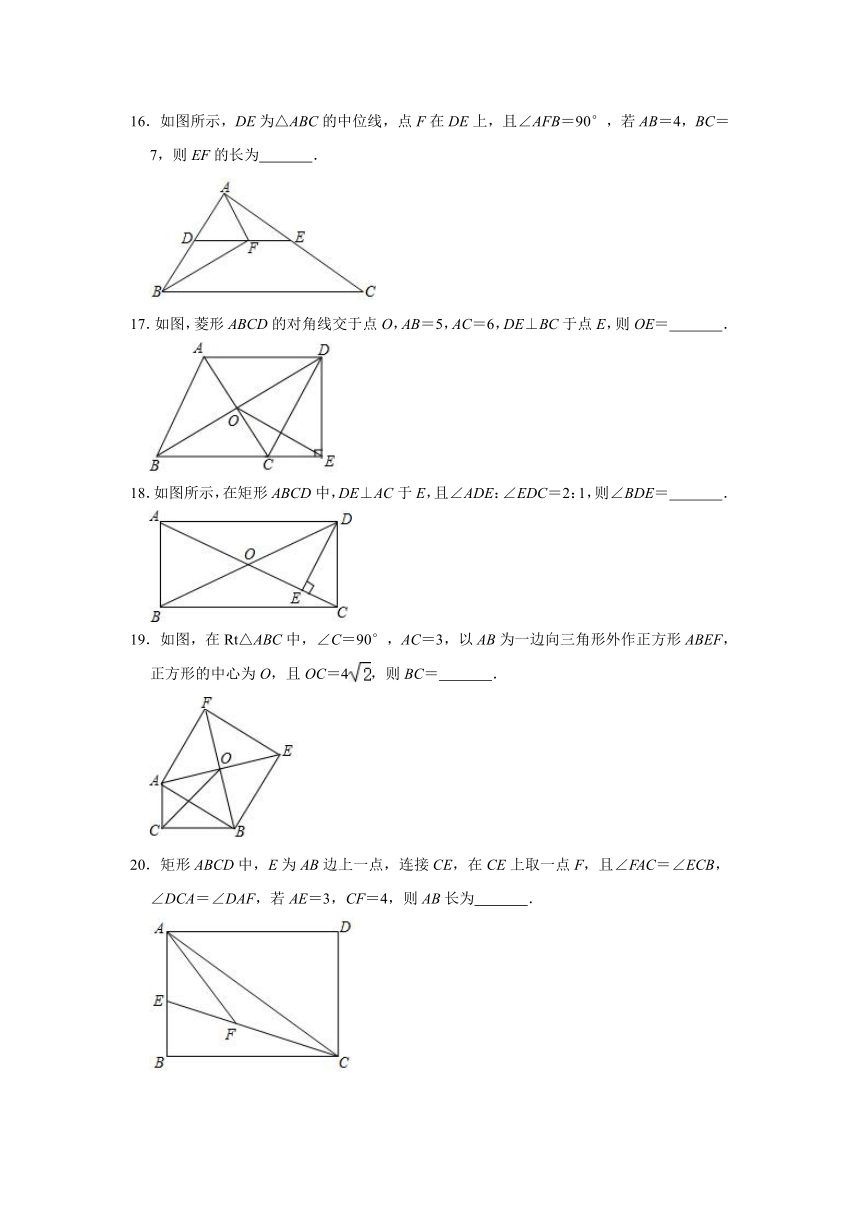
8.如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )
A.50°
B.40°
C.30°
D.20°
9.已知坐标系中有O、A、B、C四个点,其中点O(0,0),A(3,0),B(1,1),若以O、A、B、C为顶点的四边形是平行四边形,则C的坐标是
.
10.在菱形ABCD中,两条对角线相交于点O,且AB=10cm,AC=12cm.则菱形ABCD的面积是
cm2.
11.如图,过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是
.
12.?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,则AB的长为
cm.
13.如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=3,则GE=
.
14.如图,以△ABC的边AB、AC为边往外作正方形ABEF与正方形ACGD,连接BD、CF、DF,若AB=2,AC=4,则BC2+DF2的值为
.
15.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是
.
16.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=7,则EF的长为
.
17.如图,菱形ABCD的对角线交于点O,AB=5,AC=6,DE⊥BC于点E,则OE=
.
18.如图所示,在矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=2:1,则∠BDE=
.
19.如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,且OC=4,则BC=
.
20.矩形ABCD中,E为AB边上一点,连接CE,在CE上取一点F,且∠FAC=∠ECB,∠DCA=∠DAF,若AE=3,CF=4,则AB长为
.
21.如图,在四边形ABCD中,AC、BD交于点O,AE⊥BD,CF⊥BD,E、F分别为垂足,BE=DF,AF∥CE.
(1)试判断四边形AECF、四边形ABCD形状,并说明理由;
(2)如果AF=10,EF=8,BE=7,求BC.
22.如图,已知四边形ABCD是正方形,点E、F分别在AD、DC上,BE与AF相交于点G,且BE=AF.
(1)求证:△ABE≌△DAF;
(2)求证:BE⊥AF;
(3)如果正方形ABCD的边长为5,AE=2,点H为BF的中点,连接GH.求GH的长.
23.在正方形ABCD中,点P为射线BA上的一个动点(与点B不重合).当DP的垂直平分线交线段AC于点E时,猜想:∠PDE的度数是多少?当点P运动时,∠PDE的度数是否发生改变?
请你按①如图①,点P在AB上,②如图②,点P在BA延长线上,两种情况进行探究.
(1)完成图形,写出你的猜想;
(2)选择其中的一种情况给出证明.
24.如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,OE=2,求四边形ABCD的面积.
25.如图,在矩形ABCD中,点E、F为对角线AC上两点,且AF=CE.
(1)证明:四边形DEBF为平行四边形;
(2)若DE⊥AC,∠ADE=30°,AD=2,求平行四边形DEBF的面积.
26.图,点E、F分别在?ABCD的边AB、CD的延长线上,且BE=DF,连接AC、EF、AF、CE,AC与EF交于点O.
(1)求证:AC、EF互相平分;
(2)若EF平分∠AEC,判断四边形AECF的形状并证明.
27.如图,已知正方形ABCD的面积是8,连接AC、BD交于点O,CM平分∠ACD交BD于点M,MN⊥CM,交AB于点N,
(1)求∠BMN的度数;
(2)求BN的长.
28.如图,在四边形ABCD中,AD=BC,E、F分别是边DC、AB的中点,FE的延长线分别AD、BC的延长线交于点H、G,求证:∠AHF=∠BGF.
参考答案
1.解:A、∵对角线互相垂直平分的四边形是菱形,
∴选项A不符合题意;
B、∵矩形的对角线互相平分且相等,
∴选项B不符合题意;
C、∵两组对边分别平行的四边形是平行四边形,
∴选项C不符合题意;
D、∵对角线相等的平行四边形是矩形,
∴选项D符合题意;
故选:D.
2.解:A、取对角线的一半与已知边长,得4,3,10,不能构成三角形,舍去;
B、取对角线的一半与已知边长,得4,4,10,不能构成三角形,舍去;
C、取对角线的一半与已知边长,得4,6,10,不能构成三角形,舍去;
D、取对角线的一半与已知边长,得4,8,10,能构成三角形.
故选:D.
3.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠CAB=∠1=20°,
∵BE⊥AB,
∴∠ABE=90°,
∴∠2=∠EAB+∠EBA=20°+90°=110°.
故选:C.
4.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
故选:C.
5.解:连接OE,如图所示:
∵2AB=BC=4,
∴AB=2,
∵AC,BD互相平分,
∴OA=OC,OB=OD,四边形ABCD是平行四边形,
∵以AC为斜边作Rt△ACE,
∴OE=OA=OC=AC,
∵BE⊥DE,
∴OE=OB=OD=BD,
∴AC=BD,
∴四边形ABCD是矩形,
∴AD=BC=4,∠BAD=90°,
∴BD===2,
故选:A.
6.解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM===2.4,
∴CP=EF=CM=1.2,
故选:A.
7.解:连接DN、DB,
在Rt△DAB中,∠A=90°,AB=2,AD=2,
∴BD==4,
∵点E,F分别为DM,MN的中点,
∴EF=DN,
由题意得,当点N与点B重合是DN最大,最大值为4,
∴EF长度的最大值为2,
故选:D.
8.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠EFP=×(180°﹣∠EPF)=×(180°﹣140°)=20°,
故选:D.
9.解:如图所示:
分三种情况:①AB为对角线时,点C的坐标为(4,1);
②OB为对角线时,点C的坐标为(﹣2,1);
③OA为对角线时,点C的坐标为(2,﹣1);
综上所述,点C的坐标为(4,1)或(﹣2,1)或(2,﹣1),
故答案为:(4,1)或(﹣2,1)或(2,﹣1).
10.解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=AC=6cm,OB=OD,
∴OB===8(cm),
∴BD=2OB=16cm,
∴S菱形ABCD=AC?BD=×12×16=96(cm2).
故答案为:96.
11.解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故答案为:S1=S2.
12.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,OB=OD,
又平行四边形ABCD的周长为60cm,△AOB的周长比△BOC的周长长8cm,
∴,
两个方程相加,得AB=19(cm).
故答案为:19.
13.解:取BE的中点H,连接FH、CH,如图:
∵F是AE的中点,H是BE的中点,
∴FH是△ABE的中位线,
∴FH∥AB,FH=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E是CD的中点,
∴EC=CD,
∴FH∥EC,FH=EC,
∴四边形FHCE是平行四边形,
∴GE=GH=EH.
∵BE=3,H是BE的中点,
∴EH=,
∴GE=.
故答案为:.
14.解:如图所示,连接BF,CD,
∵四边形ABEF,四边形ACGD都是正方形,
∴AB=AF,AC=AD,∠BAF=∠CAD=90°,
∴∠BAD=∠FAC,
∴△BAD≌△FAC(SAS),
∴∠ACF=∠ADB,
又∵∠AHC=∠OHD,
∴∠CAH=∠DOH=90°,
∴CF⊥BD,
∴BC2=OB2+OC2,DF2=OD2+OF2,BF2=OB2+OF2,DC2=OD2+OC2,
∴BC2+DF2=OD2+OF2+OB2+OC2,
BF2+DC2=OD2+OF2+OB2+OC2,
即BC2+DF2=BF2+DC2,
又∵△ABF和△ACD都是等腰直角三角形,且AB=2,AC=4,
∴BF2+DC2=8+32=40,
∴BC2+DF2=40,
故答案为:40.
15.解:∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC,
∵DH⊥AB,
∴DH⊥CD,∠DHB=90°,
∴OH为Rt△DHB的斜边DB上的中线,
∴OH=OD=OB,
∴∠BDH=∠DHO,
∵DH⊥CD,
∴∠BDH+∠CDO=90°,
∵BD⊥AC,
∴∠CDO+∠DCO=90°,
∴∠BDH=∠DCO,
∴∠DHO=∠DCA,
∵四边形ABCD是菱形,
∴DA=DC,
∴∠CAD=∠DCA=20°,
∴∠DHO=20°,
故答案为:20°.
16.解:∵DE为△ABC的中位线,
∴DE=BC=3.5,
在Rt△AFB中,∠AFB=90°,D是AB的中点,
∴DF=AB=2,
∴EF=DE﹣DF=1.5,
故答案为:1.5.
17.解:∵四边形ABCD是菱形,
∴AD=AB=5,AC⊥BD,AO=AC=×6=3,OB=OD,
在Rt△AOD中,由勾股定理得:OD===4,
∴BD=2OD=8,
∵DE⊥BC,
∴∠DEB=90°,
∵OD=OB,
∴OE=BD=×8=4,
故答案为:4.
18.解:因为在矩形ABCD中,∠ADC=90°,
∵∠ADE:∠EDC=2:1,
∴3∠EDC=90°,
∴∠EDC=30°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DCE=60°,
∵OD=OC,
∴△ODC是等边三角形,
∴∠DOE=60°,
∴∠BDE=30°.
故答案为:30°.
19.解:方法一:如图,将△AOC绕O逆时针旋转90°,
∴∠OBD=∠OAC,
∵四边形ABEF是正方形,
∴AE⊥BF,
∴∠AOB=90°,
∵∠ACB=90°,
∴∠OAC+∠OBC=180°,
∴∠OBD+∠OBC=180°,
∴C,B,D在同一条直线上,
由旋转可知:
BD=AC=3,OD=OC=4,∠AOD=90°,
∴CD==8,
∴BC=CD﹣BD=8﹣3=5.
方法二:如图,以C为坐标原点建立直角坐标系,CB为x轴,CA为y轴,则A(0,3),
作EQ⊥x轴于点Q,OM⊥x轴于点M,
设B(x,0),由于O点为以AB一边向三角形外作正方形ABEF的中心,
∴AB=BE,∠ABE=90°,
∵∠ACB=90°,
∴∠BAC+∠ABC=90°,∠ABC+∠EBQ=90°,
∴∠BAC=∠EBQ,
在△ABC和△BEQ中,
,
∴△ACB≌△BQE(AAS),
∴AC=BQ=3,BC=EQ,
设BC=EQ=x,
∴O为AE中点,
∴OM为梯形ACQE的中位线,
∴OM=,
又∵CM=CQ=,
∴O点坐标为(,),
根据题意得:OC=4,
根据勾股定理,得
(4)2=2()2
解得x=5,
则BC=5.
故答案为:5.
20.解:延长EB至G,使BG=BE,连接CG,如图所示:
∵四边形ABCD是矩形,
∴AB∥CD,AD∥BC,
∴∠DCA=∠BAC,
∵∠DCA=∠DAF,
∴∠BAC=∠DAF,
∴∠EAF=∠DAC,
∵∠AFE=∠FAC+∠ACE,∠ACB=∠ECB+∠ACE,∠FAC=∠ECB,
∴∠AFE=∠ACB,
∵AD∥BC,
∴∠ACB=∠DAC,
∴∠EAF=∠EFA,
∴AE=EF,
∵AB⊥BC,BG=BE,
∴CG=CE,
∴∠ECB=∠GCB,
∵∠ACG=∠ACB+∠BCG,∠ACB=∠CAD,
∴∠ACG=∠DAF=∠BAC,
∴AG=CG,
又∵CE=CG,
∴CE=AG,
∴CF+EF=AE+2EB,
∴CF=2EB=4,
∴EB=2,
∴AB=AE+EB=3+2=5;
故答案为:5.
21.解:(1)四边形AECF、四边形ABCD都是平行四边形,理由如下:
∵AE⊥BD,CF⊥BD,
∴AE∥CF,
∵AF∥CE,
∴四边形AECF是平行四边形;
∴OA=OC,OE=OF,
又∵BE=DF,
∴OB=OD,
∴四边形ABCD是平行四边形;
(2)由(1)得:四边形AECF是平行四边形,
∴AE=CF,
在Rt△AEF中,AE===6,
∴CF=6,
∵BE=7,EF=8,
∴BF=BE+EF=15,
在Rt△BCF中,BC===3.
22.解:(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在Rt△ABE和Rt△DAF中,
,
∴Rt△ABE≌Rt△DAF(HL);
(2)证明:∵Rt△ABE≌Rt△DAF,
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∴BE⊥AF;
(3)∵BE⊥AF,
∵点H为BF的中点,
∴GH=BF,
∵在Rt△BCF中,BC=5,CF=CD﹣DF=5﹣2=3,根据勾股定理,得
∴BF==,
∴GH=.
23.解(1)完成图形如图①②所示,EF是线段DP的垂直平分线,
猜想:当点P运动时,∠PDE的度数不变,∠PDE=45°;
(2)证明:如图①中,过点E作MN∥BC分别交DC,AB于M,N,
则∠PNE=∠EMD=90°,
∵点E在线段DP的垂直平分线上,
∴ED=EP,
∵四边形ABCD是正方形,
∴EN=AN=DM,
在Rt△PNE和Rt△EMD中,
,
∴Rt△PNE≌Rt△EMD(HL),
∴∠PEN=∠EDM,
∵∠EDM+∠DEM=90°,
∴∠PEN+∠DEM=90°,
∴∠PED=90°,
∵ED=EP,
∴∠PDE=45°.
24.(1)证明:∵AB∥DC,
∴∠ABD=∠CDB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴BC=CD,且AB=BC,
∴CD=AB,且AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形;
(2)解:由(1)得:四边形ABCD是菱形,
∴OA=OC,BD⊥AC,BO=DO,
∵CE⊥AB,
∴AC=2OE=4,
∴OA=2,
∴OB===1,
∴BD=2OB=2,
∴菱形ABCD的面积=AC×BD=×4×2=4.
25.(1)证明:∵四边形ABCD为矩形,
∴AB=CD,AB∥CD,
∴∠BAF=∠DCE,
在△BAF和△DCE中,,
∴△DCE≌△BAF(SAS),
∴DE=BF,∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF为平行四边形;
(2)解:∵DE⊥AC,∠ADE=30°,AD=2,AF=CE,
∴CF=,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠DAC=60°,
∴∠ACD=30°,
∴AC=2AD=4,
∴EF=AC﹣AE﹣CF=4﹣1﹣1=2,
∴平行四边形DEBF的面积=2△DEF的面积=DE×EF=.
26.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
又∵BE=DF,
∴AB+BE=DC+DF,
即AE=CF.
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形.
∴AC、EF互相平分.
(2)四边形AECF是菱形.
证明:∵AB∥DC,
∴∠AEO=∠CFO.
∵EF平分∠AEC,
∴∠AEO=∠CEO.
∴∠CEO=∠CFO.
∴CE=CF.
∵四边形AECF是平行四边形,
∴四边形AECF是菱形.
27.解:(1)∵正方形ABCD的面积是8,
∴BC=CD==2,
∴BD=×2=4.
∵四边形ABCD为正方形,
∴∠DCO=∠BCO=∠CDO=∠MBN=45°,
∵CM平分∠ACD,
∴∠DCM=∠MCO=22.5°,
∴∠BMC=∠CDO+∠DCM=45°+22.5°=67.5°.
∵MN⊥CM,
∴∠CMN=90°,
∴∠BMN=90°﹣67.5°=22.5°,
∴∠BMN的度数为22..5°.
(2)∵∠MCO=22.5°,∠BCO=45°,
∴∠BCM=∠BCO+∠MCO=67.5°,
又∵∠BMC=67.5°,
∴∠BCM=∠BMC,
∴BM=BC=CD=2,
∴DM=BD﹣BM=4﹣2.
∵∠DCM=22.5°,∠BMN=22.5°,
∴∠DCM=∠BMN.
∴在△DCM和△BMN中,
,
∴△DCM≌△BMN(ASA),
∴BN=DM=4﹣2,
∴BN的长为4﹣2.
28.证明:连接BD,取BD的中点P,连接EP,FP,
∵E、F、P分别是DC、AB、BD边的中点,
∴EP是△BCD的中位线,PF是△ABD的中位线,
∴PF=AD,PF∥AD,EP=BC,EP∥BC,
∴∠H=∠PFE,∠BGF=∠FEP,
∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∴∠AHF=∠BGF.
1.下列说法正确的是( )
A.对角线互相垂直的四边形是菱形
B.矩形的对角线互相垂直
C.一组对边平行的四边形是平行四边形
D.对角线相等的平行四边形是矩形
2.平行四边形一边长是10cm,那么它的两条对角线的长度可以是( )
A.8cm和6cm
B.8cm和8cm
C.8cm和12cm
D.8cm和16cm
3.如图,在?ABCD中,BE⊥AB交对角线AC于点E.若∠1=20°,则∠2的度数为( )
A.120°
B.100°
C.110°
D.90°
4.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24
B.24
C.12
D.12
5.如图,四边形ABCD中,以对角线AC为斜边作Rt△ACE,连接BE、DE,BE⊥DE,AC,BD互相平分.若2AB=BC=4,则BD的值为( )
A.2
B.
C.3
D.4
6.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2
B.1.5
C.2.4
D.2.5
7.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3
B.2
C.4
D.2
8.如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )
A.50°
B.40°
C.30°
D.20°
9.已知坐标系中有O、A、B、C四个点,其中点O(0,0),A(3,0),B(1,1),若以O、A、B、C为顶点的四边形是平行四边形,则C的坐标是
.
10.在菱形ABCD中,两条对角线相交于点O,且AB=10cm,AC=12cm.则菱形ABCD的面积是
cm2.
11.如图,过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是
.
12.?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,则AB的长为
cm.
13.如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=3,则GE=
.
14.如图,以△ABC的边AB、AC为边往外作正方形ABEF与正方形ACGD,连接BD、CF、DF,若AB=2,AC=4,则BC2+DF2的值为
.
15.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是
.
16.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=7,则EF的长为
.
17.如图,菱形ABCD的对角线交于点O,AB=5,AC=6,DE⊥BC于点E,则OE=
.
18.如图所示,在矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=2:1,则∠BDE=
.
19.如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,且OC=4,则BC=
.
20.矩形ABCD中,E为AB边上一点,连接CE,在CE上取一点F,且∠FAC=∠ECB,∠DCA=∠DAF,若AE=3,CF=4,则AB长为
.
21.如图,在四边形ABCD中,AC、BD交于点O,AE⊥BD,CF⊥BD,E、F分别为垂足,BE=DF,AF∥CE.
(1)试判断四边形AECF、四边形ABCD形状,并说明理由;
(2)如果AF=10,EF=8,BE=7,求BC.
22.如图,已知四边形ABCD是正方形,点E、F分别在AD、DC上,BE与AF相交于点G,且BE=AF.
(1)求证:△ABE≌△DAF;
(2)求证:BE⊥AF;
(3)如果正方形ABCD的边长为5,AE=2,点H为BF的中点,连接GH.求GH的长.
23.在正方形ABCD中,点P为射线BA上的一个动点(与点B不重合).当DP的垂直平分线交线段AC于点E时,猜想:∠PDE的度数是多少?当点P运动时,∠PDE的度数是否发生改变?
请你按①如图①,点P在AB上,②如图②,点P在BA延长线上,两种情况进行探究.
(1)完成图形,写出你的猜想;
(2)选择其中的一种情况给出证明.
24.如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,OE=2,求四边形ABCD的面积.
25.如图,在矩形ABCD中,点E、F为对角线AC上两点,且AF=CE.
(1)证明:四边形DEBF为平行四边形;
(2)若DE⊥AC,∠ADE=30°,AD=2,求平行四边形DEBF的面积.
26.图,点E、F分别在?ABCD的边AB、CD的延长线上,且BE=DF,连接AC、EF、AF、CE,AC与EF交于点O.
(1)求证:AC、EF互相平分;
(2)若EF平分∠AEC,判断四边形AECF的形状并证明.
27.如图,已知正方形ABCD的面积是8,连接AC、BD交于点O,CM平分∠ACD交BD于点M,MN⊥CM,交AB于点N,
(1)求∠BMN的度数;
(2)求BN的长.
28.如图,在四边形ABCD中,AD=BC,E、F分别是边DC、AB的中点,FE的延长线分别AD、BC的延长线交于点H、G,求证:∠AHF=∠BGF.
参考答案
1.解:A、∵对角线互相垂直平分的四边形是菱形,
∴选项A不符合题意;
B、∵矩形的对角线互相平分且相等,
∴选项B不符合题意;
C、∵两组对边分别平行的四边形是平行四边形,
∴选项C不符合题意;
D、∵对角线相等的平行四边形是矩形,
∴选项D符合题意;
故选:D.
2.解:A、取对角线的一半与已知边长,得4,3,10,不能构成三角形,舍去;
B、取对角线的一半与已知边长,得4,4,10,不能构成三角形,舍去;
C、取对角线的一半与已知边长,得4,6,10,不能构成三角形,舍去;
D、取对角线的一半与已知边长,得4,8,10,能构成三角形.
故选:D.
3.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠CAB=∠1=20°,
∵BE⊥AB,
∴∠ABE=90°,
∴∠2=∠EAB+∠EBA=20°+90°=110°.
故选:C.
4.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
故选:C.
5.解:连接OE,如图所示:
∵2AB=BC=4,
∴AB=2,
∵AC,BD互相平分,
∴OA=OC,OB=OD,四边形ABCD是平行四边形,
∵以AC为斜边作Rt△ACE,
∴OE=OA=OC=AC,
∵BE⊥DE,
∴OE=OB=OD=BD,
∴AC=BD,
∴四边形ABCD是矩形,
∴AD=BC=4,∠BAD=90°,
∴BD===2,
故选:A.
6.解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM===2.4,
∴CP=EF=CM=1.2,
故选:A.
7.解:连接DN、DB,
在Rt△DAB中,∠A=90°,AB=2,AD=2,
∴BD==4,
∵点E,F分别为DM,MN的中点,
∴EF=DN,
由题意得,当点N与点B重合是DN最大,最大值为4,
∴EF长度的最大值为2,
故选:D.
8.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠EFP=×(180°﹣∠EPF)=×(180°﹣140°)=20°,
故选:D.
9.解:如图所示:
分三种情况:①AB为对角线时,点C的坐标为(4,1);
②OB为对角线时,点C的坐标为(﹣2,1);
③OA为对角线时,点C的坐标为(2,﹣1);
综上所述,点C的坐标为(4,1)或(﹣2,1)或(2,﹣1),
故答案为:(4,1)或(﹣2,1)或(2,﹣1).
10.解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=AC=6cm,OB=OD,
∴OB===8(cm),
∴BD=2OB=16cm,
∴S菱形ABCD=AC?BD=×12×16=96(cm2).
故答案为:96.
11.解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故答案为:S1=S2.
12.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,OB=OD,
又平行四边形ABCD的周长为60cm,△AOB的周长比△BOC的周长长8cm,
∴,
两个方程相加,得AB=19(cm).
故答案为:19.
13.解:取BE的中点H,连接FH、CH,如图:
∵F是AE的中点,H是BE的中点,
∴FH是△ABE的中位线,
∴FH∥AB,FH=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E是CD的中点,
∴EC=CD,
∴FH∥EC,FH=EC,
∴四边形FHCE是平行四边形,
∴GE=GH=EH.
∵BE=3,H是BE的中点,
∴EH=,
∴GE=.
故答案为:.
14.解:如图所示,连接BF,CD,
∵四边形ABEF,四边形ACGD都是正方形,
∴AB=AF,AC=AD,∠BAF=∠CAD=90°,
∴∠BAD=∠FAC,
∴△BAD≌△FAC(SAS),
∴∠ACF=∠ADB,
又∵∠AHC=∠OHD,
∴∠CAH=∠DOH=90°,
∴CF⊥BD,
∴BC2=OB2+OC2,DF2=OD2+OF2,BF2=OB2+OF2,DC2=OD2+OC2,
∴BC2+DF2=OD2+OF2+OB2+OC2,
BF2+DC2=OD2+OF2+OB2+OC2,
即BC2+DF2=BF2+DC2,
又∵△ABF和△ACD都是等腰直角三角形,且AB=2,AC=4,
∴BF2+DC2=8+32=40,
∴BC2+DF2=40,
故答案为:40.
15.解:∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC,
∵DH⊥AB,
∴DH⊥CD,∠DHB=90°,
∴OH为Rt△DHB的斜边DB上的中线,
∴OH=OD=OB,
∴∠BDH=∠DHO,
∵DH⊥CD,
∴∠BDH+∠CDO=90°,
∵BD⊥AC,
∴∠CDO+∠DCO=90°,
∴∠BDH=∠DCO,
∴∠DHO=∠DCA,
∵四边形ABCD是菱形,
∴DA=DC,
∴∠CAD=∠DCA=20°,
∴∠DHO=20°,
故答案为:20°.
16.解:∵DE为△ABC的中位线,
∴DE=BC=3.5,
在Rt△AFB中,∠AFB=90°,D是AB的中点,
∴DF=AB=2,
∴EF=DE﹣DF=1.5,
故答案为:1.5.
17.解:∵四边形ABCD是菱形,
∴AD=AB=5,AC⊥BD,AO=AC=×6=3,OB=OD,
在Rt△AOD中,由勾股定理得:OD===4,
∴BD=2OD=8,
∵DE⊥BC,
∴∠DEB=90°,
∵OD=OB,
∴OE=BD=×8=4,
故答案为:4.
18.解:因为在矩形ABCD中,∠ADC=90°,
∵∠ADE:∠EDC=2:1,
∴3∠EDC=90°,
∴∠EDC=30°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DCE=60°,
∵OD=OC,
∴△ODC是等边三角形,
∴∠DOE=60°,
∴∠BDE=30°.
故答案为:30°.
19.解:方法一:如图,将△AOC绕O逆时针旋转90°,
∴∠OBD=∠OAC,
∵四边形ABEF是正方形,
∴AE⊥BF,
∴∠AOB=90°,
∵∠ACB=90°,
∴∠OAC+∠OBC=180°,
∴∠OBD+∠OBC=180°,
∴C,B,D在同一条直线上,
由旋转可知:
BD=AC=3,OD=OC=4,∠AOD=90°,
∴CD==8,
∴BC=CD﹣BD=8﹣3=5.
方法二:如图,以C为坐标原点建立直角坐标系,CB为x轴,CA为y轴,则A(0,3),
作EQ⊥x轴于点Q,OM⊥x轴于点M,
设B(x,0),由于O点为以AB一边向三角形外作正方形ABEF的中心,
∴AB=BE,∠ABE=90°,
∵∠ACB=90°,
∴∠BAC+∠ABC=90°,∠ABC+∠EBQ=90°,
∴∠BAC=∠EBQ,
在△ABC和△BEQ中,
,
∴△ACB≌△BQE(AAS),
∴AC=BQ=3,BC=EQ,
设BC=EQ=x,
∴O为AE中点,
∴OM为梯形ACQE的中位线,
∴OM=,
又∵CM=CQ=,
∴O点坐标为(,),
根据题意得:OC=4,
根据勾股定理,得
(4)2=2()2
解得x=5,
则BC=5.
故答案为:5.
20.解:延长EB至G,使BG=BE,连接CG,如图所示:
∵四边形ABCD是矩形,
∴AB∥CD,AD∥BC,
∴∠DCA=∠BAC,
∵∠DCA=∠DAF,
∴∠BAC=∠DAF,
∴∠EAF=∠DAC,
∵∠AFE=∠FAC+∠ACE,∠ACB=∠ECB+∠ACE,∠FAC=∠ECB,
∴∠AFE=∠ACB,
∵AD∥BC,
∴∠ACB=∠DAC,
∴∠EAF=∠EFA,
∴AE=EF,
∵AB⊥BC,BG=BE,
∴CG=CE,
∴∠ECB=∠GCB,
∵∠ACG=∠ACB+∠BCG,∠ACB=∠CAD,
∴∠ACG=∠DAF=∠BAC,
∴AG=CG,
又∵CE=CG,
∴CE=AG,
∴CF+EF=AE+2EB,
∴CF=2EB=4,
∴EB=2,
∴AB=AE+EB=3+2=5;
故答案为:5.
21.解:(1)四边形AECF、四边形ABCD都是平行四边形,理由如下:
∵AE⊥BD,CF⊥BD,
∴AE∥CF,
∵AF∥CE,
∴四边形AECF是平行四边形;
∴OA=OC,OE=OF,
又∵BE=DF,
∴OB=OD,
∴四边形ABCD是平行四边形;
(2)由(1)得:四边形AECF是平行四边形,
∴AE=CF,
在Rt△AEF中,AE===6,
∴CF=6,
∵BE=7,EF=8,
∴BF=BE+EF=15,
在Rt△BCF中,BC===3.
22.解:(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在Rt△ABE和Rt△DAF中,
,
∴Rt△ABE≌Rt△DAF(HL);
(2)证明:∵Rt△ABE≌Rt△DAF,
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∴BE⊥AF;
(3)∵BE⊥AF,
∵点H为BF的中点,
∴GH=BF,
∵在Rt△BCF中,BC=5,CF=CD﹣DF=5﹣2=3,根据勾股定理,得
∴BF==,
∴GH=.
23.解(1)完成图形如图①②所示,EF是线段DP的垂直平分线,
猜想:当点P运动时,∠PDE的度数不变,∠PDE=45°;
(2)证明:如图①中,过点E作MN∥BC分别交DC,AB于M,N,
则∠PNE=∠EMD=90°,
∵点E在线段DP的垂直平分线上,
∴ED=EP,
∵四边形ABCD是正方形,
∴EN=AN=DM,
在Rt△PNE和Rt△EMD中,
,
∴Rt△PNE≌Rt△EMD(HL),
∴∠PEN=∠EDM,
∵∠EDM+∠DEM=90°,
∴∠PEN+∠DEM=90°,
∴∠PED=90°,
∵ED=EP,
∴∠PDE=45°.
24.(1)证明:∵AB∥DC,
∴∠ABD=∠CDB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴BC=CD,且AB=BC,
∴CD=AB,且AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形;
(2)解:由(1)得:四边形ABCD是菱形,
∴OA=OC,BD⊥AC,BO=DO,
∵CE⊥AB,
∴AC=2OE=4,
∴OA=2,
∴OB===1,
∴BD=2OB=2,
∴菱形ABCD的面积=AC×BD=×4×2=4.
25.(1)证明:∵四边形ABCD为矩形,
∴AB=CD,AB∥CD,
∴∠BAF=∠DCE,
在△BAF和△DCE中,,
∴△DCE≌△BAF(SAS),
∴DE=BF,∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF为平行四边形;
(2)解:∵DE⊥AC,∠ADE=30°,AD=2,AF=CE,
∴CF=,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠DAC=60°,
∴∠ACD=30°,
∴AC=2AD=4,
∴EF=AC﹣AE﹣CF=4﹣1﹣1=2,
∴平行四边形DEBF的面积=2△DEF的面积=DE×EF=.
26.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
又∵BE=DF,
∴AB+BE=DC+DF,
即AE=CF.
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形.
∴AC、EF互相平分.
(2)四边形AECF是菱形.
证明:∵AB∥DC,
∴∠AEO=∠CFO.
∵EF平分∠AEC,
∴∠AEO=∠CEO.
∴∠CEO=∠CFO.
∴CE=CF.
∵四边形AECF是平行四边形,
∴四边形AECF是菱形.
27.解:(1)∵正方形ABCD的面积是8,
∴BC=CD==2,
∴BD=×2=4.
∵四边形ABCD为正方形,
∴∠DCO=∠BCO=∠CDO=∠MBN=45°,
∵CM平分∠ACD,
∴∠DCM=∠MCO=22.5°,
∴∠BMC=∠CDO+∠DCM=45°+22.5°=67.5°.
∵MN⊥CM,
∴∠CMN=90°,
∴∠BMN=90°﹣67.5°=22.5°,
∴∠BMN的度数为22..5°.
(2)∵∠MCO=22.5°,∠BCO=45°,
∴∠BCM=∠BCO+∠MCO=67.5°,
又∵∠BMC=67.5°,
∴∠BCM=∠BMC,
∴BM=BC=CD=2,
∴DM=BD﹣BM=4﹣2.
∵∠DCM=22.5°,∠BMN=22.5°,
∴∠DCM=∠BMN.
∴在△DCM和△BMN中,
,
∴△DCM≌△BMN(ASA),
∴BN=DM=4﹣2,
∴BN的长为4﹣2.
28.证明:连接BD,取BD的中点P,连接EP,FP,
∵E、F、P分别是DC、AB、BD边的中点,
∴EP是△BCD的中位线,PF是△ABD的中位线,
∴PF=AD,PF∥AD,EP=BC,EP∥BC,
∴∠H=∠PFE,∠BGF=∠FEP,
∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∴∠AHF=∠BGF.
