浙江省高考数学模拟卷（二）（无答案）

2011试卷二
1、复数等于 （ ）
A、2 B、-2 C、-2i D、2i
2、“”是成立的 （ ）
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
3、设集合
的集合中所有元素的和与积分别为 （ ）
A、 B、 C、 D、
4、对于定义在R上的奇函数，满足，则
（ ）
A、0 B、-1 C、1 D、10
5、将函数的图像向左平移个单位后，得到函数的图像，则的图像 （ ）
A、关于原点对称 B、关于y轴对称
C、关于点对称 D、关于直线对称
6、已知函数上任一点处的切线斜率则该函数的单调减区间为 （ ）
A、 B、 C、 D、
7、关于直线有以下四个命题：
①当
②
③当
④当
其中真命题的序号是 （ ）
A、② B、③ C、①② D、③④
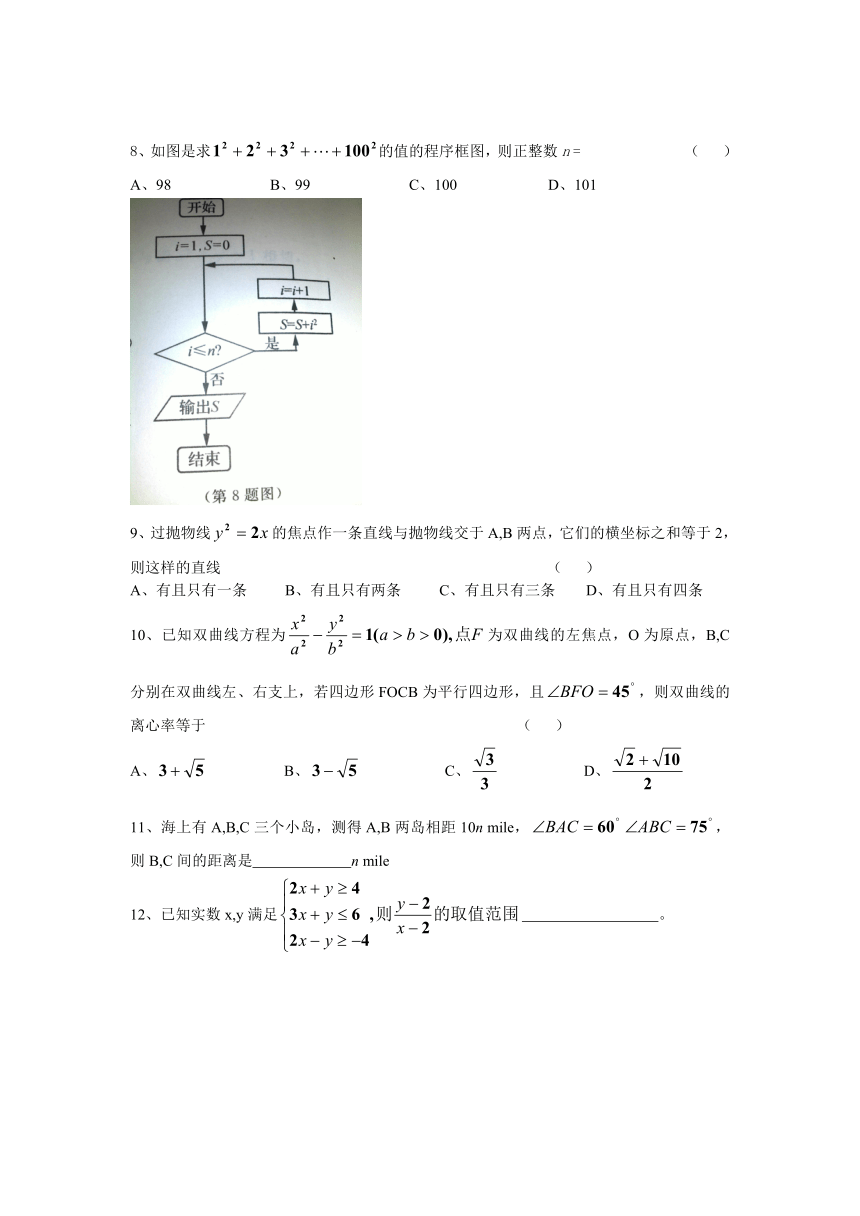
8、如图是求的值的程序框图，则正整数n = （ ）
A、98 B、99 C、100 D、101
9、过抛物线的焦点作一条直线与抛物线交于A,B两点，它们的横坐标之和等于2，则这样的直线 （ ）
A、有且只有一条 B、有且只有两条 C、有且只有三条 D、有且只有四条
10、已知双曲线方程为为双曲线的左焦点，O为原点，B,C分别在双曲线左、右支上，若四边形FOCB为平行四边形，且，则双曲线的离心率等于 （ ）
A、 B、 C、 D、
11、海上有A,B,C三个小岛，测得A,B两岛相距10n mile，，则B,C间的距离是 n mile
12、已知实数x,y满足 。
13、如图是一个正三棱柱的三视图，若三棱柱的体积是，则a= 。
14、等比数列的前n项的积为，若是一个确定的常数，那么中也是常数的是 。
15、从分别写有0，1，2，3，4的五张卡片中每一次取出一张卡片，记下数字后放回，再从中取出一张卡片。两次取出的卡片上的数字和敲好等于4的概率是 。
16、过点P（2，1）的直线分别交x轴，y轴的正半轴于A,B两点，若为坐标原点，则的最小值是 。
17、已知函数的定义域和值域都是[-1,1]( 如图所示)，函数。定义：当且时，称是方程一个实数根。则此方程的所有不同实数根的个数是 。
18、已知函数处取得最大值。
（1）求实数a的值；
（2）求函数的最小正周期和单调递增区间；
（3）若。
19、已知在数列中，，数列的奇数项依次组成公差为1的等差数列，偶数项依次组成公比为2的等比数列，数列满足，数列的前n项和为
(1)写出数列的通项公式；
(2)若对于任意的正整数n，都有恒成立，求实数a的取值范围。
20、如图，在四棱锥P—ABCD中，
为BC，PA的中点，且PA=AB=2。
（1）在线段PD上是否存在一点E，使得NM//平面ACE；若存在，求出PE的长；若不存在，说明理由。
（2）求PD与平面AMN所成的角。
21、已知函数
（1）求实数a的取值范围；
（2）若试证明：对于任意两个不相等正数恒成立。
22、如图，已知点A（1，0）和直线l：，P为l上一动点，过P作l的垂线交线段AP的垂直平分线于Q。
（1）求点Q的轨迹C的方程；
（2）已知点P（m，2）在曲线C上，过点P作曲线C的两条弦PD和PE，且PD⊥PE，判断：直线DE是否过定点？试证明你的结论。