2020-2021学年人教版八年级数学下册18.2特殊的平行四边形期中考试考前复习高频考点精准提升练习(Word版,无答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册18.2特殊的平行四边形期中考试考前复习高频考点精准提升练习(Word版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 00:08:46 | ||
图片预览

文档简介
人教版八年级下册数学《特殊的平行四边形》期中考试考前复习
高频考点精准提升练习
时间:120分钟
总分:120分
选择题.
题号
1
2
3
4
5
6
7
8
9
10
选项
1.菱形的对角线不一定具有的性质是
( )
A.互相平分
B.互相垂直
C.每一条对角线平分一组对角
D.相等
2.
如图,菱形的边长为,过点、作对角线的垂线,分别交和的延长线于点、,,则四边形的周长为(
)
A.
B.
C.
D.
3.
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE
B.BE⊥DC
C.∠ADB=90°
D.CE⊥DE
4.
如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB=(
)
A.30°
B.45°
C.22.5°
D.135°
5.
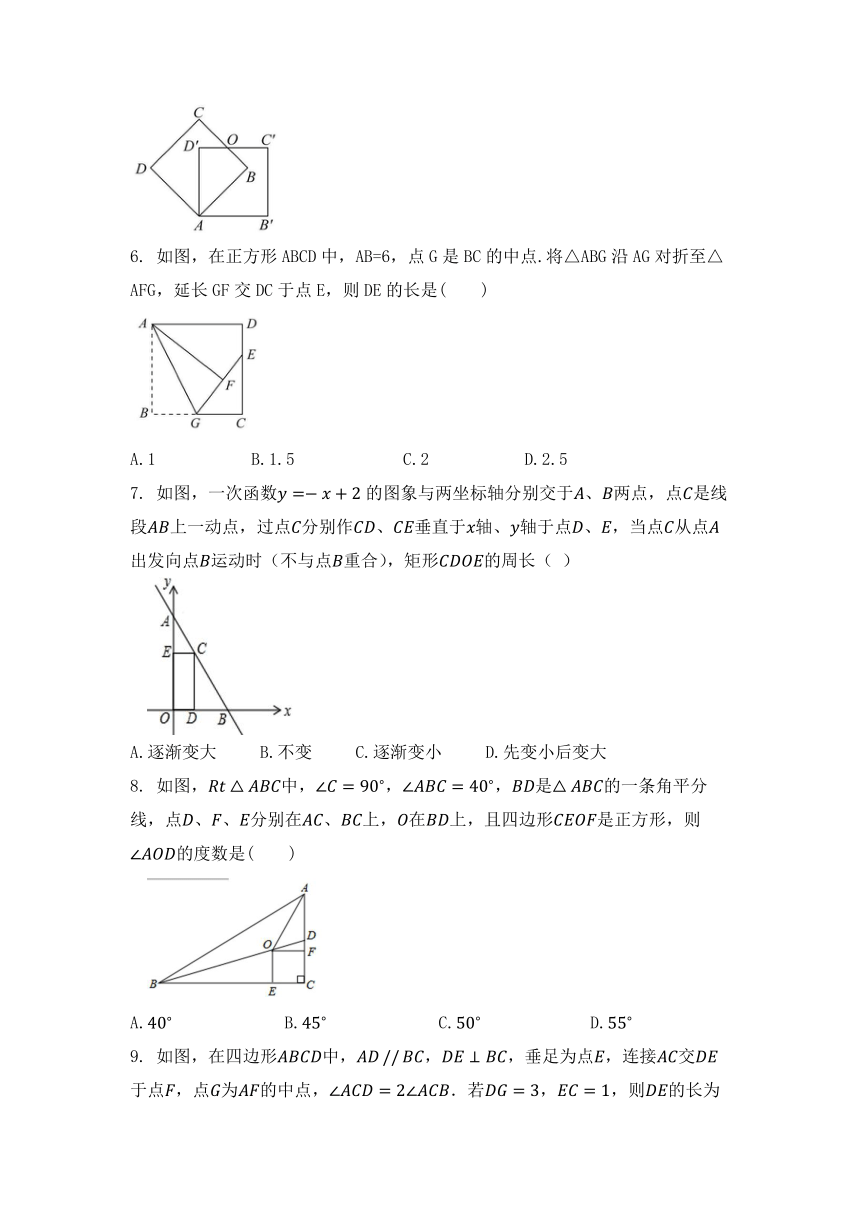
把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是
( )
6.
如图,在正方形ABCD中,AB=6,点G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( )
A.1
B.1.5
C.2
D.2.5
7.
如图,一次函数的图象与两坐标轴分别交于、两点,点是线
段上一动点,过点分别作、垂直于轴、轴于点、,当点从点
出发向点运动时(不与点重合),矩形的周长(
)
A.逐渐变大
B.不变
C.逐渐变小
D.先变小后变大
8.
如图,中,,,是的一条角平分
线,点、、分别在、上,在上,且四边形是正方形,则
的度数是( )
A.
B.
C.
D.
9.
如图,在四边形中,,,垂足为点,连接交于点,点为的中点,.若,,则的长为( )
A.
B.
C.
D.
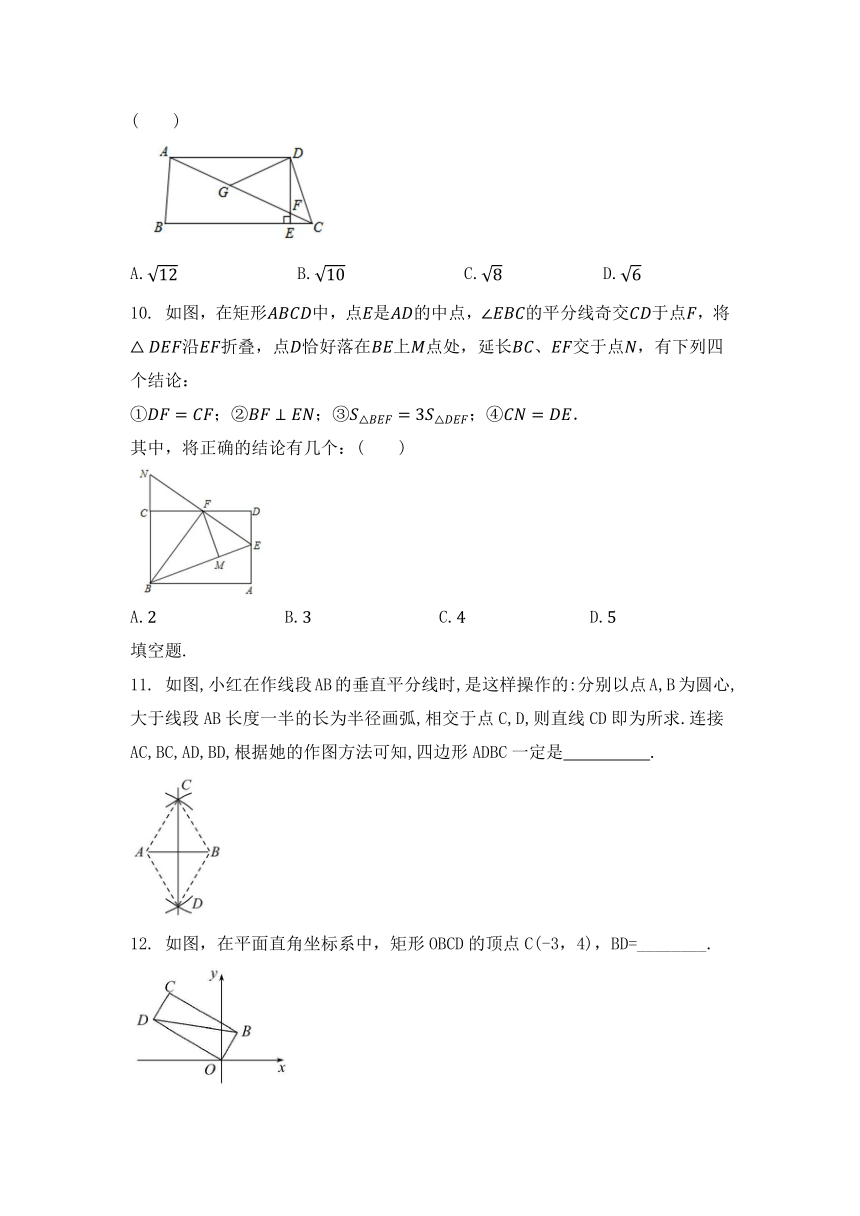
10.
如图,在矩形中,点是的中点,的平分线奇交于点,将沿折叠,点恰好落在上点处,延长、交于点,有下列四个结论:
①;②;③;④.
其中,将正确的结论有几个:( )
A.
B.
C.
D.
填空题.
11.
如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连接AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是
.
12.
如图,在平面直角坐标系中,矩形OBCD的顶点C(-3,4),BD=________.
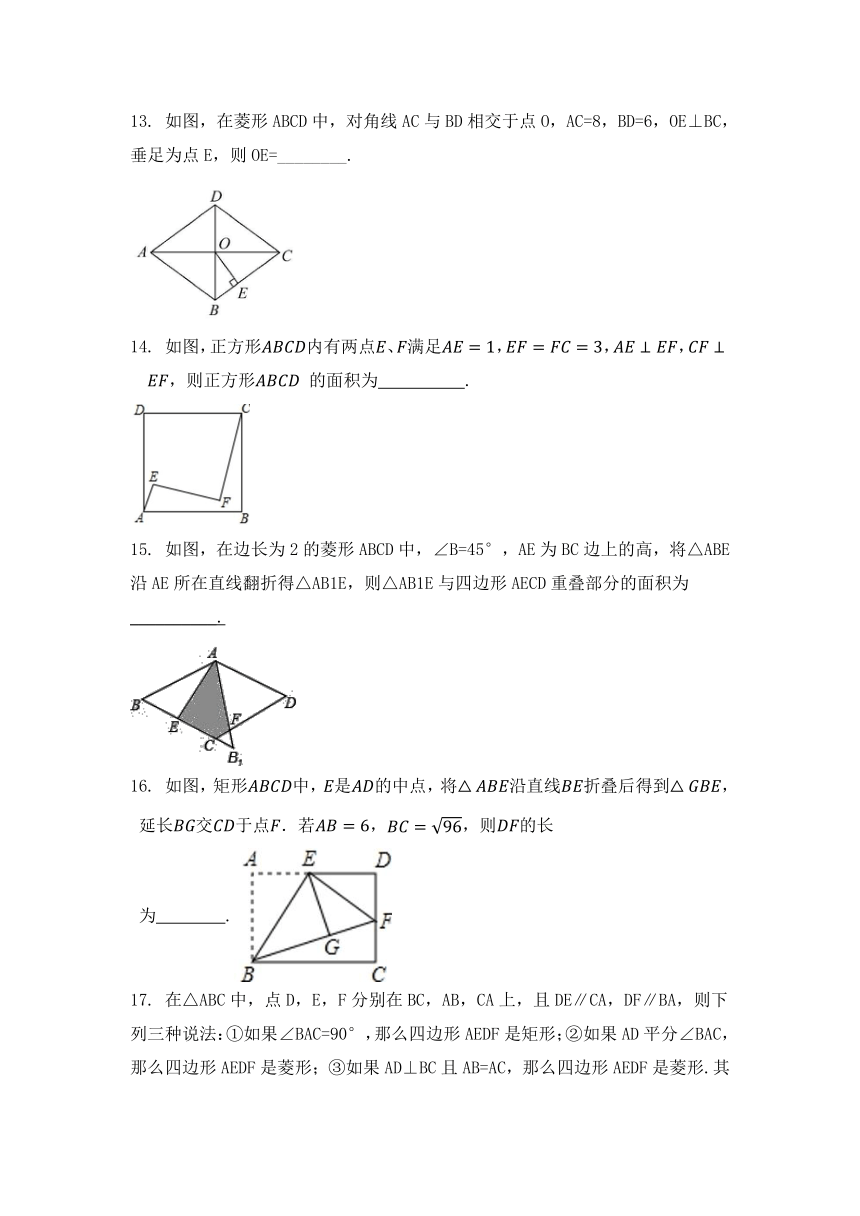
13.
如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=________.
14.
如图,正方形内有两点、满足,,,,则正方形
的面积为
.
15.
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积为__________.
16.
如图,矩形中,是的中点,将沿直线折叠后得到,延长交于点.若,,则的长为
.
17.
在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,则下列三种说法:①如果∠BAC=90°,那么四边形AEDF是矩形;②如果AD平分∠BAC,那么四边形AEDF是菱形;③如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.其中正确的有
.
18.
如图,在矩形中,,,是上异于和的任意一点,且于,于,则为
.
三.解答题.
19.
如图,矩形ABCD中,点E、F分别在AB、BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求AD的长.
20.
已知,如图,AD是△ABC的角平分线,DE∥AC,ED=AF.求证:四边形AEDF是菱形.
21.
如图所示,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
(1)求证:BE=CF;
(2)求BE的长.
22.
已知:如图,在中,是边上的一点,是的中点,过点作的平行线交于的延长线于点,且,连接.
求证:是的中点;
如果,试判断四边形的形状,并证明你的结论.
23.
(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,则有BE+DF=_______.若AB=2,则△CEF的周长为_______.?
(2)如图2,在四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
24.
如图,在四边形ABCD中,点H是边BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连接BE,CF.
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是______________,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
25.
如图,在中,,,.点从点出发
沿方向以每秒个单位长的速度向点匀速运动,同时点从点出发沿方
向以每秒个单位长的速度向点匀速运动,当其中一个点到达终点时,另一个
点也随之停止运动.设点、运动的时间是秒.过点作于点
,连接、.
求证:;
四边形能够成为菱形吗?如果能,求出相应的值;如果不能,说明理由.
当为何值时,为直角三角形?请说明理由.
?
高频考点精准提升练习
时间:120分钟
总分:120分
选择题.
题号
1
2
3
4
5
6
7
8
9
10
选项
1.菱形的对角线不一定具有的性质是
( )
A.互相平分
B.互相垂直
C.每一条对角线平分一组对角
D.相等
2.
如图,菱形的边长为,过点、作对角线的垂线,分别交和的延长线于点、,,则四边形的周长为(
)
A.
B.
C.
D.
3.
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE
B.BE⊥DC
C.∠ADB=90°
D.CE⊥DE
4.
如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB=(
)
A.30°
B.45°
C.22.5°
D.135°
5.
把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是
( )
6.
如图,在正方形ABCD中,AB=6,点G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( )
A.1
B.1.5
C.2
D.2.5
7.
如图,一次函数的图象与两坐标轴分别交于、两点,点是线
段上一动点,过点分别作、垂直于轴、轴于点、,当点从点
出发向点运动时(不与点重合),矩形的周长(
)
A.逐渐变大
B.不变
C.逐渐变小
D.先变小后变大
8.
如图,中,,,是的一条角平分
线,点、、分别在、上,在上,且四边形是正方形,则
的度数是( )
A.
B.
C.
D.
9.
如图,在四边形中,,,垂足为点,连接交于点,点为的中点,.若,,则的长为( )
A.
B.
C.
D.
10.
如图,在矩形中,点是的中点,的平分线奇交于点,将沿折叠,点恰好落在上点处,延长、交于点,有下列四个结论:
①;②;③;④.
其中,将正确的结论有几个:( )
A.
B.
C.
D.
填空题.
11.
如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连接AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是
.
12.
如图,在平面直角坐标系中,矩形OBCD的顶点C(-3,4),BD=________.
13.
如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=________.
14.
如图,正方形内有两点、满足,,,,则正方形
的面积为
.
15.
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积为__________.
16.
如图,矩形中,是的中点,将沿直线折叠后得到,延长交于点.若,,则的长为
.
17.
在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,则下列三种说法:①如果∠BAC=90°,那么四边形AEDF是矩形;②如果AD平分∠BAC,那么四边形AEDF是菱形;③如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.其中正确的有
.
18.
如图,在矩形中,,,是上异于和的任意一点,且于,于,则为
.
三.解答题.
19.
如图,矩形ABCD中,点E、F分别在AB、BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求AD的长.
20.
已知,如图,AD是△ABC的角平分线,DE∥AC,ED=AF.求证:四边形AEDF是菱形.
21.
如图所示,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
(1)求证:BE=CF;
(2)求BE的长.
22.
已知:如图,在中,是边上的一点,是的中点,过点作的平行线交于的延长线于点,且,连接.
求证:是的中点;
如果,试判断四边形的形状,并证明你的结论.
23.
(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,则有BE+DF=_______.若AB=2,则△CEF的周长为_______.?
(2)如图2,在四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
24.
如图,在四边形ABCD中,点H是边BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连接BE,CF.
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是______________,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
25.
如图,在中,,,.点从点出发
沿方向以每秒个单位长的速度向点匀速运动,同时点从点出发沿方
向以每秒个单位长的速度向点匀速运动,当其中一个点到达终点时,另一个
点也随之停止运动.设点、运动的时间是秒.过点作于点
,连接、.
求证:;
四边形能够成为菱形吗?如果能,求出相应的值;如果不能,说明理由.
当为何值时,为直角三角形?请说明理由.
?
