四年级下册数学教案-4.1.3 三角形的内角和 冀教版
文档属性
| 名称 | 四年级下册数学教案-4.1.3 三角形的内角和 冀教版 |
|
|
| 格式 | doc | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 00:00:00 | ||
图片预览


文档简介
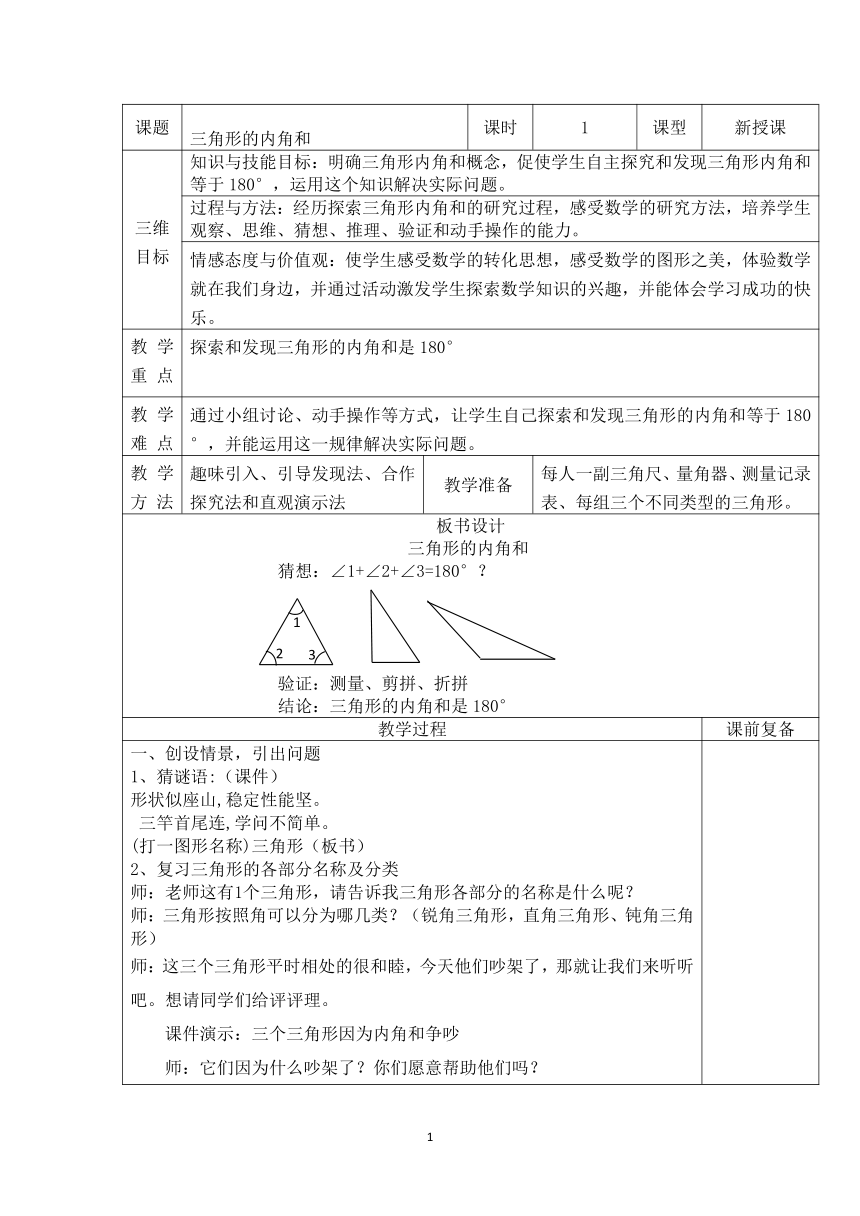
课题 三三角形的内角和 课时 1 课型 新授课
三维目标 知识与技能目标:明确三角形内角和概念,促使学生自主探究和发现三角形内角和等于180°,运用这个知识解决实际问题。
过程与方法:经历探索三角形内角和的研究过程,感受数学的研究方法,培养学生观察、思维、猜想、推理、验证和动手操作的能力。
情感态度与价值观:使学生感受数学的转化思想,感受数学的图形之美,体验数学就在我们身边,并通过活动激发学生探索数学知识的兴趣,并能体会学习成功的快乐。
教学重 点 探索和发现三角形的内角和是180°
教学难 点 通过小组讨论、动手操作等方式,让学生自己探索和发现三角形的内角和等于180°,并能运用这一规律解决实际问题。
教学方 法 趣味引入、引导发现法、合作探究法和直观演示法 教学准备 每人一副三角尺、量角器、测量记录表、每组三个不同类型的三角形。
板书设计 三角形的内角和
猜想:∠1+∠2+∠3=180°?
验证:测量、剪拼、折拼
结论:三角形的内角和是180°
教学过程 课前复备
一、创设情景,引出问题 1、猜谜语:(课件)
形状似座山,稳定性能坚。
三竿首尾连,学问不简单。
(打一图形名称)三角形(板书)
2、复习三角形的各部分名称及分类
师:老师这有1个三角形,请告诉我三角形各部分的名称是什么呢?
师:三角形按照角可以分为哪几类?(锐角三角形,直角三角形、钝角三角形)
师:这三个三角形平时相处的很和睦,今天他们吵架了,那就让我们来听听吧。想请同学们给评评理。
课件演示:三个三角形因为内角和争吵
师:它们因为什么吵架了?你们愿意帮助他们吗?
揭示课题:这节课我们就一起来研究三角形的内角和?(板书课题:三角形的内角和)
全班齐读课题
师:看到这个课题有什么想提的问题吗?(什么是三角形的内角,三角形的内角和是多少度)
老师让学生说
1、什么是三角形的内角?一个三角形有几个内角?
2、三角形的内角和指的是什么?
老师解释:三角形内的三个角就是三角形的内角,为了研究方便把内角标上1、2、3,读作∠1、∠2、∠3,∠1+∠2+∠3的度数和就是三角形的内角和。
二、合作探究
1、量一量,算一算
师:用什么方法才能求出三角形内角和是多少呢?(量角器)
你们认为量再算和的方法行吗?
师:为了探究三角形的内角和,同学们就请你们拿出手里的三角形,用量角器量一量它们每一个内角各是多少度,再分别加起来。
同桌合作:一人测量内角,一人做好真实的记录,并算出它们的和。
学生汇报:
师:三角形的内角和可能是多少度?谁来猜一猜?
你们对于所说的三角形内角和度数能不能肯定?
过渡句:知识是科学,光猜也不行,有没有什么科学的方法继续验证三角形内角和是180°的吗?
2、合作验证:剪——拼,(折——拼)
学生介绍剪拼的方法
师:把三角形的三个内角剪下来拼在一起,拼成几个角(1个)
像同学所猜测的三角形内角和是180°的话,拼成一个角,那会是什么角?(平角)平角怎么画的?(让生举起手画)
问题:把三角形的三个内角剪下来到底能不能拼成一个平角?你们想试一下吗?
师:为了节约时间,每组选择一种类型的三角形进行研究。先别着急,想一想,除了这种剪拼的方法,还有没有其它的方法可以验证三角形内角和是否是180°
小组合作:让学生把研究结果贴在展示板上
课件演示:剪——拼,折一折
师:经过操作,我们得出什么结论?(三角形内角和是180°)
思考:为什么我们用测量计算得不到统一的结果?(误差)
小结:刚才同学用剪拼、折一折的巧妙方法验证,无论是什么样的三角形内角和都是180°,你们真不错。我为你们的成功表示衷心的祝贺 ,让我们带着自豪的语气大声地读出:三角形的内角和是180°(板书:三角形的内角和是180°)
师:有了这个结论同学想对它们三个说些什么?生活也一样,有了矛盾就应该想办法化解矛盾争取一个团结合作的集体。
课堂练习设计
1、 “看图,口算未知角的的度数”。(图形题)
2、“在一个三角形中,∠1=140°,∠3=25°,求∠2的度数。”(文字题)
【设计意图:1、2两题都是检测学生对“三角形的内角和是180°”的应用。已知一般三角形两角,求一角的度数。】
3、猜猜三角精灵内角的度数。
等边三角形:一个角也不知道的情况,求三角形的内角。
直角三角形:建议学生选用求直角三角形一锐角度数的最佳方法。
钝角三角形:已知三角形的一个角,求两角的度数。
【设计意图:检测学生对“三角形的内角和是180°”与三角形的特点相结合的应用。】
6、把三角形的一个内角截去,剩下图形的内角和是多少度?
⑴过顶点截取,所剩图形是三角形,内角和是180°;
⑵不过顶点截取,所剩图形是四边形,内角和是360°.
测量法、辅助线法(最优选择)
【设计意图:检测学生对多种截法的思考以及利用“三角形的内角和是180°”推导出任意四边形的内角和】
7、你能运用所学知识求出下面图形的内角和吗?
……
课后作业设计
2
三维目标 知识与技能目标:明确三角形内角和概念,促使学生自主探究和发现三角形内角和等于180°,运用这个知识解决实际问题。
过程与方法:经历探索三角形内角和的研究过程,感受数学的研究方法,培养学生观察、思维、猜想、推理、验证和动手操作的能力。
情感态度与价值观:使学生感受数学的转化思想,感受数学的图形之美,体验数学就在我们身边,并通过活动激发学生探索数学知识的兴趣,并能体会学习成功的快乐。
教学重 点 探索和发现三角形的内角和是180°
教学难 点 通过小组讨论、动手操作等方式,让学生自己探索和发现三角形的内角和等于180°,并能运用这一规律解决实际问题。
教学方 法 趣味引入、引导发现法、合作探究法和直观演示法 教学准备 每人一副三角尺、量角器、测量记录表、每组三个不同类型的三角形。
板书设计 三角形的内角和
猜想:∠1+∠2+∠3=180°?
验证:测量、剪拼、折拼
结论:三角形的内角和是180°
教学过程 课前复备
一、创设情景,引出问题 1、猜谜语:(课件)
形状似座山,稳定性能坚。
三竿首尾连,学问不简单。
(打一图形名称)三角形(板书)
2、复习三角形的各部分名称及分类
师:老师这有1个三角形,请告诉我三角形各部分的名称是什么呢?
师:三角形按照角可以分为哪几类?(锐角三角形,直角三角形、钝角三角形)
师:这三个三角形平时相处的很和睦,今天他们吵架了,那就让我们来听听吧。想请同学们给评评理。
课件演示:三个三角形因为内角和争吵
师:它们因为什么吵架了?你们愿意帮助他们吗?
揭示课题:这节课我们就一起来研究三角形的内角和?(板书课题:三角形的内角和)
全班齐读课题
师:看到这个课题有什么想提的问题吗?(什么是三角形的内角,三角形的内角和是多少度)
老师让学生说
1、什么是三角形的内角?一个三角形有几个内角?
2、三角形的内角和指的是什么?
老师解释:三角形内的三个角就是三角形的内角,为了研究方便把内角标上1、2、3,读作∠1、∠2、∠3,∠1+∠2+∠3的度数和就是三角形的内角和。
二、合作探究
1、量一量,算一算
师:用什么方法才能求出三角形内角和是多少呢?(量角器)
你们认为量再算和的方法行吗?
师:为了探究三角形的内角和,同学们就请你们拿出手里的三角形,用量角器量一量它们每一个内角各是多少度,再分别加起来。
同桌合作:一人测量内角,一人做好真实的记录,并算出它们的和。
学生汇报:
师:三角形的内角和可能是多少度?谁来猜一猜?
你们对于所说的三角形内角和度数能不能肯定?
过渡句:知识是科学,光猜也不行,有没有什么科学的方法继续验证三角形内角和是180°的吗?
2、合作验证:剪——拼,(折——拼)
学生介绍剪拼的方法
师:把三角形的三个内角剪下来拼在一起,拼成几个角(1个)
像同学所猜测的三角形内角和是180°的话,拼成一个角,那会是什么角?(平角)平角怎么画的?(让生举起手画)
问题:把三角形的三个内角剪下来到底能不能拼成一个平角?你们想试一下吗?
师:为了节约时间,每组选择一种类型的三角形进行研究。先别着急,想一想,除了这种剪拼的方法,还有没有其它的方法可以验证三角形内角和是否是180°
小组合作:让学生把研究结果贴在展示板上
课件演示:剪——拼,折一折
师:经过操作,我们得出什么结论?(三角形内角和是180°)
思考:为什么我们用测量计算得不到统一的结果?(误差)
小结:刚才同学用剪拼、折一折的巧妙方法验证,无论是什么样的三角形内角和都是180°,你们真不错。我为你们的成功表示衷心的祝贺 ,让我们带着自豪的语气大声地读出:三角形的内角和是180°(板书:三角形的内角和是180°)
师:有了这个结论同学想对它们三个说些什么?生活也一样,有了矛盾就应该想办法化解矛盾争取一个团结合作的集体。
课堂练习设计
1、 “看图,口算未知角的的度数”。(图形题)
2、“在一个三角形中,∠1=140°,∠3=25°,求∠2的度数。”(文字题)
【设计意图:1、2两题都是检测学生对“三角形的内角和是180°”的应用。已知一般三角形两角,求一角的度数。】
3、猜猜三角精灵内角的度数。
等边三角形:一个角也不知道的情况,求三角形的内角。
直角三角形:建议学生选用求直角三角形一锐角度数的最佳方法。
钝角三角形:已知三角形的一个角,求两角的度数。
【设计意图:检测学生对“三角形的内角和是180°”与三角形的特点相结合的应用。】
6、把三角形的一个内角截去,剩下图形的内角和是多少度?
⑴过顶点截取,所剩图形是三角形,内角和是180°;
⑵不过顶点截取,所剩图形是四边形,内角和是360°.
测量法、辅助线法(最优选择)
【设计意图:检测学生对多种截法的思考以及利用“三角形的内角和是180°”推导出任意四边形的内角和】
7、你能运用所学知识求出下面图形的内角和吗?
……
课后作业设计
2
