人教版八年级数学下册17.1勾股定理课件(第一课时,共20张PPT)
文档属性
| 名称 | 人教版八年级数学下册17.1勾股定理课件(第一课时,共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 967.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 11:41:28 | ||
图片预览



文档简介
(共20张PPT)
——直角三角形三边数量关系
B
a
C
c
b
A
毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。
A、B、C的面积之间有什么关系?
SA+SB=SC
A
B
C
等腰直角三角形三边的数量关系:
a
c
b
情景引入
两直边的平方和等于斜边的平方
A
C
B
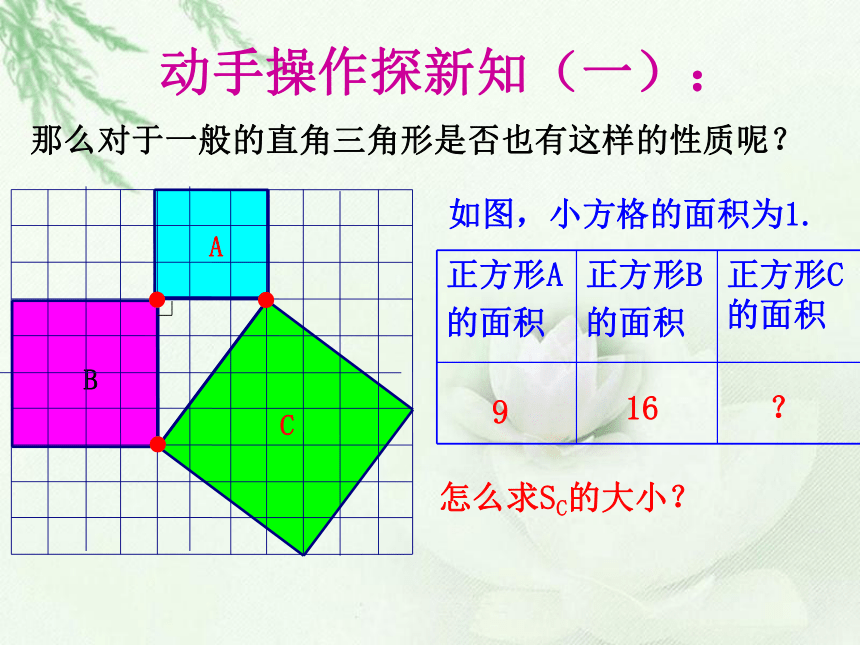
正方形A
的面积
正方形B
的面积
正方形C的面积
9
16
?
怎么求SC的大小?
如图,小方格的面积为1.
动手操作探新知(一):
那么对于一般的直角三角形是否也有这样的性质呢?
A
B
C
C
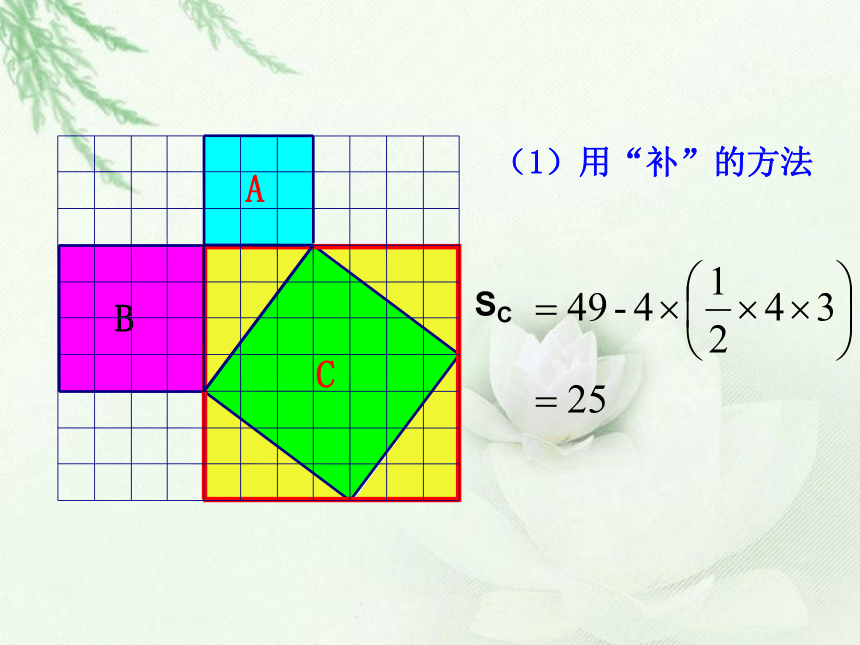
(1)用“补”的方法
SC
A
Q
C
C
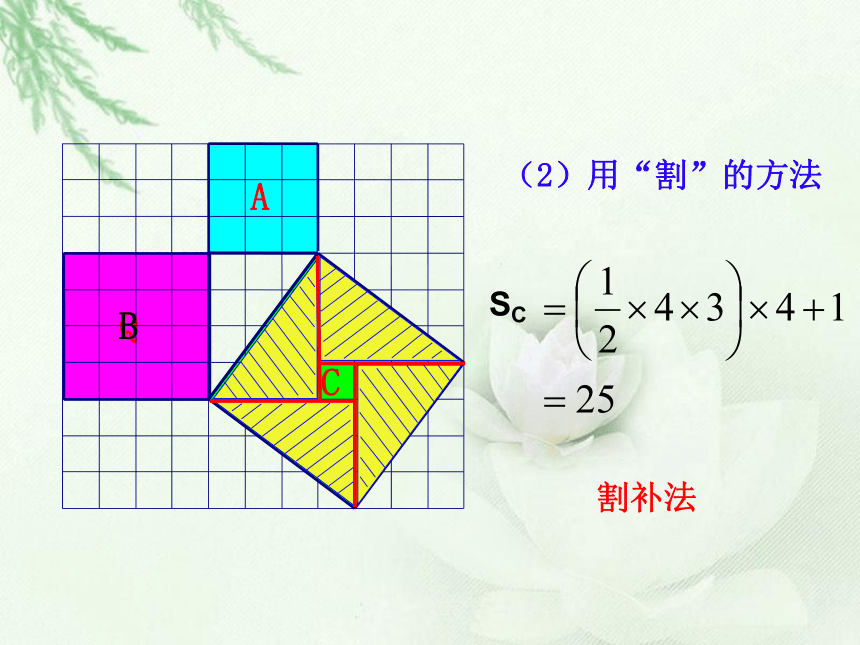
(2)用“割”的方法
B
SC
割补法
A
C
B
9
16
25
归纳总结
SA+SB=SC
A的面积
B的面积
C的面积
面积
A、B、C面积关系
直角三角形三边关系
直角三角形两直角边的平方和等于斜边的平方。
a
b
c
c
b
a
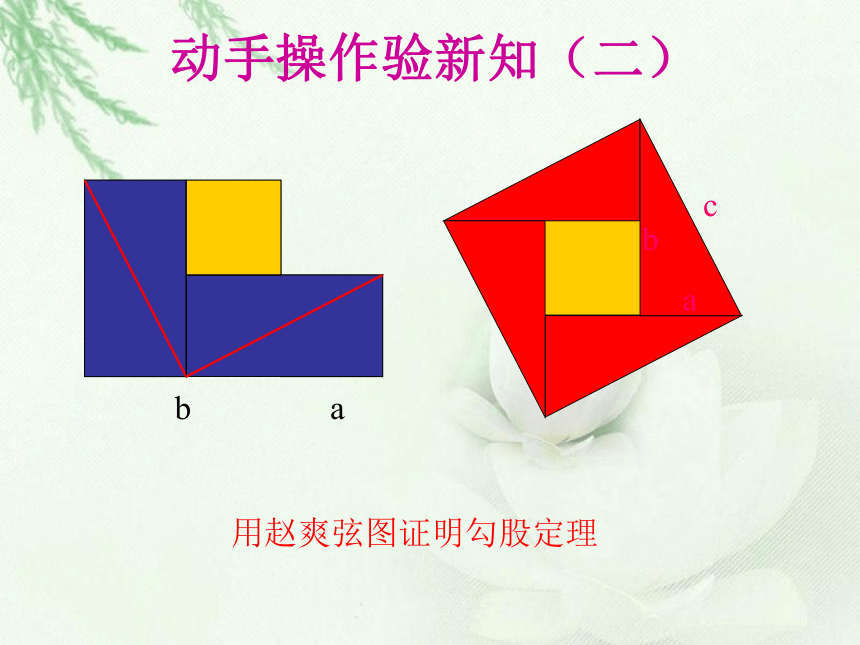
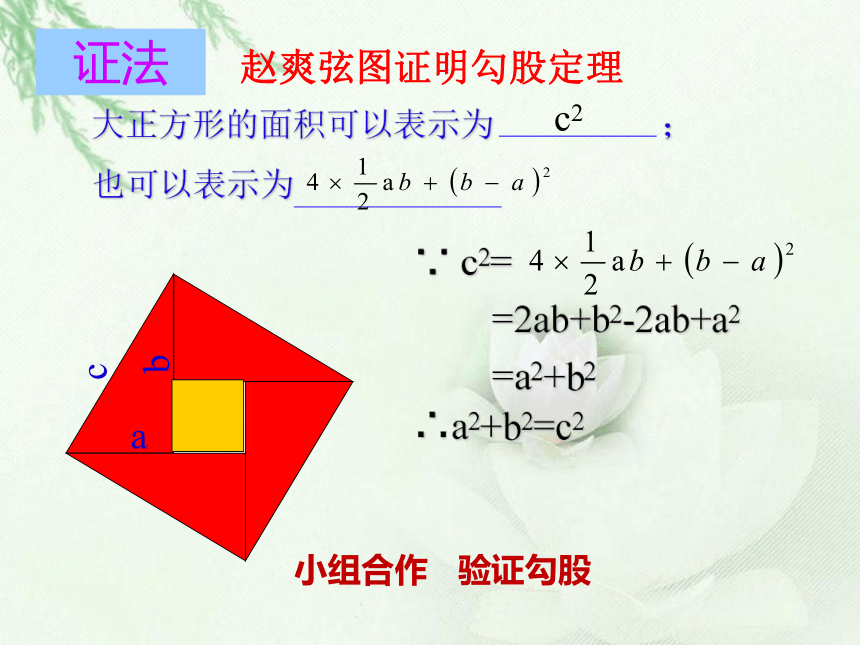
用赵爽弦图证明勾股定理
b
a
动手操作验新知(二)
c
a
b
a
∵
c2=
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为
;
也可以表示为
c2
证法
赵爽弦图证明勾股定理
小组合作
验证勾股
a2
+
b2
=
c2
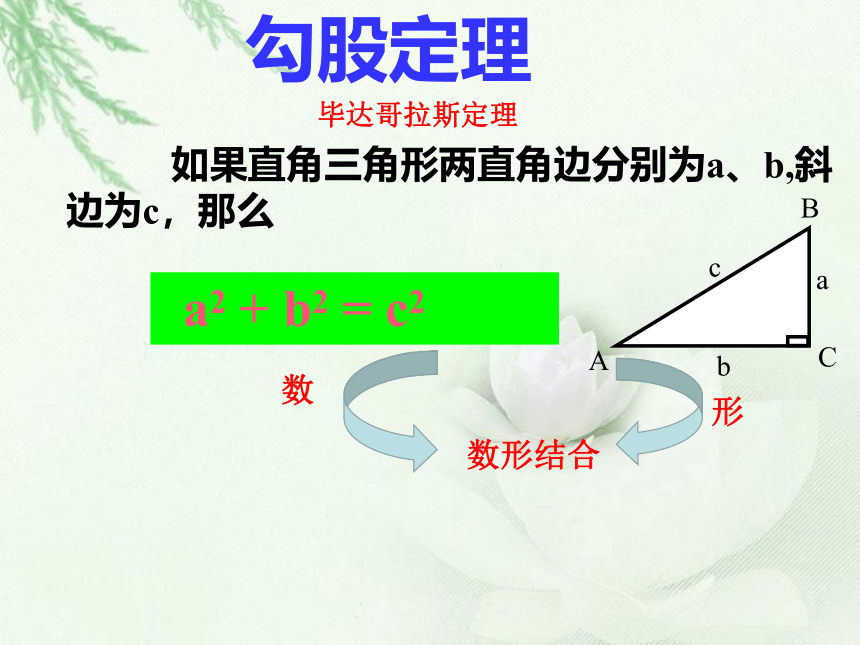
勾股定理
A
B
C
a
b
c
如果直角三角形两直角边分别为a、b,斜边为c,那么
形
数
数形结合
毕达哥拉斯定理
1.成立条件:
在直角三角形中;
3.作用:已知直角三角形任意两边长,
求第三边长.
2.公式变形:
a
b
c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾
股
定
理
在Rt△ABC中
,
根据勾股定理
(1)解:
例1:求出下列直角三角形中未知边的长度.
A
12
B
C
6
(1)
(2)
小试牛刀用新知:
A
C
B
25
7
1
2
5
4
3
1.判断题。(5分)
如果三角形中有两条边为3和4,
则第三边一定是5.(
)
×
2.
在Rt△ABC中,b
=4,c=5,
求a.(15分)
分类讨论思想
3.若直角三角形的斜边与一条直角边的和为8,另一直角边为4,求斜边的长。(15分)
方程思想
4.你真幸运不用做题就可获得10分。
5.如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D
的面积分别是4,9,1,6.求最大正方形E
的面积.
(10分)
A
B
C
D
E
1
1
美丽的勾股树
课堂小结
基本知识
1
1
基本技能
2
数学思想:
3
赵爽弦图
拼图
思想
分类讨论
方程
数形结合
勾股定理
一个定理
4
经验
论证
观察
猜想
验证
数学经验
课堂小结
(1).
必做题:
(2).选做题:查阅有关勾股定理的历史资料,关注验证勾股定理的方法.
——直角三角形三边数量关系
B
a
C
c
b
A
毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、数学家、天文学家。
A、B、C的面积之间有什么关系?
SA+SB=SC
A
B
C
等腰直角三角形三边的数量关系:
a
c
b
情景引入
两直边的平方和等于斜边的平方
A
C
B
正方形A
的面积
正方形B
的面积
正方形C的面积
9
16
?
怎么求SC的大小?
如图,小方格的面积为1.
动手操作探新知(一):
那么对于一般的直角三角形是否也有这样的性质呢?
A
B
C
C
(1)用“补”的方法
SC
A
Q
C
C
(2)用“割”的方法
B
SC
割补法
A
C
B
9
16
25
归纳总结
SA+SB=SC
A的面积
B的面积
C的面积
面积
A、B、C面积关系
直角三角形三边关系
直角三角形两直角边的平方和等于斜边的平方。
a
b
c
c
b
a
用赵爽弦图证明勾股定理
b
a
动手操作验新知(二)
c
a
b
a
∵
c2=
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为
;
也可以表示为
c2
证法
赵爽弦图证明勾股定理
小组合作
验证勾股
a2
+
b2
=
c2
勾股定理
A
B
C
a
b
c
如果直角三角形两直角边分别为a、b,斜边为c,那么
形
数
数形结合
毕达哥拉斯定理
1.成立条件:
在直角三角形中;
3.作用:已知直角三角形任意两边长,
求第三边长.
2.公式变形:
a
b
c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾
股
定
理
在Rt△ABC中
,
根据勾股定理
(1)解:
例1:求出下列直角三角形中未知边的长度.
A
12
B
C
6
(1)
(2)
小试牛刀用新知:
A
C
B
25
7
1
2
5
4
3
1.判断题。(5分)
如果三角形中有两条边为3和4,
则第三边一定是5.(
)
×
2.
在Rt△ABC中,b
=4,c=5,
求a.(15分)
分类讨论思想
3.若直角三角形的斜边与一条直角边的和为8,另一直角边为4,求斜边的长。(15分)
方程思想
4.你真幸运不用做题就可获得10分。
5.如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D
的面积分别是4,9,1,6.求最大正方形E
的面积.
(10分)
A
B
C
D
E
1
1
美丽的勾股树
课堂小结
基本知识
1
1
基本技能
2
数学思想:
3
赵爽弦图
拼图
思想
分类讨论
方程
数形结合
勾股定理
一个定理
4
经验
论证
观察
猜想
验证
数学经验
课堂小结
(1).
必做题:
(2).选做题:查阅有关勾股定理的历史资料,关注验证勾股定理的方法.
