人教版八年级数学下册17.1.2勾股定理(第二课时,共16张PPT)
文档属性
| 名称 | 人教版八年级数学下册17.1.2勾股定理(第二课时,共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 520.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 11:41:05 | ||
图片预览



文档简介
(共16张PPT)
第十七章
勾股定理
17.1
勾股定理(二)
a
b
c
A
B
C
c2
=
a2
+
b2
结论变形
a2
+
b2=
c2
a
b
c
A
B
C
如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2
+
b2=
c2
如果在Rt△
ABC中,∠C=90°,
那么
勾股定理
符号语言
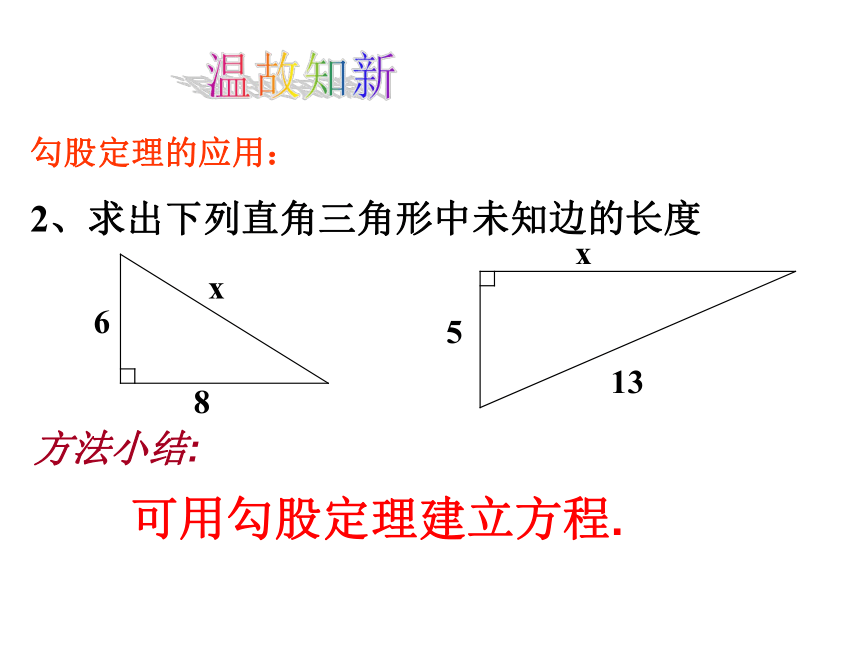
勾股定理的应用:
1、求下列图中字母所表示的正方形的面积
=625
225
400
A
225
81
B
=144
勾股定理的应用:
2、求出下列直角三角形中未知边的长度
6
8
x
5
x
13
可用勾股定理建立方程.
方法小结:
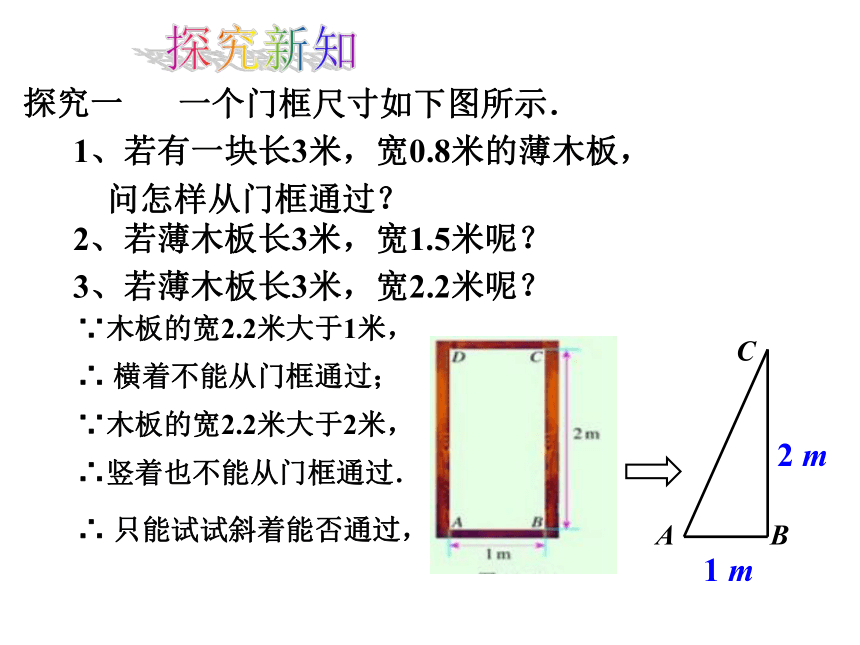
一个门框尺寸如下图所示.
1、若有一块长3米,宽0.8米的薄木板,
问怎样从门框通过?
2、若薄木板长3米,宽1.5米呢?
3、若薄木板长3米,宽2.2米呢?
A
B
C
1
m
2
m
∵木板的宽2.2米大于1米,
∴
横着不能从门框通过;
∵木板的宽2.2米大于2米,
∴竖着也不能从门框通过.
∴
只能试试斜着能否通过,
探究一
因为
大于木板的宽2.2
m,
所以木板能从门框内通过.
A
B
C
1
m
2
m
解:在Rt△ABC中,根据勾股
定理,得 AC2=AB2+BC2=12+22=5.
所以
AC=
≈2.24.
将实际问题转化为数学问
题,建立几何模型,画出图形,分
析已知量、待求量,这是解
决实际问题的一般套路.
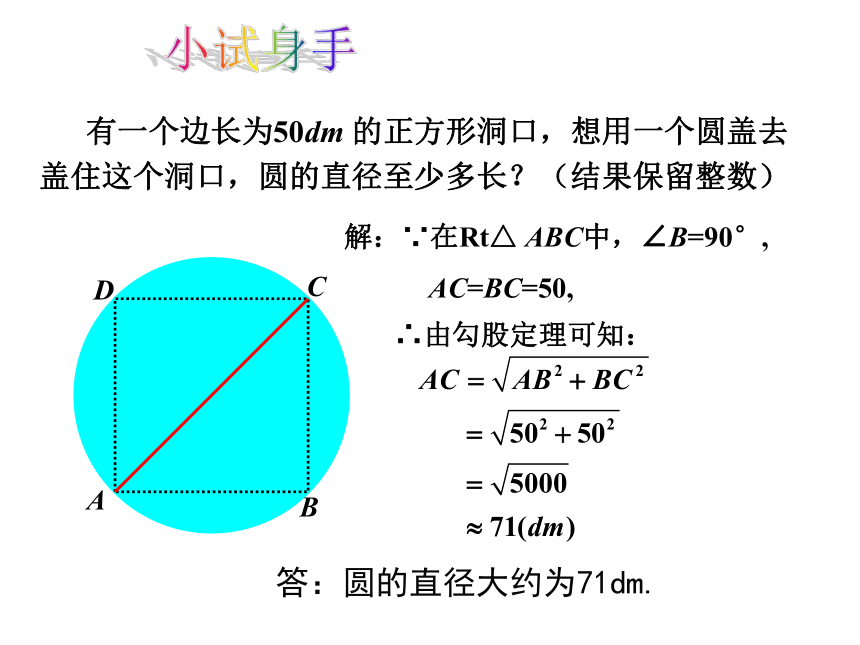
有一个边长为50dm
的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50dm
A
B
C
D
解:∵在Rt△
ABC中,∠B=90°,
AC=BC=50,
∴由勾股定理可知:
答:圆的直径大约为71dm.
探究二
一个2.6m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
E
D
(1)
图中有几个直角三角形?
(2)
分别知道了三角形的哪些边?可以求哪些边的长?
【分析】
(3)
题目中需要求哪条线段的长?
解:在Rt△ABC中,
∵∠ACB=90°
∴BC2=AB2-
AC2=2.62-2.42=1
∴BC=1
m
由题意得:DE=AB=2.6m
DC=AC-AD=2.4-0.5=1.9
m
在Rt△DCE中,
∴BE=CE-BC=1.77-1=0.77≠0.5m
答
梯子底端B外移了0.77m而不是0.5
m。
∵∠DCE=90°
∴
CE2=DE2-DC2=2.62-1.92=3.15
∴CE≈1.77
m
E
D
1.
如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,现在测得CB=60
m,AC=
20
m
,请你求出A、B两点间的距离。
B
A
60
20
C
2.
如图在平面直角坐标系中有两点
A(5,0)和B(0,4),
求这两点之间的距离.
A
B
1、
如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
C
A
E
B
D
15
10
x
25-x
解:设AE=
x
km,
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又
∵
DE=CE
∴
AD2+AE2=
BC2+BE2
即:152+x2=102+(25-x)2
答:E站应建在离A站10km处。
∴
X=10
则
BE=(25-x)km
C
A
E
B
D
15
10
2、矩形ABCD如图折叠,使点D落在BC边上的
点F处,已知AB=8,BC=10,求CE的长。
解:设CE为X,
则DE=EF=
(8-
X).
由题意可知:
AF=AD=10,
10
10
A
B
C
D
F
E
8
6
4
说一说,这节课你有什么收获?
1.
勾股定理的作用——它把直角三角形的图形特征转化为边的数量关系.
2.
会用勾股定理进行有关计算和证明,要注意利用方程的思想求有关三角形的边长.
3.
会从实际问题中抽象出数学模型,从而解决实际问题.
1.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是
米。
2.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得BC=50米,∠B=60°,则江面的宽度为
。
3.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了400米,看到了一棵红叶树,这棵红叶树的离地面的高度是
米。
4.一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ=
厘米。
18
20
教材第28
页习题第2、3、4、5题.
第十七章
勾股定理
17.1
勾股定理(二)
a
b
c
A
B
C
c2
=
a2
+
b2
结论变形
a2
+
b2=
c2
a
b
c
A
B
C
如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2
+
b2=
c2
如果在Rt△
ABC中,∠C=90°,
那么
勾股定理
符号语言
勾股定理的应用:
1、求下列图中字母所表示的正方形的面积
=625
225
400
A
225
81
B
=144
勾股定理的应用:
2、求出下列直角三角形中未知边的长度
6
8
x
5
x
13
可用勾股定理建立方程.
方法小结:
一个门框尺寸如下图所示.
1、若有一块长3米,宽0.8米的薄木板,
问怎样从门框通过?
2、若薄木板长3米,宽1.5米呢?
3、若薄木板长3米,宽2.2米呢?
A
B
C
1
m
2
m
∵木板的宽2.2米大于1米,
∴
横着不能从门框通过;
∵木板的宽2.2米大于2米,
∴竖着也不能从门框通过.
∴
只能试试斜着能否通过,
探究一
因为
大于木板的宽2.2
m,
所以木板能从门框内通过.
A
B
C
1
m
2
m
解:在Rt△ABC中,根据勾股
定理,得 AC2=AB2+BC2=12+22=5.
所以
AC=
≈2.24.
将实际问题转化为数学问
题,建立几何模型,画出图形,分
析已知量、待求量,这是解
决实际问题的一般套路.
有一个边长为50dm
的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50dm
A
B
C
D
解:∵在Rt△
ABC中,∠B=90°,
AC=BC=50,
∴由勾股定理可知:
答:圆的直径大约为71dm.
探究二
一个2.6m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
E
D
(1)
图中有几个直角三角形?
(2)
分别知道了三角形的哪些边?可以求哪些边的长?
【分析】
(3)
题目中需要求哪条线段的长?
解:在Rt△ABC中,
∵∠ACB=90°
∴BC2=AB2-
AC2=2.62-2.42=1
∴BC=1
m
由题意得:DE=AB=2.6m
DC=AC-AD=2.4-0.5=1.9
m
在Rt△DCE中,
∴BE=CE-BC=1.77-1=0.77≠0.5m
答
梯子底端B外移了0.77m而不是0.5
m。
∵∠DCE=90°
∴
CE2=DE2-DC2=2.62-1.92=3.15
∴CE≈1.77
m
E
D
1.
如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,现在测得CB=60
m,AC=
20
m
,请你求出A、B两点间的距离。
B
A
60
20
C
2.
如图在平面直角坐标系中有两点
A(5,0)和B(0,4),
求这两点之间的距离.
A
B
1、
如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
C
A
E
B
D
15
10
x
25-x
解:设AE=
x
km,
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又
∵
DE=CE
∴
AD2+AE2=
BC2+BE2
即:152+x2=102+(25-x)2
答:E站应建在离A站10km处。
∴
X=10
则
BE=(25-x)km
C
A
E
B
D
15
10
2、矩形ABCD如图折叠,使点D落在BC边上的
点F处,已知AB=8,BC=10,求CE的长。
解:设CE为X,
则DE=EF=
(8-
X).
由题意可知:
AF=AD=10,
10
10
A
B
C
D
F
E
8
6
4
说一说,这节课你有什么收获?
1.
勾股定理的作用——它把直角三角形的图形特征转化为边的数量关系.
2.
会用勾股定理进行有关计算和证明,要注意利用方程的思想求有关三角形的边长.
3.
会从实际问题中抽象出数学模型,从而解决实际问题.
1.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是
米。
2.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得BC=50米,∠B=60°,则江面的宽度为
。
3.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了400米,看到了一棵红叶树,这棵红叶树的离地面的高度是
米。
4.一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ=
厘米。
18
20
教材第28
页习题第2、3、4、5题.
