2020-2021学年北师大版七年级下册2.3平行线的性质课件(16张ppt)
文档属性
| 名称 | 2020-2021学年北师大版七年级下册2.3平行线的性质课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 229.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 11:46:04 | ||
图片预览




文档简介
(共16张PPT)
第二章 相交线与平行线
北师版
2.3-平行线的性质
数学
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
一、知识回顾
平行线的判定:
定理1:同位角相等,两直线平行.
定理2:内错角相等,两直线平行.
定理3:同旁内角角互补,两直线平行.
公理1:平行于同一条直线的两条直线平行.
公理2:在同一平面内,垂直于同一条直线的两条直线平行.
几何语言?
旧知回顾
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
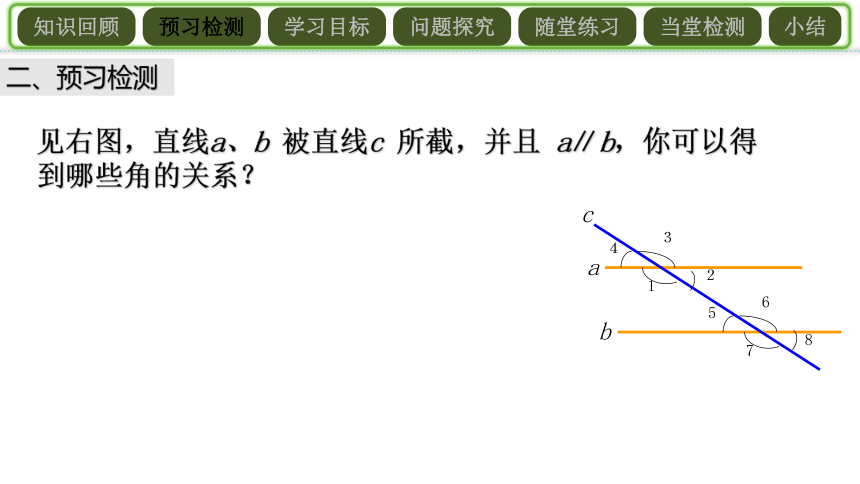
二、预习检测
见右图,直线a、b
被直线c
所截,并且
a∥b,你可以得到哪些角的关系?
b
4
3
1
2
5
6
7
8
a
c
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
三、学习目标
1.
探究平行线的性质,并理解推理过程
2.
掌握平行线性质的几何语言的书写
3.
能利用平行线的性质进行综合运用
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
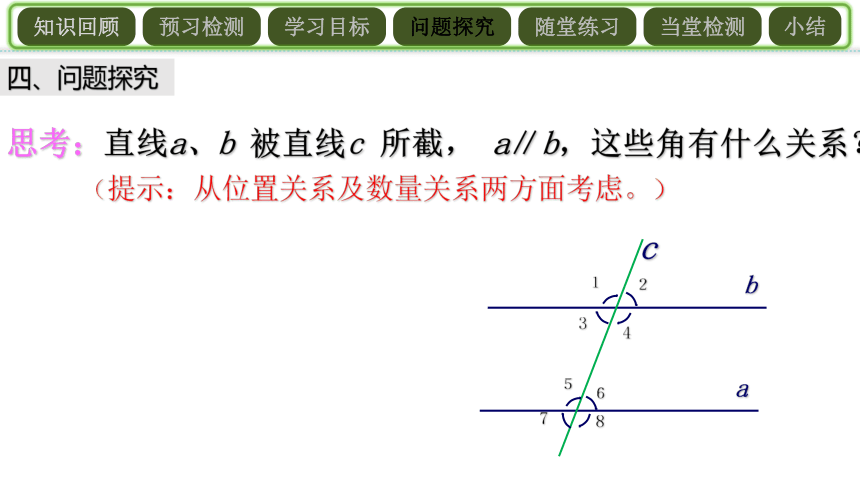
四、问题探究
思考:直线a、b
被直线c
所截,
a∥b,这些角有什么关系?
(提示:从位置关系及数量关系两方面考虑。)
c
2
1
4
6
5
7
8
3
b
a
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
b
1
2
3
4
5
6
7
8
a
c
问题1:如图,a//b,同位角有什么关系?
【1】两直线平行,同位角相等
几何语言:
∵
a∥b
(已知)
∴∠1=∠5、∠2=∠6
∠3=∠7、∠4=∠8(两直线平行,同位角相等)
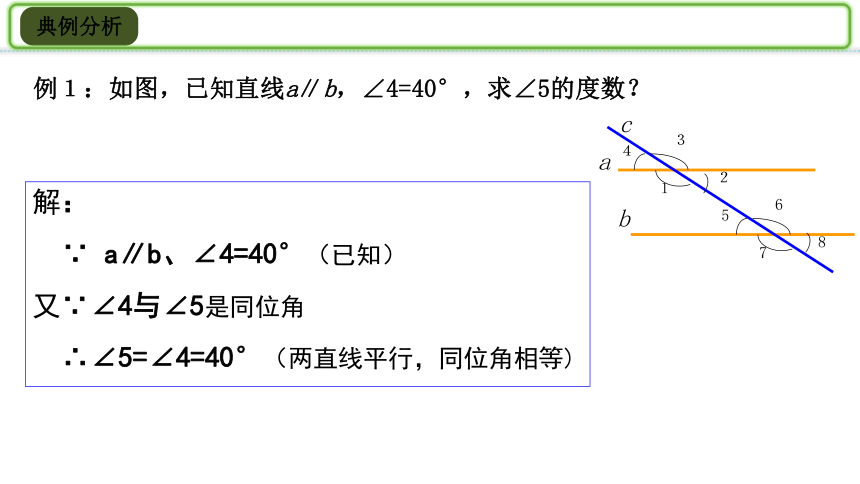
典例分析
例1:如图,已知直线a∥b,∠4=40°,求∠5的度数?
b
4
3
1
2
5
6
7
8
a
c
解:
∵
a∥b、∠4=40°(已知)
又∵∠4与∠5是同位角
∴∠5=∠4=40°(两直线平行,同位角相等)
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
b
1
2
3
4
5
6
7
8
a
c
问题2:如图,a//b,内错角有什么关系呢?
【2】两直线平行,内错角相等
定理判定:
∵a∥b(已知)
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1=∠4(对顶角相等)
∴∠4=
∠5
几何语言:
∵a∥b(已知)
∴∠4=∠5、∠3=∠6(两直线平行,内错角相等)
典例分析
例2:如图,已知直线a∥b,∠4=40°,求∠6的度数?
b
4
3
1
2
5
6
7
8
a
c
解:
∵∠4=40°(已知)
∴∠1=
180°-∠4
=140°(平角的性质)
又∵
a∥b(已知)
∴∠1=∠6
=140°(两直线平行,内错角相等)
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
问题3:如图,a//b,同旁内角有什么关系呢?
【3】两直线平行,同旁内角互补
定理判定:
∵a∥b(已知)
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1+
∠3=180°(平角的性质)
∴∠3+∠5=180°
几何语言:
∵a∥b(已知)
∴∠3+∠5=180°,∠4+∠6=180°(两直线平行,同旁内角互补)
b
1
2
3
4
5
6
7
8
a
c
典例分析
例3:如图,已知直线a∥b,∠5=40°,求∠1的度数?
b
4
3
1
2
5
6
7
8
a
c
解:
∵∠5=40°(已知)
又∵∠5与∠1是同旁内角
∴∠5+∠1=180°(两直线平行,同旁内角互补)
∴∠1=
180°-
40°=
140°
两条平行线被第三条直线所截的八个角,
已知一个,可以求出其余的七个角。
有发现吗?能够求出图中的其余所有角吗?
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
五、随堂练习
如右图,在四边形ABCD中,已知AB//CD,∠B=60?,请求∠C
的度数?能否求得∠A的度数?
A
B
C
D
解:∵AB//CD
(已知)
∴∠B+∠C=180°(两直线平行,
同旁内角互补)
∴
∠C=
180°-
∠
B
=
120
°
根据已知条件,无法求得∠A的度数。
归纳总结
平行线的3个性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的3个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
六、当堂检测
检测:已知∠C=∠AED,BE平分∠ABC;证明:
∠DBE=∠DEB.
证明:∵∠C
=∠1(已知)
∴BC
∥DE(同位角相等,两直线平行)
∴∠2=∠3(两直线平行,内错角角相等)
又∵BE
平分∠ABC
∴∠3=∠4(角平分线的性质)
∴∠2=∠4
∴∠DBE
=∠DEB
A
B
C
D
E
1
2
3
4
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
七、小结
1、上节课学的平行线的判定
“3定理、2公理”
定理1:同位角相等,两直线平行.
定理2:内错角相等,两直线平行.
定理3:同旁内角角互补,两直线平行.
公理1:平行于同一条直线的两条直线平行.
公理2:在同一平面内,垂直于同一条直线的两条直线平行.
2、本节课学的平行线的性质
“3个”
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角角互补.
3、几何语言的正确书写!
布置作业
【1】A类作业:
1号学生——(课本53页-1、2题,54页1~3题)
【2】B类作业:
2号学生——(课本53页-1、2题,54页1~4题)
【3】C类作业:
3号学生——(课本53页-1、2题,54页1~6题)
第二章 相交线与平行线
北师版
2.3-平行线的性质
数学
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
一、知识回顾
平行线的判定:
定理1:同位角相等,两直线平行.
定理2:内错角相等,两直线平行.
定理3:同旁内角角互补,两直线平行.
公理1:平行于同一条直线的两条直线平行.
公理2:在同一平面内,垂直于同一条直线的两条直线平行.
几何语言?
旧知回顾
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
二、预习检测
见右图,直线a、b
被直线c
所截,并且
a∥b,你可以得到哪些角的关系?
b
4
3
1
2
5
6
7
8
a
c
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
三、学习目标
1.
探究平行线的性质,并理解推理过程
2.
掌握平行线性质的几何语言的书写
3.
能利用平行线的性质进行综合运用
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
四、问题探究
思考:直线a、b
被直线c
所截,
a∥b,这些角有什么关系?
(提示:从位置关系及数量关系两方面考虑。)
c
2
1
4
6
5
7
8
3
b
a
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
b
1
2
3
4
5
6
7
8
a
c
问题1:如图,a//b,同位角有什么关系?
【1】两直线平行,同位角相等
几何语言:
∵
a∥b
(已知)
∴∠1=∠5、∠2=∠6
∠3=∠7、∠4=∠8(两直线平行,同位角相等)
典例分析
例1:如图,已知直线a∥b,∠4=40°,求∠5的度数?
b
4
3
1
2
5
6
7
8
a
c
解:
∵
a∥b、∠4=40°(已知)
又∵∠4与∠5是同位角
∴∠5=∠4=40°(两直线平行,同位角相等)
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
b
1
2
3
4
5
6
7
8
a
c
问题2:如图,a//b,内错角有什么关系呢?
【2】两直线平行,内错角相等
定理判定:
∵a∥b(已知)
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1=∠4(对顶角相等)
∴∠4=
∠5
几何语言:
∵a∥b(已知)
∴∠4=∠5、∠3=∠6(两直线平行,内错角相等)
典例分析
例2:如图,已知直线a∥b,∠4=40°,求∠6的度数?
b
4
3
1
2
5
6
7
8
a
c
解:
∵∠4=40°(已知)
∴∠1=
180°-∠4
=140°(平角的性质)
又∵
a∥b(已知)
∴∠1=∠6
=140°(两直线平行,内错角相等)
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
问题3:如图,a//b,同旁内角有什么关系呢?
【3】两直线平行,同旁内角互补
定理判定:
∵a∥b(已知)
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1+
∠3=180°(平角的性质)
∴∠3+∠5=180°
几何语言:
∵a∥b(已知)
∴∠3+∠5=180°,∠4+∠6=180°(两直线平行,同旁内角互补)
b
1
2
3
4
5
6
7
8
a
c
典例分析
例3:如图,已知直线a∥b,∠5=40°,求∠1的度数?
b
4
3
1
2
5
6
7
8
a
c
解:
∵∠5=40°(已知)
又∵∠5与∠1是同旁内角
∴∠5+∠1=180°(两直线平行,同旁内角互补)
∴∠1=
180°-
40°=
140°
两条平行线被第三条直线所截的八个角,
已知一个,可以求出其余的七个角。
有发现吗?能够求出图中的其余所有角吗?
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
五、随堂练习
如右图,在四边形ABCD中,已知AB//CD,∠B=60?,请求∠C
的度数?能否求得∠A的度数?
A
B
C
D
解:∵AB//CD
(已知)
∴∠B+∠C=180°(两直线平行,
同旁内角互补)
∴
∠C=
180°-
∠
B
=
120
°
根据已知条件,无法求得∠A的度数。
归纳总结
平行线的3个性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的3个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
六、当堂检测
检测:已知∠C=∠AED,BE平分∠ABC;证明:
∠DBE=∠DEB.
证明:∵∠C
=∠1(已知)
∴BC
∥DE(同位角相等,两直线平行)
∴∠2=∠3(两直线平行,内错角角相等)
又∵BE
平分∠ABC
∴∠3=∠4(角平分线的性质)
∴∠2=∠4
∴∠DBE
=∠DEB
A
B
C
D
E
1
2
3
4
知识回顾
预习检测
学习目标
问题探究
随堂练习
当堂检测
小结
七、小结
1、上节课学的平行线的判定
“3定理、2公理”
定理1:同位角相等,两直线平行.
定理2:内错角相等,两直线平行.
定理3:同旁内角角互补,两直线平行.
公理1:平行于同一条直线的两条直线平行.
公理2:在同一平面内,垂直于同一条直线的两条直线平行.
2、本节课学的平行线的性质
“3个”
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角角互补.
3、几何语言的正确书写!
布置作业
【1】A类作业:
1号学生——(课本53页-1、2题,54页1~3题)
【2】B类作业:
2号学生——(课本53页-1、2题,54页1~4题)
【3】C类作业:
3号学生——(课本53页-1、2题,54页1~6题)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
