第十一章 机械振动(B)卷 自测卷 Word版含解析
文档属性
| 名称 | 第十一章 机械振动(B)卷 自测卷 Word版含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 509.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-14 18:12:09 | ||
图片预览


文档简介
2020-2021学年高二物理人教版选修3-4
机械振动(B)卷
1.一弹簧振子做简谐运动,周期为T,下列说法正确的是( )
A.若t时刻和时刻振子相对平衡位置的位移大小相等,方向相同,则一定等于T的整数倍
B.若t时刻和时刻振子运动速度大小相等,方向相反,则一定等于的整数倍
C.若,则t和两时刻,振子的位移大小之和一定等于振幅
D.若,则在t时刻和时刻振子速度的大小一定相等
2.一位游客在千岛湖边欲乘坐游船,当日风浪较大,游船上下浮动。可把游船浮动简化成竖直方向的简谐运动,振幅为20 cm,周期为3.0 s。当船上升到最高点时,甲板刚好与码头地面平齐。地面与甲板的高度差不超过10 cm时,游客能舒服地登船。在一个周期内,游客能舒服登船的时间是( )
A.0.5 s B.0.75 s C.1.0 s D.1.5 s
3.如图,一个质量为m的木块放在质量为M的平板小车上,它们之间的最大静摩擦力是,在劲度系数为k的轻质弹簧作用下,沿光滑水平面做简谐运动,为使小车能跟木块一起振动,不发生相对滑动,则简谐运动的振幅不能大于( )
A. B. C. D.
4.在科学研究中,科学家常将未知现象同已知现象进行比较,找出其共同点,进一步推测未知现象的特性和规律。法国物理学家库仑在研究异种电荷的吸引力问题时,曾将扭秤的振动周期与电荷间距离的关系类比单摆的振动周期与摆球到地心距离的关系。已知单摆摆长为,引力常量为G,地球质量为M,摆球到地心的距离为r,则单摆振动周期T与距离r的关系式为( )
A. B. C. D.
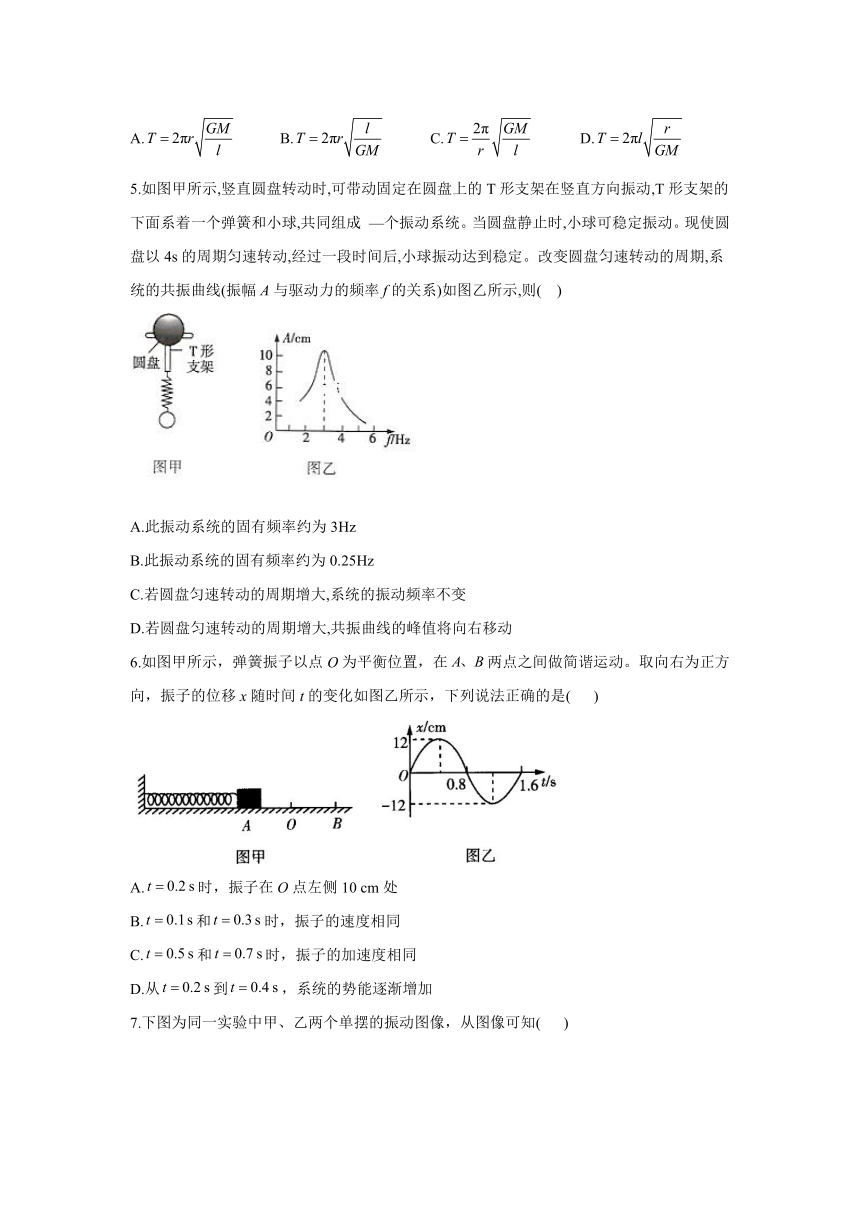
5.如图甲所示,竖直圆盘转动时,可带动固定在圆盘上的T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球,共同组成 —个振动系统。当圆盘静止时,小球可稳定振动。现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定。改变圆盘匀速转动的周期,系统的共振曲线(振幅A与驱动力的频率f的关系)如图乙所示,则(?? )
A.此振动系统的固有频率约为3Hz
B.此振动系统的固有频率约为0.25Hz
C.若圆盘匀速转动的周期增大,系统的振动频率不变
D.若圆盘匀速转动的周期增大,共振曲线的峰值将向右移动
6.如图甲所示,弹簧振子以点O为平衡位置,在两点之间做简谐运动。取向右为正方向,振子的位移x随时间t的变化如图乙所示,下列说法正确的是( )
A.时,振子在O点左侧10 cm处
B.和时,振子的速度相同
C.和时,振子的加速度相同
D.从到,系统的势能逐渐增加
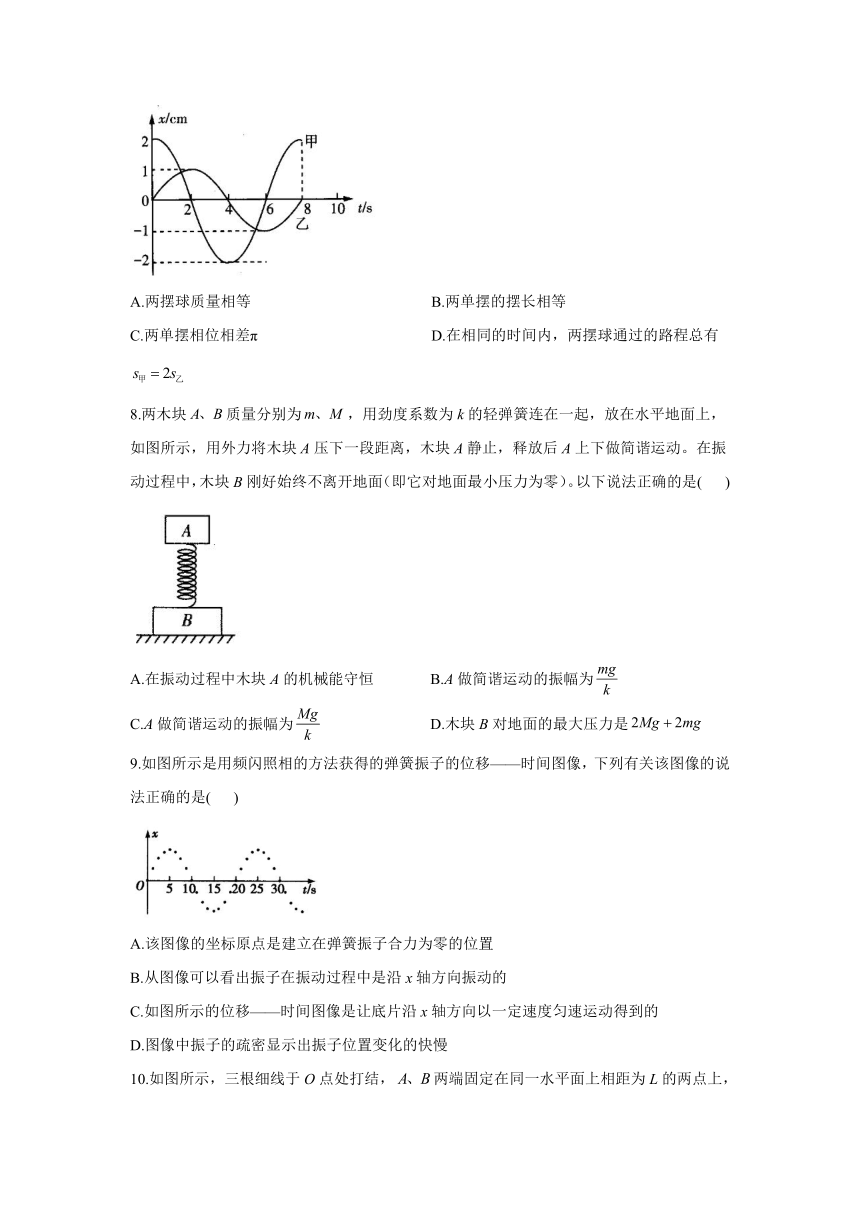
7.下图为同一实验中甲、乙两个单摆的振动图像,从图像可知( )
A.两摆球质量相等 B.两单摆的摆长相等
C.两单摆相位相差π D.在相同的时间内,两摆球通过的路程总有
8.两木块质量分别为,用劲度系数为k的轻弹簧连在一起,放在水平地面上,如图所示,用外力将木块A压下一段距离,木块A静止,释放后A上下做简谐运动。在振动过程中,木块B刚好始终不离开地面(即它对地面最小压力为零)。以下说法正确的是( )
A.在振动过程中木块A的机械能守恒 B.A做简谐运动的振幅为
C.A做简谐运动的振幅为 D.木块B对地面的最大压力是
9.如图所示是用频闪照相的方法获得的弹簧振子的位移——时间图像,下列有关该图像的说法正确的是( )
A.该图像的坐标原点是建立在弹簧振子合力为零的位置
B.从图像可以看出振子在振动过程中是沿x轴方向振动的
C.如图所示的位移——时间图像是让底片沿x轴方向以一定速度匀速运动得到的
D.图像中振子的疏密显示出振子位置变化的快慢
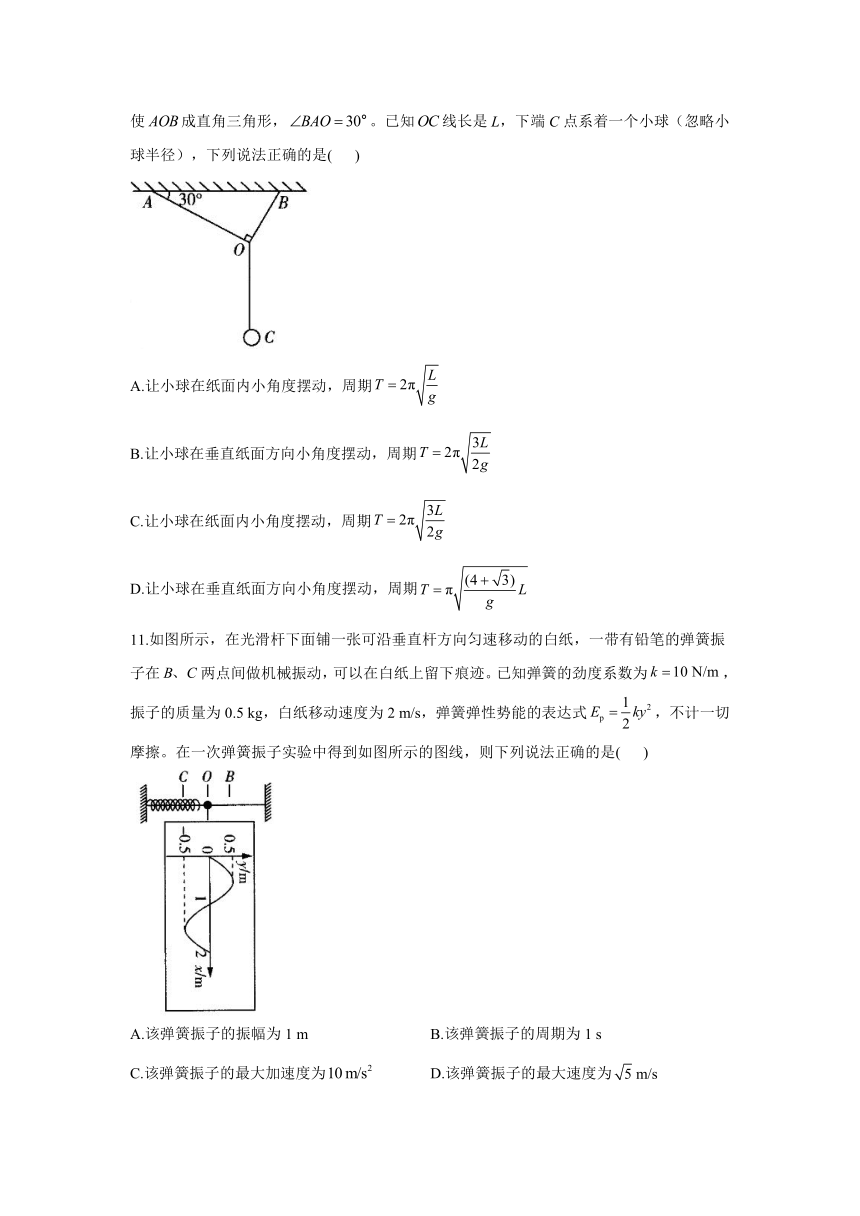
10.如图所示,三根细线于O点处打结,两端固定在同一水平面上相距为L的两点上,使成直角三角形,。已知线长是L,下端C点系着一个小球(忽略小球半径),下列说法正确的是( )
A.让小球在纸面内小角度摆动,周期
B.让小球在垂直纸面方向小角度摆动,周期
C.让小球在纸面内小角度摆动,周期
D.让小球在垂直纸面方向小角度摆动,周期
11.如图所示,在光滑杆下面铺一张可沿垂直杆方向匀速移动的白纸,一带有铅笔的弹簧振子在两点间做机械振动,可以在白纸上留下痕迹。已知弹簧的劲度系数为,振子的质量为0.5 kg,白纸移动速度为2 m/s,弹簧弹性势能的表达式,不计一切摩擦。在一次弹簧振子实验中得到如图所示的图线,则下列说法正确的是( )
A.该弹簧振子的振幅为1 m B.该弹簧振子的周期为1 s
C.该弹簧振子的最大加速度为 D.该弹簧振子的最大速度为
12.一钩码和一轻弹簧组成弹簧振子,如图甲所示的装置可用于研究该弹簧振子的受迫振动。匀速转动把手时,曲杆给弹簧振子驱动力,使振子做受迫振动,把手匀速转动的周期就是驱动力的周期,改变把手匀速转动的速度就可以改变驱动力的周期。若保持把手不动,给钩码一向下的初速度,钩码便做简谐运动,振动图线如图乙所示。当把手以某一速度匀速转动,受迫振动稳定时,钩码的振动图线如图丙所示。若用表示弹簧振子的固有频率,f表示驱动力的频率,则( )
A.由图线可知
B.由图线可知
C.由图线可知钩码做受迫振动的周期为8 s
D.由图线可知,缓慢增大把手转动速度至15 r/min,稳定后钩码振动的振幅也将增大
13.一个质点做简谐运动的图像如图所示,下列说法正确的是( )
A.质点振动频率为4 Hz
B.在10 s内质点经过的路程是20 cm
C.在5 s末,质点的速度为零,加速度最大
D.和两时刻,质点的位移大小相等,都是
E.质点的速度v随时间t的变化规律为
14.如图所示,一轻质弹簧上端系于天花板上,下端挂一质量为m的小球,弹簧的劲度系数为k,用手托住小球使弹簧处于原长,放手后,小球做简谐运动,则下列说法正确的是( )
A.小球做简谐运动的最大回复力为
B.从放手到小球运动到最低点,下降的高度为
C.小球运动到最低点时的加速度大小为
D.小球运动到平衡位置时的动能为
15.某实验小组利用如图甲所示的装置测定当地的重力加速度。
(1)为了使测量误差尽量小,下列说法中正确的是________;
A.组装单摆须选用密度和直径都较小的摆球
B.组装单摆须选用轻且不易伸长的细线
C.实验时须使摆球在同一竖直面内摆动
D.为了使单摆的周期大一些,应使摆线相距平衡位置有较大的角度
(2)该实验小组用20分度的游标卡尺测量小球的直径,某次测量的示数如图乙所示,则小球直径_______cm;
(3)某同学用米尺测出悬线的长度为L,让小球在竖直平面内摆动。当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数为1、2、3…。当数到40时,停止计时,测得时间为t。改变悬线长度,多次测量,利用计算机作出了图线如图丙所示。根据图丙可以得出当地的重力加速度______。(取,结果保留三位有效数字)
答案以及解析
1.答案:D
解析:本题易错之处在于不理解简谐运动中各物理量之间的关系。若t时刻和时刻振子相对平衡位置的位移大小相等,方向相同,说明质点经过同一位置,但时间差不一定为T的整数倍,A错误;速度大小相等方向相反,说明质点经过同一位置或关于平衡位置对称的位置,故不一定等于的整数倍,B错误;距离平衡位置越近速度越大,可知时两时刻位移大小之和不一定等于振幅,只有从平衡位置开始运动,或从最大位移处开始运动,两时刻位移大小之和才等于振幅,C错误;若,两个时刻一定关于平衡位置对称,速度大小一定相等,方向一定相反,D正确。
2.答案:C
解析:由于振幅A为20 cm,振动方程为(从平衡位置开始计时,),由于高度差不超过10 cm,游客能舒服地登船,代入数据可知,在一个振动周期内,临界时刻为,所以在一个周期内登船舒服的时间为,故选C。
3.答案:A
解析:本题的易错之处是误将木块与小车之间的静摩擦力当作两者组成系统的最大回复力。小车做简谐运动的回复力是木块对它的静摩擦力,当它们的位移最大时,加速度最大,受到的静摩擦力最大,为了不发生相对滑动,小车的最大加速度,即系统振动的最大加速度。对整体:达到最大位移时的加速度最大,回复力,则最大振幅。
故选A。
4.答案:B
解析:单摆摆动时的周期为,摆球在地球表面受到的万有引力等于重力,即,得,因此,选项B正确,选项ACD错误。
5.答案:A
解析:当驱动力的频率与振动系统的固有频率相同时,振幅最大,所以固有频率约为3Hz,选项A正确,B错误;受迫振动的振动周期由驱动力的周期决定,所以圆盘匀速转动的周期增大,系统的振动频率减小,选项C错误;系统的固有频率不变, 共振曲线的峰值位置不变,选项D错误。
6.答案:C
解析:由题图乙可知,该振动的振幅为,周期,所以,结合振动图像可知,该振动方程为。时,振子的位移,故A错误;由题图乙可知,和时,振子的位移大小不同,所以速度的大小一定不相等,故B错误;和时,振子的位移大小不同,所以加速度的大小一定不相同,故C错误;由题图乙可知,到时间内,振子的位移为正,正在逐渐増大,所以系统的势能逐渐增加,故D正确。
7.答案:B
解析:从单摆的位移时间图像可以看出两个单摆的周期相等,根据周期公式可知,两个单摆的摆长相等,周期与摆球的质量无关,故A错误,B正确;从题图可以看出,时刻,甲到达了正向最大位移处而乙才开始从平衡位置向正向的最大位移处运动,所以两单摆相位差为,C错误;由于两个摆的初相位不同,若经过的时间不是四分之一周期的整数倍,则不满足,故D错误。
8.答案:D
解析:振动过程中木块A与弹簧组成的系统机械能守恒,木块A机械能不守恒,故A错误;当弹簧处于伸长至最长状态时,M刚好对地面压力为零,故弹簧中弹力,此时A有最大加速度,由,得,由对称性,当A运动至最低点时,弹簧中弹力大小为,但此时弹簧是处于压缩状态,根据牛顿第二定律得,即,所以木块B对地面的最大压力,振幅为最大位移与平衡位置的距离,则振幅为,故D正确,BC错误。
9.答案:ABD
解析:题中图像的坐标原点是建立在弹簧振子合力为零的位置,振子在振动过程中是沿x轴方向振动的,故AB正确;频闪照相是在相同时间内留下的振子的像,让底片垂直x轴方向以适当的速度匀速运动,便可得到题中位移——时间图像,因此振子的疏密显示了它的位置变化的快慢,故C错误,D正确。
10.答案:AD
解析:本题的易错之处是摆长的确定。当小球在纸面内做小角度的摆动时,圆心是O点,摆长为L,故周期为,故A正确,C错误;当小球在垂直纸面方向做小角度摆动时,圆心在所在的水平面上且在O点正上方,摆长为,故周期为,故B错误,D正确。
11.答案:BCD
解析:弹簧振子的振幅为振子偏离平衡位置的最大距离,所以该弹簧振子的振幅为,选项A错误;由题图所示振子振动曲线可知,白纸移动,振动一个周期,所以弹簧振子的周期为,选项B正确;该弹簧振子所受最大回复力,最大加速度为,选项C正确;根据题述弹簧弹性势能的表达式为,弹簧振子振动过程中机械能守恒,由可得该弹簧振子的最大速度为,选项D正确。
12.答案:CD
解析:由题图乙可知弹簧振子的固有周期为4 s,因此弹簧振子的固有频率,由题图丙可知弹簧振子做受迫振动的周期为8 s,受迫振动的频率,故AB错误,C正确;当转速时,驱动力频率为,受迫振动的频率和弹簧振子的固有频率相同,达到共振,因此振幅增大,故D正确。
13.答案:BCD
解析:由题图可知周期为,则频率为,故A错误。质点在一个周期内通过的路程是4个振幅,,则在10 s内质点经过的路程是,故B正确。在5 s末,质点位于正向最大位移处,速度为零,加速度最大,故C正确。因质点的位移随时间变化规律为,则质点的速度v随时间t的变化规律为,故E错误。将和分别代入位移随时间变化的关系式中可得,两时刻质点的位移大小相等,都是,故D正确。
14.答案:ABD
解析:刚放手时,弹簧处于原长,在小球做简谐运动的最大位移处,此时小球只受重力,回复力大小为,A正确;小球在平衡位置时,弹簧伸长量设为x,根据胡克定律可知,解得,所以小球的振幅,根据简谐运动的对称性可知,最低点在平衡位置下方x处,故下降最大高度为,B正确;小球运动到最低点时受到的弹力,根据牛顿第二定律有,代入数据得,C错误;小球从初始位置到经过平衡位置的过程,根据机械能守恒有,解得,D正确。
15.答案:(1)BC
(2)0.810
(3)9.80
解析:本题考查利用单摆测定重力加速度。
(1)组装单摆须选用密度较大且直径较小的摆球,选项A错误;组装单摆须选用轻且不易伸长的细线,选项B正确;实验时须使摆球在同一竖直面内摆动,选项C正确;单摆的摆角不得超过5°,否则单摆的运动就不能视为简谐运动,选项D错误。
(2)小球直径。
(3)单摆的周期为,由单摆周期公式可得,则有,由题图丙可知斜率,解得。
机械振动(B)卷
1.一弹簧振子做简谐运动,周期为T,下列说法正确的是( )
A.若t时刻和时刻振子相对平衡位置的位移大小相等,方向相同,则一定等于T的整数倍
B.若t时刻和时刻振子运动速度大小相等,方向相反,则一定等于的整数倍
C.若,则t和两时刻,振子的位移大小之和一定等于振幅
D.若,则在t时刻和时刻振子速度的大小一定相等
2.一位游客在千岛湖边欲乘坐游船,当日风浪较大,游船上下浮动。可把游船浮动简化成竖直方向的简谐运动,振幅为20 cm,周期为3.0 s。当船上升到最高点时,甲板刚好与码头地面平齐。地面与甲板的高度差不超过10 cm时,游客能舒服地登船。在一个周期内,游客能舒服登船的时间是( )
A.0.5 s B.0.75 s C.1.0 s D.1.5 s
3.如图,一个质量为m的木块放在质量为M的平板小车上,它们之间的最大静摩擦力是,在劲度系数为k的轻质弹簧作用下,沿光滑水平面做简谐运动,为使小车能跟木块一起振动,不发生相对滑动,则简谐运动的振幅不能大于( )
A. B. C. D.
4.在科学研究中,科学家常将未知现象同已知现象进行比较,找出其共同点,进一步推测未知现象的特性和规律。法国物理学家库仑在研究异种电荷的吸引力问题时,曾将扭秤的振动周期与电荷间距离的关系类比单摆的振动周期与摆球到地心距离的关系。已知单摆摆长为,引力常量为G,地球质量为M,摆球到地心的距离为r,则单摆振动周期T与距离r的关系式为( )
A. B. C. D.
5.如图甲所示,竖直圆盘转动时,可带动固定在圆盘上的T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球,共同组成 —个振动系统。当圆盘静止时,小球可稳定振动。现使圆盘以4s的周期匀速转动,经过一段时间后,小球振动达到稳定。改变圆盘匀速转动的周期,系统的共振曲线(振幅A与驱动力的频率f的关系)如图乙所示,则(?? )
A.此振动系统的固有频率约为3Hz
B.此振动系统的固有频率约为0.25Hz
C.若圆盘匀速转动的周期增大,系统的振动频率不变
D.若圆盘匀速转动的周期增大,共振曲线的峰值将向右移动
6.如图甲所示,弹簧振子以点O为平衡位置,在两点之间做简谐运动。取向右为正方向,振子的位移x随时间t的变化如图乙所示,下列说法正确的是( )
A.时,振子在O点左侧10 cm处
B.和时,振子的速度相同
C.和时,振子的加速度相同
D.从到,系统的势能逐渐增加
7.下图为同一实验中甲、乙两个单摆的振动图像,从图像可知( )
A.两摆球质量相等 B.两单摆的摆长相等
C.两单摆相位相差π D.在相同的时间内,两摆球通过的路程总有
8.两木块质量分别为,用劲度系数为k的轻弹簧连在一起,放在水平地面上,如图所示,用外力将木块A压下一段距离,木块A静止,释放后A上下做简谐运动。在振动过程中,木块B刚好始终不离开地面(即它对地面最小压力为零)。以下说法正确的是( )
A.在振动过程中木块A的机械能守恒 B.A做简谐运动的振幅为
C.A做简谐运动的振幅为 D.木块B对地面的最大压力是
9.如图所示是用频闪照相的方法获得的弹簧振子的位移——时间图像,下列有关该图像的说法正确的是( )
A.该图像的坐标原点是建立在弹簧振子合力为零的位置
B.从图像可以看出振子在振动过程中是沿x轴方向振动的
C.如图所示的位移——时间图像是让底片沿x轴方向以一定速度匀速运动得到的
D.图像中振子的疏密显示出振子位置变化的快慢
10.如图所示,三根细线于O点处打结,两端固定在同一水平面上相距为L的两点上,使成直角三角形,。已知线长是L,下端C点系着一个小球(忽略小球半径),下列说法正确的是( )
A.让小球在纸面内小角度摆动,周期
B.让小球在垂直纸面方向小角度摆动,周期
C.让小球在纸面内小角度摆动,周期
D.让小球在垂直纸面方向小角度摆动,周期
11.如图所示,在光滑杆下面铺一张可沿垂直杆方向匀速移动的白纸,一带有铅笔的弹簧振子在两点间做机械振动,可以在白纸上留下痕迹。已知弹簧的劲度系数为,振子的质量为0.5 kg,白纸移动速度为2 m/s,弹簧弹性势能的表达式,不计一切摩擦。在一次弹簧振子实验中得到如图所示的图线,则下列说法正确的是( )
A.该弹簧振子的振幅为1 m B.该弹簧振子的周期为1 s
C.该弹簧振子的最大加速度为 D.该弹簧振子的最大速度为
12.一钩码和一轻弹簧组成弹簧振子,如图甲所示的装置可用于研究该弹簧振子的受迫振动。匀速转动把手时,曲杆给弹簧振子驱动力,使振子做受迫振动,把手匀速转动的周期就是驱动力的周期,改变把手匀速转动的速度就可以改变驱动力的周期。若保持把手不动,给钩码一向下的初速度,钩码便做简谐运动,振动图线如图乙所示。当把手以某一速度匀速转动,受迫振动稳定时,钩码的振动图线如图丙所示。若用表示弹簧振子的固有频率,f表示驱动力的频率,则( )
A.由图线可知
B.由图线可知
C.由图线可知钩码做受迫振动的周期为8 s
D.由图线可知,缓慢增大把手转动速度至15 r/min,稳定后钩码振动的振幅也将增大
13.一个质点做简谐运动的图像如图所示,下列说法正确的是( )
A.质点振动频率为4 Hz
B.在10 s内质点经过的路程是20 cm
C.在5 s末,质点的速度为零,加速度最大
D.和两时刻,质点的位移大小相等,都是
E.质点的速度v随时间t的变化规律为
14.如图所示,一轻质弹簧上端系于天花板上,下端挂一质量为m的小球,弹簧的劲度系数为k,用手托住小球使弹簧处于原长,放手后,小球做简谐运动,则下列说法正确的是( )
A.小球做简谐运动的最大回复力为
B.从放手到小球运动到最低点,下降的高度为
C.小球运动到最低点时的加速度大小为
D.小球运动到平衡位置时的动能为
15.某实验小组利用如图甲所示的装置测定当地的重力加速度。
(1)为了使测量误差尽量小,下列说法中正确的是________;
A.组装单摆须选用密度和直径都较小的摆球
B.组装单摆须选用轻且不易伸长的细线
C.实验时须使摆球在同一竖直面内摆动
D.为了使单摆的周期大一些,应使摆线相距平衡位置有较大的角度
(2)该实验小组用20分度的游标卡尺测量小球的直径,某次测量的示数如图乙所示,则小球直径_______cm;
(3)某同学用米尺测出悬线的长度为L,让小球在竖直平面内摆动。当小球经过最低点时开始计时,并计数为0,此后小球每经过最低点一次,依次计数为1、2、3…。当数到40时,停止计时,测得时间为t。改变悬线长度,多次测量,利用计算机作出了图线如图丙所示。根据图丙可以得出当地的重力加速度______。(取,结果保留三位有效数字)
答案以及解析
1.答案:D
解析:本题易错之处在于不理解简谐运动中各物理量之间的关系。若t时刻和时刻振子相对平衡位置的位移大小相等,方向相同,说明质点经过同一位置,但时间差不一定为T的整数倍,A错误;速度大小相等方向相反,说明质点经过同一位置或关于平衡位置对称的位置,故不一定等于的整数倍,B错误;距离平衡位置越近速度越大,可知时两时刻位移大小之和不一定等于振幅,只有从平衡位置开始运动,或从最大位移处开始运动,两时刻位移大小之和才等于振幅,C错误;若,两个时刻一定关于平衡位置对称,速度大小一定相等,方向一定相反,D正确。
2.答案:C
解析:由于振幅A为20 cm,振动方程为(从平衡位置开始计时,),由于高度差不超过10 cm,游客能舒服地登船,代入数据可知,在一个振动周期内,临界时刻为,所以在一个周期内登船舒服的时间为,故选C。
3.答案:A
解析:本题的易错之处是误将木块与小车之间的静摩擦力当作两者组成系统的最大回复力。小车做简谐运动的回复力是木块对它的静摩擦力,当它们的位移最大时,加速度最大,受到的静摩擦力最大,为了不发生相对滑动,小车的最大加速度,即系统振动的最大加速度。对整体:达到最大位移时的加速度最大,回复力,则最大振幅。
故选A。
4.答案:B
解析:单摆摆动时的周期为,摆球在地球表面受到的万有引力等于重力,即,得,因此,选项B正确,选项ACD错误。
5.答案:A
解析:当驱动力的频率与振动系统的固有频率相同时,振幅最大,所以固有频率约为3Hz,选项A正确,B错误;受迫振动的振动周期由驱动力的周期决定,所以圆盘匀速转动的周期增大,系统的振动频率减小,选项C错误;系统的固有频率不变, 共振曲线的峰值位置不变,选项D错误。
6.答案:C
解析:由题图乙可知,该振动的振幅为,周期,所以,结合振动图像可知,该振动方程为。时,振子的位移,故A错误;由题图乙可知,和时,振子的位移大小不同,所以速度的大小一定不相等,故B错误;和时,振子的位移大小不同,所以加速度的大小一定不相同,故C错误;由题图乙可知,到时间内,振子的位移为正,正在逐渐増大,所以系统的势能逐渐增加,故D正确。
7.答案:B
解析:从单摆的位移时间图像可以看出两个单摆的周期相等,根据周期公式可知,两个单摆的摆长相等,周期与摆球的质量无关,故A错误,B正确;从题图可以看出,时刻,甲到达了正向最大位移处而乙才开始从平衡位置向正向的最大位移处运动,所以两单摆相位差为,C错误;由于两个摆的初相位不同,若经过的时间不是四分之一周期的整数倍,则不满足,故D错误。
8.答案:D
解析:振动过程中木块A与弹簧组成的系统机械能守恒,木块A机械能不守恒,故A错误;当弹簧处于伸长至最长状态时,M刚好对地面压力为零,故弹簧中弹力,此时A有最大加速度,由,得,由对称性,当A运动至最低点时,弹簧中弹力大小为,但此时弹簧是处于压缩状态,根据牛顿第二定律得,即,所以木块B对地面的最大压力,振幅为最大位移与平衡位置的距离,则振幅为,故D正确,BC错误。
9.答案:ABD
解析:题中图像的坐标原点是建立在弹簧振子合力为零的位置,振子在振动过程中是沿x轴方向振动的,故AB正确;频闪照相是在相同时间内留下的振子的像,让底片垂直x轴方向以适当的速度匀速运动,便可得到题中位移——时间图像,因此振子的疏密显示了它的位置变化的快慢,故C错误,D正确。
10.答案:AD
解析:本题的易错之处是摆长的确定。当小球在纸面内做小角度的摆动时,圆心是O点,摆长为L,故周期为,故A正确,C错误;当小球在垂直纸面方向做小角度摆动时,圆心在所在的水平面上且在O点正上方,摆长为,故周期为,故B错误,D正确。
11.答案:BCD
解析:弹簧振子的振幅为振子偏离平衡位置的最大距离,所以该弹簧振子的振幅为,选项A错误;由题图所示振子振动曲线可知,白纸移动,振动一个周期,所以弹簧振子的周期为,选项B正确;该弹簧振子所受最大回复力,最大加速度为,选项C正确;根据题述弹簧弹性势能的表达式为,弹簧振子振动过程中机械能守恒,由可得该弹簧振子的最大速度为,选项D正确。
12.答案:CD
解析:由题图乙可知弹簧振子的固有周期为4 s,因此弹簧振子的固有频率,由题图丙可知弹簧振子做受迫振动的周期为8 s,受迫振动的频率,故AB错误,C正确;当转速时,驱动力频率为,受迫振动的频率和弹簧振子的固有频率相同,达到共振,因此振幅增大,故D正确。
13.答案:BCD
解析:由题图可知周期为,则频率为,故A错误。质点在一个周期内通过的路程是4个振幅,,则在10 s内质点经过的路程是,故B正确。在5 s末,质点位于正向最大位移处,速度为零,加速度最大,故C正确。因质点的位移随时间变化规律为,则质点的速度v随时间t的变化规律为,故E错误。将和分别代入位移随时间变化的关系式中可得,两时刻质点的位移大小相等,都是,故D正确。
14.答案:ABD
解析:刚放手时,弹簧处于原长,在小球做简谐运动的最大位移处,此时小球只受重力,回复力大小为,A正确;小球在平衡位置时,弹簧伸长量设为x,根据胡克定律可知,解得,所以小球的振幅,根据简谐运动的对称性可知,最低点在平衡位置下方x处,故下降最大高度为,B正确;小球运动到最低点时受到的弹力,根据牛顿第二定律有,代入数据得,C错误;小球从初始位置到经过平衡位置的过程,根据机械能守恒有,解得,D正确。
15.答案:(1)BC
(2)0.810
(3)9.80
解析:本题考查利用单摆测定重力加速度。
(1)组装单摆须选用密度较大且直径较小的摆球,选项A错误;组装单摆须选用轻且不易伸长的细线,选项B正确;实验时须使摆球在同一竖直面内摆动,选项C正确;单摆的摆角不得超过5°,否则单摆的运动就不能视为简谐运动,选项D错误。
(2)小球直径。
(3)单摆的周期为,由单摆周期公式可得,则有,由题图丙可知斜率,解得。
