2020-2021学年苏科版七年级数学下册平面图形的认识二复习课件(共28张PPT)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册平面图形的认识二复习课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 11:59:23 | ||
图片预览



文档简介
(共28张PPT)
平面图形的认识二
平行的性质及判定
图形的平移
三角形的三边关系
三角形的中线,垂线,角平分线
目录
多边形的内角和,外角和
01
02
03
04
05
同一平面内,两条直线的关系有相交,平行。
在同一平面内,不相交的两条直线叫做平行;两条线段、线段与射线平行指他们所在的直线平行。
平行线的性质
经过直线外一点,有且只有一条直线与已知直线平行。
如果两条直线与第三条直线平行,那么这两条直线平行。
补充:如果两条直线都和第三条直线垂直,那么这两条直线也平行。
平行的定义和性质
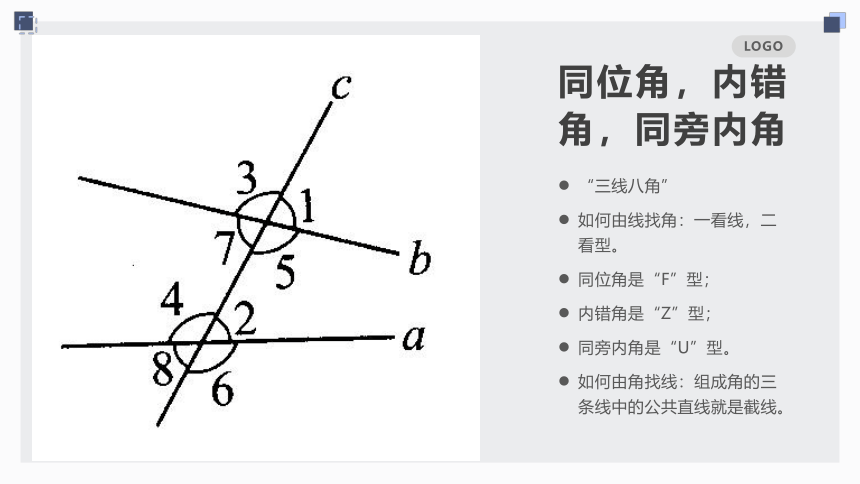
“三线八角”
如何由线找角:一看线,二看型。
同位角是“F”型;
内错角是“Z”型;
同旁内角是“U”型。
如何由角找线:组成角的三条线中的公共直线就是截线。
同位角,内错角,同旁内角
LOGO
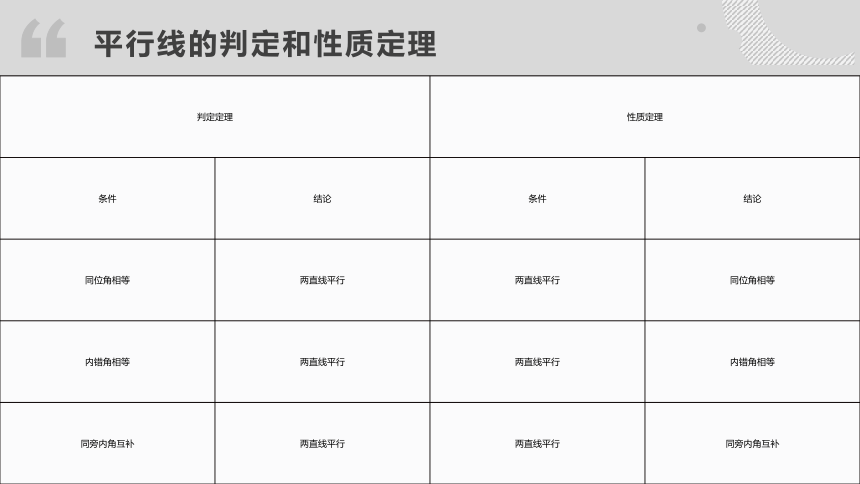
平行线的判定和性质定理
判定定理
性质定理
条件
结论
条件
结论
同位角相等
两直线平行
两直线平行
同位角相等
内错角相等
两直线平行
两直线平行
内错角相等
同旁内角互补
两直线平行
两直线平行
同旁内角互补
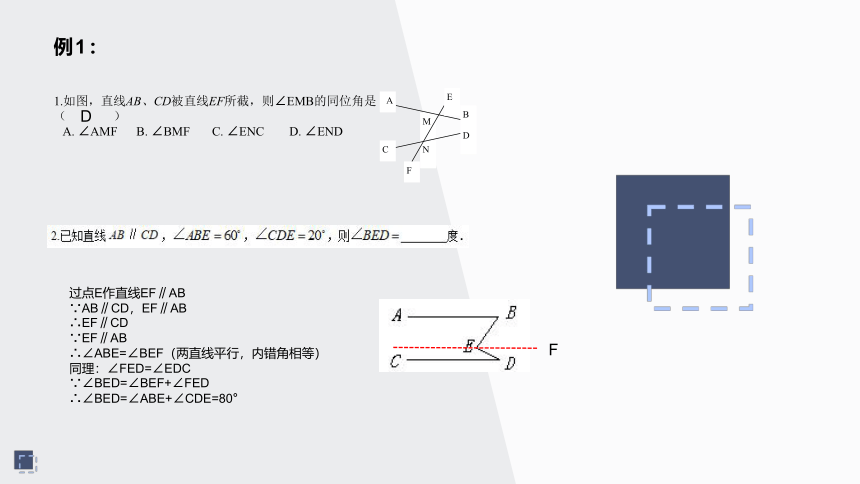
例1:
1.如图,直线AB、CD被直线EF所截,则∠EMB的同位角是(
)
A.
∠AMF
B.
∠BMF
C.
∠ENC
D.
∠END
M
B
D
N
F
C
A
E
D
F
过点E作直线EF∥AB
∵AB∥CD,EF∥AB
∴EF∥CD
∵EF∥AB
∴∠ABE=∠BEF(两直线平行,内错角相等)
同理:∠FED=∠EDC
∵∠BED=∠BEF+∠FED
∴∠BED=∠ABE+∠CDE=80°
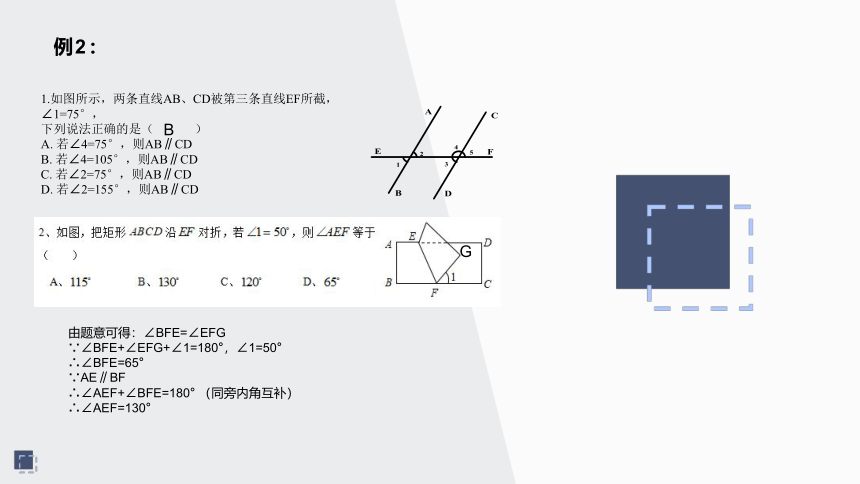
例2:
1.如图所示,两条直线AB、CD被第三条直线EF所截,∠1=75°,
下列说法正确的是(
)
A.
若∠4=75°,则AB∥CD
B.
若∠4=105°,则AB∥CD
C.
若∠2=75°,则AB∥CD
D.
若∠2=155°,则AB∥CD
B
由题意可得:∠BFE=∠EFG
∵∠BFE+∠EFG+∠1=180°,∠1=50°
∴∠BFE=65°
∵AE∥BF
∴∠AEF+∠BFE=180°
(同旁内角互补)
∴∠AEF=130°
G
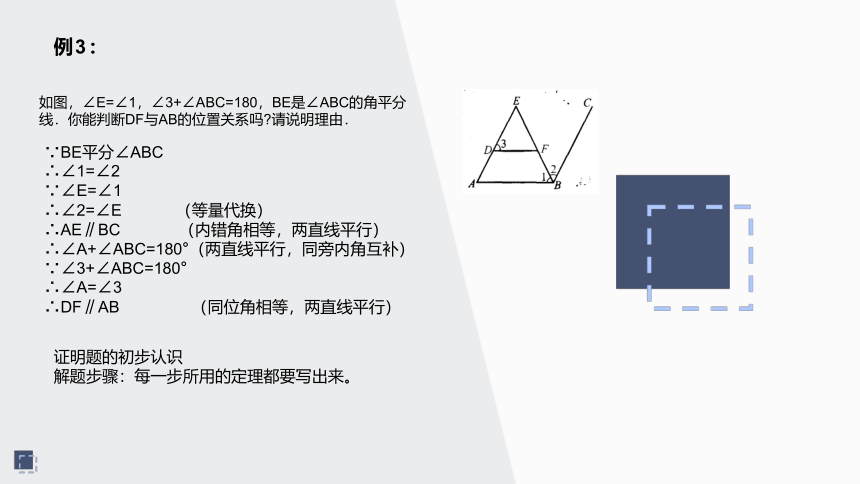
例3:
如图,∠E=∠1,∠3+∠ABC=180,BE是∠ABC的角平分
线.你能判断DF与AB的位置关系吗?请说明理由.
∵BE平分∠ABC
∴∠1=∠2
∵∠E=∠1
∴∠2=∠E
(等量代换)
∴AE∥BC
(内错角相等,两直线平行)
∴∠A+∠ABC=180°(两直线平行,同旁内角互补)
∵∠3+∠ABC=180°
∴∠A=∠3
∴DF∥AB
(同位角相等,两直线平行)
证明题的初步认识
解题步骤:每一步所用的定理都要写出来。
例4:
∵∠1+∠2=180°,∠1+∠EFD=180°
∴∠2=∠EFD
∴AB∥EF
(内错角相等,两直线平行)
∴∠DEF=∠BDE
(两直线平行,内错角相等)
∵∠DEF=∠A
∴∠BDE=∠A
(等量代换)
∴DE∥AC
(同位角相等,两直线平行)
∴∠DEB=∠ACB
(两直线平行,同位角相等)
例5:
图形平移的性质
平移不改变图形的形状和大小
平移前后对应点连线平行且相等
对应线段和角相等
例1:
如图,将边长为4个单位的等边△ABC沿边BC向右
平移2个单位得到△DEF,则四边形ABFD的周长为
根据平移的基本性质:AD=BE=CF=2
∴EC=4-2=2
∴BF=6
∴四边形ABFD周长为2+4+4+6=16
例2:
如图所示时2个重叠的直角三角形,将其中一个三角形沿BC方向平移得到△DEF,如果AB=8cm,BE=4cm,DH=3cm,那么阴影部分面积是多少?
阴影部分面积=梯形ABEH的面积
HE=8-3=5cm
(8+5)×4÷2=26cm2
三角形的任意两边之和大于第三边;三角形的任意两边之差小于第三边。
若三角形的三边分别为a、b、c,则︱a-b︳<c<a+b
三角形三边之间的关系:
例1:
设a,b,c是?ABC的三边,化简
例2:
(1)等边三角形
(2)等腰三角形
例3:
D
延长BP交AC于D
▲ABD中,AB+AD>PB+PD
▲PCD中,PD+CD>PC
AB+AD+PD+CD>PB+PD+PC
AB+AC>PB+PC
▲OAB中,OA+OB>AB
▲OAD中,OA+OD>AD
▲OCD中,OC+OD>CD
▲OBC中,OB+OC>BC
(OA+OB+OC+OD)×2>(AB+AD+CD+BC)
AC+BD>1/2(AB+AD+CD+BC)
例4:
三角形中,从一个顶点向它的对边所在的直线作垂线,顶点与垂足之间的线段叫做三角形的高。(垂心)
三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。(内心)
三角形中,连线一个顶点与它对边中点的线段,叫做三角形的中线。(重心)
三角形重要线段
三角形的重要线段
三角形的三条中线交与三角形内一点,且三角形的任意一条中线把这个三角形分成面积相等的两个三角形。
三角形的三条角平分线交与三角形内一点。
锐角三角形的三条高交与三角形内一点;直角三角形的三条高交与直角顶点;钝角三角形的三条高交与三角形外一点。
拓展
例1:
5平方厘米。
例2:
∠A=180°-35°-85°=60°
∠BAD=30°
∠ADE=35°+30°=65°
∠E=90°-65°=25°
∵AD平分∠BAC
∴:∠BAD=∠CAD=
∠BAC
∵∠B=α,∠ACB=β
∴∠BAC=180°-α-β
∴∠BAD=
(180°-α-β)
∴∠ADE=α+
(180°-α-β)
=90°+
α-
β
∵PE⊥AD
∴∠E=90°-∠ADE
=
多边形内角和,外角和
?
3
?
1
?
2
三角形内角和180°,外角和360°。∠A的外角=∠B+∠C
多边形内角和=180°·(n-2)
多边形外角和360°
例1:
18:
2,2
19:
∠FEC=∠A+∠B
∠C=180°-∠FEC-∠EFC
∵∠EFC=∠DFB
∴∠C=180°-58°-44°-42°=36°
20:
∠1+∠2+∠3=360°-90°-60°-108°=102°
∠1+∠2=102°-32°=70°
例2:
直角△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点。令∠PDA=∠1,
∠PEB=∠2,
∠DPE=∠α
(1)如图1,若点P在线段AB上,且∠α=50°,则∠1+
∠2=
(2)如图2,若点P在边AB上运动,则∠α、∠1、∠2之间的关系为
四边形CDPE内角和为360°
∠C+∠α+∠CDP+∠CEP=360°
90°+50°+180°-∠1+180°-∠2=360°
∠1+∠2=140°
∠1+∠2=90°+∠α
例3:
G
解:过点O作直线OG∥CE
∵OG∥CE
∴∠GOC=∠OCE=180°-∠ACE
∵OG∥CE,CE∥DF
∴OG∥DF
∴∠ODF+∠DOG=180°
∴∠DOG=180°-∠ODF
∵∠AOB=∠GOC+∠GOD
∴∠AOB=180°-∠ACE+180°-∠ODF=360°-(∠ACE+∠ODF)
∴∠AOB+∠ACE+∠ODF=360°
∠P=360°-∠PCO-∠AOB-∠ODP
=360°-90°-β-(360°-α-β)÷2
=270°-β-180°+
α+
β
=90°+
α-
β
例4:
如图1所示,△ABO与△CDO称为“对顶三角形”,其中∠A+∠B=∠C+∠D.利用这个结论,在图2中,∠A+∠B+∠C+∠D+∠E+∠F+∠G=
°.
解:如图2,连接BE,
由对顶三角形可得,∠C+∠D=∠CBE+∠DEB,
∵五边形ABEFG中,∠A+∠ABE+∠BEF+∠F+∠G=540°,
即∠A+∠ABC+∠CBE+∠BED+∠DEF+∠F+∠G=540°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F+∠G=540°,
故答案为:540°.
平面图形的认识二
平行的性质及判定
图形的平移
三角形的三边关系
三角形的中线,垂线,角平分线
目录
多边形的内角和,外角和
01
02
03
04
05
同一平面内,两条直线的关系有相交,平行。
在同一平面内,不相交的两条直线叫做平行;两条线段、线段与射线平行指他们所在的直线平行。
平行线的性质
经过直线外一点,有且只有一条直线与已知直线平行。
如果两条直线与第三条直线平行,那么这两条直线平行。
补充:如果两条直线都和第三条直线垂直,那么这两条直线也平行。
平行的定义和性质
“三线八角”
如何由线找角:一看线,二看型。
同位角是“F”型;
内错角是“Z”型;
同旁内角是“U”型。
如何由角找线:组成角的三条线中的公共直线就是截线。
同位角,内错角,同旁内角
LOGO
平行线的判定和性质定理
判定定理
性质定理
条件
结论
条件
结论
同位角相等
两直线平行
两直线平行
同位角相等
内错角相等
两直线平行
两直线平行
内错角相等
同旁内角互补
两直线平行
两直线平行
同旁内角互补
例1:
1.如图,直线AB、CD被直线EF所截,则∠EMB的同位角是(
)
A.
∠AMF
B.
∠BMF
C.
∠ENC
D.
∠END
M
B
D
N
F
C
A
E
D
F
过点E作直线EF∥AB
∵AB∥CD,EF∥AB
∴EF∥CD
∵EF∥AB
∴∠ABE=∠BEF(两直线平行,内错角相等)
同理:∠FED=∠EDC
∵∠BED=∠BEF+∠FED
∴∠BED=∠ABE+∠CDE=80°
例2:
1.如图所示,两条直线AB、CD被第三条直线EF所截,∠1=75°,
下列说法正确的是(
)
A.
若∠4=75°,则AB∥CD
B.
若∠4=105°,则AB∥CD
C.
若∠2=75°,则AB∥CD
D.
若∠2=155°,则AB∥CD
B
由题意可得:∠BFE=∠EFG
∵∠BFE+∠EFG+∠1=180°,∠1=50°
∴∠BFE=65°
∵AE∥BF
∴∠AEF+∠BFE=180°
(同旁内角互补)
∴∠AEF=130°
G
例3:
如图,∠E=∠1,∠3+∠ABC=180,BE是∠ABC的角平分
线.你能判断DF与AB的位置关系吗?请说明理由.
∵BE平分∠ABC
∴∠1=∠2
∵∠E=∠1
∴∠2=∠E
(等量代换)
∴AE∥BC
(内错角相等,两直线平行)
∴∠A+∠ABC=180°(两直线平行,同旁内角互补)
∵∠3+∠ABC=180°
∴∠A=∠3
∴DF∥AB
(同位角相等,两直线平行)
证明题的初步认识
解题步骤:每一步所用的定理都要写出来。
例4:
∵∠1+∠2=180°,∠1+∠EFD=180°
∴∠2=∠EFD
∴AB∥EF
(内错角相等,两直线平行)
∴∠DEF=∠BDE
(两直线平行,内错角相等)
∵∠DEF=∠A
∴∠BDE=∠A
(等量代换)
∴DE∥AC
(同位角相等,两直线平行)
∴∠DEB=∠ACB
(两直线平行,同位角相等)
例5:
图形平移的性质
平移不改变图形的形状和大小
平移前后对应点连线平行且相等
对应线段和角相等
例1:
如图,将边长为4个单位的等边△ABC沿边BC向右
平移2个单位得到△DEF,则四边形ABFD的周长为
根据平移的基本性质:AD=BE=CF=2
∴EC=4-2=2
∴BF=6
∴四边形ABFD周长为2+4+4+6=16
例2:
如图所示时2个重叠的直角三角形,将其中一个三角形沿BC方向平移得到△DEF,如果AB=8cm,BE=4cm,DH=3cm,那么阴影部分面积是多少?
阴影部分面积=梯形ABEH的面积
HE=8-3=5cm
(8+5)×4÷2=26cm2
三角形的任意两边之和大于第三边;三角形的任意两边之差小于第三边。
若三角形的三边分别为a、b、c,则︱a-b︳<c<a+b
三角形三边之间的关系:
例1:
设a,b,c是?ABC的三边,化简
例2:
(1)等边三角形
(2)等腰三角形
例3:
D
延长BP交AC于D
▲ABD中,AB+AD>PB+PD
▲PCD中,PD+CD>PC
AB+AD+PD+CD>PB+PD+PC
AB+AC>PB+PC
▲OAB中,OA+OB>AB
▲OAD中,OA+OD>AD
▲OCD中,OC+OD>CD
▲OBC中,OB+OC>BC
(OA+OB+OC+OD)×2>(AB+AD+CD+BC)
AC+BD>1/2(AB+AD+CD+BC)
例4:
三角形中,从一个顶点向它的对边所在的直线作垂线,顶点与垂足之间的线段叫做三角形的高。(垂心)
三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。(内心)
三角形中,连线一个顶点与它对边中点的线段,叫做三角形的中线。(重心)
三角形重要线段
三角形的重要线段
三角形的三条中线交与三角形内一点,且三角形的任意一条中线把这个三角形分成面积相等的两个三角形。
三角形的三条角平分线交与三角形内一点。
锐角三角形的三条高交与三角形内一点;直角三角形的三条高交与直角顶点;钝角三角形的三条高交与三角形外一点。
拓展
例1:
5平方厘米。
例2:
∠A=180°-35°-85°=60°
∠BAD=30°
∠ADE=35°+30°=65°
∠E=90°-65°=25°
∵AD平分∠BAC
∴:∠BAD=∠CAD=
∠BAC
∵∠B=α,∠ACB=β
∴∠BAC=180°-α-β
∴∠BAD=
(180°-α-β)
∴∠ADE=α+
(180°-α-β)
=90°+
α-
β
∵PE⊥AD
∴∠E=90°-∠ADE
=
多边形内角和,外角和
?
3
?
1
?
2
三角形内角和180°,外角和360°。∠A的外角=∠B+∠C
多边形内角和=180°·(n-2)
多边形外角和360°
例1:
18:
2,2
19:
∠FEC=∠A+∠B
∠C=180°-∠FEC-∠EFC
∵∠EFC=∠DFB
∴∠C=180°-58°-44°-42°=36°
20:
∠1+∠2+∠3=360°-90°-60°-108°=102°
∠1+∠2=102°-32°=70°
例2:
直角△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点。令∠PDA=∠1,
∠PEB=∠2,
∠DPE=∠α
(1)如图1,若点P在线段AB上,且∠α=50°,则∠1+
∠2=
(2)如图2,若点P在边AB上运动,则∠α、∠1、∠2之间的关系为
四边形CDPE内角和为360°
∠C+∠α+∠CDP+∠CEP=360°
90°+50°+180°-∠1+180°-∠2=360°
∠1+∠2=140°
∠1+∠2=90°+∠α
例3:
G
解:过点O作直线OG∥CE
∵OG∥CE
∴∠GOC=∠OCE=180°-∠ACE
∵OG∥CE,CE∥DF
∴OG∥DF
∴∠ODF+∠DOG=180°
∴∠DOG=180°-∠ODF
∵∠AOB=∠GOC+∠GOD
∴∠AOB=180°-∠ACE+180°-∠ODF=360°-(∠ACE+∠ODF)
∴∠AOB+∠ACE+∠ODF=360°
∠P=360°-∠PCO-∠AOB-∠ODP
=360°-90°-β-(360°-α-β)÷2
=270°-β-180°+
α+
β
=90°+
α-
β
例4:
如图1所示,△ABO与△CDO称为“对顶三角形”,其中∠A+∠B=∠C+∠D.利用这个结论,在图2中,∠A+∠B+∠C+∠D+∠E+∠F+∠G=
°.
解:如图2,连接BE,
由对顶三角形可得,∠C+∠D=∠CBE+∠DEB,
∵五边形ABEFG中,∠A+∠ABE+∠BEF+∠F+∠G=540°,
即∠A+∠ABC+∠CBE+∠BED+∠DEF+∠F+∠G=540°,
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F+∠G=540°,
故答案为:540°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
