2020-2021学年高一数学人教A版必修二第一章1.2.2 空间几何体的三视图教学设计
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修二第一章1.2.2 空间几何体的三视图教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 09:40:43 | ||
图片预览

文档简介
空间几何体的三视图
一、教学目标
⒈知识与技能:使学生学会画三视图、体会三视图的作用,能由三视图想象几何体,从而进行几何体与其三视图之间的相互转化。
⒉过程与方法:通过直观感知,操作确认,提高学生的空间想象能力、几何直观能力,培养学生的应用意识。
⒊情感、态度与价值观:感受数学就在身边,提高学生的学习立体几何的兴趣,培养学生大胆创新、勇于探索、互相合作的精神,并形成良好的思维习惯。
二学情分析
在初中,学生对正方体、长方体、圆柱、圆锥、球等都有了直观认识;会画直棱柱、圆柱、圆锥与球的三视图,会判断简单物体的三视图,能根据展开图描述基本几何体或实物原型。能够利用基本几何体与其三视图、展开图之间的关系解决现实生活中的简单问题。但对三视图与几何体之间的量关系还不清楚,对三视图的具体画法还处于模糊的感知阶段。
三重点难点
1.重点:
(1)画出空间几何体及简单组合体的三视图,
(2)给出三视图,还原或想象出原实际图的结构特征,体会三视图的作用。
2.难点:识别三视图所表示的空间几何体。
四教学过程
(一)创设情境,导入新课
情境1:“横看成岭侧成峰,远近高低各不同.”这说明从不同的角度看同一物体视觉的效果可能不同,要比较真实反映出物体,必须从多角度观看物体;
情境二:正视,侧视和俯视图片展示.
这堂课我们来学习从不同角度看空间几何体,即空间几何体的三视图。
(二)结合情境,给出定义
1、从几何体的前面向后面正投影,得到的投影图称为几何体的正视图(主视图)。
2、从几何体的左面向右面正投影,得到的投影图称为几何体的侧视图(左视图)。
3、从几何体的上面向下面正投影,得到的投影图称为几何体的俯视图。
几何体的正视图、侧视图和俯视图统称为几何体的三视图。
(三)结合例题,讲解新知
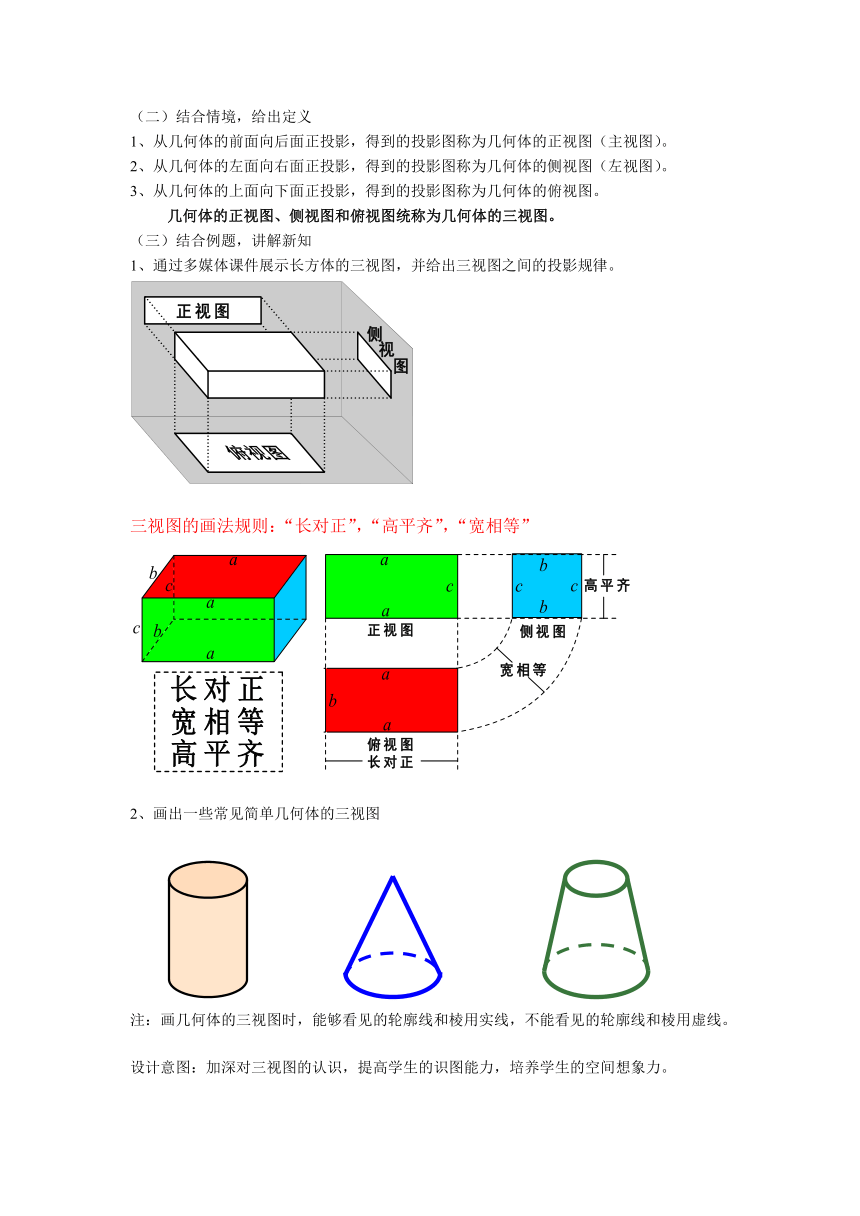
1、通过多媒体课件展示长方体的三视图,并给出三视图之间的投影规律。
三视图的画法规则:“长对正”,“高平齐”,“宽相等”
2、画出一些常见简单几何体的三视图
注:画几何体的三视图时,能够看见的轮廓线和棱用实线,不能看见的轮廓线和棱用虚线。
设计意图:加深对三视图的认识,提高学生的识图能力,培养学生的空间想象力。
(四)典例分析,突破难点
(1)画出直三棱柱的三视图
正视图 侧视图
俯视图
注意:1. 侧视图为原图中的红色矩形
2.侧视图中矩形的宽恰是俯视图中三角形的底边上的高
练习:请您画出六棱柱的三视图
小结:怎样画三视图
(1)分别从几何体的正前方、正左方、正上方观察分析。
(2)侧视图在主视图右边,俯视图在主视图下边。
(3)按照“长对正、高平齐、宽相等”作出对应的三视图。它是指:正视图和俯视图一样长:正视图和侧视图一样高:俯视图和侧视图一样宽。
(4)作图时,能看见的轮廓线和棱用实线表示,不能看见的用虚线表示。
(3)三视图与几何体之间的相互转化。
(五)课堂练习,学以致用
1.下图是五个相同的小正方体搭成的几何体,其左视图是( )
(2)下面是空心圆柱在指定方向上的视图,正确的是( )
(3)一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的高和底面边长分别为( )
如图,下列四个几何体中,其主视图、左视图、俯视图中只有两个相同的是( )
(六) 布置作业:
课后习题,复习本节内容并预习下一节内容
一、教学目标
⒈知识与技能:使学生学会画三视图、体会三视图的作用,能由三视图想象几何体,从而进行几何体与其三视图之间的相互转化。
⒉过程与方法:通过直观感知,操作确认,提高学生的空间想象能力、几何直观能力,培养学生的应用意识。
⒊情感、态度与价值观:感受数学就在身边,提高学生的学习立体几何的兴趣,培养学生大胆创新、勇于探索、互相合作的精神,并形成良好的思维习惯。
二学情分析
在初中,学生对正方体、长方体、圆柱、圆锥、球等都有了直观认识;会画直棱柱、圆柱、圆锥与球的三视图,会判断简单物体的三视图,能根据展开图描述基本几何体或实物原型。能够利用基本几何体与其三视图、展开图之间的关系解决现实生活中的简单问题。但对三视图与几何体之间的量关系还不清楚,对三视图的具体画法还处于模糊的感知阶段。
三重点难点
1.重点:
(1)画出空间几何体及简单组合体的三视图,
(2)给出三视图,还原或想象出原实际图的结构特征,体会三视图的作用。
2.难点:识别三视图所表示的空间几何体。
四教学过程
(一)创设情境,导入新课
情境1:“横看成岭侧成峰,远近高低各不同.”这说明从不同的角度看同一物体视觉的效果可能不同,要比较真实反映出物体,必须从多角度观看物体;
情境二:正视,侧视和俯视图片展示.
这堂课我们来学习从不同角度看空间几何体,即空间几何体的三视图。
(二)结合情境,给出定义
1、从几何体的前面向后面正投影,得到的投影图称为几何体的正视图(主视图)。
2、从几何体的左面向右面正投影,得到的投影图称为几何体的侧视图(左视图)。
3、从几何体的上面向下面正投影,得到的投影图称为几何体的俯视图。
几何体的正视图、侧视图和俯视图统称为几何体的三视图。
(三)结合例题,讲解新知
1、通过多媒体课件展示长方体的三视图,并给出三视图之间的投影规律。
三视图的画法规则:“长对正”,“高平齐”,“宽相等”
2、画出一些常见简单几何体的三视图
注:画几何体的三视图时,能够看见的轮廓线和棱用实线,不能看见的轮廓线和棱用虚线。
设计意图:加深对三视图的认识,提高学生的识图能力,培养学生的空间想象力。
(四)典例分析,突破难点
(1)画出直三棱柱的三视图
正视图 侧视图
俯视图
注意:1. 侧视图为原图中的红色矩形
2.侧视图中矩形的宽恰是俯视图中三角形的底边上的高
练习:请您画出六棱柱的三视图
小结:怎样画三视图
(1)分别从几何体的正前方、正左方、正上方观察分析。
(2)侧视图在主视图右边,俯视图在主视图下边。
(3)按照“长对正、高平齐、宽相等”作出对应的三视图。它是指:正视图和俯视图一样长:正视图和侧视图一样高:俯视图和侧视图一样宽。
(4)作图时,能看见的轮廓线和棱用实线表示,不能看见的用虚线表示。
(3)三视图与几何体之间的相互转化。
(五)课堂练习,学以致用
1.下图是五个相同的小正方体搭成的几何体,其左视图是( )
(2)下面是空心圆柱在指定方向上的视图,正确的是( )
(3)一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的高和底面边长分别为( )
如图,下列四个几何体中,其主视图、左视图、俯视图中只有两个相同的是( )
(六) 布置作业:
课后习题,复习本节内容并预习下一节内容
