2020-2021学年人教版数学八年级下册18.2.3正方形-课件(共26张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册18.2.3正方形-课件(共26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
18.2.3
正方形
第十八章
平行四边形
平行四边形再认识
1.掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系与区别.
学习目标
活动一:
请同学们拿出手中的
矩形图片,快速的折出一个大正方形,你是怎么做的?和大家分享一下。
思考:1、在矩形变成正方形的过程中,长和宽哪个量发生了变化?
2、你能根据刚才的活动给出正方形的定义吗?
一
探究新知
探究小结
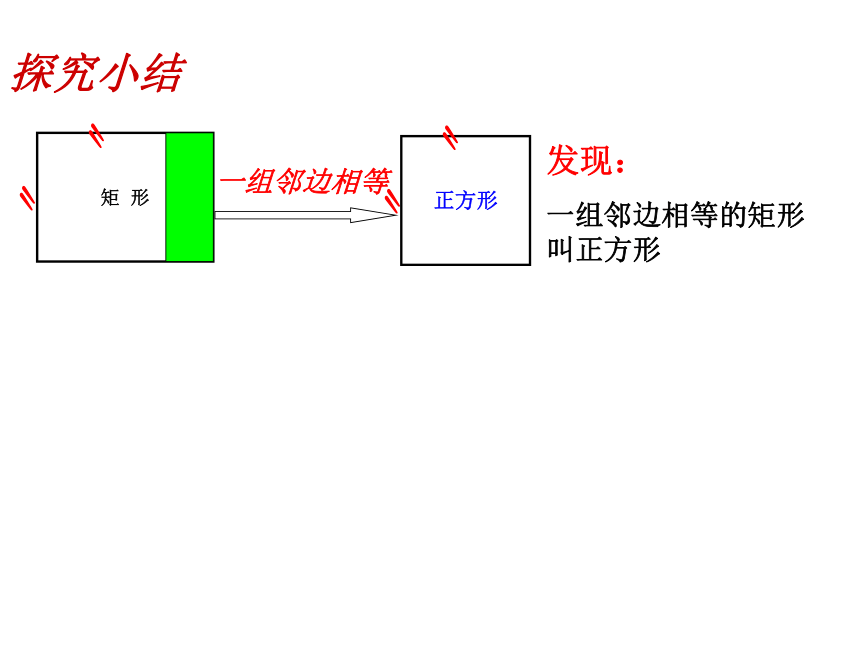
矩
形
〃
〃
正方形
一组邻边相等
〃
〃
发现:
一组邻边相等的矩形叫正方形
活动二:
请同学们观察老师手中的菱形框架,它是如何变成正方形的?
思考:1、在菱形变成正方形的过程中,哪个量发生了变化?
2、你能根据刚才的活动给出正方形的定义吗?
一
探究新知
探究小结
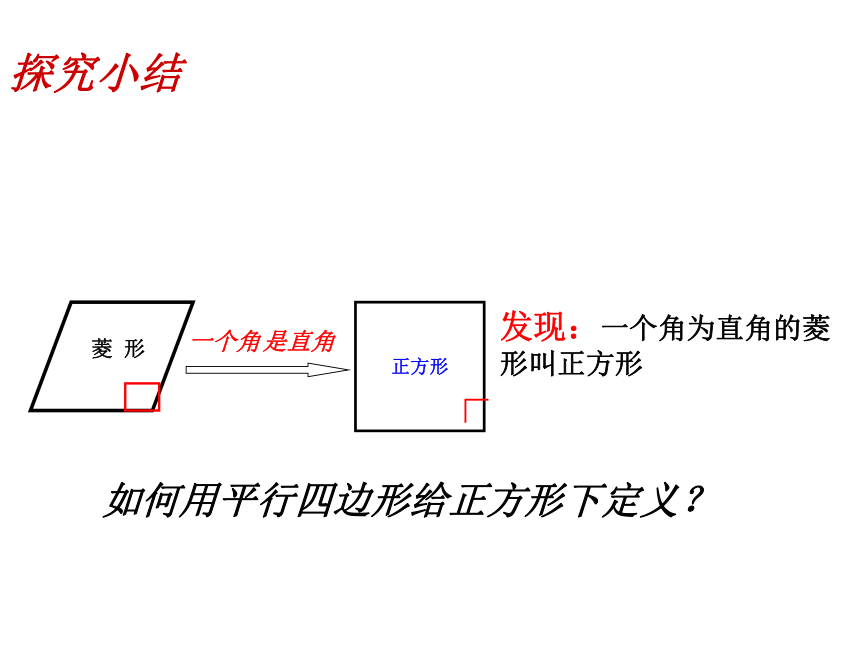
菱
形
一个角
是直角
正方形
∟
发现:一个角为直角的菱形叫正方形
如何用平行四边形给正方形下定义?
⑴有一组邻边相等的平行四边形(菱形)
⑵有一个角是直角的平行四边形(矩形)
两层含义
正方形
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形
形成概念
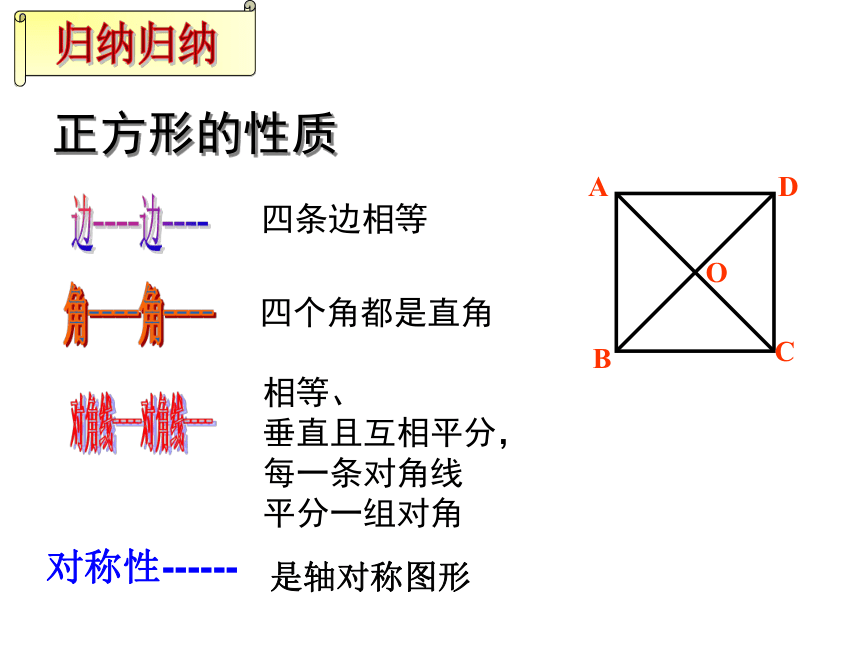
正方形的性质
四条边相等
四个角都是直角
相等、
垂直且互相平分,
每一条对角线
平分一组对角
A
B
C
D
O
边----
角----
对角线----
对称性------
是轴对称图形
归纳
正方形是轴对称图形,有几条对称轴,它的对称轴是什么?
快速抢答
正方形具有而矩形不一定具有的性质是(
)
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.
2.正方形具有而菱形不一定具有的性(
)
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
选一选
例题解析
O
A
B
C
D
求证:正方形的两条对角线把
这个正方形分成四个全等的等腰直
角三角形。
第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明
学一学
求证:△ABO、△BCO、△CDO、
△DAO是全等的等腰直角三角形.
△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
A
B
C
D
O
已知:如图,四边形ABCD是正
方形,对角线AC、BD相交于点O,
证明:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、
(1)判定一个平行四边形是正方形,
还应具备什么条件?
(2)判定一个矩形是正方形,
还应具备什么条件?
(3)判定一个菱形是正方形,
还应具备什么条件?
二
合作交流(一)
平行四边形
正方形
1、
2、
正方形
菱形
一角是直角
一组邻边相等
矩形
3、
正方形
正方形的判定方法:
(可从平行四边形、矩形、菱形为基础)
对角线互相垂直
一组邻边相等
且一角为直角
对角线垂直且相等
对角线相等
平行四边形
矩形
菱形
正方形
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形
之间的包含关系
想一想
√
√
√
×
(1)对角线互相垂直且相等的四边形是正方形(
)
(2)如果一个菱形的对角线相等,那么它一定
是正方形
(
)
(3)如果一个矩形的对角线互相垂直,那么它
一定是正方形
(
)
(4)四条边相等,且有一个角是直角的四边形
是正方形(
)
(5)四个角都相等的四边形是正方形
(
)
(6)四条边都相等的四边形是正方形
(
)
判断题:
×
×
快速反应
已知:正方形ABCD中,点E、F、G
、H分别是AB
、BC
、CD
、DA的中点,试判断四边形EFGH是正方形吗?为什么?
1
2
3
证明:∵
四边形ABCD是正方形∴∠A=∠
B=
∠
C=∠D=90°,
AB=AD=DC=BC
(正方形的四条边都相等四个角都是直角).
∵
点E、F、G、H分别是AB、BC、CD、DA的中点
∴AE=BE=BF=CF=CG=DG=DH=AH
∴
△AEH、△BFE、
△CGF
、
△DHG都是等腰直角三角形且全等.
∴EF=FG=HG=EH
∵
∠BFE=∠CFG=
45°
∴
∠EFG=90
°
∴
四边形EFGH是正方形(有一个角是直角的菱形是正方形).
A
B
C
D
E
F
G
H
二
合作交流(二)
已知:正方形ABCD中,点E、F、G
、H分别在AB
、BC
、CD
、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?
A
B
C
D
E
F
G
H
1
2
3
证明:∵
四边形ABCD是正方形
∴
∠A=
∠
B=
∠
C=∠D=90°,AB=AD=DC=BC
又∵
AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴
△AEH≌△BFE≌
△CGF
≌
△DHG.
∴EH=HG=FG=EF
∵
∠1=∠3.∠3+∠2=90°
∴∠1+∠2=90°
∴
∠EFG=90
°
∴
四边形EFGH是正方形
二
合作交流(二)
变一变
用心学习,有所收获
我理解了……
我学会了……
……
我知道了……
A
B
C
D
1菱形、矩形、正方形都具有的性质(
)
A对角线相等且互相平分
B对角线相等且互相垂直平分
C对角线互相平分
D四条边相等,四个角相等
达标检测
2.正方形ABCD的面积是9cm2。则AB=________AC=___________
3cm
C
3
在直角三角形ABC中,CD平分直角∠ACB交AB于D,DE⊥AC,DF⊥BC。求证:四边形CEDF是正方形。
A
B
C
D
E
F
∴四边形CEDF是正方形(
)
∴
DE=DF(
)
DE⊥AC,
DF⊥BC
∵
CD平分∠ACB
∴
四边形CEDF为矩形(
)
∵∠ACB=90°
∴
∠DEC=90°,
∠DFC=90°
证明:∵
DE⊥AC,DF⊥BC
有三个角是直角的四边形是矩形
角平分线的定理
有一组邻边相等的矩形是正方形
拓展提高:如图B、C、E是同一直线上的三个点,四边形ABCD与CEFG是正方形,连接BG、DE
(1)观察、猜想BG与DE之间的大小关系,并说明理由。
(2)正方形CEFG在绕点C旋转过程中,BG与DE之间的关系是否仍然成立。
A
B
C
E
F
D
G
A
D
B
G
F
E
C
作业
习题18.2第13、15题
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是矩形又是菱形的四边形是正方形。
1
、定义法:
2、矩形菱形法:
3、对角线法:
两条对角线互相垂直平分且相等的四边形是正方形。
你能总结出正方形有哪些判定方法吗?
诲人不倦
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,
去发现,去总结。
教师寄语
再见
下课了!
18.2.3
正方形
第十八章
平行四边形
平行四边形再认识
1.掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系与区别.
学习目标
活动一:
请同学们拿出手中的
矩形图片,快速的折出一个大正方形,你是怎么做的?和大家分享一下。
思考:1、在矩形变成正方形的过程中,长和宽哪个量发生了变化?
2、你能根据刚才的活动给出正方形的定义吗?
一
探究新知
探究小结
矩
形
〃
〃
正方形
一组邻边相等
〃
〃
发现:
一组邻边相等的矩形叫正方形
活动二:
请同学们观察老师手中的菱形框架,它是如何变成正方形的?
思考:1、在菱形变成正方形的过程中,哪个量发生了变化?
2、你能根据刚才的活动给出正方形的定义吗?
一
探究新知
探究小结
菱
形
一个角
是直角
正方形
∟
发现:一个角为直角的菱形叫正方形
如何用平行四边形给正方形下定义?
⑴有一组邻边相等的平行四边形(菱形)
⑵有一个角是直角的平行四边形(矩形)
两层含义
正方形
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形
形成概念
正方形的性质
四条边相等
四个角都是直角
相等、
垂直且互相平分,
每一条对角线
平分一组对角
A
B
C
D
O
边----
角----
对角线----
对称性------
是轴对称图形
归纳
正方形是轴对称图形,有几条对称轴,它的对称轴是什么?
快速抢答
正方形具有而矩形不一定具有的性质是(
)
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.
2.正方形具有而菱形不一定具有的性(
)
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
选一选
例题解析
O
A
B
C
D
求证:正方形的两条对角线把
这个正方形分成四个全等的等腰直
角三角形。
第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明
学一学
求证:△ABO、△BCO、△CDO、
△DAO是全等的等腰直角三角形.
△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.
A
B
C
D
O
已知:如图,四边形ABCD是正
方形,对角线AC、BD相交于点O,
证明:
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、
(1)判定一个平行四边形是正方形,
还应具备什么条件?
(2)判定一个矩形是正方形,
还应具备什么条件?
(3)判定一个菱形是正方形,
还应具备什么条件?
二
合作交流(一)
平行四边形
正方形
1、
2、
正方形
菱形
一角是直角
一组邻边相等
矩形
3、
正方形
正方形的判定方法:
(可从平行四边形、矩形、菱形为基础)
对角线互相垂直
一组邻边相等
且一角为直角
对角线垂直且相等
对角线相等
平行四边形
矩形
菱形
正方形
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形
之间的包含关系
想一想
√
√
√
×
(1)对角线互相垂直且相等的四边形是正方形(
)
(2)如果一个菱形的对角线相等,那么它一定
是正方形
(
)
(3)如果一个矩形的对角线互相垂直,那么它
一定是正方形
(
)
(4)四条边相等,且有一个角是直角的四边形
是正方形(
)
(5)四个角都相等的四边形是正方形
(
)
(6)四条边都相等的四边形是正方形
(
)
判断题:
×
×
快速反应
已知:正方形ABCD中,点E、F、G
、H分别是AB
、BC
、CD
、DA的中点,试判断四边形EFGH是正方形吗?为什么?
1
2
3
证明:∵
四边形ABCD是正方形∴∠A=∠
B=
∠
C=∠D=90°,
AB=AD=DC=BC
(正方形的四条边都相等四个角都是直角).
∵
点E、F、G、H分别是AB、BC、CD、DA的中点
∴AE=BE=BF=CF=CG=DG=DH=AH
∴
△AEH、△BFE、
△CGF
、
△DHG都是等腰直角三角形且全等.
∴EF=FG=HG=EH
∵
∠BFE=∠CFG=
45°
∴
∠EFG=90
°
∴
四边形EFGH是正方形(有一个角是直角的菱形是正方形).
A
B
C
D
E
F
G
H
二
合作交流(二)
已知:正方形ABCD中,点E、F、G
、H分别在AB
、BC
、CD
、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?
A
B
C
D
E
F
G
H
1
2
3
证明:∵
四边形ABCD是正方形
∴
∠A=
∠
B=
∠
C=∠D=90°,AB=AD=DC=BC
又∵
AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴
△AEH≌△BFE≌
△CGF
≌
△DHG.
∴EH=HG=FG=EF
∵
∠1=∠3.∠3+∠2=90°
∴∠1+∠2=90°
∴
∠EFG=90
°
∴
四边形EFGH是正方形
二
合作交流(二)
变一变
用心学习,有所收获
我理解了……
我学会了……
……
我知道了……
A
B
C
D
1菱形、矩形、正方形都具有的性质(
)
A对角线相等且互相平分
B对角线相等且互相垂直平分
C对角线互相平分
D四条边相等,四个角相等
达标检测
2.正方形ABCD的面积是9cm2。则AB=________AC=___________
3cm
C
3
在直角三角形ABC中,CD平分直角∠ACB交AB于D,DE⊥AC,DF⊥BC。求证:四边形CEDF是正方形。
A
B
C
D
E
F
∴四边形CEDF是正方形(
)
∴
DE=DF(
)
DE⊥AC,
DF⊥BC
∵
CD平分∠ACB
∴
四边形CEDF为矩形(
)
∵∠ACB=90°
∴
∠DEC=90°,
∠DFC=90°
证明:∵
DE⊥AC,DF⊥BC
有三个角是直角的四边形是矩形
角平分线的定理
有一组邻边相等的矩形是正方形
拓展提高:如图B、C、E是同一直线上的三个点,四边形ABCD与CEFG是正方形,连接BG、DE
(1)观察、猜想BG与DE之间的大小关系,并说明理由。
(2)正方形CEFG在绕点C旋转过程中,BG与DE之间的关系是否仍然成立。
A
B
C
E
F
D
G
A
D
B
G
F
E
C
作业
习题18.2第13、15题
有一组邻边相等并且有一个角是直角的平行四边形是正方形。
既是矩形又是菱形的四边形是正方形。
1
、定义法:
2、矩形菱形法:
3、对角线法:
两条对角线互相垂直平分且相等的四边形是正方形。
你能总结出正方形有哪些判定方法吗?
诲人不倦
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,
去发现,去总结。
教师寄语
再见
下课了!
