2020—2021学年人教版数学七年级下册8.3实际问题与二元一次方程组课件(共17张)
文档属性
| 名称 | 2020—2021学年人教版数学七年级下册8.3实际问题与二元一次方程组课件(共17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 368.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
实际问题与二元一次方程组
——工程问题
工程问题:
工作量=
工作效率=
工作时间=
复习引入
用一元一次方程解决工程问题:
工程问题中常用的关系式有哪些?
工程问题
思考:一件工作,甲单独做20小
时完成,乙单独做12小时完成,
那么两人合作多少小时完成?
问:甲每小时完成全部工作的______;
乙每小时完成全部工作的_______;
甲、乙合作每小时完成全部工作的_______.
甲x小时完成全部工作的_______;
乙x小时完成全部工作的_______.
甲、乙合作x小时完成全部工作的
.
问:甲乙合作完成需要用32小时吗?
工作效率
工作时间
工作量
甲
乙
合作
20
12
1
1
比一比,赛一赛.
1.一项工作甲独做5天完成,乙独做10天完成,那么甲每天的工作效率是
,乙每天的工作效率
,两人合作3天完成的工作量
,此时剩余的工作量是
.
2.一项工作甲独做a天完成,乙独做b天完成,那么甲每天的工作效率是
,乙每天的工作效率是
,两人合作3天完成的工量
,此时剩余的工作量是
.
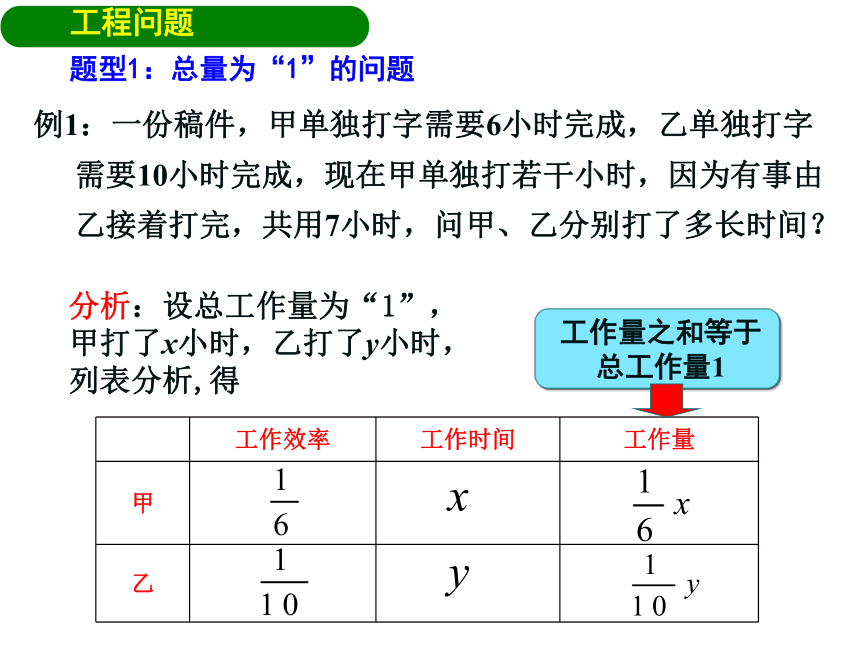
例1:一份稿件,甲单独打字需要6小时完成,乙单独打字需要10小时完成,现在甲单独打若干小时,因为有事由乙接着打完,共用7小时,问甲、乙分别打了多长时间?
工程问题
题型1:总量为“1”的问题
工作效率
工作时间
工作量
甲
乙
分析:设总工作量为“1”,
甲打了x小时,乙打了y小时,
列表分析,得
工作量之和等于总工作量1
工程问题
探究1:总量为“1”的问题
解:设总工作量为“1”,甲打了x小时,乙打了
y小时,根据题意,得
答:甲打了4.5小时,乙打了2.5小时.
工作效率
工作时间
工作量
甲
乙
工作量之和等于总工作量1
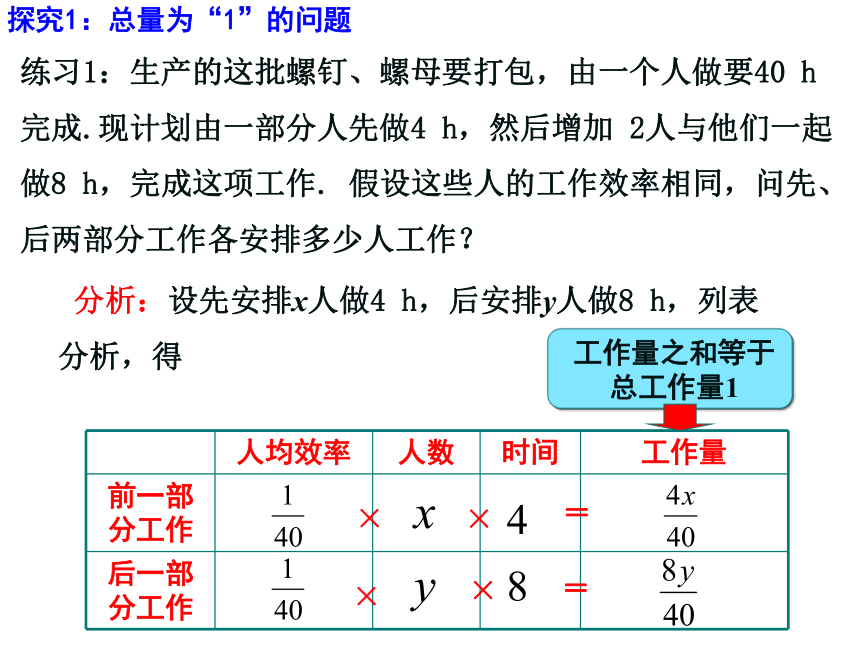
练习1:生产的这批螺钉、螺母要打包,由一个人做要40
h
完成.现计划由一部分人先做4
h,然后增加
2人与他们一起做8
h,完成这项工作.
假设这些人的工作效率相同,问先、后两部分工作各安排多少人工作?
人均效率
人数
时间
工作量
前一部分工作
后一部分工作
×
=
×
×
×
=
工作量之和等于总工作量1
探究1:总量为“1”的问题
分析:设先安排x人做4
h,后安排y人做8
h,列表分析,得
解:设先安排x人做4
h,后安排y人做8
h,根据题意,得
答:先安排2人,后安排4人.
探究1:总量为“1”的问题
人均效率
人数
时间
工作量
前一部分工作
后一部分工作
×
=
×
×
×
=
工作量之和等于总工作量1
例2.某工程队承包了一段全长1
957
m的隧道工程,甲、乙两个班组分别从南北两端同时掘进,已知甲组比乙组每天多掘进0.5
m,经过6天施工,甲、乙两组共掘进57
m.
求甲乙两班组平均每天各掘进多少米?
分析:设甲班组每天掘进
x
m,乙班组每天掘进
y
m.
列表分析,得
探究2:总量不为“1”的问题
工作效率
工作时间
工作量
甲
乙
工作量之和等于总工作量57
解:设甲班组每天掘进
x
m,乙班组每天掘进
y
m.根据题意,得
答:甲乙两班组平均每天各掘进5
m,4.5
m.
探究2:总量不为“1”的问题
工作效率
工作时间
工作量
甲
乙
工作量之和等于总工作量57
练习2:甲、乙两个工程队参与修建一条长600米的拦河大坝,若甲、乙两队一起修建12天可以完工,若甲队单独修建5天后乙队加入,两队再一起修建4天,刚好能够完成该工程的一半,求甲、乙两队每天各能修建多少米?
探究2:总量不为“1”的问题
分析:设甲队每天能修建x米,乙队每天能修建y米.
列表分析,得
工作效率
工作时间
工作量
甲
乙
合作
→
探究2:总量不为“1”的问题
解:设甲队每天能修建x米,乙队每天能修建y米.根据题意,得
答:甲队每天能修建20米,乙队每天能修建30米.
工作效率
工作时间
工作量
甲
乙
合作
→
练习3.小明家准备装修一套房子,若请甲、乙两个装修公司合作,则需6
周完成,需花费工钱5.2
万元;若先请甲公司单独做4
周后,剩下的请乙公司来做,则还需9
周才能完成,需花费工钱4.8
万元.求
(1)甲、乙公司每周的工作效率分别是多少.
(2)设请甲、乙公司工作一周需花费工钱分别为多少万元;
(3)只请一个公司单独完成,从节约开支的角度来考虑,小明家应该选甲公司还是乙公司?
巩固提高
分析:(1)甲公司每周的工作效率为x,乙公司每周的工作效率为y.列表分析得:
(2)设请甲公司工作一周需花费工钱a万元,请乙公司工作一周需花费工钱b万元,列表分析得:
工作效率
工作时间
工作量
甲
乙
合作
→
工作效率
工作时间
工作量
甲
乙
合作
→
解:(1)设总工作量为“1”,甲公司每周的工作效率为x,乙公司每周的工作效率为y.
根据题意,得
答:甲、乙公司每周的工作效率分别是
.
巩固提高
(2)设请甲公司工作一周需花费工钱a万元,请乙公司工作一周需花费工钱b万元,根据题意,得
答:请甲、乙公司工作一周需花费工钱分别为
万元、
万元.
(3)请甲公司单独完成需花费工钱:10×
=6(万元),
请乙公司单独完成需花费工钱:15×
=4(万元).
答:从节约开支的角度来考虑,小明家应该选乙公司.
小结
1、二元一次方程组在工程问题中的应用,工程问题主要分两类:①当题目中工作量未知时,通常用“1”表示总工作量,②工作量已知;
2、利用二元一次方程组解决工程问题时,注意几个步骤:审题(关键找等量关系),设未知数,列方程,解方程,验证,答。
作业
1、必做题:教材101页2,3题;
2、选做题:下面的思考题.
思考题:某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润可达4500元;经精加工后销售,每吨利润涨至7500元.当地一家农工商公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16t;如果进行精加工,每天可加工6t,但两种加式方式不能同时进行,受季节条件的限制,公司必须在15天之内将这批蔬菜全部销售或加工完毕,为此公司研制了三种加工方案.
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及加工的蔬菜在市场上全部销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好在15天完成,你认为选择哪种方案获利最多,为什么?
(拓展:若在加工过程中精加工损耗20%,粗加工损耗10%,其它条件不变,则选择哪种方案获利最多.)
实际问题与二元一次方程组
——工程问题
工程问题:
工作量=
工作效率=
工作时间=
复习引入
用一元一次方程解决工程问题:
工程问题中常用的关系式有哪些?
工程问题
思考:一件工作,甲单独做20小
时完成,乙单独做12小时完成,
那么两人合作多少小时完成?
问:甲每小时完成全部工作的______;
乙每小时完成全部工作的_______;
甲、乙合作每小时完成全部工作的_______.
甲x小时完成全部工作的_______;
乙x小时完成全部工作的_______.
甲、乙合作x小时完成全部工作的
.
问:甲乙合作完成需要用32小时吗?
工作效率
工作时间
工作量
甲
乙
合作
20
12
1
1
比一比,赛一赛.
1.一项工作甲独做5天完成,乙独做10天完成,那么甲每天的工作效率是
,乙每天的工作效率
,两人合作3天完成的工作量
,此时剩余的工作量是
.
2.一项工作甲独做a天完成,乙独做b天完成,那么甲每天的工作效率是
,乙每天的工作效率是
,两人合作3天完成的工量
,此时剩余的工作量是
.
例1:一份稿件,甲单独打字需要6小时完成,乙单独打字需要10小时完成,现在甲单独打若干小时,因为有事由乙接着打完,共用7小时,问甲、乙分别打了多长时间?
工程问题
题型1:总量为“1”的问题
工作效率
工作时间
工作量
甲
乙
分析:设总工作量为“1”,
甲打了x小时,乙打了y小时,
列表分析,得
工作量之和等于总工作量1
工程问题
探究1:总量为“1”的问题
解:设总工作量为“1”,甲打了x小时,乙打了
y小时,根据题意,得
答:甲打了4.5小时,乙打了2.5小时.
工作效率
工作时间
工作量
甲
乙
工作量之和等于总工作量1
练习1:生产的这批螺钉、螺母要打包,由一个人做要40
h
完成.现计划由一部分人先做4
h,然后增加
2人与他们一起做8
h,完成这项工作.
假设这些人的工作效率相同,问先、后两部分工作各安排多少人工作?
人均效率
人数
时间
工作量
前一部分工作
后一部分工作
×
=
×
×
×
=
工作量之和等于总工作量1
探究1:总量为“1”的问题
分析:设先安排x人做4
h,后安排y人做8
h,列表分析,得
解:设先安排x人做4
h,后安排y人做8
h,根据题意,得
答:先安排2人,后安排4人.
探究1:总量为“1”的问题
人均效率
人数
时间
工作量
前一部分工作
后一部分工作
×
=
×
×
×
=
工作量之和等于总工作量1
例2.某工程队承包了一段全长1
957
m的隧道工程,甲、乙两个班组分别从南北两端同时掘进,已知甲组比乙组每天多掘进0.5
m,经过6天施工,甲、乙两组共掘进57
m.
求甲乙两班组平均每天各掘进多少米?
分析:设甲班组每天掘进
x
m,乙班组每天掘进
y
m.
列表分析,得
探究2:总量不为“1”的问题
工作效率
工作时间
工作量
甲
乙
工作量之和等于总工作量57
解:设甲班组每天掘进
x
m,乙班组每天掘进
y
m.根据题意,得
答:甲乙两班组平均每天各掘进5
m,4.5
m.
探究2:总量不为“1”的问题
工作效率
工作时间
工作量
甲
乙
工作量之和等于总工作量57
练习2:甲、乙两个工程队参与修建一条长600米的拦河大坝,若甲、乙两队一起修建12天可以完工,若甲队单独修建5天后乙队加入,两队再一起修建4天,刚好能够完成该工程的一半,求甲、乙两队每天各能修建多少米?
探究2:总量不为“1”的问题
分析:设甲队每天能修建x米,乙队每天能修建y米.
列表分析,得
工作效率
工作时间
工作量
甲
乙
合作
→
探究2:总量不为“1”的问题
解:设甲队每天能修建x米,乙队每天能修建y米.根据题意,得
答:甲队每天能修建20米,乙队每天能修建30米.
工作效率
工作时间
工作量
甲
乙
合作
→
练习3.小明家准备装修一套房子,若请甲、乙两个装修公司合作,则需6
周完成,需花费工钱5.2
万元;若先请甲公司单独做4
周后,剩下的请乙公司来做,则还需9
周才能完成,需花费工钱4.8
万元.求
(1)甲、乙公司每周的工作效率分别是多少.
(2)设请甲、乙公司工作一周需花费工钱分别为多少万元;
(3)只请一个公司单独完成,从节约开支的角度来考虑,小明家应该选甲公司还是乙公司?
巩固提高
分析:(1)甲公司每周的工作效率为x,乙公司每周的工作效率为y.列表分析得:
(2)设请甲公司工作一周需花费工钱a万元,请乙公司工作一周需花费工钱b万元,列表分析得:
工作效率
工作时间
工作量
甲
乙
合作
→
工作效率
工作时间
工作量
甲
乙
合作
→
解:(1)设总工作量为“1”,甲公司每周的工作效率为x,乙公司每周的工作效率为y.
根据题意,得
答:甲、乙公司每周的工作效率分别是
.
巩固提高
(2)设请甲公司工作一周需花费工钱a万元,请乙公司工作一周需花费工钱b万元,根据题意,得
答:请甲、乙公司工作一周需花费工钱分别为
万元、
万元.
(3)请甲公司单独完成需花费工钱:10×
=6(万元),
请乙公司单独完成需花费工钱:15×
=4(万元).
答:从节约开支的角度来考虑,小明家应该选乙公司.
小结
1、二元一次方程组在工程问题中的应用,工程问题主要分两类:①当题目中工作量未知时,通常用“1”表示总工作量,②工作量已知;
2、利用二元一次方程组解决工程问题时,注意几个步骤:审题(关键找等量关系),设未知数,列方程,解方程,验证,答。
作业
1、必做题:教材101页2,3题;
2、选做题:下面的思考题.
思考题:某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润可达4500元;经精加工后销售,每吨利润涨至7500元.当地一家农工商公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16t;如果进行精加工,每天可加工6t,但两种加式方式不能同时进行,受季节条件的限制,公司必须在15天之内将这批蔬菜全部销售或加工完毕,为此公司研制了三种加工方案.
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及加工的蔬菜在市场上全部销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好在15天完成,你认为选择哪种方案获利最多,为什么?
(拓展:若在加工过程中精加工损耗20%,粗加工损耗10%,其它条件不变,则选择哪种方案获利最多.)
