2020-2021学年苏科版八年级下册第九章中心对称图形—平行四边形期中复习解答题精选(1)(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级下册第九章中心对称图形—平行四边形期中复习解答题精选(1)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 17:54:31 | ||
图片预览


文档简介
2021年八年级下册平行四边形期中复习解答题精选(1)
一、解答题
1.(2020·江苏无锡市·八年级期中)按要求作图,不要求写做法,但要保留作图痕迹.
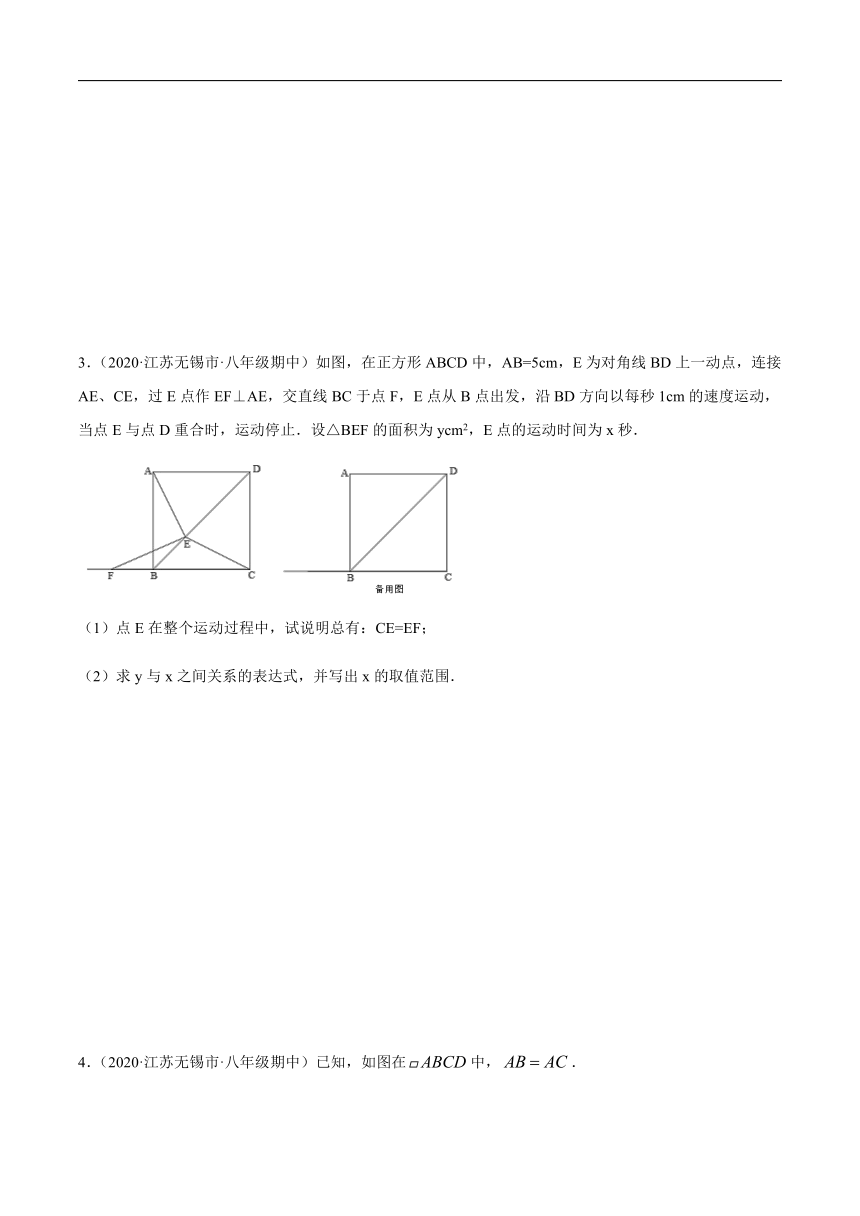
(1)如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.
(2)如图2,BE是菱形ABCD的边AD上的高,请只用直尺(不带刻度)作出菱形ABCD的边AB上的高DF.
2.(2020·江苏无锡市·八年级期中)在△ABC中,AB=12,AC=BC=10,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为D,点C的对应点为E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长.
在旋转过程中,过点D作DG垂直于直线AB,垂足为G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
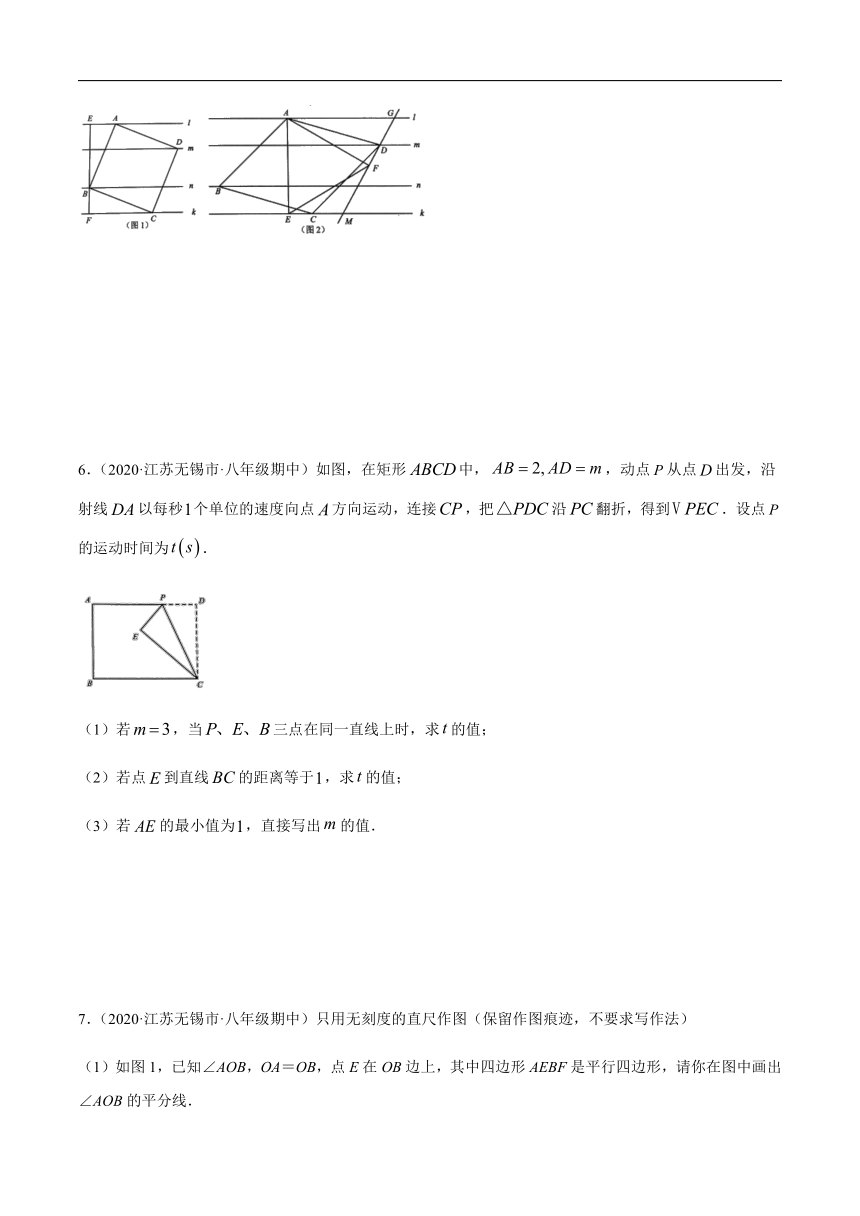
3.(2020·江苏无锡市·八年级期中)如图,在正方形ABCD中,AB=5cm,E为对角线BD上一动点,连接AE、CE,过E点作EF⊥AE,交直线BC于点F,E点从B点出发,沿BD方向以每秒1cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
(1)点E在整个运动过程中,试说明总有:CE=EF;
(2)求y与x之间关系的表达式,并写出x的取值范围.
4.(2020·江苏无锡市·八年级期中)已知,如图在中,.
(1)请用无刻度的直尺和圆规,画出中边上的中线;(作图要求:保留痕迹,不写作法.)
(2)请只用无刻度的直尺,画出中边上的高,并说明理由.
5.(2020·江苏无锡市·八年级期中)已知:平行线与与与之间的距离分别为且,.我们把四个顶点分别在这四条平行线上的四边形称为“线上四边形”
(1)如图1,正方形为“线上四边形”,于点的延长线交直线于点.求正方形的边长.
(2)如图2,菱形为“线上四边形”且是等边三角形,点在直线上,连接且的延长线分别交直线于点.求证:.
6.(2020·江苏无锡市·八年级期中)如图,在矩形中,,动点从点出发,沿射线以每秒个单位的速度向点方向运动,连接,把沿翻折,得到.设点的运动时间为.
(1)若,当三点在同一直线上时,求的值;
(2)若点到直线的距离等于,求的值;
(3)若的最小值为,直接写出的值.
7.(2020·江苏无锡市·八年级期中)只用无刻度的直尺作图(保留作图痕迹,不要求写作法)
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,其中四边形AEBF是平行四边形,请你在图中画出∠AOB的平分线.
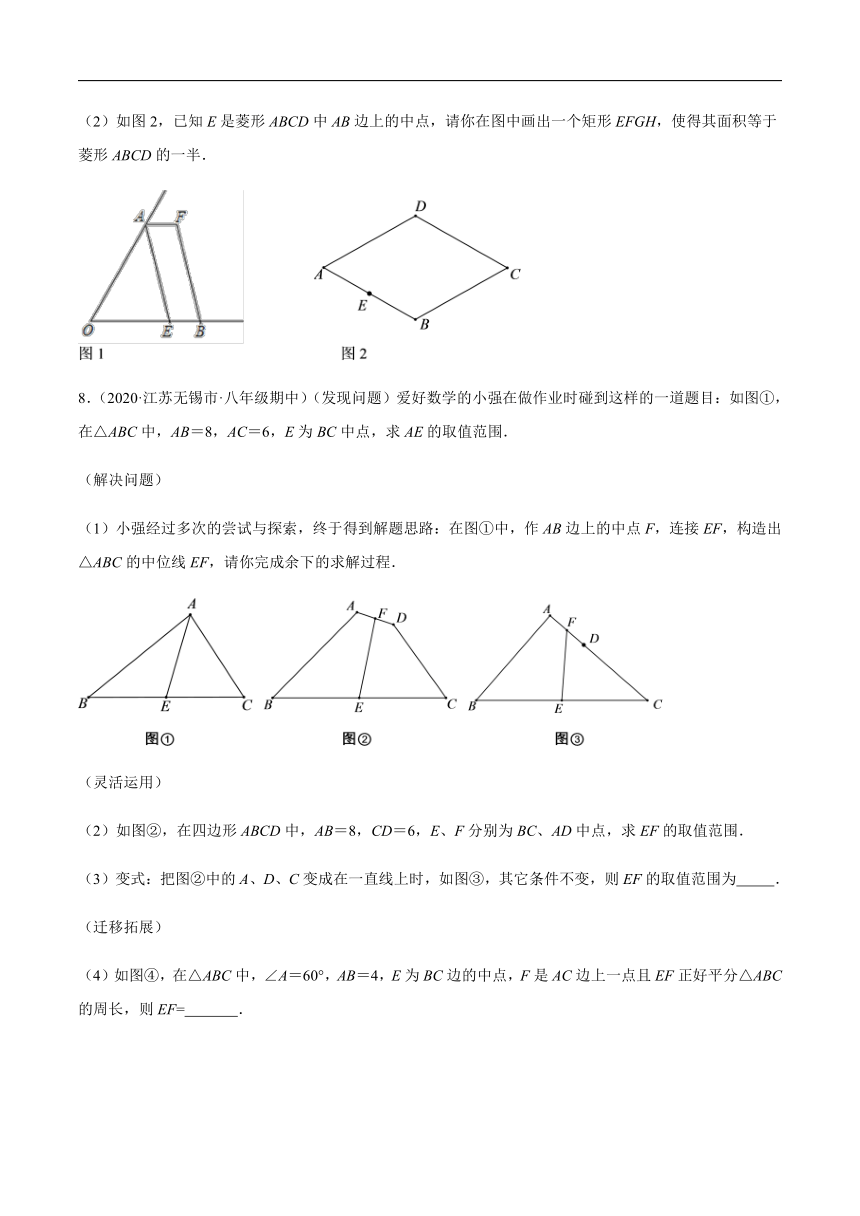
(2)如图2,已知E是菱形ABCD中AB边上的中点,请你在图中画出一个矩形EFGH,使得其面积等于菱形ABCD的一半.
8.(2020·江苏无锡市·八年级期中)(发现问题)爱好数学的小强在做作业时碰到这样的一道题目:如图①,在△ABC中,AB=8,AC=6,E为BC中点,求AE的取值范围.
(解决问题)
(1)小强经过多次的尝试与探索,终于得到解题思路:在图①中,作AB边上的中点F,连接EF,构造出△ABC的中位线EF,请你完成余下的求解过程.
(灵活运用)
(2)如图②,在四边形ABCD中,AB=8,CD=6,E、F分别为BC、AD中点,求EF的取值范围.
(3)变式:把图②中的A、D、C变成在一直线上时,如图③,其它条件不变,则EF的取值范围为
.
(迁移拓展)
(4)如图④,在△ABC中,∠A=60°,AB=4,E为BC边的中点,F是AC边上一点且EF正好平分△ABC的周长,则EF=
.
9.(2020·南通市八一中学八年级期中)如图①,将正方形ABOD放在平面直角坐标系中,O是坐标原点,点D的坐标为(2,3),
(1)点B的坐标为
;
(2)若点P为对角线BD上的动点,作等腰直角三角形APE,使∠PAE=90°,如图②,连接DE,则BP与DE的关系(位置与数量关系)是
,并说明理由;
(3)在(2)的条件下,再作等边三角形APF,连接EF、FD,如图③,在
P点运动过程中当EF取最小值时,此时∠DFE=
°;
(4)在(1)的条件下,点
M在
x
轴上,在平面内是否存在点N,使以
B、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
10.(2020·扬州市江都区实验初级中学八年级期中)如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且∠PAE=∠E,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数.
11.(2020·无锡市东林中学八年级期中)已知矩形ABCD中,AB=8cm,BC=16cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE,判断四边形AFCE的形状,并说明理由;
(2)如图2,动点P、Q分别从A、C两点同时出发,P点沿着A→F→B→A匀速运动,Q点沿着C→D→E→C匀速运动,在运动过程中:
①
已知点P的速度为10cm/s,点Q的速度为8cm/s,运动时间为t秒,问当t为何值时,点A,C,P,Q组成的四边形为平行四边形?
②
点P,Q的运动路程分别为a,b(单位:cm,ab≠0),问当a,b满足怎样的关系式时,点A,C,P,Q组成的四边形为平行四边形?
12.(2020·江阴市利港中学八年级月考)如图1,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点A(0,3)、点C(-4,0).
(1)若把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E,求折痕DE的长;
(2)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请直接写出点Q的坐标;若不存在,请说明理由;
(3)如图2,若M为AC边上的一动点,在OA上取一点N(0,1),将矩形OABC绕点O顺时针旋转一周,在旋转的过程中,M的对应点为M1,请直接写出NM1的最大值和最小值.
13.(2020·湖北十堰市·八年级期末)如图,在矩形ABCD中,直线l经过对角线AC的中点O(直线l不与线段AC重合),与AB、CD交于点E、F.
(1)求证:BE
=
DF;
(2)当直线l⊥AC时,若AD
=
4,AB
=
6,求CF的长.
14.(2019·无锡市江南中学八年级期中)在平面直角坐标系,已知线段AB,且A(-4,0)、B(-3,-3),如图①所示,平移线段AB到线段CD,使点A的对应点是点D,点B的对应点是点C.
(1)若点C的坐标为(1,1),则点D的坐标为_____;
(2)若点C在第四象限,点D在y轴上,连接AC、BD交于点P,如图②所示,且S△PCD=3.5,求此时点C、点D的坐标.
(3)在(2)的条件下,点M在y轴上,平面内是否存在点N,使得以点A、D、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标.
16.(2019·无锡市天一实验学校八年级期中)(认识概念)
点P、Q分别是两个图形G1、G2上的任意一点,当P、Q两点之间的距离最小时,我们把这个最小距离叫作图形G1、G2的亲密距离,记为d(G1,G2).例如,如果点M、N分别是两条相交直线a、b上的任意一点,则d(a,b)=0
(初步运用)
如图1,长方形四个顶点分别是点A、B、C、D,边AB=CD=5,AD=BC=3.那么d(AB,CD)=___,d(AD,BC)=_____,d(AD,AB)=_____.
(深入探究)
(1)在图1中,如果将线段CD沿它所在直线平移(边AB不动),且使d(CD,AB)不变,那么线段CD的中点偏离它原来位置的最大距离为______;
(2)如图2,线段AB∥直线CD,AB=1,点A到CD的距离为3,将线段AB绕点A旋转90°后的对应线段为AB′,则d(AB′,CD)=______.
(2019·无锡市天一实验学校八年级期中)
(1)方法回顾
在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
第一步添加辅助线:如图1,在△ABC中,延长DE
(D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
第二步证明△ADE≌△CFE,再证四边形DBCF是平行四边形,从而得到DE∥BC,DE=BC.
(2)问题解决
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)拓展研究
如图3,在四边形ABCD中,∠A=100°,∠D=110°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=4,DF=,∠GEF=90°,求GF的长.
18.(2019·江苏无锡市·八年级期中)如图,已知.
(1)请用直尺(不带刻度)和圆规作菱形,要求点、、分别在边,和上(不写作法,保留作图痕迹);
(2)若,,,请利用备用图求菱形的边长.
19.(2019·江苏无锡市·八年级期中)如图1,在平面直角坐标系中,四边形是正方形,点,点,是边上的一个动点(不与、重合),连接,点关于直线的对称点为,连接,延长交于点,过点作交的延长线于点,设.
(图1)
(图2)
(1)求证:;
(2)求点的坐标(用含有的代数式表示);
(3)如图2,过点作交于点,试判断的长度是否随着点位置的变化而改变?如果不改变,请求出的长度;如果改变,请说明理由.
参考答案
1.解:(1)如图所示:①连接AC、BD交于O,②连接EO并延长交AD于F点,
(2)如图所示:①连接AC、BD交于点G;②连接DG并延长交AB于点F,由轴对称可知,DF⊥AB,
2.(1)①∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AB=AD,∠BAD=60°,
∴△ABD是等边三角形;
②由①得△ABD是等边三角形,
∴AB=BD,
∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AC=AE,BC=DE,
又∵AC=BC,
∴EA=ED,
∴点B、E在AD的线段垂直平分线上,
∴BE是AD的线段垂直平分线,
∵点F在BE的延长线上,
∴BF⊥AD,?AF=DF;
③由②知BF⊥AD,AF=DF,
∴AF=DF=6,
∵AE=AC=10,
∴EF=8,
∵在等边三角形ABD中,BF=,
∴BE=BF﹣EF=;
(2)如图所示,
∵∠DAG=∠ACB,∠DAE=∠BAC,
∴∠ACB+∠BAC+∠ABC=∠DAG+∠DAE+∠ABC=180°,
又∵∠DAG+∠DAE+∠BAE=180°,
∴∠BAE=∠ABC,
∵AC=BC=AE,
∴∠BAC=∠ABC,
∴∠BAE=∠BAC,
∴AB⊥CE,且CH=HE=CE,
∵AC=BC,
∴AH=BH=AB=6,
∴CH=
则CE=2CH=16,BE=10,
∴BE+CE=10+16=26.
3.(1)证明:如图1,过E作MN∥AB,交AD于M,交BC于N,
∵四边形ABCD是正方形,
∴AD∥BC,AB⊥AD,
∴MN⊥AD,MN⊥BC,
∴∠AME=∠FNE=90°=∠NFE+∠FEN,
∵AE⊥EF,
∴∠AEF=∠AEM+∠FEN=90°,
∴∠AEM=∠NFE,
∵∠DBC=45°,∠BNE=90°,
∴BN=EN=AM,
∴△AEM≌△EFN(AAS),
∴AE=EF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE,
∴CE=EF;
如图2,同理可证明∠BAE=∠CFE,
∵BD是正方形ABCD的对角线,
∴∠ABE=∠CBE=45°
又AB=CB,BE=BE
∴△BEA≌△BEC
∴∠BAE=∠BCE
∴∠CFE=∠FCE
∴CE=FE
因此,点E在整个运动过程中,总有:CE=EF;
(2)解:在Rt△BCD中,由勾股定理得:,
∴,
由题意得:BE=2x,
∴,
由(1)知:AE=EF=EC,
分两种情况:
①当时,如图3,
∵AB=MN=10,
∴ME=FN=10-x,
∴BF=FN-BN=10-x-x=10-2x,
∴;
②当时,如图4,过E作EN⊥BC于N,
∴EN=BN=x,
∴FN=CN=10-x,
∴BF=BC-2CN=10-2(10-x)=2x-10,
∴;
综上,y与x之间关系的函数表达式为:
y=
4.(1)根据题意作图如下:
(2)根据题意作图如下:
解:∵直尺是矩形
∴∠AHC=90°
∴AH为中边上的高.
5.解:(1)如图1,
∵BE⊥l,l∥k,
∴∠AEB=∠BFC=90°,
又四边形ABCD是正方形,
∴∠1+∠2=90°,AB=BC,∠2+∠3=90°,
∴∠1=∠3,
∴在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=2,
∵BE=d1+d2=2+3=5,
∴AB=,
∴正方形的边长是;
(2)如图,连接AC
∵四边形ABCD是菱形
∴CD=AD
∵
∴△ACD是等边三角形
∴AD=AC,∠CAD=60°
∵是等边三角形
∴AE=AF,∠EAF=60°
∵∠FAD=∠CAD-∠CAF
=60°-∠CAF
∠EAC=∠EAF-∠CAF
=60°-∠CAF
∴∠FAD=∠EAC
∴在△ACE和△ADF中,
,
∴△ACE≌△ADF(SAS),
∴.
6.(1)t=3
-;(2)t=
;(3)m=
.
7.解:(1)如图所示:AD即为∠AOB的角平分线;
(2)如图2所示:四边形EFMN即为菱形.
8.(1)解:
∵E
为
BC
中点,F为
AB
中点,
∴EF=AC,
∵AB=8,AC=6,
∴AF=AB=4,EF=AC=3,
在△AEF中,两边之和大于第三边,两边之差小于第三边,
∴4-3<AE<4+3,
即,1<AE<7;
(2)解:连接BD,取BD
中点G,连接FG、EG,
∵E、F分别为BC、AD中点,
∴FG=AB,EG=DC,
∵AB=8,CD=6,
∴FG=4,EG=3,
在△GEF中,4-3<EF<4+3,
即1<EF<7.
(3)如图,连接BD,取BD的中点H,连接HF,HE,
∵E、F分别为BC、AD中点,
∴,
∴在△DHE中,,
即EF的取值范围为,
故答案为:;
(4)在线段CF上取一点M,使得FM=AF,连接BM,取BM的中点N,连接FN,EN,
∴F为线段AM的中点,
∵E为BC中点,
∴FN∥AB,且,EN∥AC,且,BE=EC,
∵∠A=60°,AB=4,
∴FN=2,∠FNE=120°,
∵EF正好平分△ABC的周长,
∴,
∴,
∴CM=4,
∴NE=2,
∴△FNE为等腰三角形,且∠NFE=∠NEF=30°,
过点N作NO⊥EF于点O,
则FO=OE=,
∴,
故答案为:.
9.解(1):过点B作BE⊥x轴于E,过点D作DF⊥x轴于F,
∵ABOD为正方形,O是坐标原点,点D的坐标为(2,3),
∴OB=OD,∠BE0=∠DFO,∠BOE=∠ODF,
∴△BEO≌△OFD,
∴OF=BE,OE=FD,
∴点B的坐标为(-3,2),
故答案为:(-3,2);
(2)BP与DE的关系是:垂直且相等;
证明:如图,
∵正方形ABOD,
∴∠BAD=90°,AB=AD,
∵∠PAE=90°,
∴∠BAD-∠3=∠PAE-∠3,
即∠1=∠2,
∵AP=AE,
∴△ABP≌△ADE(SAS),
∴∠4=∠5,
BP=DE,
∵∠4+∠6=90°,
∴∠5+∠6=90°,
即∠BDE=90°,
∴BP⊥DE,
∴BP与DE垂直且相等,
故答案为:垂直且相等;
(3)∵△APF为等边三角形,△PAE为等腰直角三角形,且∠PAE=90°,
∴AF=AE,∠FAE=30°,
即△AFE为等腰三角形,且EF为底边,
∴当EF最小时,AF=AE应该取最小值,即AP应当取最小值,
∵四边形ABOD为矩形,BD为ABOD一条对角线,
∴当AP⊥BD时,EF有最小值,如下图所示,
∴AP=PD=AE,∠PAD=∠APD=90°,
∴∠EAF=∠DPF=30°,
又∵AF=PF,
∴△AFE≌△PFE,
∴∠PFD=∠AFE=75°,
∴∠EFD=360°-75°-75°-60°=150°,
即,当EF取最小值时,∠DFE=150°,
故答案为:150;
(4)∵D(2,3),
∴OD=,
∴BD=,
①当BD为菱形的边时,
(Ⅰ)如图,作BQ⊥x轴于Q,
MB=BD=,在Rt△BQM中根据勾股定理,可得M1(-3,0)、M2(--3,0),
∵B向右平移5个单位再向上平移1个单位得到D,
∴N1(+2,1)、N2(-+2,1);
(Ⅱ)如图,作TP垂直x轴于P,
MD=BD=,在Rt△DPM中根据勾股定理,可得M3(+2,0)、M4(-+2,0),
∵D向左平移5个单位再向下平移1个单位得到B,
∴N3(-3,-1)、N4(--3,-1)
②当BD为菱形的对角线时,M与O重合,此时N与A重合,
如图,作AJ∥x轴交y轴于R,过点D作JK⊥x轴垂足为K,交AJ于点J,
易证△ALD≌△DKO,
∴JK=5,
在Rt△ARO中使用勾股定理,即可求N5(-1,5),
综上所述,点N坐标为(+2,1)或(-+2,1)或(-3,-1)或(--3,-1)或(-1,5).
10.(1)证明:在正方形ABCD中,AD=DC,∠ADP=∠CDP=45°
在△ADP和△CDP中
∴△ADP≌△CDP(SAS)
∴PA=PC
∵∠PAE=∠E
∴PA=PE
∴PC=PE
(2)解:
在正方形ABCD中,∠ADC=90°
∴∠EDF=90°
由(1)知,△ADP≌△CDP
∴∠DAP=∠DCP
∵∠DAP=∠E
∴∠DCP=∠E
∵∠CFP=∠EFD(对顶角相等)
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E
即∠CPE=∠EDF=90°
11.(1)四边形AFCE为菱形
证明:∵四边形ABCD是矩形
∴AD∥BC
∴∠CAD=∠ACB,∠AEF=∠CFE
∵EF垂直平分AC
∴OA=OC
∴△AOE≌△COF
∴OE=OF
∴四边形AFCE为平行四边形
又∵EF⊥AC
∴四边形AFCE为菱形
(2)解:①当P点在AF上时,Q点在CD上,
此时A、C、P、Q四点不可能构成平行四边形
同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒10cm,点Q的速度为每秒8cm,运动时间为t秒
∴PC=CF+FP=AF+FP=10t,QA=24﹣8t
∴10t=24﹣8t
∴t=s
②由题意得,四边形APCO是平行四边形时,点P、Q在互相平行的对应边上.分三种情况:
(i)如图1,当P点在AF上、Q点在CE上时,
AP=CQ,即a=24﹣b,得a+b=24
(ii)如图2,当P点在BF上、Q点在DE上时,
AQ=CP,即24﹣b=a,得a+b=24
(iii)如图3,当P点在AB上、Q点在CD上时,
AP=CQ,即24﹣a=b,得a+b=24
综上所述,a与b满足的数量关系式是a+b=24(ab≠0)
12.(1);(2)当DE是菱形的对角线时,Q1(0,3),当DE是菱形的边时,Q2(,3),Q3(-,3),Q4(-,-3);(3)最大值是5,最小值是.
13.(1)证明:在矩形ABCD中,AB∥CD,AB=CD
∴∠EAO
=
∠FCO
又∵∠AOE
=∠COF,AO
=
CO
∴△AEO≌△CFO
∴EA
=
FC
∴BE=DF
(2)连接AF、CE
∵
EA
=
FC,EA
∥
FC
∴四边形AFCE为平行四边形
∵EF⊥AC,
∴□AFCE为菱形
∴设AF
=
CF
=
x
在矩形ABCD中,∠D=90°,x2=
42
+
(6-x)2
即
14.(1)(0,4);(2)D(0,2),C(1,-1);(3).
16.【初步运用】d(AB,CD)=3,d(AD,BC)=5,d(AD,AB)=0;【深入探究】(1)CD的原中点E和平称后的中点F的最大距离为:5;(2)d(AB′,CD)=2或3,
17.问题解决:GF=5;拓展研究:GF=.
18.(1)作的平分线,交于点.
作的垂直平分线,分别交、于点、.
(2)设、相交于点.
∵四边形是菱形,
∴,又∵.
∴是等边三角形.
又∵,
∴,
∴,
∴.
∴在中,由勾股定理,求出.
∴,即菱形的边长为.
19.(1)连接.
∵点关于直线的对称点为点.
∴垂直平分,∴,.
∴.
∴,∴.
又∵在正方形中,有,,
∴
.
∴,∴.
(2)过点作,垂足为.
由(1)知:和.
∴,.
又∵,∴,∴.
又∵,可证.
∴,.
∴.
(3)随着点位置的变化,的长度始终保持不变.
连接.
∵.
∴,∴.
又∵是正方形的对角线.
∴.
∴.
∴.
又.
∴四边形是平行四边形.
∴.
一、解答题
1.(2020·江苏无锡市·八年级期中)按要求作图,不要求写做法,但要保留作图痕迹.
(1)如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.
(2)如图2,BE是菱形ABCD的边AD上的高,请只用直尺(不带刻度)作出菱形ABCD的边AB上的高DF.
2.(2020·江苏无锡市·八年级期中)在△ABC中,AB=12,AC=BC=10,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为D,点C的对应点为E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长.
在旋转过程中,过点D作DG垂直于直线AB,垂足为G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
3.(2020·江苏无锡市·八年级期中)如图,在正方形ABCD中,AB=5cm,E为对角线BD上一动点,连接AE、CE,过E点作EF⊥AE,交直线BC于点F,E点从B点出发,沿BD方向以每秒1cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
(1)点E在整个运动过程中,试说明总有:CE=EF;
(2)求y与x之间关系的表达式,并写出x的取值范围.
4.(2020·江苏无锡市·八年级期中)已知,如图在中,.
(1)请用无刻度的直尺和圆规,画出中边上的中线;(作图要求:保留痕迹,不写作法.)
(2)请只用无刻度的直尺,画出中边上的高,并说明理由.
5.(2020·江苏无锡市·八年级期中)已知:平行线与与与之间的距离分别为且,.我们把四个顶点分别在这四条平行线上的四边形称为“线上四边形”
(1)如图1,正方形为“线上四边形”,于点的延长线交直线于点.求正方形的边长.
(2)如图2,菱形为“线上四边形”且是等边三角形,点在直线上,连接且的延长线分别交直线于点.求证:.
6.(2020·江苏无锡市·八年级期中)如图,在矩形中,,动点从点出发,沿射线以每秒个单位的速度向点方向运动,连接,把沿翻折,得到.设点的运动时间为.
(1)若,当三点在同一直线上时,求的值;
(2)若点到直线的距离等于,求的值;
(3)若的最小值为,直接写出的值.
7.(2020·江苏无锡市·八年级期中)只用无刻度的直尺作图(保留作图痕迹,不要求写作法)
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,其中四边形AEBF是平行四边形,请你在图中画出∠AOB的平分线.
(2)如图2,已知E是菱形ABCD中AB边上的中点,请你在图中画出一个矩形EFGH,使得其面积等于菱形ABCD的一半.
8.(2020·江苏无锡市·八年级期中)(发现问题)爱好数学的小强在做作业时碰到这样的一道题目:如图①,在△ABC中,AB=8,AC=6,E为BC中点,求AE的取值范围.
(解决问题)
(1)小强经过多次的尝试与探索,终于得到解题思路:在图①中,作AB边上的中点F,连接EF,构造出△ABC的中位线EF,请你完成余下的求解过程.
(灵活运用)
(2)如图②,在四边形ABCD中,AB=8,CD=6,E、F分别为BC、AD中点,求EF的取值范围.
(3)变式:把图②中的A、D、C变成在一直线上时,如图③,其它条件不变,则EF的取值范围为
.
(迁移拓展)
(4)如图④,在△ABC中,∠A=60°,AB=4,E为BC边的中点,F是AC边上一点且EF正好平分△ABC的周长,则EF=
.
9.(2020·南通市八一中学八年级期中)如图①,将正方形ABOD放在平面直角坐标系中,O是坐标原点,点D的坐标为(2,3),
(1)点B的坐标为
;
(2)若点P为对角线BD上的动点,作等腰直角三角形APE,使∠PAE=90°,如图②,连接DE,则BP与DE的关系(位置与数量关系)是
,并说明理由;
(3)在(2)的条件下,再作等边三角形APF,连接EF、FD,如图③,在
P点运动过程中当EF取最小值时,此时∠DFE=
°;
(4)在(1)的条件下,点
M在
x
轴上,在平面内是否存在点N,使以
B、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
10.(2020·扬州市江都区实验初级中学八年级期中)如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且∠PAE=∠E,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数.
11.(2020·无锡市东林中学八年级期中)已知矩形ABCD中,AB=8cm,BC=16cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE,判断四边形AFCE的形状,并说明理由;
(2)如图2,动点P、Q分别从A、C两点同时出发,P点沿着A→F→B→A匀速运动,Q点沿着C→D→E→C匀速运动,在运动过程中:
①
已知点P的速度为10cm/s,点Q的速度为8cm/s,运动时间为t秒,问当t为何值时,点A,C,P,Q组成的四边形为平行四边形?
②
点P,Q的运动路程分别为a,b(单位:cm,ab≠0),问当a,b满足怎样的关系式时,点A,C,P,Q组成的四边形为平行四边形?
12.(2020·江阴市利港中学八年级月考)如图1,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点A(0,3)、点C(-4,0).
(1)若把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E,求折痕DE的长;
(2)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请直接写出点Q的坐标;若不存在,请说明理由;
(3)如图2,若M为AC边上的一动点,在OA上取一点N(0,1),将矩形OABC绕点O顺时针旋转一周,在旋转的过程中,M的对应点为M1,请直接写出NM1的最大值和最小值.
13.(2020·湖北十堰市·八年级期末)如图,在矩形ABCD中,直线l经过对角线AC的中点O(直线l不与线段AC重合),与AB、CD交于点E、F.
(1)求证:BE
=
DF;
(2)当直线l⊥AC时,若AD
=
4,AB
=
6,求CF的长.
14.(2019·无锡市江南中学八年级期中)在平面直角坐标系,已知线段AB,且A(-4,0)、B(-3,-3),如图①所示,平移线段AB到线段CD,使点A的对应点是点D,点B的对应点是点C.
(1)若点C的坐标为(1,1),则点D的坐标为_____;
(2)若点C在第四象限,点D在y轴上,连接AC、BD交于点P,如图②所示,且S△PCD=3.5,求此时点C、点D的坐标.
(3)在(2)的条件下,点M在y轴上,平面内是否存在点N,使得以点A、D、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标.
16.(2019·无锡市天一实验学校八年级期中)(认识概念)
点P、Q分别是两个图形G1、G2上的任意一点,当P、Q两点之间的距离最小时,我们把这个最小距离叫作图形G1、G2的亲密距离,记为d(G1,G2).例如,如果点M、N分别是两条相交直线a、b上的任意一点,则d(a,b)=0
(初步运用)
如图1,长方形四个顶点分别是点A、B、C、D,边AB=CD=5,AD=BC=3.那么d(AB,CD)=___,d(AD,BC)=_____,d(AD,AB)=_____.
(深入探究)
(1)在图1中,如果将线段CD沿它所在直线平移(边AB不动),且使d(CD,AB)不变,那么线段CD的中点偏离它原来位置的最大距离为______;
(2)如图2,线段AB∥直线CD,AB=1,点A到CD的距离为3,将线段AB绕点A旋转90°后的对应线段为AB′,则d(AB′,CD)=______.
(2019·无锡市天一实验学校八年级期中)
(1)方法回顾
在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
第一步添加辅助线:如图1,在△ABC中,延长DE
(D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
第二步证明△ADE≌△CFE,再证四边形DBCF是平行四边形,从而得到DE∥BC,DE=BC.
(2)问题解决
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)拓展研究
如图3,在四边形ABCD中,∠A=100°,∠D=110°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=4,DF=,∠GEF=90°,求GF的长.
18.(2019·江苏无锡市·八年级期中)如图,已知.
(1)请用直尺(不带刻度)和圆规作菱形,要求点、、分别在边,和上(不写作法,保留作图痕迹);
(2)若,,,请利用备用图求菱形的边长.
19.(2019·江苏无锡市·八年级期中)如图1,在平面直角坐标系中,四边形是正方形,点,点,是边上的一个动点(不与、重合),连接,点关于直线的对称点为,连接,延长交于点,过点作交的延长线于点,设.
(图1)
(图2)
(1)求证:;
(2)求点的坐标(用含有的代数式表示);
(3)如图2,过点作交于点,试判断的长度是否随着点位置的变化而改变?如果不改变,请求出的长度;如果改变,请说明理由.
参考答案
1.解:(1)如图所示:①连接AC、BD交于O,②连接EO并延长交AD于F点,
(2)如图所示:①连接AC、BD交于点G;②连接DG并延长交AB于点F,由轴对称可知,DF⊥AB,
2.(1)①∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AB=AD,∠BAD=60°,
∴△ABD是等边三角形;
②由①得△ABD是等边三角形,
∴AB=BD,
∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AC=AE,BC=DE,
又∵AC=BC,
∴EA=ED,
∴点B、E在AD的线段垂直平分线上,
∴BE是AD的线段垂直平分线,
∵点F在BE的延长线上,
∴BF⊥AD,?AF=DF;
③由②知BF⊥AD,AF=DF,
∴AF=DF=6,
∵AE=AC=10,
∴EF=8,
∵在等边三角形ABD中,BF=,
∴BE=BF﹣EF=;
(2)如图所示,
∵∠DAG=∠ACB,∠DAE=∠BAC,
∴∠ACB+∠BAC+∠ABC=∠DAG+∠DAE+∠ABC=180°,
又∵∠DAG+∠DAE+∠BAE=180°,
∴∠BAE=∠ABC,
∵AC=BC=AE,
∴∠BAC=∠ABC,
∴∠BAE=∠BAC,
∴AB⊥CE,且CH=HE=CE,
∵AC=BC,
∴AH=BH=AB=6,
∴CH=
则CE=2CH=16,BE=10,
∴BE+CE=10+16=26.
3.(1)证明:如图1,过E作MN∥AB,交AD于M,交BC于N,
∵四边形ABCD是正方形,
∴AD∥BC,AB⊥AD,
∴MN⊥AD,MN⊥BC,
∴∠AME=∠FNE=90°=∠NFE+∠FEN,
∵AE⊥EF,
∴∠AEF=∠AEM+∠FEN=90°,
∴∠AEM=∠NFE,
∵∠DBC=45°,∠BNE=90°,
∴BN=EN=AM,
∴△AEM≌△EFN(AAS),
∴AE=EF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE,
∴CE=EF;
如图2,同理可证明∠BAE=∠CFE,
∵BD是正方形ABCD的对角线,
∴∠ABE=∠CBE=45°
又AB=CB,BE=BE
∴△BEA≌△BEC
∴∠BAE=∠BCE
∴∠CFE=∠FCE
∴CE=FE
因此,点E在整个运动过程中,总有:CE=EF;
(2)解:在Rt△BCD中,由勾股定理得:,
∴,
由题意得:BE=2x,
∴,
由(1)知:AE=EF=EC,
分两种情况:
①当时,如图3,
∵AB=MN=10,
∴ME=FN=10-x,
∴BF=FN-BN=10-x-x=10-2x,
∴;
②当时,如图4,过E作EN⊥BC于N,
∴EN=BN=x,
∴FN=CN=10-x,
∴BF=BC-2CN=10-2(10-x)=2x-10,
∴;
综上,y与x之间关系的函数表达式为:
y=
4.(1)根据题意作图如下:
(2)根据题意作图如下:
解:∵直尺是矩形
∴∠AHC=90°
∴AH为中边上的高.
5.解:(1)如图1,
∵BE⊥l,l∥k,
∴∠AEB=∠BFC=90°,
又四边形ABCD是正方形,
∴∠1+∠2=90°,AB=BC,∠2+∠3=90°,
∴∠1=∠3,
∴在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=2,
∵BE=d1+d2=2+3=5,
∴AB=,
∴正方形的边长是;
(2)如图,连接AC
∵四边形ABCD是菱形
∴CD=AD
∵
∴△ACD是等边三角形
∴AD=AC,∠CAD=60°
∵是等边三角形
∴AE=AF,∠EAF=60°
∵∠FAD=∠CAD-∠CAF
=60°-∠CAF
∠EAC=∠EAF-∠CAF
=60°-∠CAF
∴∠FAD=∠EAC
∴在△ACE和△ADF中,
,
∴△ACE≌△ADF(SAS),
∴.
6.(1)t=3
-;(2)t=
;(3)m=
.
7.解:(1)如图所示:AD即为∠AOB的角平分线;
(2)如图2所示:四边形EFMN即为菱形.
8.(1)解:
∵E
为
BC
中点,F为
AB
中点,
∴EF=AC,
∵AB=8,AC=6,
∴AF=AB=4,EF=AC=3,
在△AEF中,两边之和大于第三边,两边之差小于第三边,
∴4-3<AE<4+3,
即,1<AE<7;
(2)解:连接BD,取BD
中点G,连接FG、EG,
∵E、F分别为BC、AD中点,
∴FG=AB,EG=DC,
∵AB=8,CD=6,
∴FG=4,EG=3,
在△GEF中,4-3<EF<4+3,
即1<EF<7.
(3)如图,连接BD,取BD的中点H,连接HF,HE,
∵E、F分别为BC、AD中点,
∴,
∴在△DHE中,,
即EF的取值范围为,
故答案为:;
(4)在线段CF上取一点M,使得FM=AF,连接BM,取BM的中点N,连接FN,EN,
∴F为线段AM的中点,
∵E为BC中点,
∴FN∥AB,且,EN∥AC,且,BE=EC,
∵∠A=60°,AB=4,
∴FN=2,∠FNE=120°,
∵EF正好平分△ABC的周长,
∴,
∴,
∴CM=4,
∴NE=2,
∴△FNE为等腰三角形,且∠NFE=∠NEF=30°,
过点N作NO⊥EF于点O,
则FO=OE=,
∴,
故答案为:.
9.解(1):过点B作BE⊥x轴于E,过点D作DF⊥x轴于F,
∵ABOD为正方形,O是坐标原点,点D的坐标为(2,3),
∴OB=OD,∠BE0=∠DFO,∠BOE=∠ODF,
∴△BEO≌△OFD,
∴OF=BE,OE=FD,
∴点B的坐标为(-3,2),
故答案为:(-3,2);
(2)BP与DE的关系是:垂直且相等;
证明:如图,
∵正方形ABOD,
∴∠BAD=90°,AB=AD,
∵∠PAE=90°,
∴∠BAD-∠3=∠PAE-∠3,
即∠1=∠2,
∵AP=AE,
∴△ABP≌△ADE(SAS),
∴∠4=∠5,
BP=DE,
∵∠4+∠6=90°,
∴∠5+∠6=90°,
即∠BDE=90°,
∴BP⊥DE,
∴BP与DE垂直且相等,
故答案为:垂直且相等;
(3)∵△APF为等边三角形,△PAE为等腰直角三角形,且∠PAE=90°,
∴AF=AE,∠FAE=30°,
即△AFE为等腰三角形,且EF为底边,
∴当EF最小时,AF=AE应该取最小值,即AP应当取最小值,
∵四边形ABOD为矩形,BD为ABOD一条对角线,
∴当AP⊥BD时,EF有最小值,如下图所示,
∴AP=PD=AE,∠PAD=∠APD=90°,
∴∠EAF=∠DPF=30°,
又∵AF=PF,
∴△AFE≌△PFE,
∴∠PFD=∠AFE=75°,
∴∠EFD=360°-75°-75°-60°=150°,
即,当EF取最小值时,∠DFE=150°,
故答案为:150;
(4)∵D(2,3),
∴OD=,
∴BD=,
①当BD为菱形的边时,
(Ⅰ)如图,作BQ⊥x轴于Q,
MB=BD=,在Rt△BQM中根据勾股定理,可得M1(-3,0)、M2(--3,0),
∵B向右平移5个单位再向上平移1个单位得到D,
∴N1(+2,1)、N2(-+2,1);
(Ⅱ)如图,作TP垂直x轴于P,
MD=BD=,在Rt△DPM中根据勾股定理,可得M3(+2,0)、M4(-+2,0),
∵D向左平移5个单位再向下平移1个单位得到B,
∴N3(-3,-1)、N4(--3,-1)
②当BD为菱形的对角线时,M与O重合,此时N与A重合,
如图,作AJ∥x轴交y轴于R,过点D作JK⊥x轴垂足为K,交AJ于点J,
易证△ALD≌△DKO,
∴JK=5,
在Rt△ARO中使用勾股定理,即可求N5(-1,5),
综上所述,点N坐标为(+2,1)或(-+2,1)或(-3,-1)或(--3,-1)或(-1,5).
10.(1)证明:在正方形ABCD中,AD=DC,∠ADP=∠CDP=45°
在△ADP和△CDP中
∴△ADP≌△CDP(SAS)
∴PA=PC
∵∠PAE=∠E
∴PA=PE
∴PC=PE
(2)解:
在正方形ABCD中,∠ADC=90°
∴∠EDF=90°
由(1)知,△ADP≌△CDP
∴∠DAP=∠DCP
∵∠DAP=∠E
∴∠DCP=∠E
∵∠CFP=∠EFD(对顶角相等)
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E
即∠CPE=∠EDF=90°
11.(1)四边形AFCE为菱形
证明:∵四边形ABCD是矩形
∴AD∥BC
∴∠CAD=∠ACB,∠AEF=∠CFE
∵EF垂直平分AC
∴OA=OC
∴△AOE≌△COF
∴OE=OF
∴四边形AFCE为平行四边形
又∵EF⊥AC
∴四边形AFCE为菱形
(2)解:①当P点在AF上时,Q点在CD上,
此时A、C、P、Q四点不可能构成平行四边形
同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒10cm,点Q的速度为每秒8cm,运动时间为t秒
∴PC=CF+FP=AF+FP=10t,QA=24﹣8t
∴10t=24﹣8t
∴t=s
②由题意得,四边形APCO是平行四边形时,点P、Q在互相平行的对应边上.分三种情况:
(i)如图1,当P点在AF上、Q点在CE上时,
AP=CQ,即a=24﹣b,得a+b=24
(ii)如图2,当P点在BF上、Q点在DE上时,
AQ=CP,即24﹣b=a,得a+b=24
(iii)如图3,当P点在AB上、Q点在CD上时,
AP=CQ,即24﹣a=b,得a+b=24
综上所述,a与b满足的数量关系式是a+b=24(ab≠0)
12.(1);(2)当DE是菱形的对角线时,Q1(0,3),当DE是菱形的边时,Q2(,3),Q3(-,3),Q4(-,-3);(3)最大值是5,最小值是.
13.(1)证明:在矩形ABCD中,AB∥CD,AB=CD
∴∠EAO
=
∠FCO
又∵∠AOE
=∠COF,AO
=
CO
∴△AEO≌△CFO
∴EA
=
FC
∴BE=DF
(2)连接AF、CE
∵
EA
=
FC,EA
∥
FC
∴四边形AFCE为平行四边形
∵EF⊥AC,
∴□AFCE为菱形
∴设AF
=
CF
=
x
在矩形ABCD中,∠D=90°,x2=
42
+
(6-x)2
即
14.(1)(0,4);(2)D(0,2),C(1,-1);(3).
16.【初步运用】d(AB,CD)=3,d(AD,BC)=5,d(AD,AB)=0;【深入探究】(1)CD的原中点E和平称后的中点F的最大距离为:5;(2)d(AB′,CD)=2或3,
17.问题解决:GF=5;拓展研究:GF=.
18.(1)作的平分线,交于点.
作的垂直平分线,分别交、于点、.
(2)设、相交于点.
∵四边形是菱形,
∴,又∵.
∴是等边三角形.
又∵,
∴,
∴,
∴.
∴在中,由勾股定理,求出.
∴,即菱形的边长为.
19.(1)连接.
∵点关于直线的对称点为点.
∴垂直平分,∴,.
∴.
∴,∴.
又∵在正方形中,有,,
∴
.
∴,∴.
(2)过点作,垂足为.
由(1)知:和.
∴,.
又∵,∴,∴.
又∵,可证.
∴,.
∴.
(3)随着点位置的变化,的长度始终保持不变.
连接.
∵.
∴,∴.
又∵是正方形的对角线.
∴.
∴.
∴.
又.
∴四边形是平行四边形.
∴.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
