2020-2021学年苏科版八年级下册数学 9.5三角形的中位线 同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级下册数学 9.5三角形的中位线 同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 156.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 13:00:59 | ||
图片预览



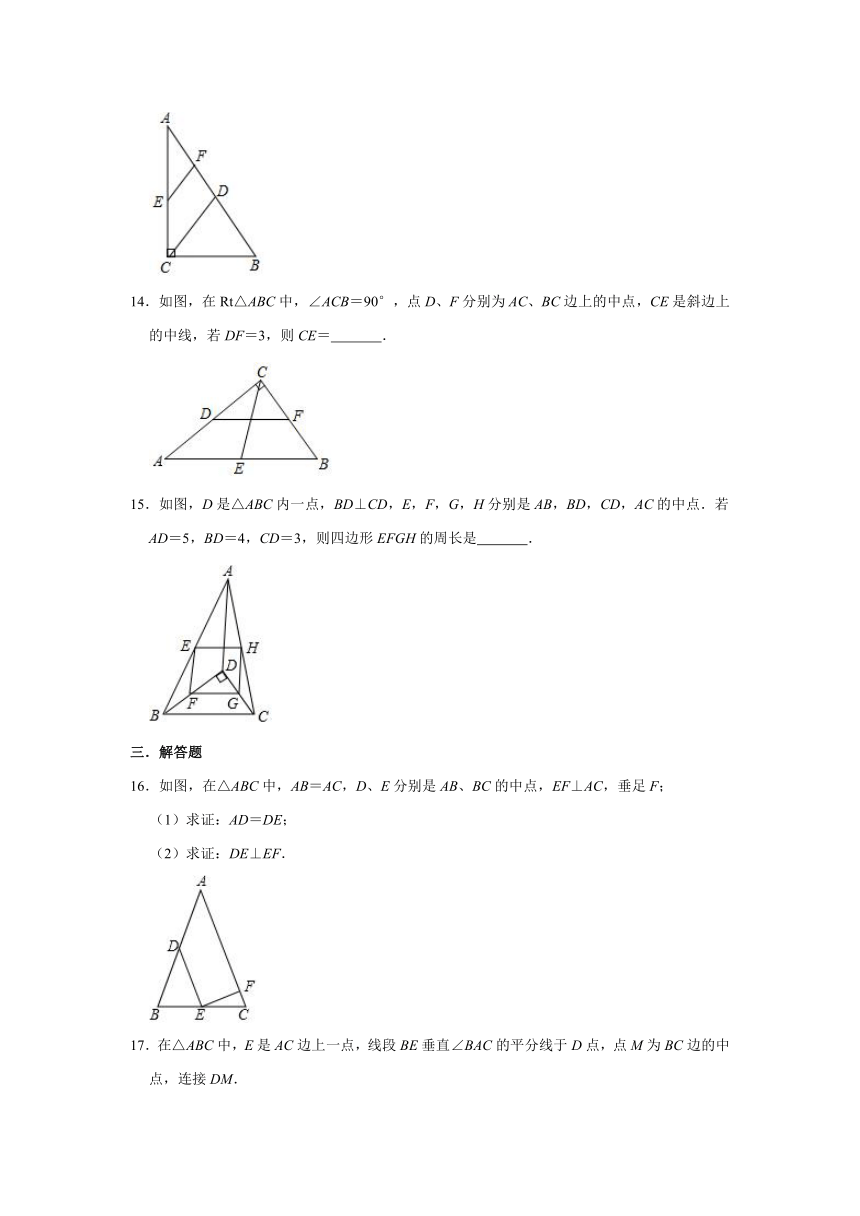

文档简介
9.5三角形的中位线
同步练习
一.选择题
1.如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是7,则△ABC的周长是( )
A.8
B.10
C.12
D.14
2.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为( )
A.2
B.4
C.6
D.8
3.如图,在△ABC中,D是AC的中点,且BD⊥AC,DE∥BC,交AB于点E,BC=7cm,AC=6cm,则△AED的周长等于( )
A.12cm
B.10cm
C.7cm
D.9cm
4.如图,在Rt△ABC中,∠B=90°,BC=5,AB=12,点D,E分别是AB,AC的中点,CF平分Rt△ABC的一个外角∠ACM,交DE的延长线于点F,则DF的长为( )
A.5
B.8.5
C.9
D.12
5.如图,△ABC是等边三角形,D、E、F分别是边AB、AC、BC的中点,若BC=4,则△DEF的周长等于( )
A.3
B.6
C.9
D.12
6.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.若四边形CDEF的周长是10cm,AC的长为4cm,则△ABC的周长是( )
A.28
B.24
C.14
D.18
7.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
A.1:4
B.1:5
C.1:6
D.1:7
8.如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,则下列结论错误的是( )
A.GF=AD
B.EF=AC
C.GE=BC
D.GE=GF
9.如图,△ABC周长20,D,E在边BC上,BN和CM分别是∠ABC和∠ACB的平分线,BN⊥AE,CM⊥AD,若BC=8,则MN的长为( )
A.1
B.2
C.3
D.3
10.如图,△ABC中,∠ACB=90°,点D,E分别在BC,AC边上,且AE=4,BD=6,分别连接AD,BE,点M,N分别是AD,BE的中点,连接MN,则线段MN的长( )
A.
B.3
C.3
D.
二.填空题
11.如图,在△ABC中,点D、E分别是边AB、AC的中点,连接DE,∠ABC的平分线BF交DE于点F,若AB=4,BC=6,则EF的长为
.
12.如图,在△ABC中,点D,E,F分别是边AB,BC,CA上的中点,且AB=10cm,AC=16cm,则四边形ADEF的周长等于
cm.
13.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别为AB、AC、AD的中点.若AB=6,则EF的长度为
.
14.如图,在Rt△ABC中,∠ACB=90°,点D、F分别为AC、BC边上的中点,CE是斜边上的中线,若DF=3,则CE=
.
15.如图,D是△ABC内一点,BD⊥CD,E,F,G,H分别是AB,BD,CD,AC的中点.若AD=5,BD=4,CD=3,则四边形EFGH的周长是
.
三.解答题
16.如图,在△ABC中,AB=AC,D、E分别是AB、BC的中点,EF⊥AC,垂足F;
(1)求证:AD=DE;
(2)求证:DE⊥EF.
17.在△ABC中,E是AC边上一点,线段BE垂直∠BAC的平分线于D点,点M为BC边的中点,连接DM.
(1)求证:DM=CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
18.如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系.
参考答案
一.选择题
1.解:∵点D、E分别是边AB、BC的中点,
∴BD=AB,BE=BC,DE=AC,
∴AB=2BD,BC=2BE,AC=2DE,
∴△ABC的周长=AB+BC+AC=2BD+2BE+2DE=2(BD+BE+DE)=2×△DBE的周长=2×7=14,
故选:D.
2.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵EF是△ABC的中位线,
∴EF∥BC,BC=2EF,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴ED=EB=3,
∴EF=ED+DF=4,
∴BC=2EF=8,
故选:D.
3.解:∵D是AC的中点,且BD⊥AC,
∴AB=BC=7cm,AD=AC=3cm,
∵ED∥BC,
∴AE=BE=AB=3.5cm,ED=BC=3.5cm,
∴△AED的周长=AE+ED+AD=10(cm).
故选:B.
4.解:∵∠B=90°,BC=5,AB=12,
∴AC==13,
∵D,E分别是AB,AC的中点,
∴DE=BC=2.5,EC=AC=6.5,DE∥BC,
∴∠FCM=∠EFC,
∵CF平分Rt△ABC的一个外角∠ACM,
∴∠FCM=∠FCE,
∴∠EFC=∠FCE,
∴EF=EC=6.5,
∴DF=DE+EF=9,
故选:C.
5.解:∵D、E、F分别是AB、AC、BC的中点,AB=BC=AC=4,
∴DE=2,EF=2,DF=2,
∴△DEF的周长=2+2+2=6,
故选:B.
6.解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,DE∥BC,
∵DE∥BC,EF∥DC,
∴四边形CDEF为平行四边形,
∴CD+DE=×10=5,
在Rt△ACB中,D是AB的中点,
∴AB=2CD,
∴AB+BC=2CD+2DE=2(CD+DE)=10,
∵AC=4,
∴△ABC的周长=AB+BC+AC=14(cm),
故选:C.
7.解:连接DE,连接并延长EP交BC于点F,
∵DE是△ABC中位线,
∴DE=BC,AE=BE,AD=CD,
∴∠EDB=∠DBF,
∵P、Q是BD、CE的中点,
∴DP=BP,
∵在△DEP与△BFP中,
,
∴△DEP≌△BFP(ASA),
∴BF=DE=BC,P是EF中点,
∴FC=BC,
PQ是△EFC中位线,
PQ=FC,
∴PQ:BC=1:4.
故选:A.
8.解:∵E,F,G分别是AB,CD,AC的中点,
∴,,,
故选项A,C正确,
∵AD=BC,
∴GE=GF,
故选项D正确,
∵EF不一定等于AG,
故选项B不正确;
故选:B.
9.解:∵BN是∠ABC的平分线,
∴∠ABN=∠EBN,
在△ABN和△EBN中,
,
∴△ABN≌△EBN(ASA),
∴BE=BA,AN=NE,
同理可得,CD=CA,AM=MD,
∵△ABC周长20,
∴AB+AC+BC=20,
∴AB+AC=20﹣BC=12,
∴DE=AB+AC﹣BC=4,
∵AN=NE,AM=MD,
∴MN是△ADE的中位线,
∴MN=DE=2,
故选:B.
10.解:取AB的中点F,连接NF、MF,
△ABC中,∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵AM=MD,AF=FB,
∴MF是△ABD的中位线,
∴MF=BD=3,MF∥BC,
∴∠AFM=∠CBA,
同理,NF=AE=2,NF∥CC,
∴∠BFN=∠CAB,
∴∠AFM+∠BFN=∠CAB+∠CBA=90°,
∴∠MFN=90°,
∴MN==,
故选:D.
二.填空题
11.解:连接AF并延长交BC于H,
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DE=BC=3,AF=FH,
在△BFA和△BFH中,
,
∴△BFA≌△BFH(AAS),
∴BH=AB=4,
∵AD=DB,AF=FH,
∴DF=BH=2,
∴EF=DE﹣DF=1,
故答案为:1.
12.解:∵点D,E,F分别是边AB,BC,CA上的中点,
∴DE,EF都是△ABC的中位线,
∴DE=AC=8cm,DE∥AC,EF=AB=5cm,EF∥AB,
∴四边形ADEF是平行四边形,
∴四边形ADEF的周长=2(DE+EF)=2×13=26(cm).
故答案为:26.
13.解:在Rt△ABC中,D为AB的中点,
∴CD=AB=3,
∵E、F分别为AC、AD的中点,
∴EF是△ACD的中位线,
∴EF=CD=,
故答案为:.
14.解:∵D,F分别为AC,BC的中点,
∴DF是△ABC的中位线,
∴AB=2DF=6,
在Rt△ABC中,E为AB的中点,
∴EC=AB=3,
故答案为:3.
15.解:在Rt△BDC中,BD=4,CD=3,
∴BC==5,
∵F,G分别是BD,CD的中点,
∴FG是△DBC的中位线,
∴FG=BC=2.5,
同理,EF=AD=2.5,EH=BC=2.5,HG=AD=2.5,
∴四边形EFGH的周长=FG+EF+EH+HG=10,
故答案为:10.
三.解答题
16.解:(1)∵AB=AC,
∴∠B=∠C,
∵D、E分别是AB、BC的中点,
∴AD=AB,DE=AC,
∴AD=DE;
(2)∵D、E分别是AB、BC的中点,
∴DE∥AC,
∵EF⊥AC,
∴DE⊥EF.
17.(1)证明:在△ADB和△ADE中,
,
∴△ADB≌△ADE(ASA)
∴AE=AB,BD=DE,
∵BD=DE,BM=MC,
∴DM=CE;
(2)解:在Rt△ADB中,AB==10,
∴AE=10,
由(1)得,CE=2DM=4,
∴AC=CE+AE=14.
18.(1)证明:∵点E、F分别为DB、BC的中点,
∴EF是△BCD的中位线,
∴EF=CD,
在Rt△ABD中,点E为斜边DB的中点,
∴AE=DB,
∵DB=DC,
∴AE=EF;
(2)如图,由(1)知AE=EF,
∵AF=AE,
∴AE=EF=AF,
∴△AEF是等边三角形,
∴∠AEF=60°,
∵EF是△BCD的中位线,
∴EF∥CD,
∴∠BEF=∠BDC=β,
∴β+∠AEB=60°,
又∵∠AEB=α+∠DAE,
∴β+α+∠DAE=60°,
∵∠DAB=90°,
∴AE是斜边BD上的中线,
∴AE=DE,
∴∠DAE=α,
∴β+α+α=60°,
即2α+β=60°.
同步练习
一.选择题
1.如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是7,则△ABC的周长是( )
A.8
B.10
C.12
D.14
2.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为( )
A.2
B.4
C.6
D.8
3.如图,在△ABC中,D是AC的中点,且BD⊥AC,DE∥BC,交AB于点E,BC=7cm,AC=6cm,则△AED的周长等于( )
A.12cm
B.10cm
C.7cm
D.9cm
4.如图,在Rt△ABC中,∠B=90°,BC=5,AB=12,点D,E分别是AB,AC的中点,CF平分Rt△ABC的一个外角∠ACM,交DE的延长线于点F,则DF的长为( )
A.5
B.8.5
C.9
D.12
5.如图,△ABC是等边三角形,D、E、F分别是边AB、AC、BC的中点,若BC=4,则△DEF的周长等于( )
A.3
B.6
C.9
D.12
6.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.若四边形CDEF的周长是10cm,AC的长为4cm,则△ABC的周长是( )
A.28
B.24
C.14
D.18
7.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
A.1:4
B.1:5
C.1:6
D.1:7
8.如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,则下列结论错误的是( )
A.GF=AD
B.EF=AC
C.GE=BC
D.GE=GF
9.如图,△ABC周长20,D,E在边BC上,BN和CM分别是∠ABC和∠ACB的平分线,BN⊥AE,CM⊥AD,若BC=8,则MN的长为( )
A.1
B.2
C.3
D.3
10.如图,△ABC中,∠ACB=90°,点D,E分别在BC,AC边上,且AE=4,BD=6,分别连接AD,BE,点M,N分别是AD,BE的中点,连接MN,则线段MN的长( )
A.
B.3
C.3
D.
二.填空题
11.如图,在△ABC中,点D、E分别是边AB、AC的中点,连接DE,∠ABC的平分线BF交DE于点F,若AB=4,BC=6,则EF的长为
.
12.如图,在△ABC中,点D,E,F分别是边AB,BC,CA上的中点,且AB=10cm,AC=16cm,则四边形ADEF的周长等于
cm.
13.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别为AB、AC、AD的中点.若AB=6,则EF的长度为
.
14.如图,在Rt△ABC中,∠ACB=90°,点D、F分别为AC、BC边上的中点,CE是斜边上的中线,若DF=3,则CE=
.
15.如图,D是△ABC内一点,BD⊥CD,E,F,G,H分别是AB,BD,CD,AC的中点.若AD=5,BD=4,CD=3,则四边形EFGH的周长是
.
三.解答题
16.如图,在△ABC中,AB=AC,D、E分别是AB、BC的中点,EF⊥AC,垂足F;
(1)求证:AD=DE;
(2)求证:DE⊥EF.
17.在△ABC中,E是AC边上一点,线段BE垂直∠BAC的平分线于D点,点M为BC边的中点,连接DM.
(1)求证:DM=CE;
(2)若AD=6,BD=8,DM=2,求AC的长.
18.如图,在四边形ABCD中,∠DAB=90°,DB=DC,点E、F分别为DB、BC的中点,连接AE、EF、AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,∠CDB=β,求α,β之间的数量关系.
参考答案
一.选择题
1.解:∵点D、E分别是边AB、BC的中点,
∴BD=AB,BE=BC,DE=AC,
∴AB=2BD,BC=2BE,AC=2DE,
∴△ABC的周长=AB+BC+AC=2BD+2BE+2DE=2(BD+BE+DE)=2×△DBE的周长=2×7=14,
故选:D.
2.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵EF是△ABC的中位线,
∴EF∥BC,BC=2EF,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴ED=EB=3,
∴EF=ED+DF=4,
∴BC=2EF=8,
故选:D.
3.解:∵D是AC的中点,且BD⊥AC,
∴AB=BC=7cm,AD=AC=3cm,
∵ED∥BC,
∴AE=BE=AB=3.5cm,ED=BC=3.5cm,
∴△AED的周长=AE+ED+AD=10(cm).
故选:B.
4.解:∵∠B=90°,BC=5,AB=12,
∴AC==13,
∵D,E分别是AB,AC的中点,
∴DE=BC=2.5,EC=AC=6.5,DE∥BC,
∴∠FCM=∠EFC,
∵CF平分Rt△ABC的一个外角∠ACM,
∴∠FCM=∠FCE,
∴∠EFC=∠FCE,
∴EF=EC=6.5,
∴DF=DE+EF=9,
故选:C.
5.解:∵D、E、F分别是AB、AC、BC的中点,AB=BC=AC=4,
∴DE=2,EF=2,DF=2,
∴△DEF的周长=2+2+2=6,
故选:B.
6.解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,DE∥BC,
∵DE∥BC,EF∥DC,
∴四边形CDEF为平行四边形,
∴CD+DE=×10=5,
在Rt△ACB中,D是AB的中点,
∴AB=2CD,
∴AB+BC=2CD+2DE=2(CD+DE)=10,
∵AC=4,
∴△ABC的周长=AB+BC+AC=14(cm),
故选:C.
7.解:连接DE,连接并延长EP交BC于点F,
∵DE是△ABC中位线,
∴DE=BC,AE=BE,AD=CD,
∴∠EDB=∠DBF,
∵P、Q是BD、CE的中点,
∴DP=BP,
∵在△DEP与△BFP中,
,
∴△DEP≌△BFP(ASA),
∴BF=DE=BC,P是EF中点,
∴FC=BC,
PQ是△EFC中位线,
PQ=FC,
∴PQ:BC=1:4.
故选:A.
8.解:∵E,F,G分别是AB,CD,AC的中点,
∴,,,
故选项A,C正确,
∵AD=BC,
∴GE=GF,
故选项D正确,
∵EF不一定等于AG,
故选项B不正确;
故选:B.
9.解:∵BN是∠ABC的平分线,
∴∠ABN=∠EBN,
在△ABN和△EBN中,
,
∴△ABN≌△EBN(ASA),
∴BE=BA,AN=NE,
同理可得,CD=CA,AM=MD,
∵△ABC周长20,
∴AB+AC+BC=20,
∴AB+AC=20﹣BC=12,
∴DE=AB+AC﹣BC=4,
∵AN=NE,AM=MD,
∴MN是△ADE的中位线,
∴MN=DE=2,
故选:B.
10.解:取AB的中点F,连接NF、MF,
△ABC中,∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵AM=MD,AF=FB,
∴MF是△ABD的中位线,
∴MF=BD=3,MF∥BC,
∴∠AFM=∠CBA,
同理,NF=AE=2,NF∥CC,
∴∠BFN=∠CAB,
∴∠AFM+∠BFN=∠CAB+∠CBA=90°,
∴∠MFN=90°,
∴MN==,
故选:D.
二.填空题
11.解:连接AF并延长交BC于H,
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DE=BC=3,AF=FH,
在△BFA和△BFH中,
,
∴△BFA≌△BFH(AAS),
∴BH=AB=4,
∵AD=DB,AF=FH,
∴DF=BH=2,
∴EF=DE﹣DF=1,
故答案为:1.
12.解:∵点D,E,F分别是边AB,BC,CA上的中点,
∴DE,EF都是△ABC的中位线,
∴DE=AC=8cm,DE∥AC,EF=AB=5cm,EF∥AB,
∴四边形ADEF是平行四边形,
∴四边形ADEF的周长=2(DE+EF)=2×13=26(cm).
故答案为:26.
13.解:在Rt△ABC中,D为AB的中点,
∴CD=AB=3,
∵E、F分别为AC、AD的中点,
∴EF是△ACD的中位线,
∴EF=CD=,
故答案为:.
14.解:∵D,F分别为AC,BC的中点,
∴DF是△ABC的中位线,
∴AB=2DF=6,
在Rt△ABC中,E为AB的中点,
∴EC=AB=3,
故答案为:3.
15.解:在Rt△BDC中,BD=4,CD=3,
∴BC==5,
∵F,G分别是BD,CD的中点,
∴FG是△DBC的中位线,
∴FG=BC=2.5,
同理,EF=AD=2.5,EH=BC=2.5,HG=AD=2.5,
∴四边形EFGH的周长=FG+EF+EH+HG=10,
故答案为:10.
三.解答题
16.解:(1)∵AB=AC,
∴∠B=∠C,
∵D、E分别是AB、BC的中点,
∴AD=AB,DE=AC,
∴AD=DE;
(2)∵D、E分别是AB、BC的中点,
∴DE∥AC,
∵EF⊥AC,
∴DE⊥EF.
17.(1)证明:在△ADB和△ADE中,
,
∴△ADB≌△ADE(ASA)
∴AE=AB,BD=DE,
∵BD=DE,BM=MC,
∴DM=CE;
(2)解:在Rt△ADB中,AB==10,
∴AE=10,
由(1)得,CE=2DM=4,
∴AC=CE+AE=14.
18.(1)证明:∵点E、F分别为DB、BC的中点,
∴EF是△BCD的中位线,
∴EF=CD,
在Rt△ABD中,点E为斜边DB的中点,
∴AE=DB,
∵DB=DC,
∴AE=EF;
(2)如图,由(1)知AE=EF,
∵AF=AE,
∴AE=EF=AF,
∴△AEF是等边三角形,
∴∠AEF=60°,
∵EF是△BCD的中位线,
∴EF∥CD,
∴∠BEF=∠BDC=β,
∴β+∠AEB=60°,
又∵∠AEB=α+∠DAE,
∴β+α+∠DAE=60°,
∵∠DAB=90°,
∴AE是斜边BD上的中线,
∴AE=DE,
∴∠DAE=α,
∴β+α+α=60°,
即2α+β=60°.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
