2020-2021学年苏科版数学七年级下册 课时训练 第七章平面图形的认识(二) 单元小结小结与思考(1)(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版数学七年级下册 课时训练 第七章平面图形的认识(二) 单元小结小结与思考(1)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 176.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 17:55:23 | ||
图片预览


文档简介
小结与思考(1)
类型之一 平行线的判定和性质
1.如图7-X-1,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1的度数为
( )
图7-X-1
A.30°
B.40°
C.50°
D.60°
2.[2019·扬州]
将一张长方形纸片折叠成如图7-X-2所示的图形,若∠ABC=26°,则∠ACD= °.?
图7-X-2
3.[2019·武汉]
如图7-X-3,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF.试说明:∠E=∠F.
图7-X-3
类型之二 平行线与三角形的综合运用
4.[2019·宿迁]
一副三角尺按图7-X-4所示摆放(直角顶点C重合),边AB与CE交于点F,DE∥BC,则∠BFC的度数为
( )
图7-X-4
A.105°
B.100°
C.75°
D.60°
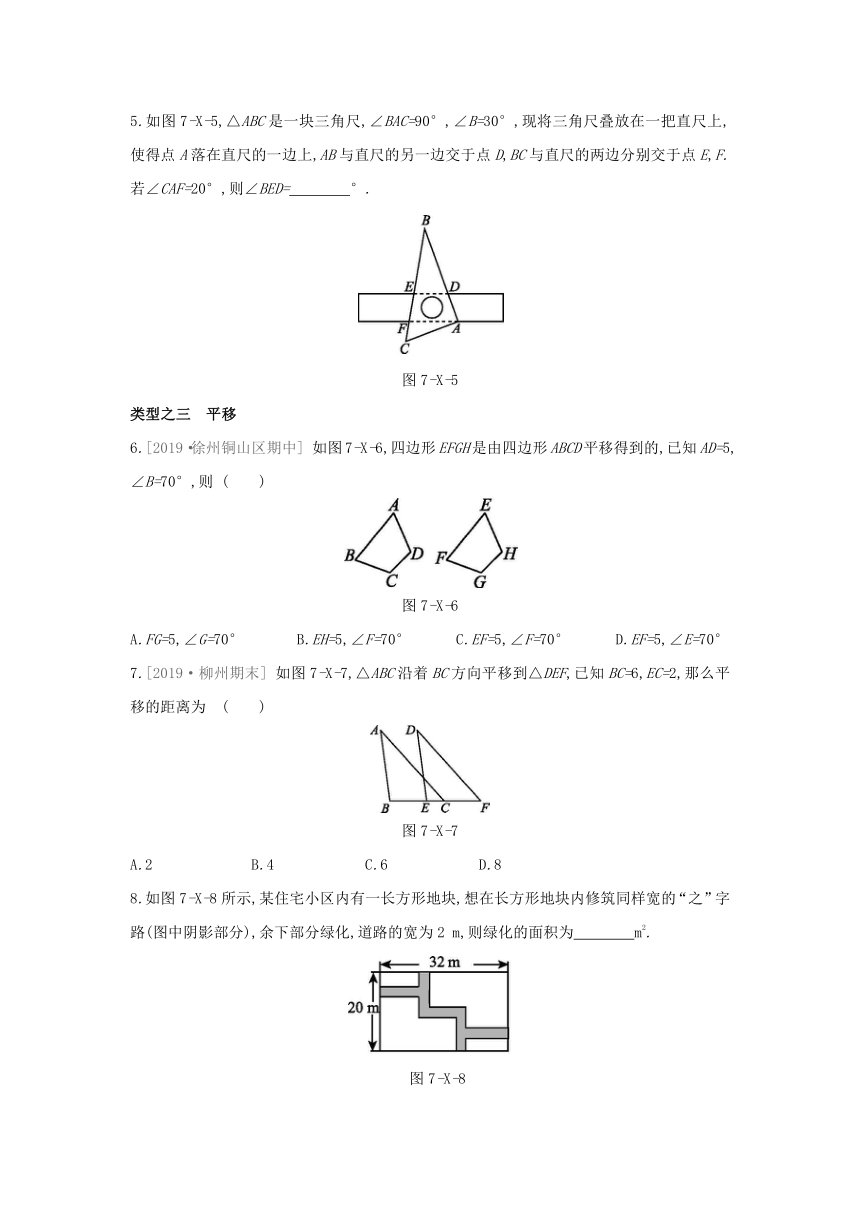
5.如图7-X-5,△ABC是一块三角尺,∠BAC=90°,∠B=30°,现将三角尺叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED= °.?
图7-X-5
类型之三 平移
6.[2019·徐州铜山区期中]
如图7-X-6,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则
( )
图7-X-6
A.FG=5,∠G=70°
B.EH=5,∠F=70°
C.EF=5,∠F=70°
D.EF=5,∠E=70°
7.[2019·柳州期末]
如图7-X-7,△ABC沿着BC方向平移到△DEF,已知BC=6,EC=2,那么平移的距离为
( )
图7-X-7
A.2
B.4
C.6
D.8
8.如图7-X-8所示,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的“之”字路(图中阴影部分),余下部分绿化,道路的宽为2
m,则绿化的面积为 m2.?
图7-X-8
9.[2020·镇江京口区月考]
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图7-X-9所示,现将△ABC平移,使点A移动到点A'处,点B',C'分别是B,C的对应点.
(1)请画出平移后的△A'B'C';
(2)若连接AA',CC',则这两条线段之间的关系是 .?
图7-X-9
类型之四 三角形的三边关系
10.[2020·福建模拟]
若三角形的三边长分别为2,x,3,且x为正整数,则这样的三角形的个数为
( )
A.2
B.3
C.4
D.5
11.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c= .?
12.小王准备用一段长30
m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为a
m,由于受地势限制,第二条边长只能是第一条边长的2倍多2
m.
(1)请用含a的式子表示第三条边长;
(2)第一条边长可以为7
m吗?请说明理由.
类型之五 三角形的内角和
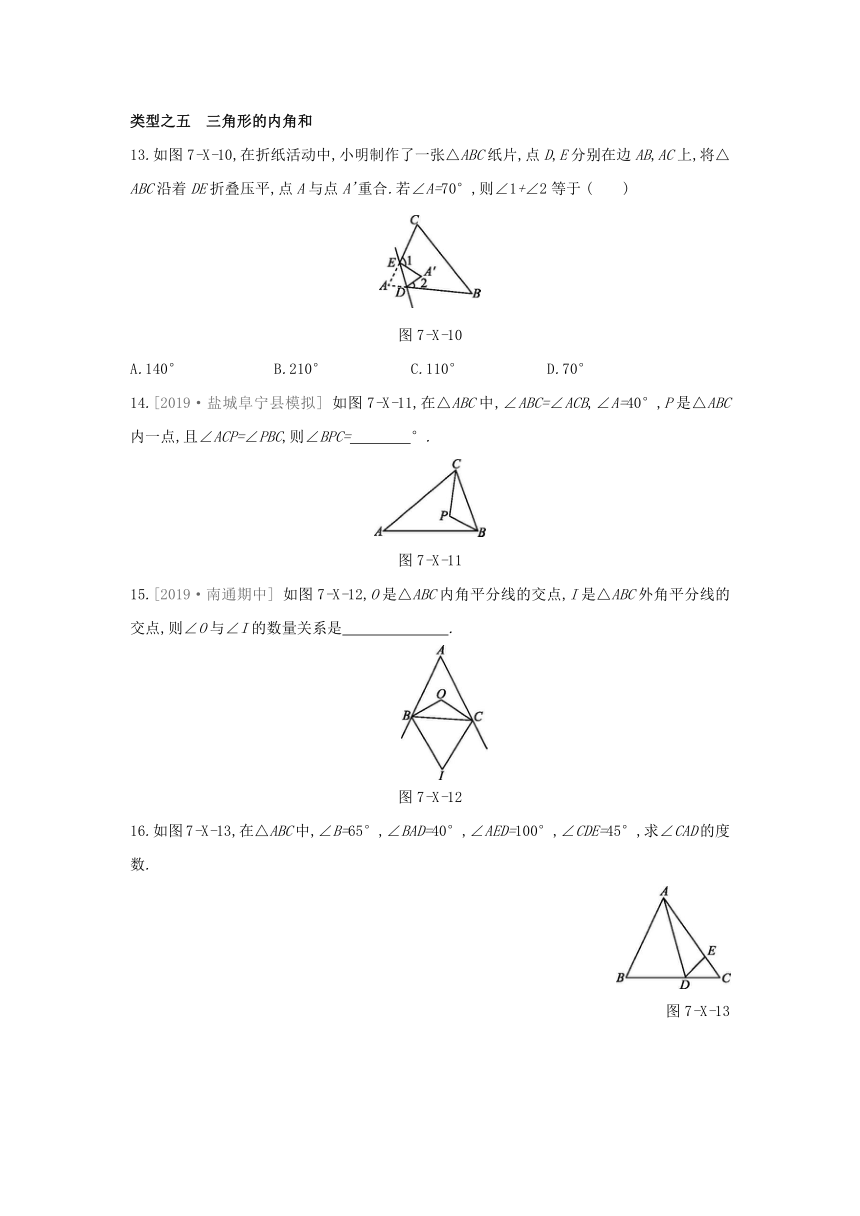
13.如图7-X-10,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,点A与点A'重合.若∠A=70°,则∠1+∠2等于
( )
图7-X-10
A.140°
B.210°
C.110°
D.70°
14.[2019·盐城阜宁县模拟]
如图7-X-11,在△ABC中,∠ABC=∠ACB,∠A=40°,P是△ABC内一点,且∠ACP=∠PBC,则∠BPC= °.?
图7-X-11
15.[2019·南通期中]
如图7-X-12,O是△ABC内角平分线的交点,I是△ABC外角平分线的交点,则∠O与∠I的数量关系是 .?
图7-X-12
16.如图7-X-13,在△ABC中,∠B=65°,∠BAD=40°,∠AED=100°,∠CDE=45°,求∠CAD的度数.
图7-X-13
类型之六 多边形的内角和与外角和
17.[2019·泰州]
八边形的内角和为 °.?
18.[2019·淮安]
若一个多边形的内角和为540°,则该多边形的边数是 .?
19.[2020·无锡滨湖区模拟]
已知一个多边形的内角和与外角和之比是3∶2,则这个多边形的边数为 .?
20.已知n边形的内角和θ=(n-2)·180°.
(1)甲同学说,θ能取900°,而乙同学说,θ也能取800°.甲、乙的说法对吗?若对,求出边数n;若不对,说明理由.
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
1.B
2.128 [解析]
如图,延长DC到点E,由题意可得∠ABC=∠BCE=∠BCA=26°,则∠ACD=180°-26°-26°=128°.
3.解:因为∠A=∠1,所以AE∥BF,所以∠E=∠EGF.因为CE∥DF,所以∠EGF=∠F,所以∠E=∠F.
4.A [解析]
由题意知∠E=45°,∠B=30°.因为DE∥BC,所以∠BCF=∠E=45°.
在△CFB中,∠BFC=180°-∠B-∠BCF=180°-30°-45°=105°.故选A.
5.80 [解析]
因为DE∥AF,所以∠BDE=∠FAD.因为∠CAF=20°,∠BAC=90°,所以∠FAD=70°,所以∠BDE=70°,则∠BED=180°-∠B-∠BDE=180°-30°-70°=80°.
6.B [解析]
由四边形EFGH是由四边形ABCD平移得到的,可知EH是AD的对应边,∠F是∠B的对应角.因为AD=5,∠B=70°,所以EH=5,∠F=70°.故选B.
7.B [解析]
由题意知BE=BC-EC=6-2=4,故平移的距离为4.故选B.
8.540 [解析]
把“之”字路平移到长方形地块的最上边和最左边,则余下部分是长方形,根据长方形的面积公式即可求出结果.
9.解:(1)略.
(2)平行且相等
10.B [解析]
由题意可得,3-2因为x为正整数,所以x可取2,3,4,
所以这样的三角形的个数为3.故选B.
11.7 [解析]
因为a,b满足|a-7|+(b-1)2=0,所以a-7=0,b-1=0,解得a=7,b=1.因为7-1=6,7+1=8,所以612.解:(1)第三条边长为30-a-(2a+2)=(28-3a)m.
(2)第一条边长不可以为7
m.理由:当a=7时,三边长分别为7
m,16
m,7
m.因为7+7<16,
所以7
m,7
m,16
m不能构成三角形,即第一条边长不可以为7
m.
13.A [解析]
由折叠的性质知∠A'=∠A=70°.
因为∠A+∠AED+∠ADE=∠A'+∠A'ED+∠A'DE=180°,
所以∠A+∠AED+∠ADE+∠A'+∠A'ED+∠A'DE=360°.
因为∠1+∠AED+∠A'ED=∠2+∠ADE+∠A'DE=180°,所以∠1+∠AED+∠A'ED+∠2+∠ADE+∠A'DE=360°,所以∠1+∠2=∠A+∠A'=2∠A=140°.故选A.
14.110 [解析]
因为∠A=40°,所以∠ACB+∠ABC=180°-40°=140°.又因为∠ACB=∠ABC,所以∠ACB=70°.
因为∠ACP=∠PBC,所以∠PBC+∠PCB=∠ACP+∠PCB=70°,
所以∠BPC=180°-70°=110°.
15.∠O+∠I=180° [解析]
如图,
因为O是△ABC内角平分线的交点,I是△ABC外角平分线的交点,
所以∠OBI=∠OBC+∠CBI=∠ABC+∠CBF=(∠ABC+∠CBF)=90°.
同法可证:∠OCI=90°.在四边形BOCI中,
因为∠O+∠OBI+∠I+∠OCI=360°,
所以∠O+∠I=360°-(∠OBI+∠OCI)=180°.
故答案为∠O+∠I=180°.
16.解:在△ABD中,因为∠B=65°,∠BAD=40°,
所以∠BDA=180°-(∠B+∠BAD)=180°-(65°+40°)=75°.
因为∠CDE=45°,所以∠ADE=180°-(∠BDA+∠CDE)=180°-(75°+45°)=60°.
在△ADE中,
因为∠AED=100°,所以∠CAD=180°-∠ADE-∠AED=180°-60°-100°=20°.
17.1080 [解析]
八边形的内角和为(8-2)×180°=1080°.
18.5
19.5 [解析]
设这个多边形的边数为n.依题意得(n-2)·180°=×360°,解得n=5.
故这个多边形的边数为5.
20.解:(1)甲的说法对,乙的说法不对.理由如下:因为当θ取900°时,900°=(n-2)·180°,解得n=7;当θ取800°时,800°=(n-2)·180°,解得n=.因为n为整数,所以θ不能取800°.
(2)依题意,得(n-2)·180°+540°=(n+x-2)·180°,解得x=3.故x的值为3.
类型之一 平行线的判定和性质
1.如图7-X-1,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1的度数为
( )
图7-X-1
A.30°
B.40°
C.50°
D.60°
2.[2019·扬州]
将一张长方形纸片折叠成如图7-X-2所示的图形,若∠ABC=26°,则∠ACD= °.?
图7-X-2
3.[2019·武汉]
如图7-X-3,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF.试说明:∠E=∠F.
图7-X-3
类型之二 平行线与三角形的综合运用
4.[2019·宿迁]
一副三角尺按图7-X-4所示摆放(直角顶点C重合),边AB与CE交于点F,DE∥BC,则∠BFC的度数为
( )
图7-X-4
A.105°
B.100°
C.75°
D.60°
5.如图7-X-5,△ABC是一块三角尺,∠BAC=90°,∠B=30°,现将三角尺叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED= °.?
图7-X-5
类型之三 平移
6.[2019·徐州铜山区期中]
如图7-X-6,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则
( )
图7-X-6
A.FG=5,∠G=70°
B.EH=5,∠F=70°
C.EF=5,∠F=70°
D.EF=5,∠E=70°
7.[2019·柳州期末]
如图7-X-7,△ABC沿着BC方向平移到△DEF,已知BC=6,EC=2,那么平移的距离为
( )
图7-X-7
A.2
B.4
C.6
D.8
8.如图7-X-8所示,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的“之”字路(图中阴影部分),余下部分绿化,道路的宽为2
m,则绿化的面积为 m2.?
图7-X-8
9.[2020·镇江京口区月考]
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图7-X-9所示,现将△ABC平移,使点A移动到点A'处,点B',C'分别是B,C的对应点.
(1)请画出平移后的△A'B'C';
(2)若连接AA',CC',则这两条线段之间的关系是 .?
图7-X-9
类型之四 三角形的三边关系
10.[2020·福建模拟]
若三角形的三边长分别为2,x,3,且x为正整数,则这样的三角形的个数为
( )
A.2
B.3
C.4
D.5
11.已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c= .?
12.小王准备用一段长30
m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为a
m,由于受地势限制,第二条边长只能是第一条边长的2倍多2
m.
(1)请用含a的式子表示第三条边长;
(2)第一条边长可以为7
m吗?请说明理由.
类型之五 三角形的内角和
13.如图7-X-10,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,点A与点A'重合.若∠A=70°,则∠1+∠2等于
( )
图7-X-10
A.140°
B.210°
C.110°
D.70°
14.[2019·盐城阜宁县模拟]
如图7-X-11,在△ABC中,∠ABC=∠ACB,∠A=40°,P是△ABC内一点,且∠ACP=∠PBC,则∠BPC= °.?
图7-X-11
15.[2019·南通期中]
如图7-X-12,O是△ABC内角平分线的交点,I是△ABC外角平分线的交点,则∠O与∠I的数量关系是 .?
图7-X-12
16.如图7-X-13,在△ABC中,∠B=65°,∠BAD=40°,∠AED=100°,∠CDE=45°,求∠CAD的度数.
图7-X-13
类型之六 多边形的内角和与外角和
17.[2019·泰州]
八边形的内角和为 °.?
18.[2019·淮安]
若一个多边形的内角和为540°,则该多边形的边数是 .?
19.[2020·无锡滨湖区模拟]
已知一个多边形的内角和与外角和之比是3∶2,则这个多边形的边数为 .?
20.已知n边形的内角和θ=(n-2)·180°.
(1)甲同学说,θ能取900°,而乙同学说,θ也能取800°.甲、乙的说法对吗?若对,求出边数n;若不对,说明理由.
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
1.B
2.128 [解析]
如图,延长DC到点E,由题意可得∠ABC=∠BCE=∠BCA=26°,则∠ACD=180°-26°-26°=128°.
3.解:因为∠A=∠1,所以AE∥BF,所以∠E=∠EGF.因为CE∥DF,所以∠EGF=∠F,所以∠E=∠F.
4.A [解析]
由题意知∠E=45°,∠B=30°.因为DE∥BC,所以∠BCF=∠E=45°.
在△CFB中,∠BFC=180°-∠B-∠BCF=180°-30°-45°=105°.故选A.
5.80 [解析]
因为DE∥AF,所以∠BDE=∠FAD.因为∠CAF=20°,∠BAC=90°,所以∠FAD=70°,所以∠BDE=70°,则∠BED=180°-∠B-∠BDE=180°-30°-70°=80°.
6.B [解析]
由四边形EFGH是由四边形ABCD平移得到的,可知EH是AD的对应边,∠F是∠B的对应角.因为AD=5,∠B=70°,所以EH=5,∠F=70°.故选B.
7.B [解析]
由题意知BE=BC-EC=6-2=4,故平移的距离为4.故选B.
8.540 [解析]
把“之”字路平移到长方形地块的最上边和最左边,则余下部分是长方形,根据长方形的面积公式即可求出结果.
9.解:(1)略.
(2)平行且相等
10.B [解析]
由题意可得,3-2
所以这样的三角形的个数为3.故选B.
11.7 [解析]
因为a,b满足|a-7|+(b-1)2=0,所以a-7=0,b-1=0,解得a=7,b=1.因为7-1=6,7+1=8,所以6
(2)第一条边长不可以为7
m.理由:当a=7时,三边长分别为7
m,16
m,7
m.因为7+7<16,
所以7
m,7
m,16
m不能构成三角形,即第一条边长不可以为7
m.
13.A [解析]
由折叠的性质知∠A'=∠A=70°.
因为∠A+∠AED+∠ADE=∠A'+∠A'ED+∠A'DE=180°,
所以∠A+∠AED+∠ADE+∠A'+∠A'ED+∠A'DE=360°.
因为∠1+∠AED+∠A'ED=∠2+∠ADE+∠A'DE=180°,所以∠1+∠AED+∠A'ED+∠2+∠ADE+∠A'DE=360°,所以∠1+∠2=∠A+∠A'=2∠A=140°.故选A.
14.110 [解析]
因为∠A=40°,所以∠ACB+∠ABC=180°-40°=140°.又因为∠ACB=∠ABC,所以∠ACB=70°.
因为∠ACP=∠PBC,所以∠PBC+∠PCB=∠ACP+∠PCB=70°,
所以∠BPC=180°-70°=110°.
15.∠O+∠I=180° [解析]
如图,
因为O是△ABC内角平分线的交点,I是△ABC外角平分线的交点,
所以∠OBI=∠OBC+∠CBI=∠ABC+∠CBF=(∠ABC+∠CBF)=90°.
同法可证:∠OCI=90°.在四边形BOCI中,
因为∠O+∠OBI+∠I+∠OCI=360°,
所以∠O+∠I=360°-(∠OBI+∠OCI)=180°.
故答案为∠O+∠I=180°.
16.解:在△ABD中,因为∠B=65°,∠BAD=40°,
所以∠BDA=180°-(∠B+∠BAD)=180°-(65°+40°)=75°.
因为∠CDE=45°,所以∠ADE=180°-(∠BDA+∠CDE)=180°-(75°+45°)=60°.
在△ADE中,
因为∠AED=100°,所以∠CAD=180°-∠ADE-∠AED=180°-60°-100°=20°.
17.1080 [解析]
八边形的内角和为(8-2)×180°=1080°.
18.5
19.5 [解析]
设这个多边形的边数为n.依题意得(n-2)·180°=×360°,解得n=5.
故这个多边形的边数为5.
20.解:(1)甲的说法对,乙的说法不对.理由如下:因为当θ取900°时,900°=(n-2)·180°,解得n=7;当θ取800°时,800°=(n-2)·180°,解得n=.因为n为整数,所以θ不能取800°.
(2)依题意,得(n-2)·180°+540°=(n+x-2)·180°,解得x=3.故x的值为3.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
