7.2 坐标方法的简单应用 同步练习(含解析)
文档属性
| 名称 | 7.2 坐标方法的简单应用 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 08:29:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2021年七年级下册7.2《坐标方法的简单应用》同步练习
一.选择题
1.在平面直角坐标系中,将点P(﹣3,2)向左平移2个单位长度后得到的点的坐标为( )
A.(﹣5,2) B.(﹣3,﹣1) C.(﹣3,4) D.(﹣1,2)
2.在平面直角坐标系中,将点P(3,2)向上平移2个单位长度,得到的点的坐标是( )
A.(3,4) B.(1,2) C.(5,2) D.(3,0)
3.在平面直角坐标系内,将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是( )
A.(3,1) B.(3,3) C.(﹣1,1) D.(﹣1,3)
4.线段CD是由线段AB平移得到的,点A(3,﹣1)的对应点C的坐标是(﹣2,5),则点B(0,4)的对应点D的坐标是( )
A.(5,﹣7) B.(4,3) C.(﹣5,10) D.(﹣3,7)
5.在平面直角坐标系中,把点A(﹣2,2)平移到点A'(﹣5,2),其平移方法是( )
A.向上平移3个单位 B.向下平移3个单位
C.向左平移3个单位 D.向右平移3个单位
6.如图,雷达探测器发现了A,B,C,D,E,F六个目标.目标C,F的位置分别表示为C(6,120°),F(5,210°),按照此方法表示目标A,B,D,E的位置时,其中表示正确的是( )
A.(4,30°) B.(1,90°) C.( 4,240°) D.(3,60°)
7.如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(﹣1,﹣2),“炮”位于(﹣4,1),则“象”位于点( )
A.(1,2) B.(﹣2,1) C.(1,﹣2) D.(﹣1,﹣2)
8.如图是一轰炸机群的飞行队形示意图,若在图上建立平面直角坐标,使最后两架轰炸机分别位于点M(﹣1,1)和点N(﹣1,﹣3),则第一架轰炸机位于的点P的坐标是( )
A.(﹣1,﹣3) B.(3,﹣1) C.(﹣1,3) D.(3,0)
9.在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(﹣5,2)、N(1,﹣4),将线段MN向上移动3个单位,向左移动2个单位平移后,点M,N的对应坐标为( )
A.(﹣5,1),(0,﹣5) B.(﹣4,2),(1,﹣3)
C.(﹣7,5),(﹣1,﹣1) D.(﹣5,0),(1,﹣5)
10.如图,在平面直角坐标系中,从点P1(﹣2,0),P2(﹣2,﹣2),P3(2,﹣2),P4(2,2),P5(﹣4,2),P6(﹣4,﹣4),P7(4,﹣4),P8(4,4),P9(﹣6,4),…,依此扩展下去,则P2019的坐标为( )
A.(1010,﹣1010) B.(﹣1010,﹣1010)
C.(1010,1010) D.(﹣1012,1010)
二.填空题
11.如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(﹣2,2),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标是 .
12.若点P(2﹣m,﹣1),将P点向右平移2个单位长度后落在y轴上,则m= .
13.平面直角坐标系中,将点A(3,﹣2)向右平移2个单位长度,那么平移后对应的点A'的坐标是 .
14.如果将点A(﹣3,﹣2)向右移2个单位长度再向上平移3个单位长度单位得到点A1,那么点A1的坐标是 .
15.如图,动点P从(0,3)出发沿所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2021次碰到长方形的边时点P的坐标为 .
16.在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B所在象限为 .
三.解答题
17.这是一所学校的平面示意图,建立适当的平面直角坐标系,并用坐标表示校门、图书馆、教学楼、旗杆和实验楼的位置.
18.小明和爸爸、妈妈到白银水川湿地公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点、x轴及y轴.只知道长廊E的坐标为(4,﹣3)和农家乐B的坐标为(﹣5,3),请你帮他画出平面直角坐标系,并写出其他各点的坐标.
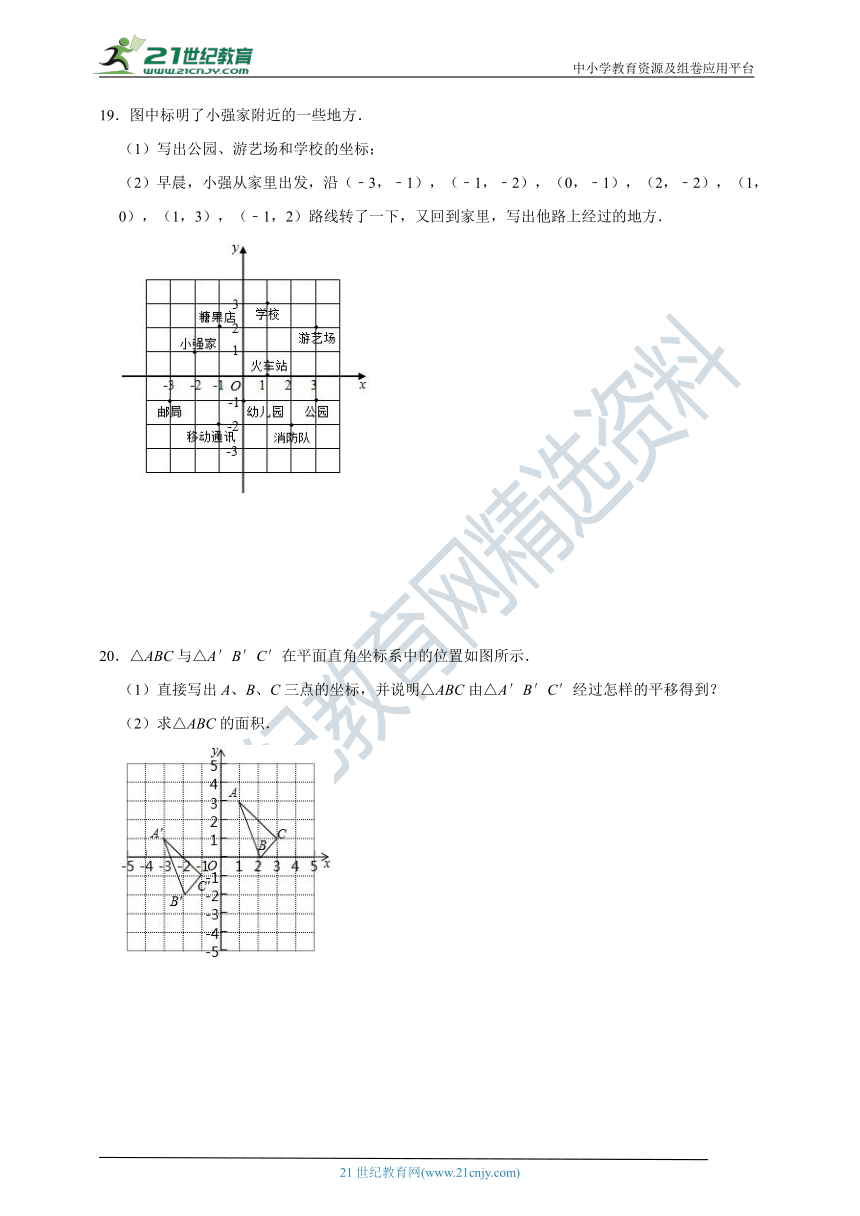
19.图中标明了小强家附近的一些地方.
(1)写出公园、游艺场和学校的坐标;
(2)早晨,小强从家里出发,沿(﹣3,﹣1),(﹣1,﹣2),(0,﹣1),(2,﹣2),(1,0),(1,3),(﹣1,2)路线转了一下,又回到家里,写出他路上经过的地方.
20.△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)直接写出A、B、C三点的坐标,并说明△ABC由△A′B′C′经过怎样的平移得到?
(2)求△ABC的面积.
21.如图,在平面直角坐标系中,已知A(﹣2,2),B(2,0),C(3,3),P(a,b)是三角形ABC的边AC上的一点,把三角形ABC经过平移后得三角形DEF,点P的对应点为P'(a﹣2,b﹣4).
(1)写出D,E,F三点的坐标;
(2)画出三角形DEF;
(3)求三角形DEF的面积.
22.如图,四边形ABCD各顶点的坐标分别为A(﹣3,﹣4)、B(0,﹣3)、C(﹣1,﹣1)、D(﹣3,﹣2).
(1)请画出将四边形ABCD先向右平移3个单位长度,再向上平移3个单位长度得到的四边形A′B′C′D′;
(2)写出点C′的坐标;
(3)如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,请求出这一平移的平移距离.
参考答案
一.选择题
1.【解答】解:将点P(﹣3,2)向左平移2个单位长度得到的点坐标为(﹣3﹣2,2),即(﹣5,2),
故选:A.
2.【解答】解:将点P(3,2)向上平移2个单位长度所得到的点坐标为(3,2+2),
即(3,4),
故选:A.
3.【解答】解:将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是(1+2,2﹣1),
即(3,1),
故选:A.
4.【解答】解:点A(3,﹣1)的对应点C的坐标是(﹣2,5),可知横坐标由3变为﹣2,向左移动了5个单位,﹣1变为5,表示向上移动了6个单位,
于是点B(0,4)的对应点D的横坐标为0﹣5=﹣5,点D的纵坐标为4+6=10,
故D(﹣5,10).
故选:C.
5.【解答】解:把点A(﹣2,2)平移到点A'(﹣5,2),其平移方法是向左平移3个单位,
故选:C.
6.【解答】解:由题意可知A、B、D、E的坐标可表示为:A(5,30°),故A选项错误;
B(2,90°),故B选项错误;
D(4,240°),故C选项正确;
E(3,300°),故D选项错误.
故选:C.
7.【解答】解:由“将”和“炮”的坐标可建立如图所示平面直角坐标系:
,
故“象”位于点(1,﹣2).
故选:C.
8.【解答】解:因为M(﹣1,1)和点N(﹣1,﹣3),所以可建立如下图所示平面直角坐标系:
所以可得点P的坐标为(3,﹣1),
故选:B.
9.【解答】解:∵线段MN向上移动3个单位,向左移动2个单位平移,
∴平移后M(﹣5,2)、N(1,﹣4)对应坐标为(﹣5﹣2,2+3)、(1﹣2,﹣4+3),
即(﹣7,5),(﹣1,﹣1).
故选:C.
10.【解答】解:由规律可得,2019÷4=504…3,
∴点P2019在第四象限,
∵点P3(2,﹣2),点P7(4,﹣4),点P11(6,﹣6),
∴点P2019(1010,﹣1010),
故选:A.
二.填空题
11.【解答】解:如图,
白棋(甲)的坐标是(2,1).
故答案为(2,1).
12.【解答】解:点P(2﹣m,﹣1),将P点向右平移2个单位长度后点的坐标为(4﹣m,﹣1),
∵向右平移2个单位长度后落在y轴上,
∴4﹣m=0,
解得:m=4,
故答案为:4.
13.【解答】解:根据题意,从点A平移到点A′,点A′的纵坐标不变,横坐标是3+2=5,
故点A′的坐标是(5,﹣2).
故答案为:(5,﹣2).
14.【解答】解:将点A(﹣3,﹣2)向右移2个单位长度再向上平移3个单位长度单位得到点A1,那么点A1的坐标是(﹣3+2,﹣2+3),即(﹣1,1).
故答案为(﹣1,1).
15.【解答】解:如图所示:经过6次反弹后动点回到出发点(0,3),
∵2021÷6=336…5,
∴当点P第2021次碰到矩形的边时为第337个循环组的第5次反弹,
∴点P的坐标为(1,4).
故答案为:(1,4).
16.【解答】解:点A(1,﹣2)向左平移2个单位,横坐标变为1﹣2=﹣1,向上平移3个单位,纵坐标变为﹣2+3=1,
所以所得点的坐标为(﹣1,1),在第二象限
故答案为:第二象限.
三.解答题
17.【解答】解:如图所示:校门(0,0)、图书馆(0,3)、教学楼(3,2)、旗杆(4,0)、实验楼(2,﹣3).
18.【解答】解:由题意可知,本题是以点D为坐标原点(0,0),DA为y轴的正半轴,建立平面直角坐标系.
则A、C、F的坐标分别为:A(0,4);C(﹣3,﹣2);F(5,5).
19.【解答】解:(1)公园(3,﹣1),游艺场(3,2),学校(1,3);
(2)邮局﹣﹣移动通讯﹣﹣幼儿园﹣﹣消防队﹣﹣火车站﹣﹣学校﹣﹣糖果店.
20.【解答】解:(1)A(1,3),B(2,0),C(3,1);△ABC由△A'B'C'先向右平移4个单位,再向上平移2个单位;或先向上平移2个单位,再向右平移4个单位;
(2)△ABC的面积=2×3﹣﹣﹣=2.
21.【解答】解:(1)D(﹣4,﹣2),E(0,﹣4),F(1,﹣1);
(2)如图所示:△DEF即为所求;
(3)S△DEF=5×3﹣×5×1﹣×4×2﹣×1×3
=15﹣2.5﹣4﹣1.5
=7.
22.【解答】解:(1)如图所示:四边形A′B′C′D′即为所求;
(2)点C′的坐标(2,2);
(3)平移距离:=3.
_21?????????è?????(www.21cnjy.com)_
2021年七年级下册7.2《坐标方法的简单应用》同步练习
一.选择题
1.在平面直角坐标系中,将点P(﹣3,2)向左平移2个单位长度后得到的点的坐标为( )
A.(﹣5,2) B.(﹣3,﹣1) C.(﹣3,4) D.(﹣1,2)
2.在平面直角坐标系中,将点P(3,2)向上平移2个单位长度,得到的点的坐标是( )
A.(3,4) B.(1,2) C.(5,2) D.(3,0)
3.在平面直角坐标系内,将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是( )
A.(3,1) B.(3,3) C.(﹣1,1) D.(﹣1,3)
4.线段CD是由线段AB平移得到的,点A(3,﹣1)的对应点C的坐标是(﹣2,5),则点B(0,4)的对应点D的坐标是( )
A.(5,﹣7) B.(4,3) C.(﹣5,10) D.(﹣3,7)
5.在平面直角坐标系中,把点A(﹣2,2)平移到点A'(﹣5,2),其平移方法是( )
A.向上平移3个单位 B.向下平移3个单位
C.向左平移3个单位 D.向右平移3个单位
6.如图,雷达探测器发现了A,B,C,D,E,F六个目标.目标C,F的位置分别表示为C(6,120°),F(5,210°),按照此方法表示目标A,B,D,E的位置时,其中表示正确的是( )
A.(4,30°) B.(1,90°) C.( 4,240°) D.(3,60°)
7.如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(﹣1,﹣2),“炮”位于(﹣4,1),则“象”位于点( )
A.(1,2) B.(﹣2,1) C.(1,﹣2) D.(﹣1,﹣2)
8.如图是一轰炸机群的飞行队形示意图,若在图上建立平面直角坐标,使最后两架轰炸机分别位于点M(﹣1,1)和点N(﹣1,﹣3),则第一架轰炸机位于的点P的坐标是( )
A.(﹣1,﹣3) B.(3,﹣1) C.(﹣1,3) D.(3,0)
9.在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(﹣5,2)、N(1,﹣4),将线段MN向上移动3个单位,向左移动2个单位平移后,点M,N的对应坐标为( )
A.(﹣5,1),(0,﹣5) B.(﹣4,2),(1,﹣3)
C.(﹣7,5),(﹣1,﹣1) D.(﹣5,0),(1,﹣5)
10.如图,在平面直角坐标系中,从点P1(﹣2,0),P2(﹣2,﹣2),P3(2,﹣2),P4(2,2),P5(﹣4,2),P6(﹣4,﹣4),P7(4,﹣4),P8(4,4),P9(﹣6,4),…,依此扩展下去,则P2019的坐标为( )
A.(1010,﹣1010) B.(﹣1010,﹣1010)
C.(1010,1010) D.(﹣1012,1010)
二.填空题
11.如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(﹣2,2),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标是 .
12.若点P(2﹣m,﹣1),将P点向右平移2个单位长度后落在y轴上,则m= .
13.平面直角坐标系中,将点A(3,﹣2)向右平移2个单位长度,那么平移后对应的点A'的坐标是 .
14.如果将点A(﹣3,﹣2)向右移2个单位长度再向上平移3个单位长度单位得到点A1,那么点A1的坐标是 .
15.如图,动点P从(0,3)出发沿所示方向运动,每当碰到长方形的边时反弹,反弹时反射角等于入射角,当点P第2021次碰到长方形的边时点P的坐标为 .
16.在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B所在象限为 .
三.解答题
17.这是一所学校的平面示意图,建立适当的平面直角坐标系,并用坐标表示校门、图书馆、教学楼、旗杆和实验楼的位置.
18.小明和爸爸、妈妈到白银水川湿地公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点、x轴及y轴.只知道长廊E的坐标为(4,﹣3)和农家乐B的坐标为(﹣5,3),请你帮他画出平面直角坐标系,并写出其他各点的坐标.
19.图中标明了小强家附近的一些地方.
(1)写出公园、游艺场和学校的坐标;
(2)早晨,小强从家里出发,沿(﹣3,﹣1),(﹣1,﹣2),(0,﹣1),(2,﹣2),(1,0),(1,3),(﹣1,2)路线转了一下,又回到家里,写出他路上经过的地方.
20.△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)直接写出A、B、C三点的坐标,并说明△ABC由△A′B′C′经过怎样的平移得到?
(2)求△ABC的面积.
21.如图,在平面直角坐标系中,已知A(﹣2,2),B(2,0),C(3,3),P(a,b)是三角形ABC的边AC上的一点,把三角形ABC经过平移后得三角形DEF,点P的对应点为P'(a﹣2,b﹣4).
(1)写出D,E,F三点的坐标;
(2)画出三角形DEF;
(3)求三角形DEF的面积.
22.如图,四边形ABCD各顶点的坐标分别为A(﹣3,﹣4)、B(0,﹣3)、C(﹣1,﹣1)、D(﹣3,﹣2).
(1)请画出将四边形ABCD先向右平移3个单位长度,再向上平移3个单位长度得到的四边形A′B′C′D′;
(2)写出点C′的坐标;
(3)如果将四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的,请求出这一平移的平移距离.
参考答案
一.选择题
1.【解答】解:将点P(﹣3,2)向左平移2个单位长度得到的点坐标为(﹣3﹣2,2),即(﹣5,2),
故选:A.
2.【解答】解:将点P(3,2)向上平移2个单位长度所得到的点坐标为(3,2+2),
即(3,4),
故选:A.
3.【解答】解:将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是(1+2,2﹣1),
即(3,1),
故选:A.
4.【解答】解:点A(3,﹣1)的对应点C的坐标是(﹣2,5),可知横坐标由3变为﹣2,向左移动了5个单位,﹣1变为5,表示向上移动了6个单位,
于是点B(0,4)的对应点D的横坐标为0﹣5=﹣5,点D的纵坐标为4+6=10,
故D(﹣5,10).
故选:C.
5.【解答】解:把点A(﹣2,2)平移到点A'(﹣5,2),其平移方法是向左平移3个单位,
故选:C.
6.【解答】解:由题意可知A、B、D、E的坐标可表示为:A(5,30°),故A选项错误;
B(2,90°),故B选项错误;
D(4,240°),故C选项正确;
E(3,300°),故D选项错误.
故选:C.
7.【解答】解:由“将”和“炮”的坐标可建立如图所示平面直角坐标系:
,
故“象”位于点(1,﹣2).
故选:C.
8.【解答】解:因为M(﹣1,1)和点N(﹣1,﹣3),所以可建立如下图所示平面直角坐标系:
所以可得点P的坐标为(3,﹣1),
故选:B.
9.【解答】解:∵线段MN向上移动3个单位,向左移动2个单位平移,
∴平移后M(﹣5,2)、N(1,﹣4)对应坐标为(﹣5﹣2,2+3)、(1﹣2,﹣4+3),
即(﹣7,5),(﹣1,﹣1).
故选:C.
10.【解答】解:由规律可得,2019÷4=504…3,
∴点P2019在第四象限,
∵点P3(2,﹣2),点P7(4,﹣4),点P11(6,﹣6),
∴点P2019(1010,﹣1010),
故选:A.
二.填空题
11.【解答】解:如图,
白棋(甲)的坐标是(2,1).
故答案为(2,1).
12.【解答】解:点P(2﹣m,﹣1),将P点向右平移2个单位长度后点的坐标为(4﹣m,﹣1),
∵向右平移2个单位长度后落在y轴上,
∴4﹣m=0,
解得:m=4,
故答案为:4.
13.【解答】解:根据题意,从点A平移到点A′,点A′的纵坐标不变,横坐标是3+2=5,
故点A′的坐标是(5,﹣2).
故答案为:(5,﹣2).
14.【解答】解:将点A(﹣3,﹣2)向右移2个单位长度再向上平移3个单位长度单位得到点A1,那么点A1的坐标是(﹣3+2,﹣2+3),即(﹣1,1).
故答案为(﹣1,1).
15.【解答】解:如图所示:经过6次反弹后动点回到出发点(0,3),
∵2021÷6=336…5,
∴当点P第2021次碰到矩形的边时为第337个循环组的第5次反弹,
∴点P的坐标为(1,4).
故答案为:(1,4).
16.【解答】解:点A(1,﹣2)向左平移2个单位,横坐标变为1﹣2=﹣1,向上平移3个单位,纵坐标变为﹣2+3=1,
所以所得点的坐标为(﹣1,1),在第二象限
故答案为:第二象限.
三.解答题
17.【解答】解:如图所示:校门(0,0)、图书馆(0,3)、教学楼(3,2)、旗杆(4,0)、实验楼(2,﹣3).
18.【解答】解:由题意可知,本题是以点D为坐标原点(0,0),DA为y轴的正半轴,建立平面直角坐标系.
则A、C、F的坐标分别为:A(0,4);C(﹣3,﹣2);F(5,5).
19.【解答】解:(1)公园(3,﹣1),游艺场(3,2),学校(1,3);
(2)邮局﹣﹣移动通讯﹣﹣幼儿园﹣﹣消防队﹣﹣火车站﹣﹣学校﹣﹣糖果店.
20.【解答】解:(1)A(1,3),B(2,0),C(3,1);△ABC由△A'B'C'先向右平移4个单位,再向上平移2个单位;或先向上平移2个单位,再向右平移4个单位;
(2)△ABC的面积=2×3﹣﹣﹣=2.
21.【解答】解:(1)D(﹣4,﹣2),E(0,﹣4),F(1,﹣1);
(2)如图所示:△DEF即为所求;
(3)S△DEF=5×3﹣×5×1﹣×4×2﹣×1×3
=15﹣2.5﹣4﹣1.5
=7.
22.【解答】解:(1)如图所示:四边形A′B′C′D′即为所求;
(2)点C′的坐标(2,2);
(3)平移距离:=3.
_21?????????è?????(www.21cnjy.com)_
