1.1分类加法计数原理与分步乘法计数原理3-2020-2021学年人教A版高中数学选修2-3课件(共24张PPT)
文档属性
| 名称 | 1.1分类加法计数原理与分步乘法计数原理3-2020-2021学年人教A版高中数学选修2-3课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 639.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 09:47:30 | ||
图片预览





文档简介
(共24张PPT)
1.1
分类加法计数原理
与分步乘法计数原理
六、两个计数原理的综合应用:
应用两个计数原理应注意的问题
(1)分类要做到“__________”,分类后再对每一类进行计数,最后用分类加法计数原理求和,得到总数.
(2)分步要做到“__________”完成了所有步骤,恰好完成任务,当然步与步之间要相互独立.分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
不重不漏
步骤完整
分配问题
(1)4名同学选报跑步、跳高、跳远三个项目,每人报一项,共有多少种报名方法?
(2)4名同学争夺跑步、跳高、跳远三项冠军,共有多少种可能的结果?
变式:用0,1,…,9这十个数字,可以组成多少个:
(1)三位整数;
(2)无重复数字的三位整数;
(3)小于500的无重复数字的三位数?
组数问题
1、8张卡片上写着0,1,2,…,7共8个数字,取其中的三张卡片排放在一起,可组成多少个不同的三位数?
解析:先排放百位从1,2,…,7共7个数中选一个有7种选法;再排十位,从除去百位的数外,剩余的7个数(包括0)中选一个,有7种选法;最后排个位,从除前两步选出的数外,剩余的6个数中选一个,有6种选法.由分步乘法计数原理,共可以组成7×7×6=294(个)不同的三位数.
涂色问题
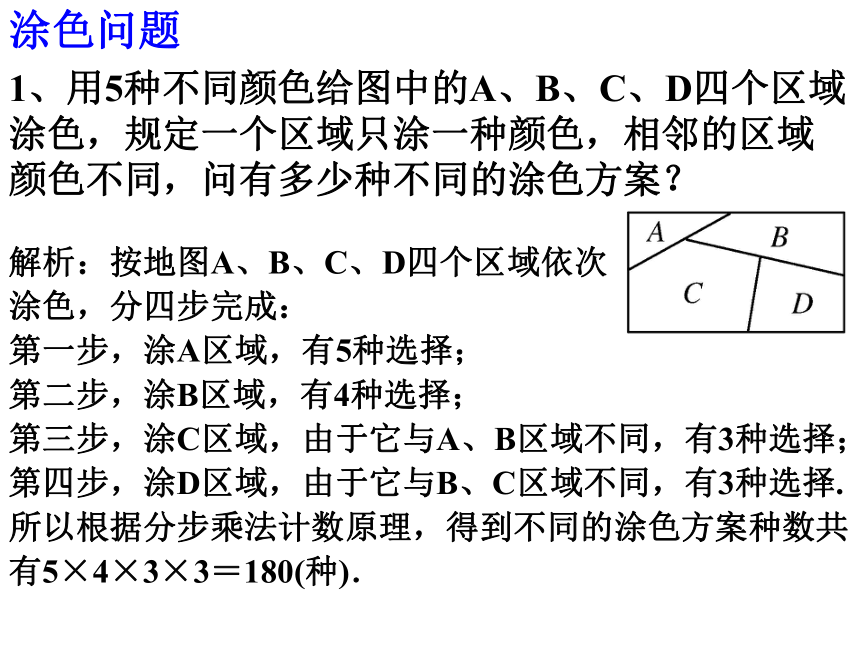
1、用5种不同颜色给图中的A、B、C、D四个区域涂色,规定一个区域只涂一种颜色,相邻的区域颜色不同,问有多少种不同的涂色方案?
解析:按地图A、B、C、D四个区域依次
涂色,分四步完成:
第一步,涂A区域,有5种选择;
第二步,涂B区域,有4种选择;
第三步,涂C区域,由于它与A、B区域不同,有3种选择;
第四步,涂D区域,由于它与B、C区域不同,有3种选择.
所以根据分步乘法计数原理,得到不同的涂色方案种数共有5×4×3×3=180(种).
2、用红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?
解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种.
因此应先分类后分步.
第一类,当B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法.
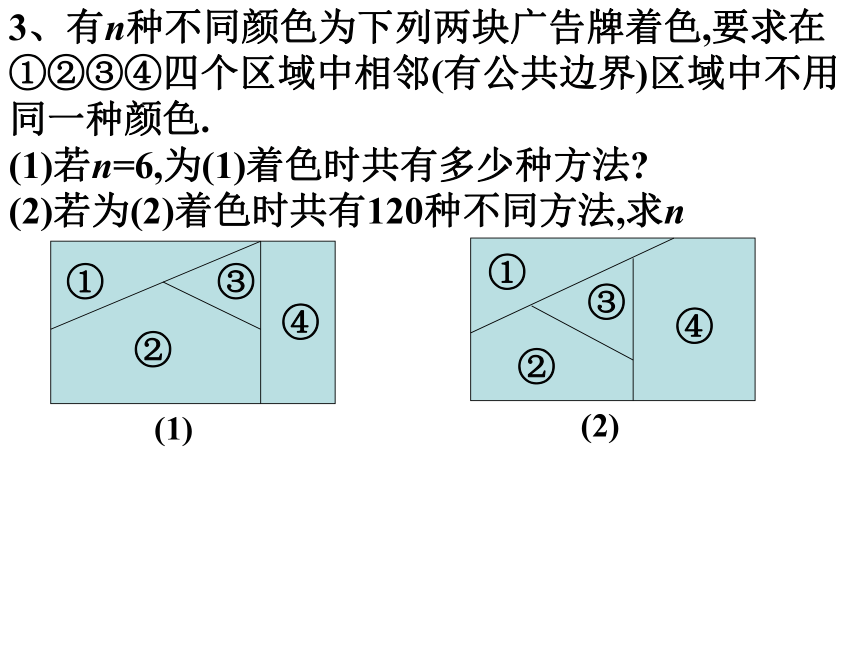
3、有n种不同颜色为下列两块广告牌着色,要求在①②③④四个区域中相邻(有公共边界)区域中不用同一种颜色.
(1)若n=6,为(1)着色时共有多少种方法?
(2)若为(2)着色时共有120种不同方法,求n
①
②
③
④
④
②
③
①
(1)
(2)
3×2
×1
×1
=6
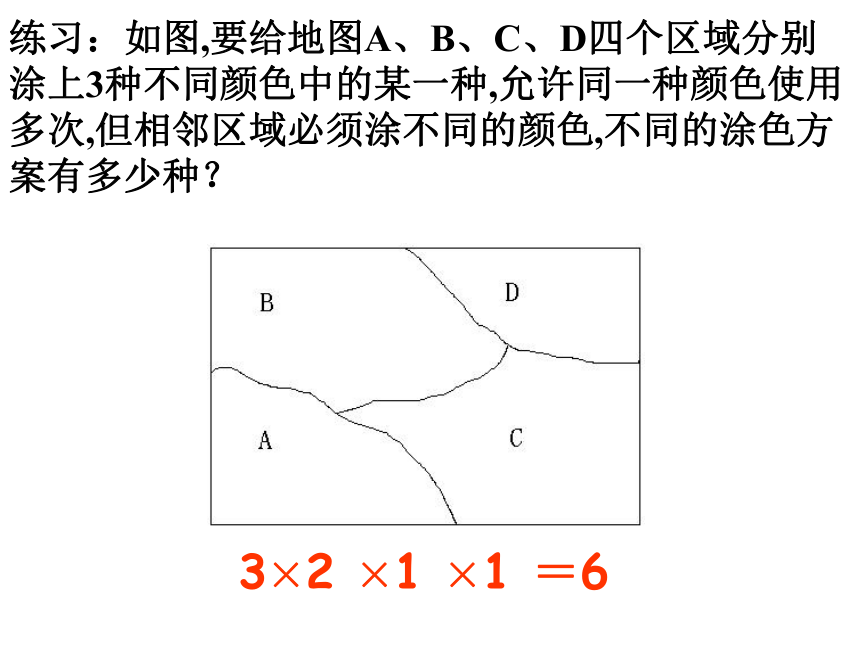
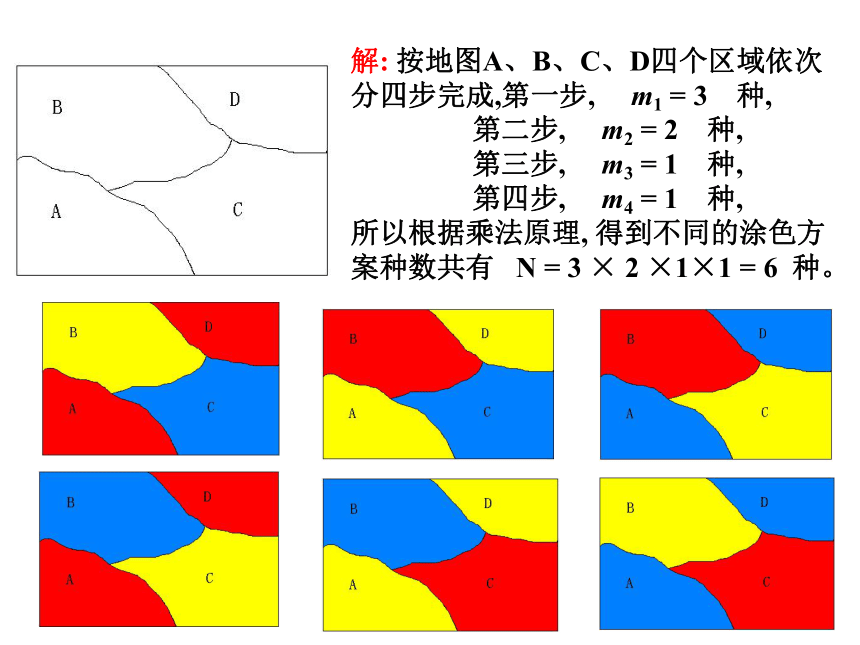
练习:如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
解:
按地图A、B、C、D四个区域依次分四步完成,第一步,
m1
=
3
种,
第二步,
m2
=
2
种,
第三步,
m3
=
1
种,
第四步,
m4
=
1
种,
所以根据乘法原理,
得到不同的涂色方案种数共有
N
=
3
×
2
×1×1
=
6
种。
4×3×2×2
=
48
若用4色,结果又怎样呢?
如图,要给A、B、C、D、E五个区域分别涂上4种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
A
B
C
D
E
4×3×2×1×1
=24
(1)B、D同色:
(2)B、D不同色:
+
72
=
×1×2
=48
4×3×2
种植问题
1、从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,求有多少种不同的种植方法.
方法一(直接法):若黄瓜种在第一块土地上,则有3×2×1=6种不同种植方法.
同理,黄瓜种在第二块、第三块土地上,均有3×2×1=6种.故不同的种植方法共有6×3=18种.
方法二(间接法):从4种蔬菜中选出3种,种在三块地上,有4×3×2=24种,其中不种黄瓜有3×2×1=6种,故共有不同种植方法24-6=18种.
2、如图,用6种不同的作物把图中A、B、C、D四块区域分开,若相邻区域不能种植同一种作物,则不同的种法共有( )
A.400种 B.460种
C.480种
D.496种
解析:从A开始,有6种方法,B有5种,C有4种,D、A种相同作物1种,D、A不同作物3种,
∴不同种法有6×5×4×(1+3)=480种.
故选C.
3、某城市在中心广场建造一个花圃,花圃分为6个部分(如右图)现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有______种.(以数字作答)
(1)②与④同色,则③⑤也同色或③⑥也同色,所以共有 N1=4×3×2×1×(1×1+1×1)=48种;
所以,共有N=N1+N2+N3=48+48+24=120种.
(2)②与⑤同色,则⑥③或⑥④同色,所以共有 N2=4×3×2×1×(1×1+1×1)=48种;
(3)③⑤且④⑥同色,则共N3=4×3×2×1×1×1=24种
解法一:从题意来看6部分种4种颜色的花,又从图形看,知必有2组同颜色的花,从同颜色的花入手分类求
小结
简单的选择问题
1、某校学生会由高一年级5人,高二年级6人,高三年级4人组成.
(1)选其中一人为学生会主席,有多少种不同的选法?
(2)若每年级选1人为校学生会常委成员,有多少种不同的选法?
(3)若要选出不同年级的两人分别参加市里组织的两项活动,有多少种不同的选法?
解:(1)分三类:第一类,从高一年级选一人,有5种选择;第二类,从高二年级选一人,有6种选择;第三类,从高三年级选一人,有4种选择.由分类加法计数原理,共有5+6+4=15(种)选法.
(2)分三步完成:第一步,从高一年级选一人,有5种选择;第二步,从高二年级选一人,有6种选择;第三步,从高三年级选一人,有4种选择.由分步乘法计数原理,共有5×6×4=120(种)选法.
(3)分三类:
高一、高二各一人,共有5×6=30(种)选法;
高一、高三各一人,共有5×4=20(种)选法;
高二、高三各一人,共有6×4=24(种)选法;
由分类加法计数原理,共有30+20+24=74(种)选法.
[题后感悟] 使用两个原理解题的本质
1、有4种不同的作物可供选择种植在如图所示的4块试验田中,每块种植一种作物,相邻的试验田(有公共边)不能种植同一种作物,共有多少种不同的种植方法?
练习
【错解】 第一步,种植A试验田有4种方法;
第二步,种植B试验田有3种方法;
第三步,种植C试验田有3种方法;
第四步,种植D试验田有2种方法;
由分步乘法计数原理知,共有N=4×3×3×2=72种种植方法.
【错因】 若按A、B、C、D的顺序依次种植作物,会导致D试验田的种植数受C试验田的影响,情况复杂.实际上种植C、D两块试验田再作为一步,用分类加法计数原理求解.
【正解】方法一:第一步,种植A试验田有4种方法;
第二步,种植B试验田有3种方法;
第三步,若C试验田种植的作物与B试验田相同,则D试验田有3种方法,此时有1×3=3种种植方法.
若C试验田种植的作物与B试验田不同,则C试验田有2种种植方法,D也有2种种植方法,共有2×2=4种种植方法.
由分类加法计数原理知,有3+4=7种方法.
第四步,由分步乘法计数原理有N=4×3×7=84种不同的种植方法.
方法二:(1)若A、D种植同种作物,则A、D有4种不同的种法,B有3种种植方法,C也有3种种植方法,由分步乘法计数原理,共有4×3×3=36种种植方法.
(2)若A、D种植不同作物,则A有4种种植方法,D有3种种植方法,B有2种种植方法,C有2种种植方法,由分步乘法计数原理,共有4×3×2×2=48种种植方法.
综上所述,由分类加法计数原理,共有N=36+48=84种种植方法.
2、由数字1,2,3,4,5,6可以组成没有重复数字的两位数的个数是( )
A.11 B.12
C.30
D.36
解析: 个位数字有6种选法,十位数字有5种选法,由分步乘法计数原理知,可组成6×5=30个无重复数字的两位数.
答案: C
3、如图,一环形花坛分成A、B、C、D四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为(
)
A.96
B.84
C.60
D.48
解析:方法一:先种A地有4种,再种B地有3种,
若C地与A地种相同的花,则C地有1种,D地有3种;
若C地与A地种不同花,则C地有2种,D地有2种,
即不同种法总数为N=4×3×(1×3+2×2)=84种.
方法二:若种4种花有4×3×2×1=24种;若种3种花,则A和C或B和D相同,有2×4×3×2=48种;若种2种花,则A和C相同且B和D相同,有4×3=12种.
共有N=24+48+12=84种.
答案: B
4、75600有多少个正约数?有多少个奇约数?
解:由于
75600=24×33×52×7
于是,要确定75600的一个约数,可分四步完成,即i,j,k,l分别在各自的范围内任取一个值,这样i有5种取法,j有4种取法,k有3种取法,l有2种取法,根据分步计数原理得约数的个数为5×4×3×2=120个.
(1)75600的每个约数都可以写成2i×3j×5k×7l的形式,其中0≤i≤4,0≤j≤3,0≤k≤2,0≤l≤1
(2)奇约数中不含有2的因数,因此75600的每个级约数都可以写成3j×5k×7l的形式,
所以奇约数的个数为4×3×2=24个
1.1
分类加法计数原理
与分步乘法计数原理
六、两个计数原理的综合应用:
应用两个计数原理应注意的问题
(1)分类要做到“__________”,分类后再对每一类进行计数,最后用分类加法计数原理求和,得到总数.
(2)分步要做到“__________”完成了所有步骤,恰好完成任务,当然步与步之间要相互独立.分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
不重不漏
步骤完整
分配问题
(1)4名同学选报跑步、跳高、跳远三个项目,每人报一项,共有多少种报名方法?
(2)4名同学争夺跑步、跳高、跳远三项冠军,共有多少种可能的结果?
变式:用0,1,…,9这十个数字,可以组成多少个:
(1)三位整数;
(2)无重复数字的三位整数;
(3)小于500的无重复数字的三位数?
组数问题
1、8张卡片上写着0,1,2,…,7共8个数字,取其中的三张卡片排放在一起,可组成多少个不同的三位数?
解析:先排放百位从1,2,…,7共7个数中选一个有7种选法;再排十位,从除去百位的数外,剩余的7个数(包括0)中选一个,有7种选法;最后排个位,从除前两步选出的数外,剩余的6个数中选一个,有6种选法.由分步乘法计数原理,共可以组成7×7×6=294(个)不同的三位数.
涂色问题
1、用5种不同颜色给图中的A、B、C、D四个区域涂色,规定一个区域只涂一种颜色,相邻的区域颜色不同,问有多少种不同的涂色方案?
解析:按地图A、B、C、D四个区域依次
涂色,分四步完成:
第一步,涂A区域,有5种选择;
第二步,涂B区域,有4种选择;
第三步,涂C区域,由于它与A、B区域不同,有3种选择;
第四步,涂D区域,由于它与B、C区域不同,有3种选择.
所以根据分步乘法计数原理,得到不同的涂色方案种数共有5×4×3×3=180(种).
2、用红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?
解析:给各区域标记号A、B、C、D、E,则A区域有4种不同的涂色方法,B区域有3种,C区域有2种,D区域有2种,但E区域的涂色依赖于B与D涂色的颜色,如果B与D颜色相同有2种,如果不相同,则只有一种.
因此应先分类后分步.
第一类,当B、D涂同色时,有4×3×2×1×2=48种,
第二类,当B、D不同色时,有4×3×2×1×1=24种,
故共有48+24=72种不同的涂色方法.
3、有n种不同颜色为下列两块广告牌着色,要求在①②③④四个区域中相邻(有公共边界)区域中不用同一种颜色.
(1)若n=6,为(1)着色时共有多少种方法?
(2)若为(2)着色时共有120种不同方法,求n
①
②
③
④
④
②
③
①
(1)
(2)
3×2
×1
×1
=6
练习:如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
解:
按地图A、B、C、D四个区域依次分四步完成,第一步,
m1
=
3
种,
第二步,
m2
=
2
种,
第三步,
m3
=
1
种,
第四步,
m4
=
1
种,
所以根据乘法原理,
得到不同的涂色方案种数共有
N
=
3
×
2
×1×1
=
6
种。
4×3×2×2
=
48
若用4色,结果又怎样呢?
如图,要给A、B、C、D、E五个区域分别涂上4种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
A
B
C
D
E
4×3×2×1×1
=24
(1)B、D同色:
(2)B、D不同色:
+
72
=
×1×2
=48
4×3×2
种植问题
1、从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,求有多少种不同的种植方法.
方法一(直接法):若黄瓜种在第一块土地上,则有3×2×1=6种不同种植方法.
同理,黄瓜种在第二块、第三块土地上,均有3×2×1=6种.故不同的种植方法共有6×3=18种.
方法二(间接法):从4种蔬菜中选出3种,种在三块地上,有4×3×2=24种,其中不种黄瓜有3×2×1=6种,故共有不同种植方法24-6=18种.
2、如图,用6种不同的作物把图中A、B、C、D四块区域分开,若相邻区域不能种植同一种作物,则不同的种法共有( )
A.400种 B.460种
C.480种
D.496种
解析:从A开始,有6种方法,B有5种,C有4种,D、A种相同作物1种,D、A不同作物3种,
∴不同种法有6×5×4×(1+3)=480种.
故选C.
3、某城市在中心广场建造一个花圃,花圃分为6个部分(如右图)现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有______种.(以数字作答)
(1)②与④同色,则③⑤也同色或③⑥也同色,所以共有 N1=4×3×2×1×(1×1+1×1)=48种;
所以,共有N=N1+N2+N3=48+48+24=120种.
(2)②与⑤同色,则⑥③或⑥④同色,所以共有 N2=4×3×2×1×(1×1+1×1)=48种;
(3)③⑤且④⑥同色,则共N3=4×3×2×1×1×1=24种
解法一:从题意来看6部分种4种颜色的花,又从图形看,知必有2组同颜色的花,从同颜色的花入手分类求
小结
简单的选择问题
1、某校学生会由高一年级5人,高二年级6人,高三年级4人组成.
(1)选其中一人为学生会主席,有多少种不同的选法?
(2)若每年级选1人为校学生会常委成员,有多少种不同的选法?
(3)若要选出不同年级的两人分别参加市里组织的两项活动,有多少种不同的选法?
解:(1)分三类:第一类,从高一年级选一人,有5种选择;第二类,从高二年级选一人,有6种选择;第三类,从高三年级选一人,有4种选择.由分类加法计数原理,共有5+6+4=15(种)选法.
(2)分三步完成:第一步,从高一年级选一人,有5种选择;第二步,从高二年级选一人,有6种选择;第三步,从高三年级选一人,有4种选择.由分步乘法计数原理,共有5×6×4=120(种)选法.
(3)分三类:
高一、高二各一人,共有5×6=30(种)选法;
高一、高三各一人,共有5×4=20(种)选法;
高二、高三各一人,共有6×4=24(种)选法;
由分类加法计数原理,共有30+20+24=74(种)选法.
[题后感悟] 使用两个原理解题的本质
1、有4种不同的作物可供选择种植在如图所示的4块试验田中,每块种植一种作物,相邻的试验田(有公共边)不能种植同一种作物,共有多少种不同的种植方法?
练习
【错解】 第一步,种植A试验田有4种方法;
第二步,种植B试验田有3种方法;
第三步,种植C试验田有3种方法;
第四步,种植D试验田有2种方法;
由分步乘法计数原理知,共有N=4×3×3×2=72种种植方法.
【错因】 若按A、B、C、D的顺序依次种植作物,会导致D试验田的种植数受C试验田的影响,情况复杂.实际上种植C、D两块试验田再作为一步,用分类加法计数原理求解.
【正解】方法一:第一步,种植A试验田有4种方法;
第二步,种植B试验田有3种方法;
第三步,若C试验田种植的作物与B试验田相同,则D试验田有3种方法,此时有1×3=3种种植方法.
若C试验田种植的作物与B试验田不同,则C试验田有2种种植方法,D也有2种种植方法,共有2×2=4种种植方法.
由分类加法计数原理知,有3+4=7种方法.
第四步,由分步乘法计数原理有N=4×3×7=84种不同的种植方法.
方法二:(1)若A、D种植同种作物,则A、D有4种不同的种法,B有3种种植方法,C也有3种种植方法,由分步乘法计数原理,共有4×3×3=36种种植方法.
(2)若A、D种植不同作物,则A有4种种植方法,D有3种种植方法,B有2种种植方法,C有2种种植方法,由分步乘法计数原理,共有4×3×2×2=48种种植方法.
综上所述,由分类加法计数原理,共有N=36+48=84种种植方法.
2、由数字1,2,3,4,5,6可以组成没有重复数字的两位数的个数是( )
A.11 B.12
C.30
D.36
解析: 个位数字有6种选法,十位数字有5种选法,由分步乘法计数原理知,可组成6×5=30个无重复数字的两位数.
答案: C
3、如图,一环形花坛分成A、B、C、D四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为(
)
A.96
B.84
C.60
D.48
解析:方法一:先种A地有4种,再种B地有3种,
若C地与A地种相同的花,则C地有1种,D地有3种;
若C地与A地种不同花,则C地有2种,D地有2种,
即不同种法总数为N=4×3×(1×3+2×2)=84种.
方法二:若种4种花有4×3×2×1=24种;若种3种花,则A和C或B和D相同,有2×4×3×2=48种;若种2种花,则A和C相同且B和D相同,有4×3=12种.
共有N=24+48+12=84种.
答案: B
4、75600有多少个正约数?有多少个奇约数?
解:由于
75600=24×33×52×7
于是,要确定75600的一个约数,可分四步完成,即i,j,k,l分别在各自的范围内任取一个值,这样i有5种取法,j有4种取法,k有3种取法,l有2种取法,根据分步计数原理得约数的个数为5×4×3×2=120个.
(1)75600的每个约数都可以写成2i×3j×5k×7l的形式,其中0≤i≤4,0≤j≤3,0≤k≤2,0≤l≤1
(2)奇约数中不含有2的因数,因此75600的每个级约数都可以写成3j×5k×7l的形式,
所以奇约数的个数为4×3×2=24个
