2020-2021学年高一数学人教A版必修二第一章1.2.2 空间几何体的三视图实用课件(共34张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修二第一章1.2.2 空间几何体的三视图实用课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 09:54:12 | ||
图片预览











文档简介
(共34张PPT)
题西林壁
苏轼
横看成岭侧成峰
远近高低各不同
不识庐山真面目
只缘身在此山中
猜猜他们是什么关系?
看问题不能只看单方面
几何体的正视图、侧视图和俯视图统称为几何体的三视图。
光线从几何体的前面向后面正投影,得到投影图,这种投影图叫做几何体的正视图
光线从几何体的上面向下面正投影,得到投影图,这种投影图叫做几何体的俯视图
光线从几何体的左面向右面正投影,得到投影图,这种投影图叫做几何体的侧视图
三视图的概念
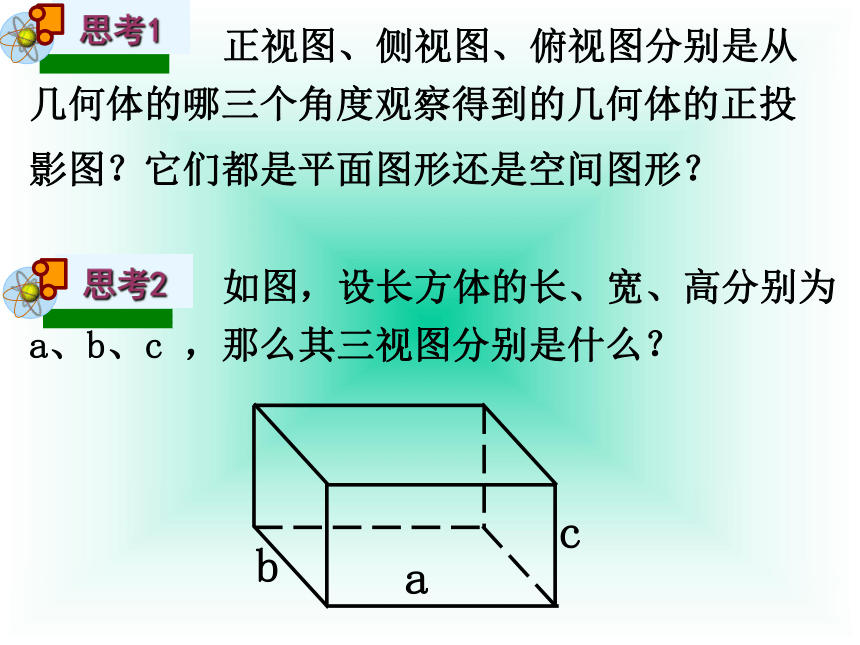
正视图、侧视图、俯视图分别是从几何体的哪三个角度观察得到的几何体的正投影图?它们都是平面图形还是空间图形?
思考1
如图,设长方体的长、宽、高分别为a、b、c
,那么其三视图分别是什么?
a
b
c
思考2
俯视图
正视图
俯视图
正视图
侧视图
侧视图
长度
高度
宽度
a
b
c
a
b
c
a
b
c
正视图是长为a高为c的矩形,
侧视图是宽为b高为c的矩形,
俯视图是长为a宽为b的矩形。
一般地,一个几何体的正视图、侧视图和俯视图的长度、宽度和高度有什么关系?
正视图
俯视图
侧视图
a
a
b
b
c
c
a
b
c
思考3
高平齐
宽相等
长对正,高平齐,宽相等
正俯一样长,
正侧一样高,
侧俯一样宽.
水立方:177m(长)×177m(宽)×31m(高)
正视图
俯视图
侧视图
31m
高
177m
长
177
m
宽
177m
宽
31m
高
177m
长
提问:正视图反映几何体的______________;侧视图反映几何体的_____________;
俯视图反映几何体的_______________。
长度和高度
宽度和高度
长度和宽度
水立方:
177m(长)×177m(宽)
×31m(高)
从前面正对着物体观察,画出正视图,正视图反映了物体的长和高及前后两个面的实形.
从上向下正对着物体观察,画出俯视图,布置在正视图的正下方,俯视图反映了物体的长和宽及上下两个面的实形.
三视图表达的意义
从左向右正对着物体观察,画出侧视图,布置在正视图的正右方,左视图反映了物体的宽和高及左右两个面的实形.
知识探究(一):画简单几何体的三视图
在简单组合体中,从正视、侧视、俯视等角度观察,有些轮廓线和棱能看见,有些轮廓线和棱不能看见,在画三视图时怎么处理?
思考4
观察下列圆柱,圆锥,球,圆台的图像,试画出它们的三视图。
画三视图
圆柱
正
侧
俯
圆柱的三视图
正视图
侧视图
俯视图
圆锥的三视图
圆
锥
侧视图
正视图
·
俯视图
能看见的轮廓线和棱用实线表示。
正视图
侧视图
俯视图
球的三视图
球
俯视图
正视图
侧视图
圆台的三视图
圆台
能看见的轮廓线和棱用实线表示。
俯视图
正视图
侧视图
圆台的三视图
圆台
不能看见的轮廓线和棱用虚线表示。
俯视图
正视图
侧视图
请画出正四棱锥的三视图
俯
侧
正
典例1
知识探究(一):画简单几何体的三视图
在简单组合体中,从正视、侧视、俯视等角度观察,有些轮廓线和棱能看见,有些轮廓线和棱不能看见,在画三视图时怎么处理?
思考4
画三视图的要求
(1)确定正视、侧视、俯视的方向
(2)位置:正视图
侧视图
俯视图
(3)大小:高平齐,长对正,宽相等
(4)能看见的轮廓线和棱用实线表示,不能看见的用虚线表示
请同学们试试画出立白洗洁精塑料瓶的三视图
思考5
正视图
侧视图
俯视图
下图所示的长方体和圆柱三视图是否正确?
侧视图
正视图
俯视图
正视图
侧视图
俯视图
理论迁移
知识探究(二):将三视图还原成几何体
一个空间几何体都对应一组三视图,若已知一个几何体的三视图,我们如何去想象这个几何体的原形结构,并画出其示意图呢?
下图分别是两个简单组合体的三视图,想象它们表示的组合体的结构特征,并画出其示意图.
思考6
侧视图
正视图
俯视图
正视图
侧视图
俯视图
正
侧
俯
直三棱柱
同一个几何体不同的放置其三视图也不相同。
正视图
侧视图
如图给出几何体的正,侧视图,
那么它除了是圆台外,还可能是什么几何体?
思考7
正视图
侧视图
正四棱台
俯
侧
正
俯视图
不同的几何体可能有某一两个视图相同,因此我们只有通过全部三个视图才能全面准确的还原一个几何体的特征。
学习过程
欣赏三视图
回忆学过的几何体的三视图
三视图的有关概念
画简单几何体的三视图
由三视图还原出简单几何体
小结:
画几何体的三视图时,能看得见的轮廓线
或棱用实线表示,不能看得见的轮廓线
或棱用虚线表示。
三视图之间的投影规律:
正视图与俯视图------长对正。
正视图与侧视图------高平齐。
俯视图与侧视图------宽相等。
1、
2、
3
、
空间想象能力,逆向思维能力。
通过几何体的三个视图能够全面准确的还原这个
几何体的特征。
作业:
P15练习:4.
P20习题1.2A组:1,2.
题西林壁
苏轼
横看成岭侧成峰
远近高低各不同
不识庐山真面目
只缘身在此山中
猜猜他们是什么关系?
看问题不能只看单方面
几何体的正视图、侧视图和俯视图统称为几何体的三视图。
光线从几何体的前面向后面正投影,得到投影图,这种投影图叫做几何体的正视图
光线从几何体的上面向下面正投影,得到投影图,这种投影图叫做几何体的俯视图
光线从几何体的左面向右面正投影,得到投影图,这种投影图叫做几何体的侧视图
三视图的概念
正视图、侧视图、俯视图分别是从几何体的哪三个角度观察得到的几何体的正投影图?它们都是平面图形还是空间图形?
思考1
如图,设长方体的长、宽、高分别为a、b、c
,那么其三视图分别是什么?
a
b
c
思考2
俯视图
正视图
俯视图
正视图
侧视图
侧视图
长度
高度
宽度
a
b
c
a
b
c
a
b
c
正视图是长为a高为c的矩形,
侧视图是宽为b高为c的矩形,
俯视图是长为a宽为b的矩形。
一般地,一个几何体的正视图、侧视图和俯视图的长度、宽度和高度有什么关系?
正视图
俯视图
侧视图
a
a
b
b
c
c
a
b
c
思考3
高平齐
宽相等
长对正,高平齐,宽相等
正俯一样长,
正侧一样高,
侧俯一样宽.
水立方:177m(长)×177m(宽)×31m(高)
正视图
俯视图
侧视图
31m
高
177m
长
177
m
宽
177m
宽
31m
高
177m
长
提问:正视图反映几何体的______________;侧视图反映几何体的_____________;
俯视图反映几何体的_______________。
长度和高度
宽度和高度
长度和宽度
水立方:
177m(长)×177m(宽)
×31m(高)
从前面正对着物体观察,画出正视图,正视图反映了物体的长和高及前后两个面的实形.
从上向下正对着物体观察,画出俯视图,布置在正视图的正下方,俯视图反映了物体的长和宽及上下两个面的实形.
三视图表达的意义
从左向右正对着物体观察,画出侧视图,布置在正视图的正右方,左视图反映了物体的宽和高及左右两个面的实形.
知识探究(一):画简单几何体的三视图
在简单组合体中,从正视、侧视、俯视等角度观察,有些轮廓线和棱能看见,有些轮廓线和棱不能看见,在画三视图时怎么处理?
思考4
观察下列圆柱,圆锥,球,圆台的图像,试画出它们的三视图。
画三视图
圆柱
正
侧
俯
圆柱的三视图
正视图
侧视图
俯视图
圆锥的三视图
圆
锥
侧视图
正视图
·
俯视图
能看见的轮廓线和棱用实线表示。
正视图
侧视图
俯视图
球的三视图
球
俯视图
正视图
侧视图
圆台的三视图
圆台
能看见的轮廓线和棱用实线表示。
俯视图
正视图
侧视图
圆台的三视图
圆台
不能看见的轮廓线和棱用虚线表示。
俯视图
正视图
侧视图
请画出正四棱锥的三视图
俯
侧
正
典例1
知识探究(一):画简单几何体的三视图
在简单组合体中,从正视、侧视、俯视等角度观察,有些轮廓线和棱能看见,有些轮廓线和棱不能看见,在画三视图时怎么处理?
思考4
画三视图的要求
(1)确定正视、侧视、俯视的方向
(2)位置:正视图
侧视图
俯视图
(3)大小:高平齐,长对正,宽相等
(4)能看见的轮廓线和棱用实线表示,不能看见的用虚线表示
请同学们试试画出立白洗洁精塑料瓶的三视图
思考5
正视图
侧视图
俯视图
下图所示的长方体和圆柱三视图是否正确?
侧视图
正视图
俯视图
正视图
侧视图
俯视图
理论迁移
知识探究(二):将三视图还原成几何体
一个空间几何体都对应一组三视图,若已知一个几何体的三视图,我们如何去想象这个几何体的原形结构,并画出其示意图呢?
下图分别是两个简单组合体的三视图,想象它们表示的组合体的结构特征,并画出其示意图.
思考6
侧视图
正视图
俯视图
正视图
侧视图
俯视图
正
侧
俯
直三棱柱
同一个几何体不同的放置其三视图也不相同。
正视图
侧视图
如图给出几何体的正,侧视图,
那么它除了是圆台外,还可能是什么几何体?
思考7
正视图
侧视图
正四棱台
俯
侧
正
俯视图
不同的几何体可能有某一两个视图相同,因此我们只有通过全部三个视图才能全面准确的还原一个几何体的特征。
学习过程
欣赏三视图
回忆学过的几何体的三视图
三视图的有关概念
画简单几何体的三视图
由三视图还原出简单几何体
小结:
画几何体的三视图时,能看得见的轮廓线
或棱用实线表示,不能看得见的轮廓线
或棱用虚线表示。
三视图之间的投影规律:
正视图与俯视图------长对正。
正视图与侧视图------高平齐。
俯视图与侧视图------宽相等。
1、
2、
3
、
空间想象能力,逆向思维能力。
通过几何体的三个视图能够全面准确的还原这个
几何体的特征。
作业:
P15练习:4.
P20习题1.2A组:1,2.
