第14章 三角形 单元测试-沪教版(上海)七年级数学第二学期(Word版含答案)
文档属性
| 名称 | 第14章 三角形 单元测试-沪教版(上海)七年级数学第二学期(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 417.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 07:52:23 | ||
图片预览



文档简介
第十四章 三角形 单元测试
一、单选题
1.三角形的两边长分别为false和false,则第三边长可能为( )
A.false B.false C.false D.false
2.在false中,若false,false,则false为()
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
3.如图,AC∥BD,AD与BC相交于O,∠AOB=75°,∠B=30°,那么∠A等于( )
A.75° B.60° C.45° D.30°
4.如图,已知false,若要使得false,则添加的一个条件不能是( )
A.false B.false
C.AB=DC D.AC=DB
5.如图,两个三角形全等,则false等于( )
A.false B.false C.false D.false
6.如图,将false绕点false顺时针旋转false得到false,点false、false、false在同一条直线上.若false,则false的度数是( )
A.false B.false C.false D.false
7.下列关于等边三角形的性质的叙述中,错误的是( )
A.是等腰三角形 B.三个角都相等 C.三条边都相等 D.只有一条对称轴
8.如图,在false中,false,false平分false,将false连续翻折两次,C点的对应点E点落在边false上,B点的对应点F点恰好落在边false上,则下列结论正确的是( )
A.false B.false
C.false D.false
9.如图,在false中,点D在边BC上,且满足false,过点D作false,交AC于点E.设false,false,false,则( )
A.false B.false
C.false D.false
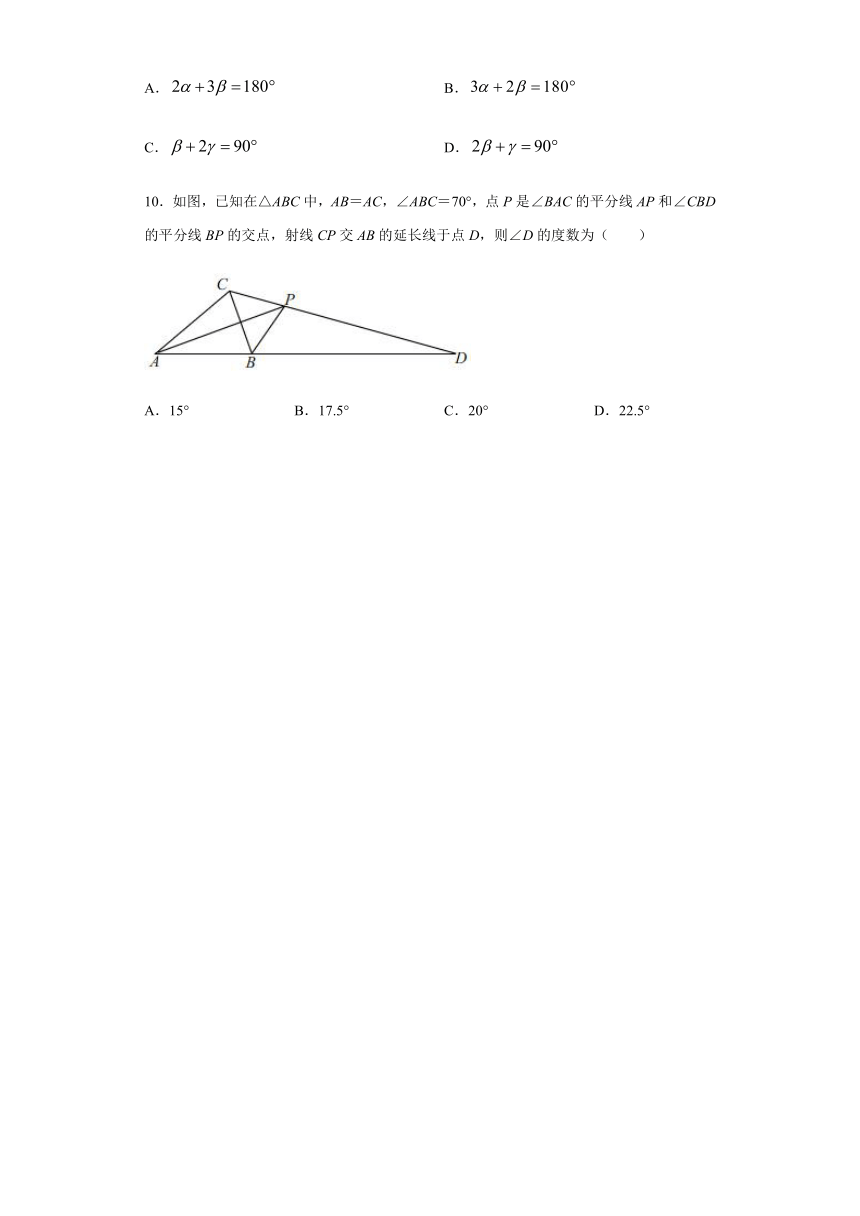
10.如图,已知在△ABC中,AB=AC,∠ABC=70°,点P是∠BAC的平分线AP和∠CBD的平分线BP的交点,射线CP交AB的延长线于点D,则∠D的度数为( )
A.15° B.17.5° C.20° D.22.5°
二、填空题
11.在falseABC中,∠A=false∠B=false∠C,则∠B=____度.
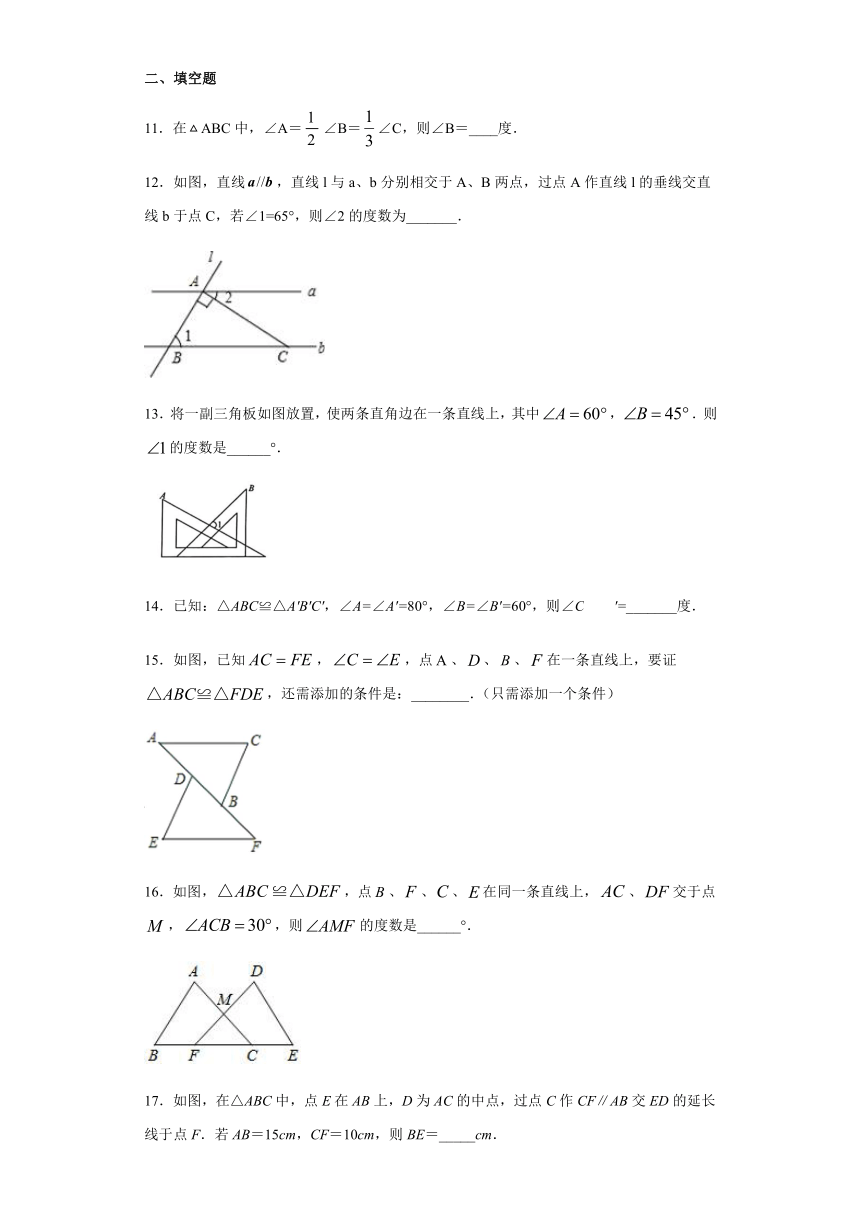
12.如图,直线false,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=65°,则∠2的度数为_______.
13.将一副三角板如图放置,使两条直角边在一条直线上,其中false,false.则false的度数是______°.
14.已知:△ABC≌△A′B′C′,∠A=∠A′=80°,∠B=∠B′=60°,则∠C′=_______度.
15.如图,已知false,false,点false、false、false、false在一条直线上,要证false,还需添加的条件是:________.(只需添加一个条件)
16.如图,false,点false、false、false、false在同一条直线上,false、false交于点false,false,则false的度数是______°.
17.如图,在△ABC中,点E在AB上,D为AC的中点,过点C作CF∥AB交ED的延长线于点F.若AB=15cm,CF=10cm,则BE=_____cm.
18.等腰三角形一腰上的高与另一腰的夹角为40°,则该等腰三角形的顶角的度数为_______.
19.如图,已知在false中,false为false上一点,且false为false上一点,且false,则false的度数是________.
20.如图,false是false的中线,E是false上一点,false交false于F,若false,则false__________.
三、解答题
21.如图,已知:AB=AC,BD=CD,点P是AD延长线上的一点.
求证:PB=PC.
22.如图,false交false于点D,false,false.
(1)求证:false;
(2)若false,求false的度数.
23.如图,四边形false中,false是对角线,false.
(1)求证:false;
(2)判断false的形状并说明.
24.如图所示,在△ABC中,∠B=∠C=50°,点D在边BC上运动,连接AD,作∠ADE=50°,且DE交AC边于点E.
(1)若AB=CD,求证:△ABD≌△DCE
(2)若点D在BC边上运动(点D不与点B,C重合),求出△ADE中为等腰三角形时∠CDE的度数.
25.已知false和false,AB=AD,false,false,AD与BC交与点P,点C在DE上.
(1)求证:BC=DE
(2)若false,false,
①求false的度数
②求证:CP=CE
26.已知:△ABC为等边三角形.
(1)如图1,点D、E分别为边BC、AC上的点,且BD=CE.
①求证:△ABD≌△BCE.
②求∠AFE的度数.
(2)如图2,点D为△ABC外一点,∠BDC=60°,BA、CD的延长线交于点E,连接AD,猜想线段AD、CD、BD之间的数量关系并加以证明.
(3)如图3,线段DB的长为3,线段DC的长为2,连接BC,以BC为边作等边△ABC,连接AD,直接写出当线段AD取最大值与最小值时∠BDC的度数.
参考答案
1.C
2.C
3.C
4.C
5.C
6.B
7.D
8.D
9.D
10.A
11.60
12.false
13.75
14.40°
15.false或false或false∥false(答案不唯一).
16.60
17.5
18.50°或130°.
19.45°
20.1.5
21.证明:在△ABD和△ACD中,
false,
∴△ABD≌△ACD,
∴∠BAP=∠CAP,
在△ABP和△ACP中,
false,
∴△ABP≌△ACP,
∴PB=PC.
22.(1)证明:在△DAC和△BDE中,
∠CAD+∠ADC+∠C=180°,
∠DBE+∠BDE+∠E=180°,
∵∠CAD=∠DBE,∠ADC=∠BDE,
∴∠C=∠E,
在△DAC和△BAE中,
false ,
∴△DAC≌△BAE,
∴DC=BE;
(2)设∠CAD=∠EAB=x,
则∠ADB=∠CAD+∠C=x+30°,
∵AB=AD,
∴∠ABD=∠ADB=x+30°,
在△ABD中,
∠ABD+∠ADB+∠BAE=180°,
即x+30°+x+30°+x=180°,解得:x=40°,
∴∠CDE=∠ADB=x+30°=70°.
23.证明:(1)在△ABC与△ADC中,
false,
∴△ABC≌△ADC(SAS);
(2)∵△ABC≌△ADC,
∴BC=DC,
∴△BCD是等腰三角形.
24.(1)证明:∵∠B=∠C=50°,∠ADE=50°,
∴∠B=∠ADE,
∵∠ADC=∠ADE+∠EDC,∠ADC =∠B+∠BAD,
∴∠BAD=∠EDC,
在△ABD和△DCE中,
false
∴△ABD≌△DCE(ASA);
(2)解:△ADE为等腰三角形,有以下三种可能:
①当AD=DE时,
∵∠ADE=50°,∠DAE=∠DEA=65°.
∵∠DEA=∠CDE+∠C,
∴∠CDE=∠DEA-∠C=65°-50°=15°;
②当DE=AE时,
∵∠ADE=50°,
∴∠DAE=∠ADE=50°,
∴∠DEC=∠ADE+∠DAE=100°,
∵∠C=50°,∴∠CDE=1880°-100°-50°=30°;
③当AD=AE时,
∵∠ADE=50°,
∴∠AED=∠ADE=50°,
∵∠AED=∠C+∠CDE=50°+∠CDE,
∴∠CDE=0°(不合题意,舍去);
综上所述,△ADE为等腰三角形时,∠CDE的度数为15°或30°.
25.解:(1)∵false,
∴false,
即∠BAC=∠DAE,
在△ABC和△ADE中
false ,
∴△ABC≌△ADE(ASA),
∴BC=DE;
(2)①∵false,false,
∴∠BAD=70°-30°=40°,
∴∠CAE=∠BAD=40°.
∵△ABC≌△ADE,
∴AC=AE,
∴∠E=∠ACE=false;
②∵false,∠E=∠ACE =70°,
∴∠APC=∠E=∠ACE =70°.
∵△ABC≌△ADE,
∴∠ACP=∠E =70°,
∴∠APC=∠E=∠ACE =∠ACP =70°.
在△ACP和△ACE中
false,
∴△ACP≌△ACE(AAS),
∴CP=CE.
26.(1)①证明:如图1中,∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
false ,
∴△ABD≌△BCE(SAS).
②解:如图1中,∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠AFE=∠FBA+∠BAD=∠FBA+∠CBE=∠CBA=60°.
(2)解:结论:BD=AD+DC.
理由:如图2中,在DB上取一点J,使得CJ=CD,
∵∠CDJ=60°,CJ=CD,
∴△CDJ是等边三角形,
∴∠JCD=∠ACB=60°,DJ=DC=CJ,
∴∠BCJ=∠ACD,
在△BCJ和△ACD中,
false ,
∴△BCJ≌△ACD(SAS),
∴BJ=AD,
∴BD=BJ+DJ=AD+DC.
(3)解:如图3中,以CD为边向外作等边△CDT,连接BT.
∵CT=CD,CB=CA,∠TCD=∠BCA=60°,
∴∠TCB=∠DCA,
在△TCB和△DCA中,
false ,
∴△TCB≌△DCA(SAS),
∴BT=AD,
∵CT=CD=2,BD=3,
∴3﹣2≤BT≤3+2,
∴1≤BT≤5,
∴1≤AD≤5.
∴AD的最小值为1,最大值为5.
当AD取最小值时,点T落在线段BD上,∠BDC=60°,当AD取最大值时,点T落在BD的延长线上,∠BDC=120°.
一、单选题
1.三角形的两边长分别为false和false,则第三边长可能为( )
A.false B.false C.false D.false
2.在false中,若false,false,则false为()
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
3.如图,AC∥BD,AD与BC相交于O,∠AOB=75°,∠B=30°,那么∠A等于( )
A.75° B.60° C.45° D.30°
4.如图,已知false,若要使得false,则添加的一个条件不能是( )
A.false B.false
C.AB=DC D.AC=DB
5.如图,两个三角形全等,则false等于( )
A.false B.false C.false D.false
6.如图,将false绕点false顺时针旋转false得到false,点false、false、false在同一条直线上.若false,则false的度数是( )
A.false B.false C.false D.false
7.下列关于等边三角形的性质的叙述中,错误的是( )
A.是等腰三角形 B.三个角都相等 C.三条边都相等 D.只有一条对称轴
8.如图,在false中,false,false平分false,将false连续翻折两次,C点的对应点E点落在边false上,B点的对应点F点恰好落在边false上,则下列结论正确的是( )
A.false B.false
C.false D.false
9.如图,在false中,点D在边BC上,且满足false,过点D作false,交AC于点E.设false,false,false,则( )
A.false B.false
C.false D.false
10.如图,已知在△ABC中,AB=AC,∠ABC=70°,点P是∠BAC的平分线AP和∠CBD的平分线BP的交点,射线CP交AB的延长线于点D,则∠D的度数为( )
A.15° B.17.5° C.20° D.22.5°
二、填空题
11.在falseABC中,∠A=false∠B=false∠C,则∠B=____度.
12.如图,直线false,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=65°,则∠2的度数为_______.
13.将一副三角板如图放置,使两条直角边在一条直线上,其中false,false.则false的度数是______°.
14.已知:△ABC≌△A′B′C′,∠A=∠A′=80°,∠B=∠B′=60°,则∠C′=_______度.
15.如图,已知false,false,点false、false、false、false在一条直线上,要证false,还需添加的条件是:________.(只需添加一个条件)
16.如图,false,点false、false、false、false在同一条直线上,false、false交于点false,false,则false的度数是______°.
17.如图,在△ABC中,点E在AB上,D为AC的中点,过点C作CF∥AB交ED的延长线于点F.若AB=15cm,CF=10cm,则BE=_____cm.
18.等腰三角形一腰上的高与另一腰的夹角为40°,则该等腰三角形的顶角的度数为_______.
19.如图,已知在false中,false为false上一点,且false为false上一点,且false,则false的度数是________.
20.如图,false是false的中线,E是false上一点,false交false于F,若false,则false__________.
三、解答题
21.如图,已知:AB=AC,BD=CD,点P是AD延长线上的一点.
求证:PB=PC.
22.如图,false交false于点D,false,false.
(1)求证:false;
(2)若false,求false的度数.
23.如图,四边形false中,false是对角线,false.
(1)求证:false;
(2)判断false的形状并说明.
24.如图所示,在△ABC中,∠B=∠C=50°,点D在边BC上运动,连接AD,作∠ADE=50°,且DE交AC边于点E.
(1)若AB=CD,求证:△ABD≌△DCE
(2)若点D在BC边上运动(点D不与点B,C重合),求出△ADE中为等腰三角形时∠CDE的度数.
25.已知false和false,AB=AD,false,false,AD与BC交与点P,点C在DE上.
(1)求证:BC=DE
(2)若false,false,
①求false的度数
②求证:CP=CE
26.已知:△ABC为等边三角形.
(1)如图1,点D、E分别为边BC、AC上的点,且BD=CE.
①求证:△ABD≌△BCE.
②求∠AFE的度数.
(2)如图2,点D为△ABC外一点,∠BDC=60°,BA、CD的延长线交于点E,连接AD,猜想线段AD、CD、BD之间的数量关系并加以证明.
(3)如图3,线段DB的长为3,线段DC的长为2,连接BC,以BC为边作等边△ABC,连接AD,直接写出当线段AD取最大值与最小值时∠BDC的度数.
参考答案
1.C
2.C
3.C
4.C
5.C
6.B
7.D
8.D
9.D
10.A
11.60
12.false
13.75
14.40°
15.false或false或false∥false(答案不唯一).
16.60
17.5
18.50°或130°.
19.45°
20.1.5
21.证明:在△ABD和△ACD中,
false,
∴△ABD≌△ACD,
∴∠BAP=∠CAP,
在△ABP和△ACP中,
false,
∴△ABP≌△ACP,
∴PB=PC.
22.(1)证明:在△DAC和△BDE中,
∠CAD+∠ADC+∠C=180°,
∠DBE+∠BDE+∠E=180°,
∵∠CAD=∠DBE,∠ADC=∠BDE,
∴∠C=∠E,
在△DAC和△BAE中,
false ,
∴△DAC≌△BAE,
∴DC=BE;
(2)设∠CAD=∠EAB=x,
则∠ADB=∠CAD+∠C=x+30°,
∵AB=AD,
∴∠ABD=∠ADB=x+30°,
在△ABD中,
∠ABD+∠ADB+∠BAE=180°,
即x+30°+x+30°+x=180°,解得:x=40°,
∴∠CDE=∠ADB=x+30°=70°.
23.证明:(1)在△ABC与△ADC中,
false,
∴△ABC≌△ADC(SAS);
(2)∵△ABC≌△ADC,
∴BC=DC,
∴△BCD是等腰三角形.
24.(1)证明:∵∠B=∠C=50°,∠ADE=50°,
∴∠B=∠ADE,
∵∠ADC=∠ADE+∠EDC,∠ADC =∠B+∠BAD,
∴∠BAD=∠EDC,
在△ABD和△DCE中,
false
∴△ABD≌△DCE(ASA);
(2)解:△ADE为等腰三角形,有以下三种可能:
①当AD=DE时,
∵∠ADE=50°,∠DAE=∠DEA=65°.
∵∠DEA=∠CDE+∠C,
∴∠CDE=∠DEA-∠C=65°-50°=15°;
②当DE=AE时,
∵∠ADE=50°,
∴∠DAE=∠ADE=50°,
∴∠DEC=∠ADE+∠DAE=100°,
∵∠C=50°,∴∠CDE=1880°-100°-50°=30°;
③当AD=AE时,
∵∠ADE=50°,
∴∠AED=∠ADE=50°,
∵∠AED=∠C+∠CDE=50°+∠CDE,
∴∠CDE=0°(不合题意,舍去);
综上所述,△ADE为等腰三角形时,∠CDE的度数为15°或30°.
25.解:(1)∵false,
∴false,
即∠BAC=∠DAE,
在△ABC和△ADE中
false ,
∴△ABC≌△ADE(ASA),
∴BC=DE;
(2)①∵false,false,
∴∠BAD=70°-30°=40°,
∴∠CAE=∠BAD=40°.
∵△ABC≌△ADE,
∴AC=AE,
∴∠E=∠ACE=false;
②∵false,∠E=∠ACE =70°,
∴∠APC=∠E=∠ACE =70°.
∵△ABC≌△ADE,
∴∠ACP=∠E =70°,
∴∠APC=∠E=∠ACE =∠ACP =70°.
在△ACP和△ACE中
false,
∴△ACP≌△ACE(AAS),
∴CP=CE.
26.(1)①证明:如图1中,∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中,
false ,
∴△ABD≌△BCE(SAS).
②解:如图1中,∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠AFE=∠FBA+∠BAD=∠FBA+∠CBE=∠CBA=60°.
(2)解:结论:BD=AD+DC.
理由:如图2中,在DB上取一点J,使得CJ=CD,
∵∠CDJ=60°,CJ=CD,
∴△CDJ是等边三角形,
∴∠JCD=∠ACB=60°,DJ=DC=CJ,
∴∠BCJ=∠ACD,
在△BCJ和△ACD中,
false ,
∴△BCJ≌△ACD(SAS),
∴BJ=AD,
∴BD=BJ+DJ=AD+DC.
(3)解:如图3中,以CD为边向外作等边△CDT,连接BT.
∵CT=CD,CB=CA,∠TCD=∠BCA=60°,
∴∠TCB=∠DCA,
在△TCB和△DCA中,
false ,
∴△TCB≌△DCA(SAS),
∴BT=AD,
∵CT=CD=2,BD=3,
∴3﹣2≤BT≤3+2,
∴1≤BT≤5,
∴1≤AD≤5.
∴AD的最小值为1,最大值为5.
当AD取最小值时,点T落在线段BD上,∠BDC=60°,当AD取最大值时,点T落在BD的延长线上,∠BDC=120°.
