_苏科版七年级下8[1].3同底数幂的除法(1)课件
文档属性
| 名称 | _苏科版七年级下8[1].3同底数幂的除法(1)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 462.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-23 00:00:00 | ||
图片预览


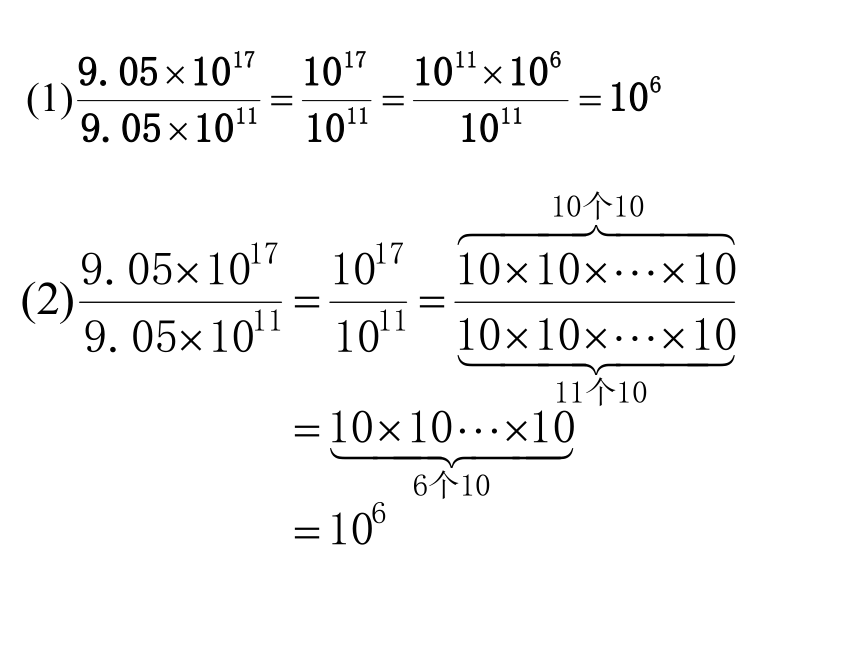
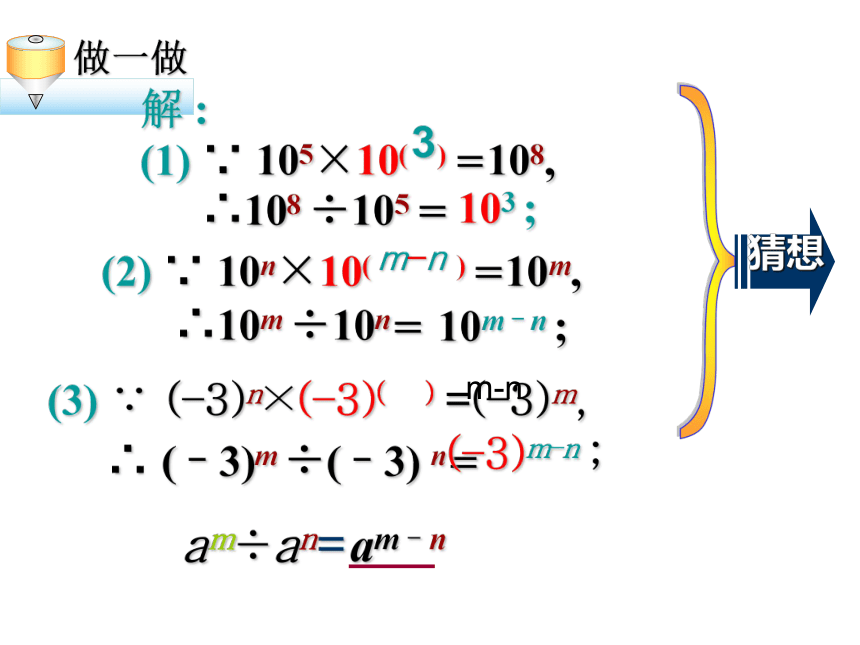

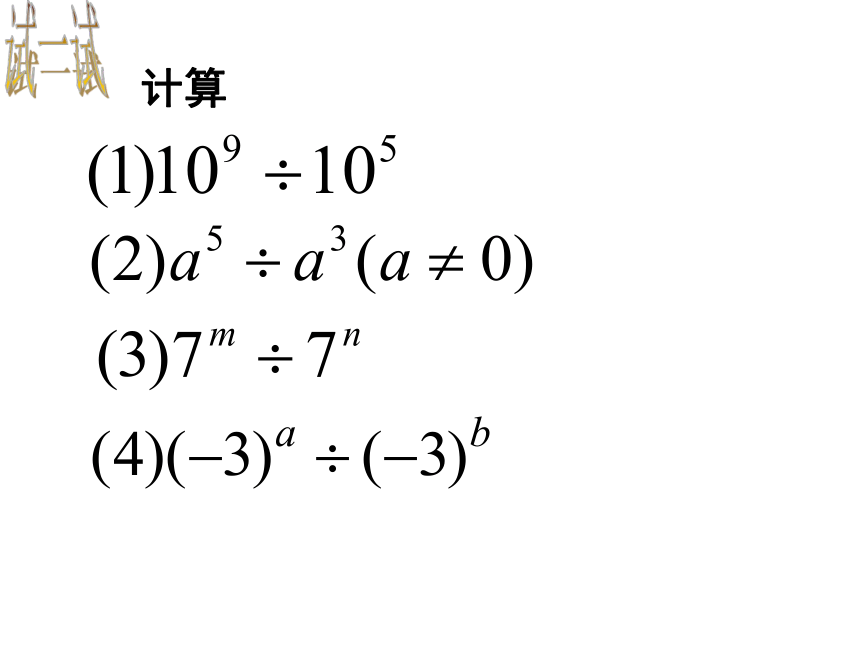
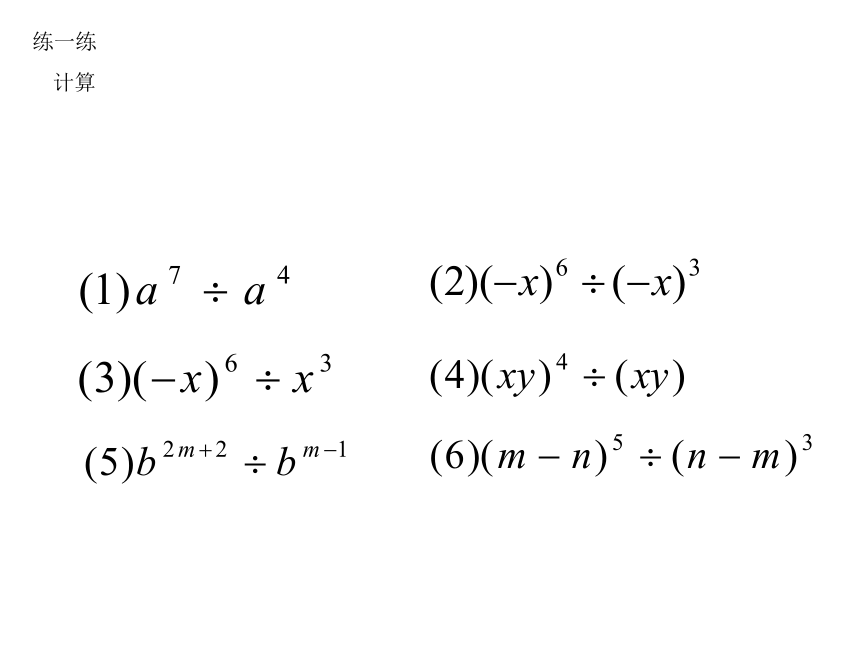
文档简介
(共19张PPT)
如果地球的体积大约是
太阳的体积大约为 。请问太阳的体积是地球体积的多少倍?
做一做
解 :
(1) ∵ 105×10( ) =108,
∴108 ÷105 =
103 ;
m–n
(2) ∵ 10n×10( ) =10m,
∴10m ÷10n=
10m–n ;
(3) ∵ (–3)n×(–3)( ) =(–3)m,
∴ (–3)m ÷(–3) n=
(–3)m–n ;
猜想
am–n
3
am÷an=
m-n
(a≠o, m,n都为正整数,且m﹥n)
同底数幂除法的运算性质:
计算
练一练
计算
同底数幂的 除法法则
am÷an= (a≠0, m、n都是正整数,且m>n)
同底数幂相除,底数_____, 指数______.
不变
相减
am–n
∴ am÷an=
证明: (法一) 用逆运算与同底的幂的乘法.
∵ an×a( ) =am,
m–n
am–n .
(法二) 用幂的定义:
am÷an=
个a
m
个a
n
个a
m–n
= am–n .
例题解析
计算:
(1) a7÷a4 ; (2) (-x)6÷(-x)3;
(3) (xy)4÷(xy) ; (4) b2m+2÷b2 .
= a7–4
= a3 ;
(1) a7÷a4
解:
(2) (-x)6÷(-x)3
= (-x)6–3
= (-x)3
(3) (xy)4÷(xy)
=(xy)4–1
(4) b2m+2÷b2
= b2m+2 – 2
阅读 体验
= -x3 ;
=(xy)3
=x3y3
= b2m .
例题解析
.
.
注意
最后结果中幂的形式应是最简的.
① 幂的指数、底数都应是最简的;
③ 幂的底数是积的形式时,要再用一次(ab)n=an an.
②底数中系数不能为负;
练 一 练:
计算:
1.m10÷(-m)4 2.(-b)9÷ (-b)6
3.(ab)8÷(-ab)2 4.t2m+3÷t2m-3(m为正整数)
(1)(x+y)6÷(x+y)5·(y+x)7
计算:
(5)(3y-2x)3·(2x-3y)2n+1÷(3y-2x)2n+2
(4)(m-n)9÷(n-m)8·(m-n)2
(3)(-a-b)5÷(a+b)
(2)(a-2)14÷(2-a)5
要细心哦 !!!
每一小题的底数均有不同,不能直接用同底数幂的法则,必须适当变形,使底数变为相同再计算。
(3)(-a-b)5÷(a+b)
=[-(a+b)]5÷(a+b)
=-(a+b)5÷(a+b)
=-(a+b)5-1
=-(a+b)4
(2)(a-2)14÷(2-a)5
=(2-a)14÷(2-a)5
=(2-a)14-5
=(2-a)9
(1)(x+y)6÷(x+y)5·(y+x)7
=(x+y)6÷(x+y)5(x+y)7
=(x+y)6-5+7
=(x+y)8
(4)(m-n)9÷(n-m)8·(m-n)2
=(m-n)9÷(m-n)8·(m-n)2
=(m-n)9-8+2
=(m-n)3
(5)(3y-2x)3·(2x-3y)2n+1÷(3y-2x)2n+2
=(3y-2x)3·[-(3y-2x)2n+1]÷(3y-2x)2n+2
=-(3y-2x)3+(2n+1)-(2n+2)
=-(3y-2x)2
1.若33·9m+4÷272m-1的值为729,求m的值。
拓展
本节课你的收获是什么?
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an =am+n
同底幂的除法运算法则:
am÷an=am–n (m,n为正整数)
.计算:
①a8÷a3÷a2
②(-x)n+3÷(-x)n+1
③(y3)4÷(y3·y2)2
④(a+b)3·(b+a)2÷(a+b)4
; ⑤ [(ab)4·(ab)5÷(ab)7]3
⑥[(m-n)8÷(n-m)6]·(m-n)3
⑦(a-b)5÷(b-a)3·(a-b)4
练一练
如果地球的体积大约是
太阳的体积大约为 。请问太阳的体积是地球体积的多少倍?
做一做
解 :
(1) ∵ 105×10( ) =108,
∴108 ÷105 =
103 ;
m–n
(2) ∵ 10n×10( ) =10m,
∴10m ÷10n=
10m–n ;
(3) ∵ (–3)n×(–3)( ) =(–3)m,
∴ (–3)m ÷(–3) n=
(–3)m–n ;
猜想
am–n
3
am÷an=
m-n
(a≠o, m,n都为正整数,且m﹥n)
同底数幂除法的运算性质:
计算
练一练
计算
同底数幂的 除法法则
am÷an= (a≠0, m、n都是正整数,且m>n)
同底数幂相除,底数_____, 指数______.
不变
相减
am–n
∴ am÷an=
证明: (法一) 用逆运算与同底的幂的乘法.
∵ an×a( ) =am,
m–n
am–n .
(法二) 用幂的定义:
am÷an=
个a
m
个a
n
个a
m–n
= am–n .
例题解析
计算:
(1) a7÷a4 ; (2) (-x)6÷(-x)3;
(3) (xy)4÷(xy) ; (4) b2m+2÷b2 .
= a7–4
= a3 ;
(1) a7÷a4
解:
(2) (-x)6÷(-x)3
= (-x)6–3
= (-x)3
(3) (xy)4÷(xy)
=(xy)4–1
(4) b2m+2÷b2
= b2m+2 – 2
阅读 体验
= -x3 ;
=(xy)3
=x3y3
= b2m .
例题解析
.
.
注意
最后结果中幂的形式应是最简的.
① 幂的指数、底数都应是最简的;
③ 幂的底数是积的形式时,要再用一次(ab)n=an an.
②底数中系数不能为负;
练 一 练:
计算:
1.m10÷(-m)4 2.(-b)9÷ (-b)6
3.(ab)8÷(-ab)2 4.t2m+3÷t2m-3(m为正整数)
(1)(x+y)6÷(x+y)5·(y+x)7
计算:
(5)(3y-2x)3·(2x-3y)2n+1÷(3y-2x)2n+2
(4)(m-n)9÷(n-m)8·(m-n)2
(3)(-a-b)5÷(a+b)
(2)(a-2)14÷(2-a)5
要细心哦 !!!
每一小题的底数均有不同,不能直接用同底数幂的法则,必须适当变形,使底数变为相同再计算。
(3)(-a-b)5÷(a+b)
=[-(a+b)]5÷(a+b)
=-(a+b)5÷(a+b)
=-(a+b)5-1
=-(a+b)4
(2)(a-2)14÷(2-a)5
=(2-a)14÷(2-a)5
=(2-a)14-5
=(2-a)9
(1)(x+y)6÷(x+y)5·(y+x)7
=(x+y)6÷(x+y)5(x+y)7
=(x+y)6-5+7
=(x+y)8
(4)(m-n)9÷(n-m)8·(m-n)2
=(m-n)9÷(m-n)8·(m-n)2
=(m-n)9-8+2
=(m-n)3
(5)(3y-2x)3·(2x-3y)2n+1÷(3y-2x)2n+2
=(3y-2x)3·[-(3y-2x)2n+1]÷(3y-2x)2n+2
=-(3y-2x)3+(2n+1)-(2n+2)
=-(3y-2x)2
1.若33·9m+4÷272m-1的值为729,求m的值。
拓展
本节课你的收获是什么?
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an =am+n
同底幂的除法运算法则:
am÷an=am–n (m,n为正整数)
.计算:
①a8÷a3÷a2
②(-x)n+3÷(-x)n+1
③(y3)4÷(y3·y2)2
④(a+b)3·(b+a)2÷(a+b)4
; ⑤ [(ab)4·(ab)5÷(ab)7]3
⑥[(m-n)8÷(n-m)6]·(m-n)3
⑦(a-b)5÷(b-a)3·(a-b)4
练一练
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
