七年级数学平行线的性质(第1课时课件)
文档属性
| 名称 | 七年级数学平行线的性质(第1课时课件) |

|
|
| 格式 | zip | ||
| 文件大小 | 909.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-23 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
a
c
b
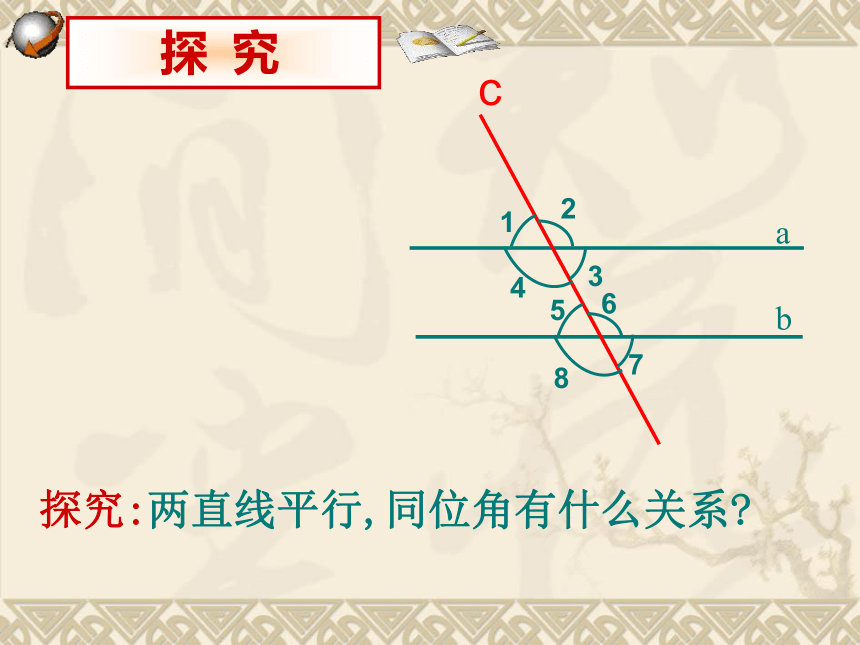
探究:两直线平行,同位角有什么关系
a
b
探 究
c
1
5
2
3
4
7
6
8
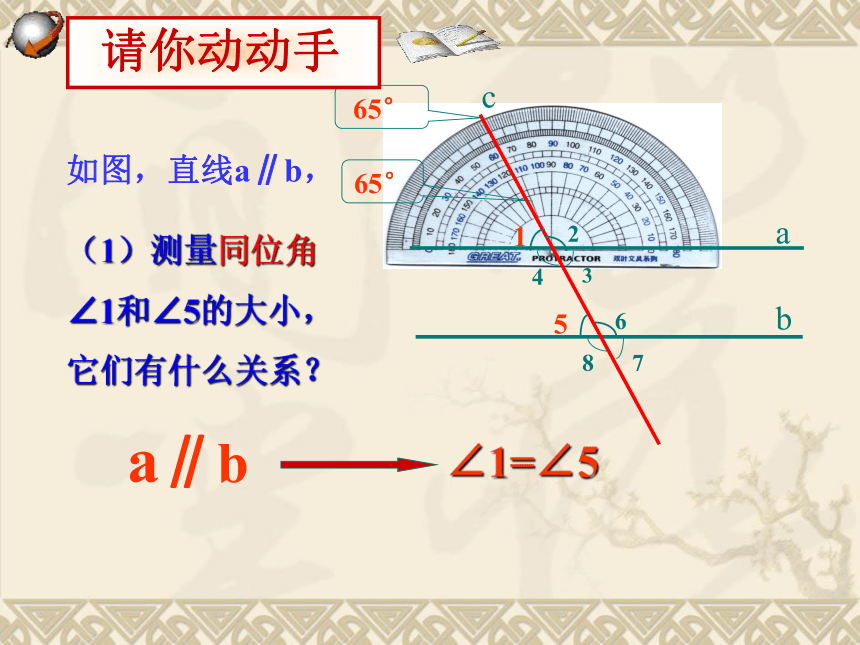
如图,直线a∥b,
(1)测量同位角∠1和∠5的大小,它们有什么关系?
65°
65°
c
a
b
1
5
2
4
3
6
8
7
∠1=∠5
a∥b
请你动动手
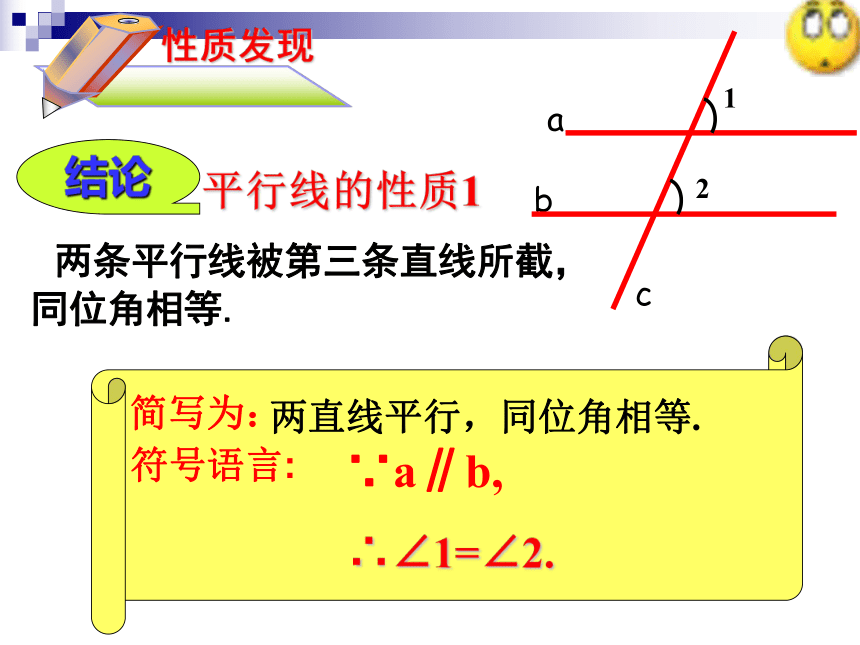
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
如图:已知a//b,那么 2与 3相等吗?
为什么
解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
合作交流二
b
1
2
a
c
3
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
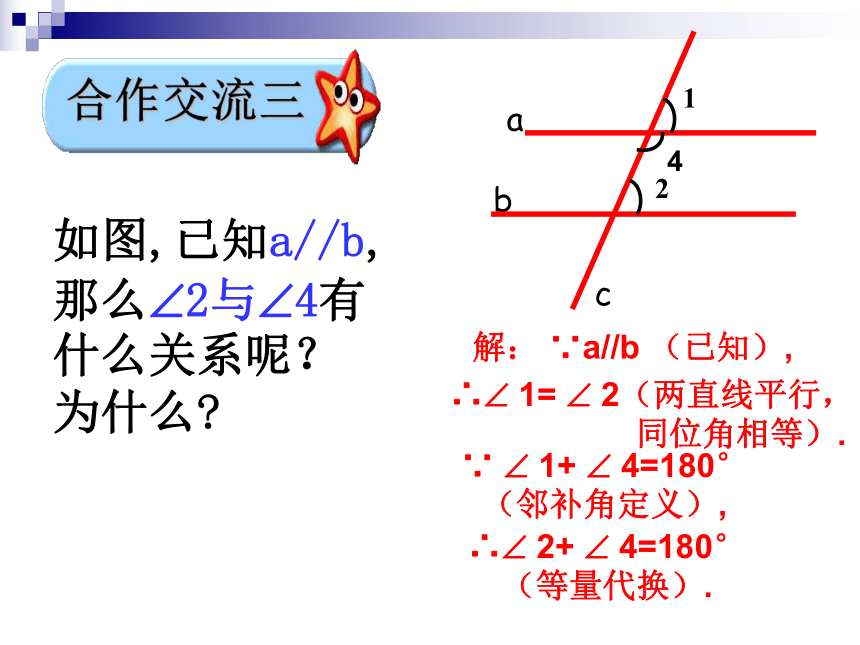
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流三
b
1
2
a
c
4
∴ 1= 2(两直线平行, 同位角相等).
∵ 1+ 4=180° (邻补角定义),
∴ 2+ 4=180° (等量代换).
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴ 2+ 4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
结论
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
例 如图所示是一块梯形铁片的残余部分,量得∠A=100 , ∠B=115°,梯形另外两个角各是多少度?
解决问题:
1、如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度
解:
∵ ∠2=∠1 (对顶角相等)
∴ ∠2=∠1 =54°
∵ a∥b(已知)
∴ ∠4=∠1=54°(两直线平行,同位角相等)
∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° - 54°=126°
即 ∠2=54° ,∠3=126°, ∠4=54°。
1
2
3
4
a
b
E
D
C
B
A
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
2、已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
(1)DE和BC平行吗?为什么?
(2) ∠C的度数是多少?
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度 为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
一、快速抢答
2
E
1
3
4
A
B
D
C
∠2=110o
∵两直线行,内错角相等
∠3=110o
∵两直线平行,同位角相等
∠4=70o
∵两直线平行,同旁内角互补
一、快速抢答
2、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
B
C
∠C=142o
∵两直线平行,内错角相等
一、快速抢答
3、如图直线 a ∥ b,直线b垂直于直线c,则直线a垂直于直线c吗
∟
∟
a
b
c
a⊥b
∵两直线平行, 同位角相等
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
判定
性质
平行线的性质和平行线的判定方法的 区 别 与 联 系
小结
a
c
b
探究:两直线平行,同位角有什么关系
a
b
探 究
c
1
5
2
3
4
7
6
8
如图,直线a∥b,
(1)测量同位角∠1和∠5的大小,它们有什么关系?
65°
65°
c
a
b
1
5
2
4
3
6
8
7
∠1=∠5
a∥b
请你动动手
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
如图:已知a//b,那么 2与 3相等吗?
为什么
解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
合作交流二
b
1
2
a
c
3
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流三
b
1
2
a
c
4
∴ 1= 2(两直线平行, 同位角相等).
∵ 1+ 4=180° (邻补角定义),
∴ 2+ 4=180° (等量代换).
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴ 2+ 4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
结论
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
例 如图所示是一块梯形铁片的残余部分,量得∠A=100 , ∠B=115°,梯形另外两个角各是多少度?
解决问题:
1、如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度
解:
∵ ∠2=∠1 (对顶角相等)
∴ ∠2=∠1 =54°
∵ a∥b(已知)
∴ ∠4=∠1=54°(两直线平行,同位角相等)
∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° - 54°=126°
即 ∠2=54° ,∠3=126°, ∠4=54°。
1
2
3
4
a
b
E
D
C
B
A
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
2、已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
(1)DE和BC平行吗?为什么?
(2) ∠C的度数是多少?
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度 为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
一、快速抢答
2
E
1
3
4
A
B
D
C
∠2=110o
∵两直线行,内错角相等
∠3=110o
∵两直线平行,同位角相等
∠4=70o
∵两直线平行,同旁内角互补
一、快速抢答
2、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
B
C
∠C=142o
∵两直线平行,内错角相等
一、快速抢答
3、如图直线 a ∥ b,直线b垂直于直线c,则直线a垂直于直线c吗
∟
∟
a
b
c
a⊥b
∵两直线平行, 同位角相等
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
判定
性质
平行线的性质和平行线的判定方法的 区 别 与 联 系
小结
