五年级下册数学教案-3.4 《长方体和正方体的体积计算》 西师大版
文档属性
| 名称 | 五年级下册数学教案-3.4 《长方体和正方体的体积计算》 西师大版 |  | |
| 格式 | doc | ||
| 文件大小 | 487.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 08:17:53 | ||
图片预览



文档简介
西师大版五年级下册第三单元
《长方体和正方体的体积计算》教学设计
课题 长方体和正方体的体积计算 单元 第三单元 学科 数学 年级 五年级
学习 目标 1.结合摆一摆,探索并掌握长方体、正方体体积的计算方法,并运用公式正确计算。
2.通过学生的自主探索与合作交流,培养学生的实际操作能力,同时发展他们的空间观念。
3.在合作交流中,激发学生学习数学、发现数学的兴趣,学会与人合作。
重点 探究并掌握长方体、正方体体积的计算方法。
难点 理解长方体和正方体体积公式的推导过程。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、复习旧知
1.填一填。
(1)物体所占空间的大小叫做物体的( )。
(2)常用的体积单位有:( )、( )、 ( )。
2.下列图形都是用体积为1立方厘米的小正方体拼成的,分别求出它们的体积。
引导学生总结出:有几个小正方体就是几立方厘米。
二、导入新课
师:刚才我们通过数一数的方式可以求出一个长方体或正方体的体积,是不是以后都要通过数一数的方式来求出长方体或正方体的体积呢?
师:那么关于长方体或正方体的体积你们有什么想知道的吗?
反馈:长方体或正方体的体积与什么有关?
长方体或正方体的体积怎样计算?
师:今天我们就来探讨这方面的知识,希望大家通过这节课的学习能够学有收获。
板书课题:长方体和正方体的体积计算
学生独自完成,然后集体订正。
学生:不是,应该有计算的方法。
学生自由说说。
通过复习,检查学生掌握知识的情况,为后面的学习奠定基础。
通过谈话,引起学生的认知冲突,为开课做准备。
讲授新课 探究长方体的体积计算方法
师:大家大胆猜猜,长方体的体积可能与谁有关系?
师:是这样吗?现在我们来摆一摆,看看大家能够找到想要的答案吗?
课件出示:
长方体动画演示
师:大家发现了什么?
反馈:
长方体的宽、高不变,长变短了,体积变小了;
长方体的长、高不变,宽变长了,体积变大了;
长方体的长、宽不变,高变长了,体积变大了。
师:找到大家要的答案了吗?
师:长方体的体积与长、宽、高有怎样的关系呢?大家想不想知道?
师:拿出你们课前准备的小正方体,我们一起去摆一摆好吗?
课件出示合作提示:
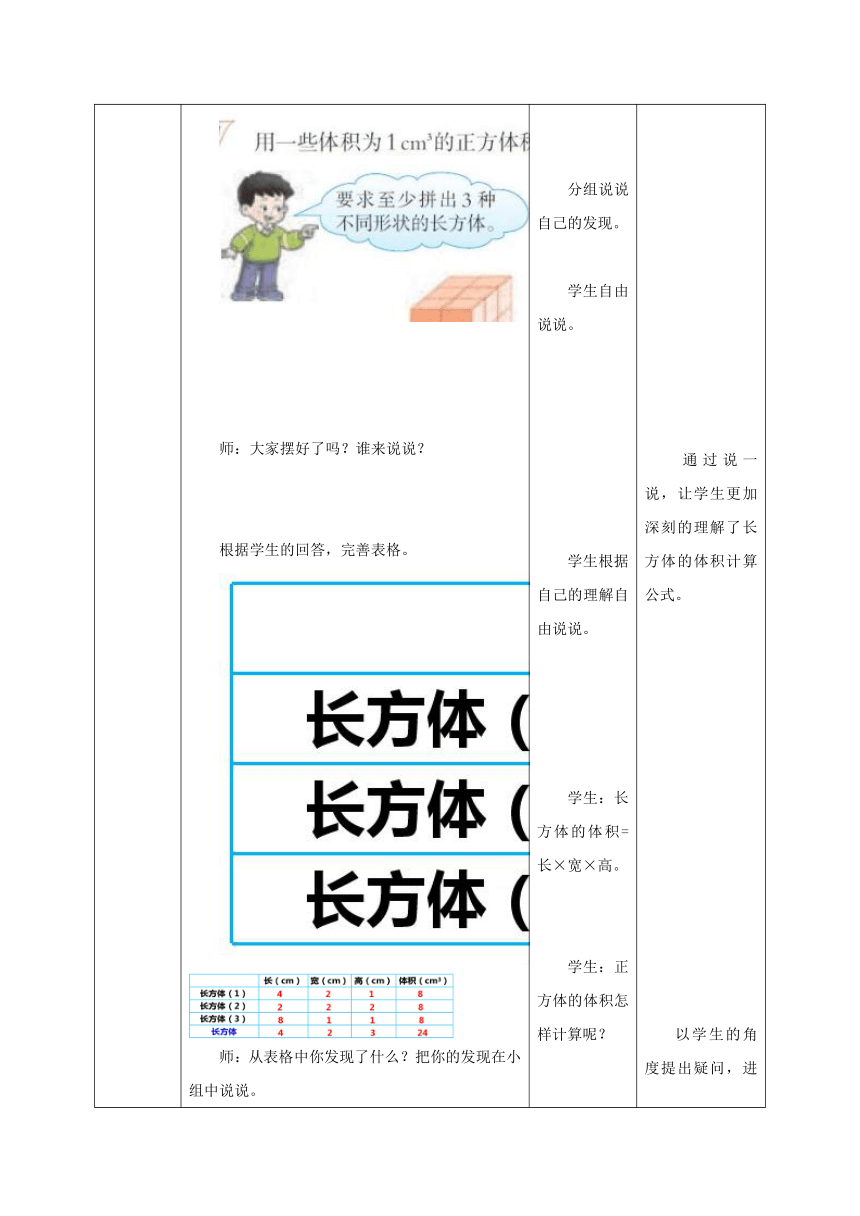
同桌合作,用一些体积为1cm3的正方体积木拼长方体。
要求至少摆出3种不同形状的长方体。
观察长方体模型并填写表格。
师:大家摆好了吗?谁来说说?
根据学生的回答,完善表格。
师:从表格中你发现了什么?把你的发现在小组中说说。
师:谁来说说你的发现?
反馈:长、宽、高的乘积等于长方体的体积;
还有不管有多少小正方体组成的长方体,体积都等于长、宽、高的乘积;
……
师:这么多的发现呀!可是老师有一个疑问:长方体的体积为什么等于长×宽×高呢?
反馈:长方体中包含有多少个1立方厘米的正方体,长方体的体积就是多少。
师:原来是这样呀!现在你能根据上面的数据归纳出长方体的体积计算方法了吗?
二、探索正方体体积的计算方法
师:关于体积你们还想知道什么呢?
师:有谁知道呢?
师:能说说你的想法吗?
反馈:正方体是长、宽、高相等的长方体,而长方体的体积是“长×宽×高”,所以正方体的体积=棱长×棱长×棱长。
三、统一公式
师:老师在大家学习长方体和正方体的体积计算方法时,发现了一个非常有趣的规律,你们想知道吗?
课件出示:
师:图中阴影部分的面积是上面各个图形底面的面积,你能说说长方体和正方体的底面积是怎么计算的?
反馈:
长方体的底面积=长×宽,正方体的底面积=棱长×棱长。
根据学生的回答,课件出示:
师:你发现了什么?
反馈:长方体(正方体)的体积=底面积×高。
四、实践应用
师:大家已经知道长方体和正方体的体积计算方法了,那么你们能计算出这个水果箱的体积是多少吗?
课件出示:
师:想想,可以怎样计算呢?
反馈:
可以直接用长×宽×高求解;
也可以先算出底面积,然后再乘以高。
师:都是不错的方法!那么大家就在练习本上算算吧!
反馈:
60×30×20
=1800×20
=36000(立方厘米)
答:这个水果箱的体积是36000立方厘米。
学生:长方体的体积与长、宽、高有关。
学生观察。
学生自由说说。
学生:长方体的体积却是与长、宽、高有关。
学生:想。
学生:好。
同桌合作,用正方体积木拼长方体,并填写表格。
学生自由说说。
分组说说自己的发现。
学生自由说说。
学生根据自己的理解自由说说。
学生:长方体的体积=长×宽×高。
学生:正方体的体积怎样计算呢?
学生:正方体的体积=棱长×棱长×棱长。
学生自由说说。
学生:想。
学生自由说说。
学生分组说说。
学生自由说说。
学生独自计算,然后反馈交流。
先让学生同通过猜一猜,感受长方体的体积与什么有关,然后通过进一步验证得出结论,为后面的活动做准备。
本环节完全交给学生自主探究,可以让学生感受知识的产生、形成过程,为后面说说自己的发现做好准备,培养了学生观察、分析、比较、归纳、总结的思维能力。
通过说一说,让学生更加深刻的理解了长方体的体积计算公式。
以学生的角度提出疑问,进而引出探究正方体体积计算方法,极大的提高了学生探究新知的欲望。
这部分交给学生自己探索,充分让学生明确知识之间的相互联系,进而增强学习数学的信心与兴趣。
利用实践应用,不仅可以巩固学生掌握的知识,同时体现了学习知识的价值。
巩固练习 1.说一说,你的教室的空间有多大?
师:要求教室的空间有多大,需要怎么做?
反馈:要测量教室的长、宽、高;
我估计教室的长是9米,宽是7米;
教室的高大约是3.5米。
师:赶紧利用估计的数据算算看。
2.一个长方体木箱,长是6分米,宽是5分米,高是3分米,这个木箱的容积是多少升?
3.(1)一个长方体的体积是56立方米,底面积是8平方米,高是多少米?
(2)一个长方体的体积是56立方米,高是4米,底面积是多少平方米?
4.将一个长20cm,宽6cm,高5cm的长方体截成一个体积最大的正方体,这个正方体的体积是多少?
5.拓展提高
有甲、乙两个水箱(如下图),在甲箱中加入水,水深为15cm,如果把这些水倒人乙箱,水深多少厘米?(单位:cm)
30×5×15÷15÷20=7.5(cm)
6.布置作业
教材练习十五第1~3题。
学生自由说说。
学生独自完成,然后集体订正。
通过不同类型的练习,充分训练了学生解决问题的能力,同时提高学生的思维能力与探究的敏捷性。
课堂小结 通过本节课的学习,你们有什么收获?
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体(正方体)的体积=底面积×高
学生自由说一说。 通过总结帮助学生回忆今天学习的新知,梳理知识之间的联系。
板书 长方体和正方体的体积计算
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
通过简洁、有效的板书,帮助学生形成知识体系。
《长方体和正方体的体积计算》教学设计
课题 长方体和正方体的体积计算 单元 第三单元 学科 数学 年级 五年级
学习 目标 1.结合摆一摆,探索并掌握长方体、正方体体积的计算方法,并运用公式正确计算。
2.通过学生的自主探索与合作交流,培养学生的实际操作能力,同时发展他们的空间观念。
3.在合作交流中,激发学生学习数学、发现数学的兴趣,学会与人合作。
重点 探究并掌握长方体、正方体体积的计算方法。
难点 理解长方体和正方体体积公式的推导过程。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、复习旧知
1.填一填。
(1)物体所占空间的大小叫做物体的( )。
(2)常用的体积单位有:( )、( )、 ( )。
2.下列图形都是用体积为1立方厘米的小正方体拼成的,分别求出它们的体积。
引导学生总结出:有几个小正方体就是几立方厘米。
二、导入新课
师:刚才我们通过数一数的方式可以求出一个长方体或正方体的体积,是不是以后都要通过数一数的方式来求出长方体或正方体的体积呢?
师:那么关于长方体或正方体的体积你们有什么想知道的吗?
反馈:长方体或正方体的体积与什么有关?
长方体或正方体的体积怎样计算?
师:今天我们就来探讨这方面的知识,希望大家通过这节课的学习能够学有收获。
板书课题:长方体和正方体的体积计算
学生独自完成,然后集体订正。
学生:不是,应该有计算的方法。
学生自由说说。
通过复习,检查学生掌握知识的情况,为后面的学习奠定基础。
通过谈话,引起学生的认知冲突,为开课做准备。
讲授新课 探究长方体的体积计算方法
师:大家大胆猜猜,长方体的体积可能与谁有关系?
师:是这样吗?现在我们来摆一摆,看看大家能够找到想要的答案吗?
课件出示:
长方体动画演示
师:大家发现了什么?
反馈:
长方体的宽、高不变,长变短了,体积变小了;
长方体的长、高不变,宽变长了,体积变大了;
长方体的长、宽不变,高变长了,体积变大了。
师:找到大家要的答案了吗?
师:长方体的体积与长、宽、高有怎样的关系呢?大家想不想知道?
师:拿出你们课前准备的小正方体,我们一起去摆一摆好吗?
课件出示合作提示:
同桌合作,用一些体积为1cm3的正方体积木拼长方体。
要求至少摆出3种不同形状的长方体。
观察长方体模型并填写表格。
师:大家摆好了吗?谁来说说?
根据学生的回答,完善表格。
师:从表格中你发现了什么?把你的发现在小组中说说。
师:谁来说说你的发现?
反馈:长、宽、高的乘积等于长方体的体积;
还有不管有多少小正方体组成的长方体,体积都等于长、宽、高的乘积;
……
师:这么多的发现呀!可是老师有一个疑问:长方体的体积为什么等于长×宽×高呢?
反馈:长方体中包含有多少个1立方厘米的正方体,长方体的体积就是多少。
师:原来是这样呀!现在你能根据上面的数据归纳出长方体的体积计算方法了吗?
二、探索正方体体积的计算方法
师:关于体积你们还想知道什么呢?
师:有谁知道呢?
师:能说说你的想法吗?
反馈:正方体是长、宽、高相等的长方体,而长方体的体积是“长×宽×高”,所以正方体的体积=棱长×棱长×棱长。
三、统一公式
师:老师在大家学习长方体和正方体的体积计算方法时,发现了一个非常有趣的规律,你们想知道吗?
课件出示:
师:图中阴影部分的面积是上面各个图形底面的面积,你能说说长方体和正方体的底面积是怎么计算的?
反馈:
长方体的底面积=长×宽,正方体的底面积=棱长×棱长。
根据学生的回答,课件出示:
师:你发现了什么?
反馈:长方体(正方体)的体积=底面积×高。
四、实践应用
师:大家已经知道长方体和正方体的体积计算方法了,那么你们能计算出这个水果箱的体积是多少吗?
课件出示:
师:想想,可以怎样计算呢?
反馈:
可以直接用长×宽×高求解;
也可以先算出底面积,然后再乘以高。
师:都是不错的方法!那么大家就在练习本上算算吧!
反馈:
60×30×20
=1800×20
=36000(立方厘米)
答:这个水果箱的体积是36000立方厘米。
学生:长方体的体积与长、宽、高有关。
学生观察。
学生自由说说。
学生:长方体的体积却是与长、宽、高有关。
学生:想。
学生:好。
同桌合作,用正方体积木拼长方体,并填写表格。
学生自由说说。
分组说说自己的发现。
学生自由说说。
学生根据自己的理解自由说说。
学生:长方体的体积=长×宽×高。
学生:正方体的体积怎样计算呢?
学生:正方体的体积=棱长×棱长×棱长。
学生自由说说。
学生:想。
学生自由说说。
学生分组说说。
学生自由说说。
学生独自计算,然后反馈交流。
先让学生同通过猜一猜,感受长方体的体积与什么有关,然后通过进一步验证得出结论,为后面的活动做准备。
本环节完全交给学生自主探究,可以让学生感受知识的产生、形成过程,为后面说说自己的发现做好准备,培养了学生观察、分析、比较、归纳、总结的思维能力。
通过说一说,让学生更加深刻的理解了长方体的体积计算公式。
以学生的角度提出疑问,进而引出探究正方体体积计算方法,极大的提高了学生探究新知的欲望。
这部分交给学生自己探索,充分让学生明确知识之间的相互联系,进而增强学习数学的信心与兴趣。
利用实践应用,不仅可以巩固学生掌握的知识,同时体现了学习知识的价值。
巩固练习 1.说一说,你的教室的空间有多大?
师:要求教室的空间有多大,需要怎么做?
反馈:要测量教室的长、宽、高;
我估计教室的长是9米,宽是7米;
教室的高大约是3.5米。
师:赶紧利用估计的数据算算看。
2.一个长方体木箱,长是6分米,宽是5分米,高是3分米,这个木箱的容积是多少升?
3.(1)一个长方体的体积是56立方米,底面积是8平方米,高是多少米?
(2)一个长方体的体积是56立方米,高是4米,底面积是多少平方米?
4.将一个长20cm,宽6cm,高5cm的长方体截成一个体积最大的正方体,这个正方体的体积是多少?
5.拓展提高
有甲、乙两个水箱(如下图),在甲箱中加入水,水深为15cm,如果把这些水倒人乙箱,水深多少厘米?(单位:cm)
30×5×15÷15÷20=7.5(cm)
6.布置作业
教材练习十五第1~3题。
学生自由说说。
学生独自完成,然后集体订正。
通过不同类型的练习,充分训练了学生解决问题的能力,同时提高学生的思维能力与探究的敏捷性。
课堂小结 通过本节课的学习,你们有什么收获?
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体(正方体)的体积=底面积×高
学生自由说一说。 通过总结帮助学生回忆今天学习的新知,梳理知识之间的联系。
板书 长方体和正方体的体积计算
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
通过简洁、有效的板书,帮助学生形成知识体系。
