1.7整式的除法-2020-2021学年北师大版七年级数学下册同步提升训练试卷(Word版含答案)
文档属性
| 名称 | 1.7整式的除法-2020-2021学年北师大版七年级数学下册同步提升训练试卷(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 111.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 09:26:05 | ||
图片预览



文档简介
2021年度北师大版七年级数学下册《1.7整式的除法》同步提升训练(附答案)
1.下列运算正确的是( )
A.3a2+2a=5a2
B.﹣8a7÷4a=2a6
C.(﹣2a2)3=﹣8a6
D.4a3?3a2=12a6
2.计算(﹣2m2)3÷(m?m)2的结果是( )
A.﹣2m
B.2m2
C.﹣8m2
D.﹣8m
3.一个长方形的面积为4x2﹣8xy,且一边长为2x,则另一边的长为( )
A.2x﹣4y
B.2x﹣4xy
C.2x2﹣4xy
D.2x2﹣4y
4.如果“□×2ab=4a2b”,那么“□”内应填的代数式是( )
A.2b
B.2ab
C.a
D.2a
5.计算﹣6a3b2÷2a2b的结果是( )
A.﹣3ab2
B.﹣3ab
C.3ab
D.3ab2
6.下列计算正确的个数是( )
①x2x3=x5②x2+x2=2x4③(﹣2x)2=﹣4x2④(﹣2x2)(﹣3x)3=6x5
⑤x3y3÷(xy)2=xy⑥(﹣x2)3=﹣x6
A.2个
B.3个
C.4个
D.5个
7.计算:(12x3﹣8x2+16x)÷(﹣4x)的结果是( )
A.﹣3x2+2x﹣4
B.﹣3x2﹣2x+4
C.﹣3x2+2x+4
D.3x2﹣2x+4
8.小亮在计算(6x3y﹣3x2y2)÷3xy时,错把括号内的减号写成了加号,那么正确结果与错误结果的乘积是( )
A.2x2﹣xy
B.2x2+xy
C.4x4﹣x2y2
D.无法计算
9.计算:(21a5﹣7a2)÷(7a)=
.
10.已知a+b=0,则代数式a(a+4b)﹣(a+2b)(a﹣2b)的值为
.
11.如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是
.
12.计算:(﹣2a﹣2b)3÷2a﹣8b﹣3=
.
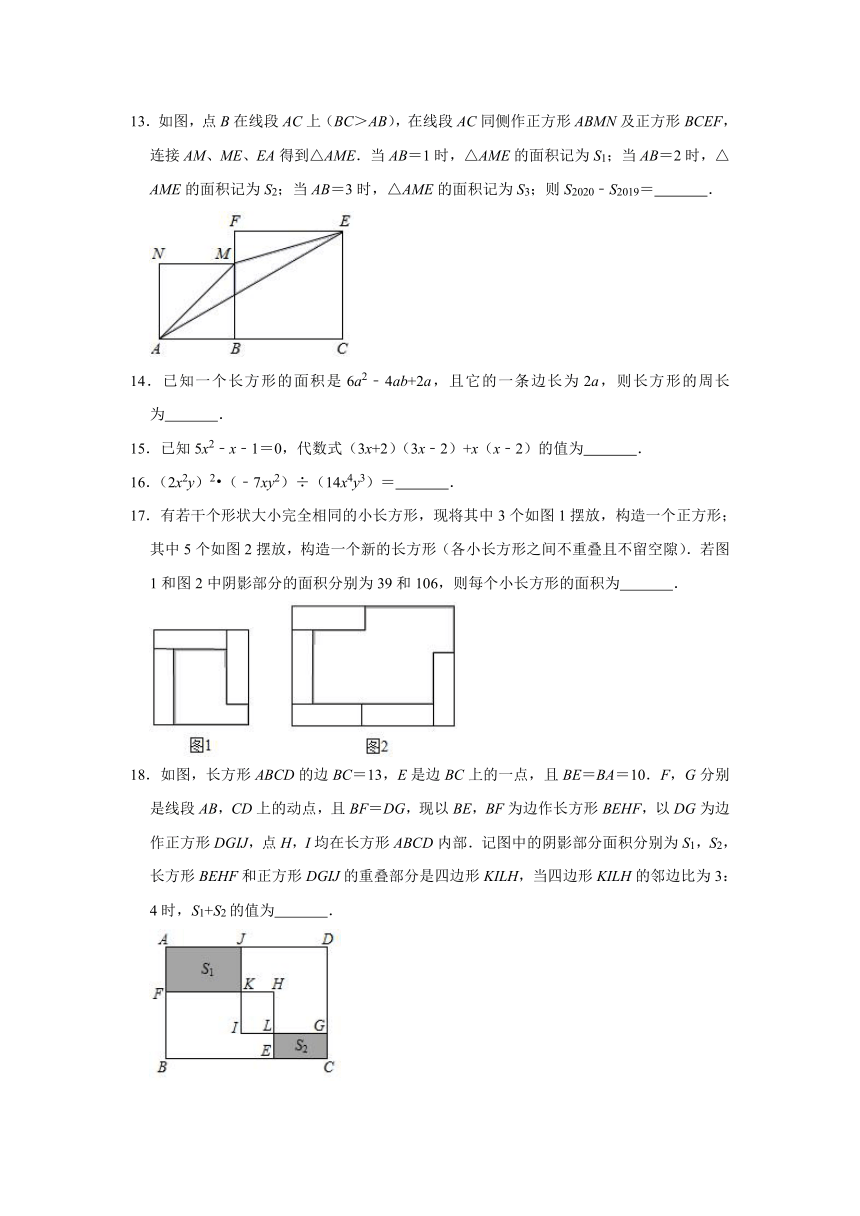
13.如图,点B在线段AC上(BC>AB),在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;则S2020﹣S2019=
.
14.已知一个长方形的面积是6a2﹣4ab+2a,且它的一条边长为2a,则长方形的周长为
.
15.已知5x2﹣x﹣1=0,代数式(3x+2)(3x﹣2)+x(x﹣2)的值为
.
16.(2x2y)2?(﹣7xy2)÷(14x4y3)=
.
17.有若干个形状大小完全相同的小长方形,现将其中3个如图1摆放,构造一个正方形;其中5个如图2摆放,构造一个新的长方形(各小长方形之间不重叠且不留空隙).若图1和图2中阴影部分的面积分别为39和106,则每个小长方形的面积为
.
18.如图,长方形ABCD的边BC=13,E是边BC上的一点,且BE=BA=10.F,G分别是线段AB,CD上的动点,且BF=DG,现以BE,BF为边作长方形BEHF,以DG为边作正方形DGIJ,点H,I均在长方形ABCD内部.记图中的阴影部分面积分别为S1,S2,长方形BEHF和正方形DGIJ的重叠部分是四边形KILH,当四边形KILH的邻边比为3:4时,S1+S2的值为
.
19.若2m×8n=32,,则的值为
.
20.如果x2+3x=2020,那么代数式x(2x+1)﹣(x﹣1)2的值为
.
21.化简:2x(x﹣3y)+(5xy2﹣2x2y)÷y.
22.先化简,再求值:(3a5b3+a4b2)÷(﹣a2b)2﹣(2+a)(2﹣a)﹣(a﹣b)2,其中a=﹣,b=2.
23.计算:
(1);
(2)(﹣2×1012)×(﹣2×102)3÷(0.5×103)3;
(3);
(4)(a﹣2b+3c)×(a+2b﹣3c);
(5)(﹣2m﹣3)2(3﹣2m)2;
(6)4×1.632+6.52×6.74+6.742.(用乘法公式计算)
24.已知:|a﹣b﹣1|+a2﹣4a+4=0,化简求值:[(3a﹣2b)2﹣(a﹣3b)(2a+b)+(3a+b)(3a﹣b)﹣6b2]÷(﹣a).
25.先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
26.先化简,再求值:[b(a﹣b)﹣a(3a﹣2b)+(3a﹣b)(﹣b﹣3a)]÷(﹣3a),其中(a﹣)2+|b﹣|=0.
参考答案
1.解:A、3a2与2a不是同类项,不能合并,故A选项错误.
B、原式=﹣2a6,故B选项错误.
C、原式=﹣8a6,故C选项正确.
D、原式=12a5,故D选项错误.
故选:C.
2.解:原式=﹣8m6÷m4=﹣8m2.
故选:C.
3.解:∵一个长方形的面积为4x2﹣8xy,且一边长为2x,
∴另一边的长为:(4x2﹣8xy)÷2x=2x﹣4y.
故选:A.
4.解:□×2ab=4a2b,
∴4a2b÷2ab=2a,
则“□”内应填的代数式是2a.
故选:D.
5.解:﹣6a3b2÷2a2b=﹣3ab,
故选:B.
6.解:x2?x3=x5,故①正确;
x2+x2=2x2,故②错误;
(﹣2x)2=4x2,故③错误;
(﹣2x2)?(﹣3x)3=(﹣2x2)?(﹣27x3)=54x5,故④错误;
x3y3÷(xy)2=x3y3÷(x2y2)=xy,故⑤正确;
(﹣x2)3=﹣x6,故⑥正确;
故选:B.
7.解:(12x3﹣8x2+16x)÷(﹣4x)=﹣3x2+2x﹣4;
故选:A.
8.解:正确结果为:
原式=6x3y÷3xy﹣3x2y2÷3xy=2x2﹣xy,
错误结果为:
原式=6x3y÷3xy+3x2y2÷3xy
=2x2+xy,
∴(2x2﹣xy)(2x2+xy)=4x4﹣x2y2,
故选:C.
9.解:原式=21a5÷7a﹣7a2÷7a=3a4﹣a.
故答案为:3a4﹣a.
10.解:原式=a2+4ab﹣(a2﹣4b2)=a2+4ab﹣a2+4b2=4ab+4b2=4b(a+b),
当a+b=0时,
原式=0.
故答案为:0.
11.解:设大正方形的边长为a,小正方形的边长为b,
故阴影部分的面积是:AE?BC+AE?BD=AE(BC+BD)
=(AB﹣BE)(BC+BD)=(a﹣b)(a+b)=(a2﹣b2)=×60=30.
故答案为:30.
12.解:(﹣2a﹣2b)3÷2a﹣8b﹣3=﹣8a﹣6b3÷2a﹣8b﹣3=﹣4a2b6.
故答案为:﹣4a2b6.
13.解:如图,连接BE,
∵在线段AC同侧作正方形ABMN及正方形BCEF,
∴BC∥AM,
∴△AME与△AMB同底等高,
∴S△AME=S△AMB,
∴当AB=n时,△AME的面积记为Sn=;
Sn﹣1==﹣n+,
∴当n≥2时,Sn﹣Sn﹣1=﹣(﹣n+)=n﹣=,
∴S2020﹣S2019==.
故答案为:.
14.解:∵一个长方形的面积是6a2﹣4ab+2a,且它的一条边长为2a,
∴长方形的另一边长为:(6a2﹣4ab+2a)÷2a=3a﹣2b+1,
故长方形的周长为:2(3a﹣2b+1+2a)=10a﹣4b+2.
故答案为:10a﹣4b+2.
15.解:∵5x2﹣x﹣1=0,
∴5x2﹣x=1,
原式=9x2﹣4+x2﹣2x=10x2﹣2x﹣4=2(5x2﹣x)﹣4=2×1﹣4=2﹣4=﹣2,
故答案为:﹣2.
16.解:原式=(4x4y2)?(﹣7xy2)÷(14x4y3)=﹣28x5y4÷(14x4y3)=﹣2xy.
故答案为:﹣2xy.
17.解:设小长方形的宽为a,长为b,根据题意可得:
(a+b)2﹣3ab=39,
故a2+b2﹣ab=39,
(2b+a)(2a+b)﹣5ab=106,
故4ab+2b2+2a2+ab﹣5ab=106,
则2a2+2b2=106,
即a2+b2=53,
则53﹣ab=39,
解得:ab=14,
故每个小长方形的面积为:14.
故答案为:14.
18.解:在矩形ABCD中,AB=CD=10,AD=BC=13.
∵四边形DGIJ为正方形,四边形BFHE为矩形,BF=DG,
∴四边形KILH为矩形,KI=HL=2DG﹣AB=2DG﹣10.
∵BE=BA=10,
∴LG=EC=3,
∴KH=IL=DG﹣LG=DG﹣3.
当矩形KILH的邻边的比为3:4时,(DG﹣3):(2DG﹣10)=3:4,或(2DG﹣10):(DG﹣3)=3:4,
解得DG=9或.
当DG=9时,AF=CG=1,AJ=4,
∴S1+S2=AF?AJ+CE?CG=1×4+1×3=7;
当DG=时,AF=CG=,AJ=,
∴S1+S2=AF?AJ+CE?CG==.
故答案为7或.
19.解:∵2m×8n=2m×23n=2m+3n=32=25,2m÷4n=2m÷22n=2m﹣2n==2﹣4,
∴m+3n=5,m﹣2n=﹣4,
两式相加得:2m+n=1,
则原式=(2m+n)=.
故答案为:.
20.解:x(2x+1)﹣(x﹣1)2=2x2+x﹣x2+2x﹣1=x2+3x﹣1,
∵x2+3x=2020,
∴原式=2020﹣1=2019,
故答案为:2019.
21.解:原式=2x2﹣6xy+5xy﹣2x2=﹣xy.
22.解:原式=:(3a5b3+a4b2)÷a4b2﹣(4﹣a2)﹣(a2﹣2ab+b2)
=3ab+1﹣4+a2﹣a2+2ab﹣b2=5ab﹣b2﹣3,
当,b=2时,
原式==﹣9.
23.解:(1)=2+1﹣9+(﹣1)=﹣7;
(2)(﹣2×1012)×(﹣2×102)3÷(0.5×103)3
=(﹣2×1012)×(﹣23×106)÷(×109)=27×109=128×109=1.28×1011;
(3)=﹣x3y3+3x2y3;
(4)(a﹣2b+3c)×(a+2b﹣3c)=[a﹣(2b﹣3c)][a+(2b﹣3c)]
=a2﹣(2b﹣3c)2=a2﹣4b2+12bc﹣9c2;
(5)(﹣2m﹣3)2(3﹣2m)2=(2m+3)2?(3﹣2m)2=[(3+2m)(3﹣2m)]2
=(9﹣4m2)2=81﹣72m2+16m4;
(6)4×1.632+6.52×6.74+6.742
=(2×1.63)2+2×3.26×6.74+6.742
=3.262+2×3.26×6.74+6.742=(3.26+6.74)2=102=100.
24.解:∵|a﹣b﹣1|+a2﹣4a+4=0,
∴|a﹣b﹣1|+(a﹣2)2=0,
∴a=2,b=1,
∴[(3a﹣2b)2﹣(a﹣3b)(2a+b)+(3a+b)(3a﹣b)﹣6b2]÷(﹣a)
=[9a2﹣12ab+4b2﹣(2a2+ab﹣6ab﹣3b2)+9a2﹣b2﹣6b2]÷(﹣a)
=(16a2﹣7ab)÷(﹣a)=﹣48a+21b,
将a=2,b=1,代入上式可得:
原式=﹣48×2+21×1=﹣75.
25.解:(1)6x2y(﹣2xy+y3)÷xy2,
=(﹣12x3y2+6x2y4)÷xy2
=﹣12x2+6xy2,
当x=2,y=﹣1时,
原式=﹣12×22+6×2×(﹣1)2=﹣36;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y)
=x2﹣4y2+x2﹣4xy+4y2﹣3x2+xy=﹣x2﹣3xy,
当x=﹣2,y=时,
原式=﹣(﹣2)2﹣3×(﹣2)×=﹣4+3=﹣1.
26.解:原式=(ab﹣b2﹣3a2+2ab+b2﹣9a2)÷(﹣3a)
=(3ab﹣12a2)÷(﹣3a)=﹣b+4a,
∵(a﹣)2+|b﹣|=0,
∴a﹣=0,b﹣=0,
解得:a=,b=,
当a=,b=时,
原式=﹣+4×=﹣+2=.
1.下列运算正确的是( )
A.3a2+2a=5a2
B.﹣8a7÷4a=2a6
C.(﹣2a2)3=﹣8a6
D.4a3?3a2=12a6
2.计算(﹣2m2)3÷(m?m)2的结果是( )
A.﹣2m
B.2m2
C.﹣8m2
D.﹣8m
3.一个长方形的面积为4x2﹣8xy,且一边长为2x,则另一边的长为( )
A.2x﹣4y
B.2x﹣4xy
C.2x2﹣4xy
D.2x2﹣4y
4.如果“□×2ab=4a2b”,那么“□”内应填的代数式是( )
A.2b
B.2ab
C.a
D.2a
5.计算﹣6a3b2÷2a2b的结果是( )
A.﹣3ab2
B.﹣3ab
C.3ab
D.3ab2
6.下列计算正确的个数是( )
①x2x3=x5②x2+x2=2x4③(﹣2x)2=﹣4x2④(﹣2x2)(﹣3x)3=6x5
⑤x3y3÷(xy)2=xy⑥(﹣x2)3=﹣x6
A.2个
B.3个
C.4个
D.5个
7.计算:(12x3﹣8x2+16x)÷(﹣4x)的结果是( )
A.﹣3x2+2x﹣4
B.﹣3x2﹣2x+4
C.﹣3x2+2x+4
D.3x2﹣2x+4
8.小亮在计算(6x3y﹣3x2y2)÷3xy时,错把括号内的减号写成了加号,那么正确结果与错误结果的乘积是( )
A.2x2﹣xy
B.2x2+xy
C.4x4﹣x2y2
D.无法计算
9.计算:(21a5﹣7a2)÷(7a)=
.
10.已知a+b=0,则代数式a(a+4b)﹣(a+2b)(a﹣2b)的值为
.
11.如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是
.
12.计算:(﹣2a﹣2b)3÷2a﹣8b﹣3=
.
13.如图,点B在线段AC上(BC>AB),在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;则S2020﹣S2019=
.
14.已知一个长方形的面积是6a2﹣4ab+2a,且它的一条边长为2a,则长方形的周长为
.
15.已知5x2﹣x﹣1=0,代数式(3x+2)(3x﹣2)+x(x﹣2)的值为
.
16.(2x2y)2?(﹣7xy2)÷(14x4y3)=
.
17.有若干个形状大小完全相同的小长方形,现将其中3个如图1摆放,构造一个正方形;其中5个如图2摆放,构造一个新的长方形(各小长方形之间不重叠且不留空隙).若图1和图2中阴影部分的面积分别为39和106,则每个小长方形的面积为
.
18.如图,长方形ABCD的边BC=13,E是边BC上的一点,且BE=BA=10.F,G分别是线段AB,CD上的动点,且BF=DG,现以BE,BF为边作长方形BEHF,以DG为边作正方形DGIJ,点H,I均在长方形ABCD内部.记图中的阴影部分面积分别为S1,S2,长方形BEHF和正方形DGIJ的重叠部分是四边形KILH,当四边形KILH的邻边比为3:4时,S1+S2的值为
.
19.若2m×8n=32,,则的值为
.
20.如果x2+3x=2020,那么代数式x(2x+1)﹣(x﹣1)2的值为
.
21.化简:2x(x﹣3y)+(5xy2﹣2x2y)÷y.
22.先化简,再求值:(3a5b3+a4b2)÷(﹣a2b)2﹣(2+a)(2﹣a)﹣(a﹣b)2,其中a=﹣,b=2.
23.计算:
(1);
(2)(﹣2×1012)×(﹣2×102)3÷(0.5×103)3;
(3);
(4)(a﹣2b+3c)×(a+2b﹣3c);
(5)(﹣2m﹣3)2(3﹣2m)2;
(6)4×1.632+6.52×6.74+6.742.(用乘法公式计算)
24.已知:|a﹣b﹣1|+a2﹣4a+4=0,化简求值:[(3a﹣2b)2﹣(a﹣3b)(2a+b)+(3a+b)(3a﹣b)﹣6b2]÷(﹣a).
25.先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
26.先化简,再求值:[b(a﹣b)﹣a(3a﹣2b)+(3a﹣b)(﹣b﹣3a)]÷(﹣3a),其中(a﹣)2+|b﹣|=0.
参考答案
1.解:A、3a2与2a不是同类项,不能合并,故A选项错误.
B、原式=﹣2a6,故B选项错误.
C、原式=﹣8a6,故C选项正确.
D、原式=12a5,故D选项错误.
故选:C.
2.解:原式=﹣8m6÷m4=﹣8m2.
故选:C.
3.解:∵一个长方形的面积为4x2﹣8xy,且一边长为2x,
∴另一边的长为:(4x2﹣8xy)÷2x=2x﹣4y.
故选:A.
4.解:□×2ab=4a2b,
∴4a2b÷2ab=2a,
则“□”内应填的代数式是2a.
故选:D.
5.解:﹣6a3b2÷2a2b=﹣3ab,
故选:B.
6.解:x2?x3=x5,故①正确;
x2+x2=2x2,故②错误;
(﹣2x)2=4x2,故③错误;
(﹣2x2)?(﹣3x)3=(﹣2x2)?(﹣27x3)=54x5,故④错误;
x3y3÷(xy)2=x3y3÷(x2y2)=xy,故⑤正确;
(﹣x2)3=﹣x6,故⑥正确;
故选:B.
7.解:(12x3﹣8x2+16x)÷(﹣4x)=﹣3x2+2x﹣4;
故选:A.
8.解:正确结果为:
原式=6x3y÷3xy﹣3x2y2÷3xy=2x2﹣xy,
错误结果为:
原式=6x3y÷3xy+3x2y2÷3xy
=2x2+xy,
∴(2x2﹣xy)(2x2+xy)=4x4﹣x2y2,
故选:C.
9.解:原式=21a5÷7a﹣7a2÷7a=3a4﹣a.
故答案为:3a4﹣a.
10.解:原式=a2+4ab﹣(a2﹣4b2)=a2+4ab﹣a2+4b2=4ab+4b2=4b(a+b),
当a+b=0时,
原式=0.
故答案为:0.
11.解:设大正方形的边长为a,小正方形的边长为b,
故阴影部分的面积是:AE?BC+AE?BD=AE(BC+BD)
=(AB﹣BE)(BC+BD)=(a﹣b)(a+b)=(a2﹣b2)=×60=30.
故答案为:30.
12.解:(﹣2a﹣2b)3÷2a﹣8b﹣3=﹣8a﹣6b3÷2a﹣8b﹣3=﹣4a2b6.
故答案为:﹣4a2b6.
13.解:如图,连接BE,
∵在线段AC同侧作正方形ABMN及正方形BCEF,
∴BC∥AM,
∴△AME与△AMB同底等高,
∴S△AME=S△AMB,
∴当AB=n时,△AME的面积记为Sn=;
Sn﹣1==﹣n+,
∴当n≥2时,Sn﹣Sn﹣1=﹣(﹣n+)=n﹣=,
∴S2020﹣S2019==.
故答案为:.
14.解:∵一个长方形的面积是6a2﹣4ab+2a,且它的一条边长为2a,
∴长方形的另一边长为:(6a2﹣4ab+2a)÷2a=3a﹣2b+1,
故长方形的周长为:2(3a﹣2b+1+2a)=10a﹣4b+2.
故答案为:10a﹣4b+2.
15.解:∵5x2﹣x﹣1=0,
∴5x2﹣x=1,
原式=9x2﹣4+x2﹣2x=10x2﹣2x﹣4=2(5x2﹣x)﹣4=2×1﹣4=2﹣4=﹣2,
故答案为:﹣2.
16.解:原式=(4x4y2)?(﹣7xy2)÷(14x4y3)=﹣28x5y4÷(14x4y3)=﹣2xy.
故答案为:﹣2xy.
17.解:设小长方形的宽为a,长为b,根据题意可得:
(a+b)2﹣3ab=39,
故a2+b2﹣ab=39,
(2b+a)(2a+b)﹣5ab=106,
故4ab+2b2+2a2+ab﹣5ab=106,
则2a2+2b2=106,
即a2+b2=53,
则53﹣ab=39,
解得:ab=14,
故每个小长方形的面积为:14.
故答案为:14.
18.解:在矩形ABCD中,AB=CD=10,AD=BC=13.
∵四边形DGIJ为正方形,四边形BFHE为矩形,BF=DG,
∴四边形KILH为矩形,KI=HL=2DG﹣AB=2DG﹣10.
∵BE=BA=10,
∴LG=EC=3,
∴KH=IL=DG﹣LG=DG﹣3.
当矩形KILH的邻边的比为3:4时,(DG﹣3):(2DG﹣10)=3:4,或(2DG﹣10):(DG﹣3)=3:4,
解得DG=9或.
当DG=9时,AF=CG=1,AJ=4,
∴S1+S2=AF?AJ+CE?CG=1×4+1×3=7;
当DG=时,AF=CG=,AJ=,
∴S1+S2=AF?AJ+CE?CG==.
故答案为7或.
19.解:∵2m×8n=2m×23n=2m+3n=32=25,2m÷4n=2m÷22n=2m﹣2n==2﹣4,
∴m+3n=5,m﹣2n=﹣4,
两式相加得:2m+n=1,
则原式=(2m+n)=.
故答案为:.
20.解:x(2x+1)﹣(x﹣1)2=2x2+x﹣x2+2x﹣1=x2+3x﹣1,
∵x2+3x=2020,
∴原式=2020﹣1=2019,
故答案为:2019.
21.解:原式=2x2﹣6xy+5xy﹣2x2=﹣xy.
22.解:原式=:(3a5b3+a4b2)÷a4b2﹣(4﹣a2)﹣(a2﹣2ab+b2)
=3ab+1﹣4+a2﹣a2+2ab﹣b2=5ab﹣b2﹣3,
当,b=2时,
原式==﹣9.
23.解:(1)=2+1﹣9+(﹣1)=﹣7;
(2)(﹣2×1012)×(﹣2×102)3÷(0.5×103)3
=(﹣2×1012)×(﹣23×106)÷(×109)=27×109=128×109=1.28×1011;
(3)=﹣x3y3+3x2y3;
(4)(a﹣2b+3c)×(a+2b﹣3c)=[a﹣(2b﹣3c)][a+(2b﹣3c)]
=a2﹣(2b﹣3c)2=a2﹣4b2+12bc﹣9c2;
(5)(﹣2m﹣3)2(3﹣2m)2=(2m+3)2?(3﹣2m)2=[(3+2m)(3﹣2m)]2
=(9﹣4m2)2=81﹣72m2+16m4;
(6)4×1.632+6.52×6.74+6.742
=(2×1.63)2+2×3.26×6.74+6.742
=3.262+2×3.26×6.74+6.742=(3.26+6.74)2=102=100.
24.解:∵|a﹣b﹣1|+a2﹣4a+4=0,
∴|a﹣b﹣1|+(a﹣2)2=0,
∴a=2,b=1,
∴[(3a﹣2b)2﹣(a﹣3b)(2a+b)+(3a+b)(3a﹣b)﹣6b2]÷(﹣a)
=[9a2﹣12ab+4b2﹣(2a2+ab﹣6ab﹣3b2)+9a2﹣b2﹣6b2]÷(﹣a)
=(16a2﹣7ab)÷(﹣a)=﹣48a+21b,
将a=2,b=1,代入上式可得:
原式=﹣48×2+21×1=﹣75.
25.解:(1)6x2y(﹣2xy+y3)÷xy2,
=(﹣12x3y2+6x2y4)÷xy2
=﹣12x2+6xy2,
当x=2,y=﹣1时,
原式=﹣12×22+6×2×(﹣1)2=﹣36;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y)
=x2﹣4y2+x2﹣4xy+4y2﹣3x2+xy=﹣x2﹣3xy,
当x=﹣2,y=时,
原式=﹣(﹣2)2﹣3×(﹣2)×=﹣4+3=﹣1.
26.解:原式=(ab﹣b2﹣3a2+2ab+b2﹣9a2)÷(﹣3a)
=(3ab﹣12a2)÷(﹣3a)=﹣b+4a,
∵(a﹣)2+|b﹣|=0,
∴a﹣=0,b﹣=0,
解得:a=,b=,
当a=,b=时,
原式=﹣+4×=﹣+2=.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
