2.3平行线的性质-2020-2021学年北师大版七年级数学下册同步提升训练试卷(Word版含答案)
文档属性
| 名称 | 2.3平行线的性质-2020-2021学年北师大版七年级数学下册同步提升训练试卷(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 194.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 09:33:03 | ||
图片预览


文档简介
2021年度北师大版七年级数学下册《2.3平行线的性质》同步提升训练(附答案)
1.如图是郝老师的某次行车路线,总共拐了三次弯,最后行车路线与开始的路线是平行的,已知第一次转过的角度120°,第三次转过的角度135°,则第二次拐弯的角度是( )
A.75°
B.120°
C.135°
D.无法确定
2.如果∠α与∠β的两边分别平行,∠α比∠β的3倍少40°,则∠α的度数为( )
A.20°
B.125°
C.20°或125°
D.35°或110
3.如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )
A.∠A=∠C+∠E+∠F
B.∠A+∠E﹣∠C﹣∠F=180°
C.∠A﹣∠E+∠C+∠F=90°
D.∠A+∠E+∠C+∠F=360°
4.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A.30°
B.40°
C.50°
D.60°
5.如图,已知AD∥EF∥BC,BD∥GF,且BD平分∠ADC,则图中与∠1相等的角(∠1除外)共有( )
A.4个
B.5个
C.6个
D.7个
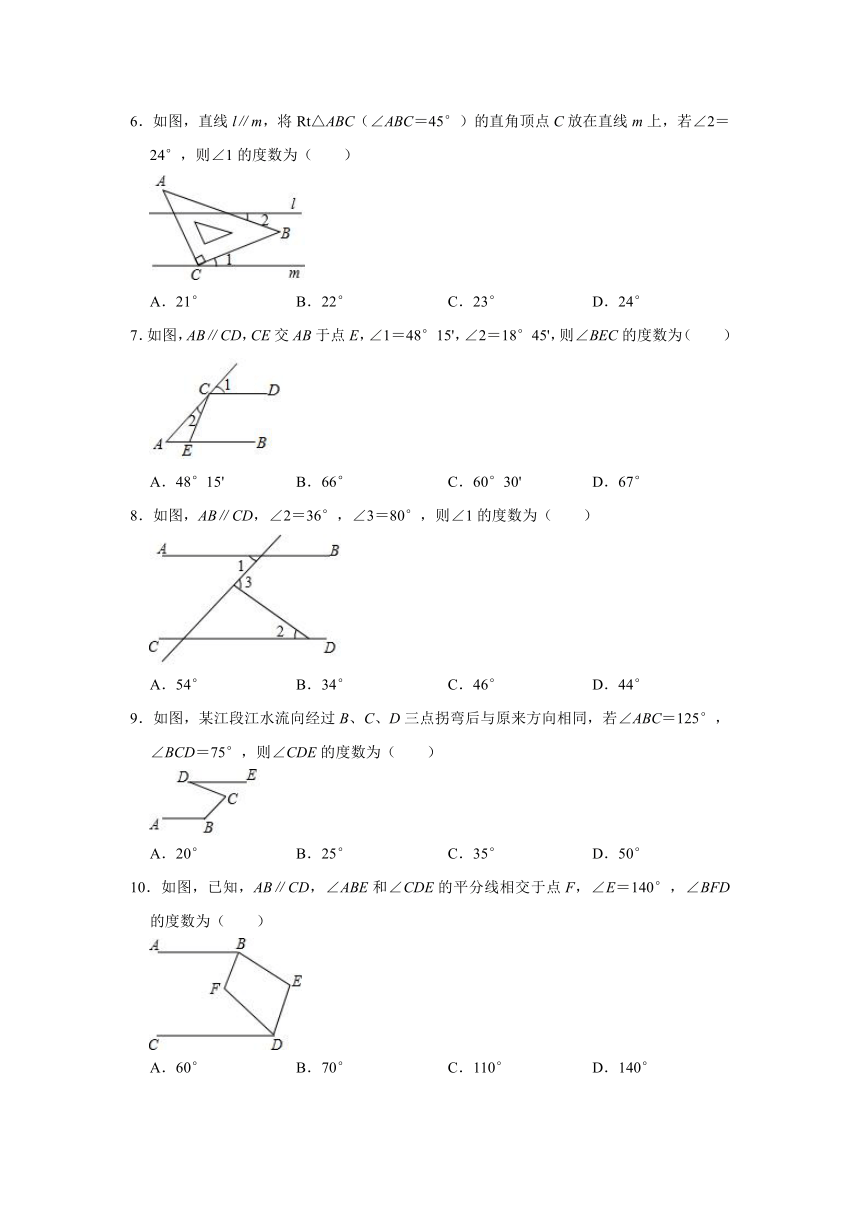
6.如图,直线l∥m,将Rt△ABC(∠ABC=45°)的直角顶点C放在直线m上,若∠2=24°,则∠1的度数为( )
A.21°
B.22°
C.23°
D.24°
7.如图,AB∥CD,CE交AB于点E,∠1=48°15',∠2=18°45',则∠BEC的度数为( )
A.48°15'
B.66°
C.60°30'
D.67°
8.如图,AB∥CD,∠2=36°,∠3=80°,则∠1的度数为( )
A.54°
B.34°
C.46°
D.44°
9.如图,某江段江水流向经过B、C、D三点拐弯后与原来方向相同,若∠ABC=125°,∠BCD=75°,则∠CDE的度数为( )
A.20°
B.25°
C.35°
D.50°
10.如图,已知,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠E=140°,∠BFD的度数为( )
A.60°
B.70°
C.110°
D.140°
11.如图,直线a∥b,∠B=22°,∠C=50°,则∠A的度数为
°.
12.如图,梯子的各条横档互相平行,若∠1﹣∠2=30°,则∠3=
.
13.如图,∠ABC=∠ADC,AB∥CD,E为射线BC上一点,AE平分∠BAD,AE、CD交于点F,点E在线段BC延长线上时,连接DE,若∠DCB+2∠CDE=180°,∠B=24°,则∠DEF的度数为
.
14.已知如图,AB∥CD,∠A=130°,∠D=25°,那么∠AED=
°.
15.如图,已知a∥b,∠2=93°25′,∠3=140°,则∠1的度数为
.
16.如图(1)是长方形纸带,∠DEF=20°,将纸带沿EF折叠图(2)形状,则∠FGD等于
度.
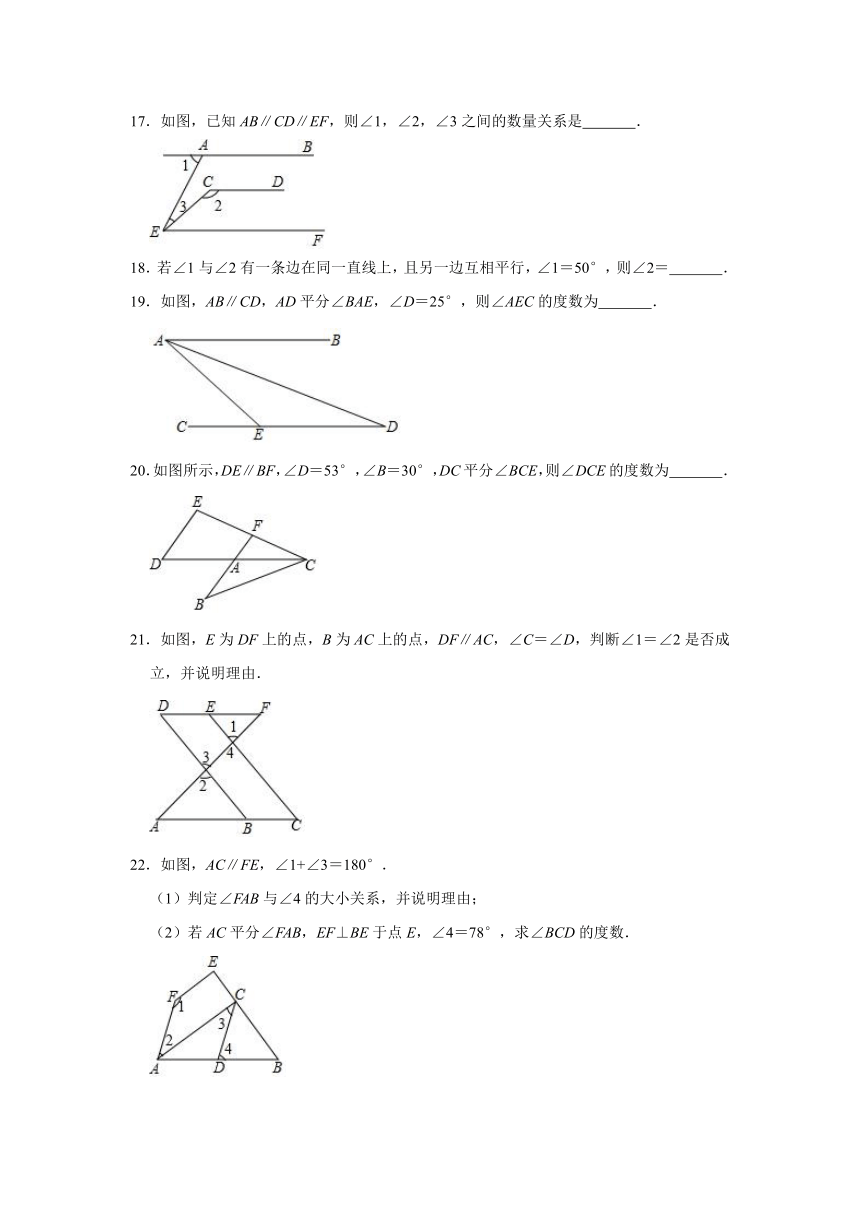
17.如图,已知AB∥CD∥EF,则∠1,∠2,∠3之间的数量关系是
.
18.若∠1与∠2有一条边在同一直线上,且另一边互相平行,∠1=50°,则∠2=
.
19.如图,AB∥CD,AD平分∠BAE,∠D=25°,则∠AEC的度数为
.
20.如图所示,DE∥BF,∠D=53°,∠B=30°,DC平分∠BCE,则∠DCE的度数为
.
21.如图,E为DF上的点,B为AC上的点,DF∥AC,∠C=∠D,判断∠1=∠2是否成立,并说明理由.
22.如图,AC∥FE,∠1+∠3=180°.
(1)判定∠FAB与∠4的大小关系,并说明理由;
(2)若AC平分∠FAB,EF⊥BE于点E,∠4=78°,求∠BCD的度数.
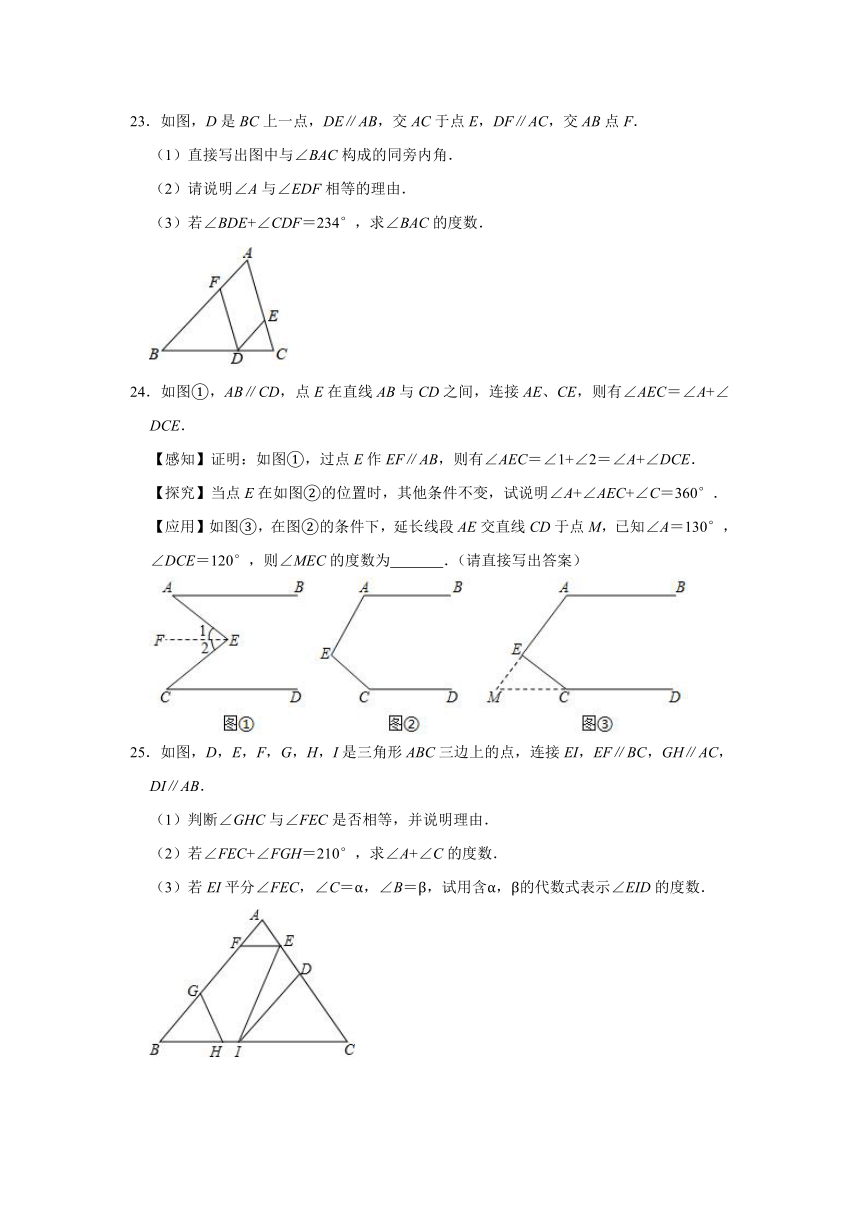
23.如图,D是BC上一点,DE∥AB,交AC于点E,DF∥AC,交AB点F.
(1)直接写出图中与∠BAC构成的同旁内角.
(2)请说明∠A与∠EDF相等的理由.
(3)若∠BDE+∠CDF=234°,求∠BAC的度数.
24.如图①,AB∥CD,点E在直线AB与CD之间,连接AE、CE,则有∠AEC=∠A+∠DCE.
【感知】证明:如图①,过点E作EF∥AB,则有∠AEC=∠1+∠2=∠A+∠DCE.
【探究】当点E在如图②的位置时,其他条件不变,试说明∠A+∠AEC+∠C=360°.
【应用】如图③,在图②的条件下,延长线段AE交直线CD于点M,已知∠A=130°,∠DCE=120°,则∠MEC的度数为
.(请直接写出答案)
25.如图,D,E,F,G,H,I是三角形ABC三边上的点,连接EI,EF∥BC,GH∥AC,DI∥AB.
(1)判断∠GHC与∠FEC是否相等,并说明理由.
(2)若∠FEC+∠FGH=210°,求∠A+∠C的度数.
(3)若EI平分∠FEC,∠C=α,∠B=β,试用含α,β的代数式表示∠EID的度数.
26.已知,AB∥CD,E为直线AB上一点,F为直线CD上一点,EF交AD于点G,且∠AEF=∠C.
(1)如图1,求证:∠C+∠ADC=∠AGF;
(2)如图2,∠C、∠ADC和∠AGF的数量关系是
;
(3)如图3,在(2)的条件下,连接BF,DE相交于点H,∠AED和∠BFC的平分线交于点P,若FC恰好平分∠BFG,∠C=60°,∠P=2∠HEG,求∠EHF的度数.
参考答案
1.解:如图,延长ED交BC于F,
∵BA∥DE,
∴∠BFD=∠B=120°,∠CFD=60°,
又∵∠CDE是△CFD的外角,
∴∠C=∠CDE﹣∠DFC=135°﹣60°=75°.
故选:A.
2.解:设∠β为x,则∠α为3x﹣40°,
若两角互补,则x+3x﹣40°=180°,解得x=55°,∠α=125°;
若两角相等,则x=3x﹣40°,解得x=20°,∠α=20°.
故选:C.
3.解:如图,过E作EG∥AB,
∵AB∥CD,
∴AB∥CD∥EG,
∴∠GEF=∠DHF=∠C+∠F,
∠A+∠AEG=180°,
∴∠A+∠AEF﹣∠GEF=180°,
即∠A+∠AEF﹣∠C﹣∠F=180°,
故选:B.
4.解:如图,∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,
∴∠BEF=∠1+∠F=50°,
∵AB∥CD,
∴∠2=∠BEF=50°,
故选:C.
5.解:∵AD∥EF∥BC,BD∥GF,
∴∠1=∠ADB=∠DBC=∠FGC=∠EFG,∠1=∠EHB,
又∵BD平分∠ADC,
∴∠ADB=∠CDB=∠CFG,
∴图中与∠1相等的角(∠1除外)共有7个,
故选:D.
6.解:如图,
∵∠2=24°,
∴∠3=∠2=24°.
∵∠A=45°,
∴∠4=180°﹣45°﹣24°=111°.
∵直线l∥m,
∴∠ACD=111°,
∴∠1=111°﹣90°=21°.
故选:A.
7.解:∵AB∥CD,
∴∠1=∠A=48°15',
又∵∠2=18°45',
∴∠BEC=∠A+∠2=67°,
故选:D.
8.解:如图,∵AB∥CD,
∴∠1=∠4,
∵∠3=∠4+∠2,∠2=36°,∠3=80°,
∴∠4=44°,
∴∠1=44°,
故选:D.
9.解:由题意得,AB∥DE,
如图,过点C作CF∥AB,则CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=180°﹣125°=55°,
∴∠DCF=75°﹣55°=20°,
∴∠CDE=∠DCF=20°.
故选:A.
10.解:过点E作EG∥AB,如图所示.
则可得∠ABE+∠BEG=180°,∠GED+∠EDC=180°,
∴∠ABE+∠CDE+∠BED=360°;
又∵∠BED=140°,
∴∠ABE+∠CDE=220°.
∵∠ABE和∠CDE的平分线相交于F,
∴∠FBE+∠EDF=(∠ABE+∠CDE)÷2=110°,
∵四边形的BFDE的内角和为360°,
∴∠BFD=110°.
故选:C.
11.解:如图,
∵a∥b,
∴∠1=∠C=50°,
又∠1=∠A+∠B,
∴∠A=∠1﹣∠B=50°﹣22°=28°,
故答案为:28.
12.解:∵AB∥CD,
∴∠1=∠3,
又∵∠1﹣∠2=30°,
∴∠2=∠1﹣30°,
∴∠2=∠3﹣30°,
又∵∠3+∠2=180°,
∴∠3+∠3﹣30°=180°,
∴∠3=105°,
故答案为:105°.
13.解:设∠CDE=x,
∵∠BCD+2∠CDE=180°,
∴∠DCB=180°﹣2x,
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,∠ABC=∠ADC=2x°,
∵∠B=24°,
∴x=12°,
∴∠ADE=36°,
∵AE平分∠BAD,AB∥CD,∠B=24°,
∴∠DAE=78°,
∴∠DEF=180°﹣∠DAE﹣∠ADE=180°﹣78°﹣36°=66°.
故答案为:66°.
14.解:如图:过E作EF∥AB,则AB∥EF∥CD,
∵∠A=130°,
∴∠1=180°﹣130°=50°,
∵∠D=25°,
∴∠2=∠D=25°,
∴∠AED=50°+25°=75°,
故答案为:75.
15.解:如图,∵∠3=140°,∠3+∠4=180°,
∴∠4=40°,
∵∠2=93°25′,∠2=∠5+∠4,
∴∠5=53°25′,
∵a∥b,
∴∠1+∠5=180°,
∴∠1=126°35′.
故答案为:126°35′.
16.解:根据折叠可知:
∠AEG=180°﹣20°×2=140°,
∵AE∥BF,
∴∠EGB=180°﹣∠AEG=40°,
∴∠FGD=40°.
故答案为:40.
17.解:∵CD∥EF,
∴∠2+∠CEF=180°,
∵AB∥EF,
∴∠1=∠3+∠CEF,
∴∠CEF=∠1﹣∠3,
∴∠2+∠1﹣∠3=180°,
即∠1﹣∠3+∠2=180°.
故答案为:∠1﹣∠3+∠2=180°.
18.解:如图:当α=∠2时,∠2=∠1=50°,
当β=∠2时,∠β=180°﹣50°=130°.
故答案为:50°或130°.
19.解:∵AB∥CD,AD平分∠BAE,∠D=25°,
∴∠BAD=∠ADE,∠BAD=∠EAD,
∴∠ADE=∠EAD=25°,
∵∠AEC=∠ADE+∠EAD,
∴∠AEC=50°,
故答案为:50°.
20.解:∵DE∥BF,∠D=53°,
∴∠FAC=∠D=53°,
∵∠B=30°,
∴∠ACB=23°,
∵DC平分∠BCE,
∴∠DCE=23°.
故答案为:23°.
21.解:∠1=∠2成立.
理由:∵DF∥AC,
∴∠C=∠CEF,
又∵∠C=∠D,
∴∠CEF=∠D,
∴BD∥CE,
∴∠3=∠4,
又∵∠3=∠2,∠4=∠1,
∴∠1=∠2.
22.解:(1)∠FAB=∠4,
理由如下:
∵AC∥EF,
∴∠1+∠2=180°,
又∵∠1+∠3=180°,
∴∠2=∠3,
∴FA∥CD,
∴∠FAB=∠4;
(2)∵AC平分∠FAB,
∴∠2=∠CAD,
∵∠2=∠3,
∴∠CAD=∠3,
∵∠4=∠3+∠CAD,
∴,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠3=51°.
23.解:(1)∠BAC的同旁内角有:∠AFD,∠AED,∠C,∠B;
(2)∵DE∥AB,
∴∠BAC=∠DEC,
∵DF∥AC,
∴∠EDF=∠DEC,
∴∠BAC=∠EDF;
(3)∵∠BDE+∠CDF=234°,
∴∠BDE+∠EDC+∠EDF=234°,
即180°+∠EDF=234°,
∴∠EDF=54°,
∴∠BAC=54°.
24.【感知】证明:如图①,
过点E作EF∥AB,
∴∠A=∠1,
∵AB∥CD,
∵EF∥AB,
∴CD∥EF,
∴∠2=∠DCE,
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠DCE(等量代换),
【探究】证明:过点E作EF∥AB,如图②所示:
∵AB∥CD,
∴EF∥CD,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°;
【应用】解:同【探究】得:∠A+∠AEC+∠DCE=360°,
∴∠AEC=360°﹣∠A﹣∠DCE=360°﹣130°﹣120°=110°,
∴∠MEC=180°﹣∠AEC=180°﹣110°=70°,
故答案为:70°.
25.解:(1)∠GHC=∠FEC,
理由:∵EF∥BC,
∴∠FEC+∠C=180°,
∵GH∥AC,
∴∠GHC+∠C=180°,
∴∠GHC=∠FEC;
(2)∵GH∥AC,
∴∠FGH+∠A=180°,
∵EF∥BC,
∴∠FEC+∠C=180°,
∴∠FGH+∠FEC+∠C+∠A=360°,
∵∠FEC+∠FGH=210°,
∴∠A+∠C=360°﹣210°=150°;
(3)∵EF∥BC,
∴∠FEC+∠C=180°,∠FEI=∠EIC,
∴∠FEC=180°﹣α,
∵EI平分∠FEC,
∴∠FEI=∠FEC=90°﹣,
∴∠FEI=∠EIC=90°﹣,
∵DI∥AB,
∴∠DIC=∠B=β,
∴∠EID=∠EIC﹣∠DIC=90°﹣﹣β.
26.(1)证明:∵AB∥CD,
∴∠AEF=∠EFD,
∵∠AEF=∠C,
∴∠C=∠EFD,
∵∠EFD+∠ADC=∠AGF,
∴∠C+∠ADC=∠AGF;
(2)解:∵AB∥CD,
∴∠AEF=∠CFG,
∵∠AEF=∠C,
∴∠C=∠CFG,
∵∠CFG+∠FDG+∠AGF=180°,∠FDG=∠ADC,
∴∠C+∠ADC+∠AGF=180°;
故答案为:180°;
(3)解:设∠HEG=α,则∠P=2α,
∵∠C=60°,∠AEF=∠C,
∴∠AEF=60°,
∴∠AED=60°﹣α,
∵EP平分∠AED,
∴∠PED=30°﹣α,
∵∠AEF=60°,
∵AB∥CD,
∴∠CFG=60°,
∵FC平分∠BFG,
∴∠CFB=60°,∠BFE=60°,
∵FP平分∠PFC,
∴∠PFC=30°,
∴∠PFE=90°,
在△PEF中,∠EPF+∠PFE+∠PEF=180°,
∴2α+α+30°﹣α+90°=180°,解得:α=24°,
∴∠EHF=180°﹣∠DEF﹣∠BFE=180°﹣24°﹣60°=96°
1.如图是郝老师的某次行车路线,总共拐了三次弯,最后行车路线与开始的路线是平行的,已知第一次转过的角度120°,第三次转过的角度135°,则第二次拐弯的角度是( )
A.75°
B.120°
C.135°
D.无法确定
2.如果∠α与∠β的两边分别平行,∠α比∠β的3倍少40°,则∠α的度数为( )
A.20°
B.125°
C.20°或125°
D.35°或110
3.如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )
A.∠A=∠C+∠E+∠F
B.∠A+∠E﹣∠C﹣∠F=180°
C.∠A﹣∠E+∠C+∠F=90°
D.∠A+∠E+∠C+∠F=360°
4.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A.30°
B.40°
C.50°
D.60°
5.如图,已知AD∥EF∥BC,BD∥GF,且BD平分∠ADC,则图中与∠1相等的角(∠1除外)共有( )
A.4个
B.5个
C.6个
D.7个
6.如图,直线l∥m,将Rt△ABC(∠ABC=45°)的直角顶点C放在直线m上,若∠2=24°,则∠1的度数为( )
A.21°
B.22°
C.23°
D.24°
7.如图,AB∥CD,CE交AB于点E,∠1=48°15',∠2=18°45',则∠BEC的度数为( )
A.48°15'
B.66°
C.60°30'
D.67°
8.如图,AB∥CD,∠2=36°,∠3=80°,则∠1的度数为( )
A.54°
B.34°
C.46°
D.44°
9.如图,某江段江水流向经过B、C、D三点拐弯后与原来方向相同,若∠ABC=125°,∠BCD=75°,则∠CDE的度数为( )
A.20°
B.25°
C.35°
D.50°
10.如图,已知,AB∥CD,∠ABE和∠CDE的平分线相交于点F,∠E=140°,∠BFD的度数为( )
A.60°
B.70°
C.110°
D.140°
11.如图,直线a∥b,∠B=22°,∠C=50°,则∠A的度数为
°.
12.如图,梯子的各条横档互相平行,若∠1﹣∠2=30°,则∠3=
.
13.如图,∠ABC=∠ADC,AB∥CD,E为射线BC上一点,AE平分∠BAD,AE、CD交于点F,点E在线段BC延长线上时,连接DE,若∠DCB+2∠CDE=180°,∠B=24°,则∠DEF的度数为
.
14.已知如图,AB∥CD,∠A=130°,∠D=25°,那么∠AED=
°.
15.如图,已知a∥b,∠2=93°25′,∠3=140°,则∠1的度数为
.
16.如图(1)是长方形纸带,∠DEF=20°,将纸带沿EF折叠图(2)形状,则∠FGD等于
度.
17.如图,已知AB∥CD∥EF,则∠1,∠2,∠3之间的数量关系是
.
18.若∠1与∠2有一条边在同一直线上,且另一边互相平行,∠1=50°,则∠2=
.
19.如图,AB∥CD,AD平分∠BAE,∠D=25°,则∠AEC的度数为
.
20.如图所示,DE∥BF,∠D=53°,∠B=30°,DC平分∠BCE,则∠DCE的度数为
.
21.如图,E为DF上的点,B为AC上的点,DF∥AC,∠C=∠D,判断∠1=∠2是否成立,并说明理由.
22.如图,AC∥FE,∠1+∠3=180°.
(1)判定∠FAB与∠4的大小关系,并说明理由;
(2)若AC平分∠FAB,EF⊥BE于点E,∠4=78°,求∠BCD的度数.
23.如图,D是BC上一点,DE∥AB,交AC于点E,DF∥AC,交AB点F.
(1)直接写出图中与∠BAC构成的同旁内角.
(2)请说明∠A与∠EDF相等的理由.
(3)若∠BDE+∠CDF=234°,求∠BAC的度数.
24.如图①,AB∥CD,点E在直线AB与CD之间,连接AE、CE,则有∠AEC=∠A+∠DCE.
【感知】证明:如图①,过点E作EF∥AB,则有∠AEC=∠1+∠2=∠A+∠DCE.
【探究】当点E在如图②的位置时,其他条件不变,试说明∠A+∠AEC+∠C=360°.
【应用】如图③,在图②的条件下,延长线段AE交直线CD于点M,已知∠A=130°,∠DCE=120°,则∠MEC的度数为
.(请直接写出答案)
25.如图,D,E,F,G,H,I是三角形ABC三边上的点,连接EI,EF∥BC,GH∥AC,DI∥AB.
(1)判断∠GHC与∠FEC是否相等,并说明理由.
(2)若∠FEC+∠FGH=210°,求∠A+∠C的度数.
(3)若EI平分∠FEC,∠C=α,∠B=β,试用含α,β的代数式表示∠EID的度数.
26.已知,AB∥CD,E为直线AB上一点,F为直线CD上一点,EF交AD于点G,且∠AEF=∠C.
(1)如图1,求证:∠C+∠ADC=∠AGF;
(2)如图2,∠C、∠ADC和∠AGF的数量关系是
;
(3)如图3,在(2)的条件下,连接BF,DE相交于点H,∠AED和∠BFC的平分线交于点P,若FC恰好平分∠BFG,∠C=60°,∠P=2∠HEG,求∠EHF的度数.
参考答案
1.解:如图,延长ED交BC于F,
∵BA∥DE,
∴∠BFD=∠B=120°,∠CFD=60°,
又∵∠CDE是△CFD的外角,
∴∠C=∠CDE﹣∠DFC=135°﹣60°=75°.
故选:A.
2.解:设∠β为x,则∠α为3x﹣40°,
若两角互补,则x+3x﹣40°=180°,解得x=55°,∠α=125°;
若两角相等,则x=3x﹣40°,解得x=20°,∠α=20°.
故选:C.
3.解:如图,过E作EG∥AB,
∵AB∥CD,
∴AB∥CD∥EG,
∴∠GEF=∠DHF=∠C+∠F,
∠A+∠AEG=180°,
∴∠A+∠AEF﹣∠GEF=180°,
即∠A+∠AEF﹣∠C﹣∠F=180°,
故选:B.
4.解:如图,∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,
∴∠BEF=∠1+∠F=50°,
∵AB∥CD,
∴∠2=∠BEF=50°,
故选:C.
5.解:∵AD∥EF∥BC,BD∥GF,
∴∠1=∠ADB=∠DBC=∠FGC=∠EFG,∠1=∠EHB,
又∵BD平分∠ADC,
∴∠ADB=∠CDB=∠CFG,
∴图中与∠1相等的角(∠1除外)共有7个,
故选:D.
6.解:如图,
∵∠2=24°,
∴∠3=∠2=24°.
∵∠A=45°,
∴∠4=180°﹣45°﹣24°=111°.
∵直线l∥m,
∴∠ACD=111°,
∴∠1=111°﹣90°=21°.
故选:A.
7.解:∵AB∥CD,
∴∠1=∠A=48°15',
又∵∠2=18°45',
∴∠BEC=∠A+∠2=67°,
故选:D.
8.解:如图,∵AB∥CD,
∴∠1=∠4,
∵∠3=∠4+∠2,∠2=36°,∠3=80°,
∴∠4=44°,
∴∠1=44°,
故选:D.
9.解:由题意得,AB∥DE,
如图,过点C作CF∥AB,则CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=180°﹣125°=55°,
∴∠DCF=75°﹣55°=20°,
∴∠CDE=∠DCF=20°.
故选:A.
10.解:过点E作EG∥AB,如图所示.
则可得∠ABE+∠BEG=180°,∠GED+∠EDC=180°,
∴∠ABE+∠CDE+∠BED=360°;
又∵∠BED=140°,
∴∠ABE+∠CDE=220°.
∵∠ABE和∠CDE的平分线相交于F,
∴∠FBE+∠EDF=(∠ABE+∠CDE)÷2=110°,
∵四边形的BFDE的内角和为360°,
∴∠BFD=110°.
故选:C.
11.解:如图,
∵a∥b,
∴∠1=∠C=50°,
又∠1=∠A+∠B,
∴∠A=∠1﹣∠B=50°﹣22°=28°,
故答案为:28.
12.解:∵AB∥CD,
∴∠1=∠3,
又∵∠1﹣∠2=30°,
∴∠2=∠1﹣30°,
∴∠2=∠3﹣30°,
又∵∠3+∠2=180°,
∴∠3+∠3﹣30°=180°,
∴∠3=105°,
故答案为:105°.
13.解:设∠CDE=x,
∵∠BCD+2∠CDE=180°,
∴∠DCB=180°﹣2x,
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,∠ABC=∠ADC=2x°,
∵∠B=24°,
∴x=12°,
∴∠ADE=36°,
∵AE平分∠BAD,AB∥CD,∠B=24°,
∴∠DAE=78°,
∴∠DEF=180°﹣∠DAE﹣∠ADE=180°﹣78°﹣36°=66°.
故答案为:66°.
14.解:如图:过E作EF∥AB,则AB∥EF∥CD,
∵∠A=130°,
∴∠1=180°﹣130°=50°,
∵∠D=25°,
∴∠2=∠D=25°,
∴∠AED=50°+25°=75°,
故答案为:75.
15.解:如图,∵∠3=140°,∠3+∠4=180°,
∴∠4=40°,
∵∠2=93°25′,∠2=∠5+∠4,
∴∠5=53°25′,
∵a∥b,
∴∠1+∠5=180°,
∴∠1=126°35′.
故答案为:126°35′.
16.解:根据折叠可知:
∠AEG=180°﹣20°×2=140°,
∵AE∥BF,
∴∠EGB=180°﹣∠AEG=40°,
∴∠FGD=40°.
故答案为:40.
17.解:∵CD∥EF,
∴∠2+∠CEF=180°,
∵AB∥EF,
∴∠1=∠3+∠CEF,
∴∠CEF=∠1﹣∠3,
∴∠2+∠1﹣∠3=180°,
即∠1﹣∠3+∠2=180°.
故答案为:∠1﹣∠3+∠2=180°.
18.解:如图:当α=∠2时,∠2=∠1=50°,
当β=∠2时,∠β=180°﹣50°=130°.
故答案为:50°或130°.
19.解:∵AB∥CD,AD平分∠BAE,∠D=25°,
∴∠BAD=∠ADE,∠BAD=∠EAD,
∴∠ADE=∠EAD=25°,
∵∠AEC=∠ADE+∠EAD,
∴∠AEC=50°,
故答案为:50°.
20.解:∵DE∥BF,∠D=53°,
∴∠FAC=∠D=53°,
∵∠B=30°,
∴∠ACB=23°,
∵DC平分∠BCE,
∴∠DCE=23°.
故答案为:23°.
21.解:∠1=∠2成立.
理由:∵DF∥AC,
∴∠C=∠CEF,
又∵∠C=∠D,
∴∠CEF=∠D,
∴BD∥CE,
∴∠3=∠4,
又∵∠3=∠2,∠4=∠1,
∴∠1=∠2.
22.解:(1)∠FAB=∠4,
理由如下:
∵AC∥EF,
∴∠1+∠2=180°,
又∵∠1+∠3=180°,
∴∠2=∠3,
∴FA∥CD,
∴∠FAB=∠4;
(2)∵AC平分∠FAB,
∴∠2=∠CAD,
∵∠2=∠3,
∴∠CAD=∠3,
∵∠4=∠3+∠CAD,
∴,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠3=51°.
23.解:(1)∠BAC的同旁内角有:∠AFD,∠AED,∠C,∠B;
(2)∵DE∥AB,
∴∠BAC=∠DEC,
∵DF∥AC,
∴∠EDF=∠DEC,
∴∠BAC=∠EDF;
(3)∵∠BDE+∠CDF=234°,
∴∠BDE+∠EDC+∠EDF=234°,
即180°+∠EDF=234°,
∴∠EDF=54°,
∴∠BAC=54°.
24.【感知】证明:如图①,
过点E作EF∥AB,
∴∠A=∠1,
∵AB∥CD,
∵EF∥AB,
∴CD∥EF,
∴∠2=∠DCE,
∵∠AEC=∠1+∠2,
∴∠AEC=∠A+∠DCE(等量代换),
【探究】证明:过点E作EF∥AB,如图②所示:
∵AB∥CD,
∴EF∥CD,
∴∠A+∠AEF=180°,∠C+∠CEF=180°,
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°;
【应用】解:同【探究】得:∠A+∠AEC+∠DCE=360°,
∴∠AEC=360°﹣∠A﹣∠DCE=360°﹣130°﹣120°=110°,
∴∠MEC=180°﹣∠AEC=180°﹣110°=70°,
故答案为:70°.
25.解:(1)∠GHC=∠FEC,
理由:∵EF∥BC,
∴∠FEC+∠C=180°,
∵GH∥AC,
∴∠GHC+∠C=180°,
∴∠GHC=∠FEC;
(2)∵GH∥AC,
∴∠FGH+∠A=180°,
∵EF∥BC,
∴∠FEC+∠C=180°,
∴∠FGH+∠FEC+∠C+∠A=360°,
∵∠FEC+∠FGH=210°,
∴∠A+∠C=360°﹣210°=150°;
(3)∵EF∥BC,
∴∠FEC+∠C=180°,∠FEI=∠EIC,
∴∠FEC=180°﹣α,
∵EI平分∠FEC,
∴∠FEI=∠FEC=90°﹣,
∴∠FEI=∠EIC=90°﹣,
∵DI∥AB,
∴∠DIC=∠B=β,
∴∠EID=∠EIC﹣∠DIC=90°﹣﹣β.
26.(1)证明:∵AB∥CD,
∴∠AEF=∠EFD,
∵∠AEF=∠C,
∴∠C=∠EFD,
∵∠EFD+∠ADC=∠AGF,
∴∠C+∠ADC=∠AGF;
(2)解:∵AB∥CD,
∴∠AEF=∠CFG,
∵∠AEF=∠C,
∴∠C=∠CFG,
∵∠CFG+∠FDG+∠AGF=180°,∠FDG=∠ADC,
∴∠C+∠ADC+∠AGF=180°;
故答案为:180°;
(3)解:设∠HEG=α,则∠P=2α,
∵∠C=60°,∠AEF=∠C,
∴∠AEF=60°,
∴∠AED=60°﹣α,
∵EP平分∠AED,
∴∠PED=30°﹣α,
∵∠AEF=60°,
∵AB∥CD,
∴∠CFG=60°,
∵FC平分∠BFG,
∴∠CFB=60°,∠BFE=60°,
∵FP平分∠PFC,
∴∠PFC=30°,
∴∠PFE=90°,
在△PEF中,∠EPF+∠PFE+∠PEF=180°,
∴2α+α+30°﹣α+90°=180°,解得:α=24°,
∴∠EHF=180°﹣∠DEF﹣∠BFE=180°﹣24°﹣60°=96°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
