3.1用表格表示变量之间关系-2020-2021学年北师大版七年级数学下册同步提升训练试卷(Word版含答案)
文档属性
| 名称 | 3.1用表格表示变量之间关系-2020-2021学年北师大版七年级数学下册同步提升训练试卷(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 116.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 14:48:45 | ||
图片预览


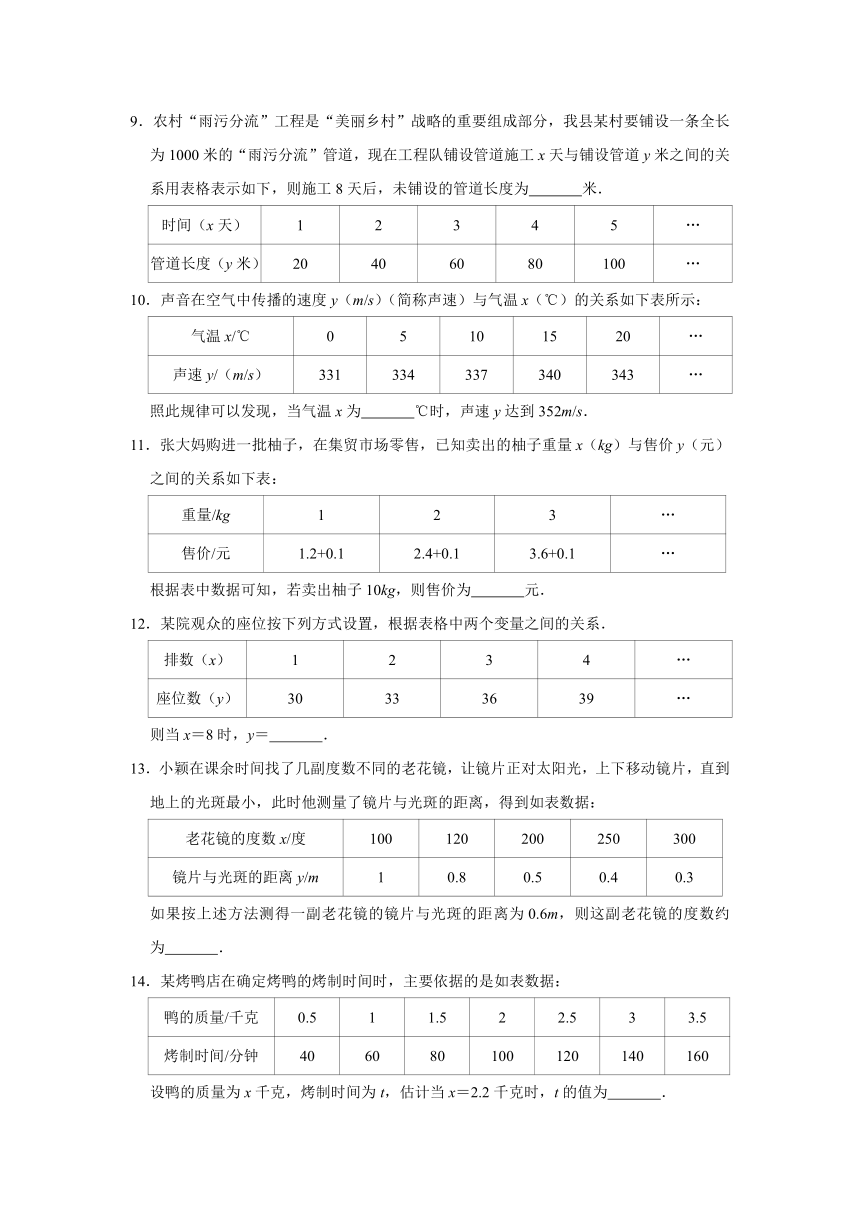

文档简介
2021年度北师大版七年级数学下册《3.1用表格表示变量之间关系》同步提升训练(附答案)
1.在某一阶段,某商品的销售量与销售价之间存在如表关系:
销售价/元
90
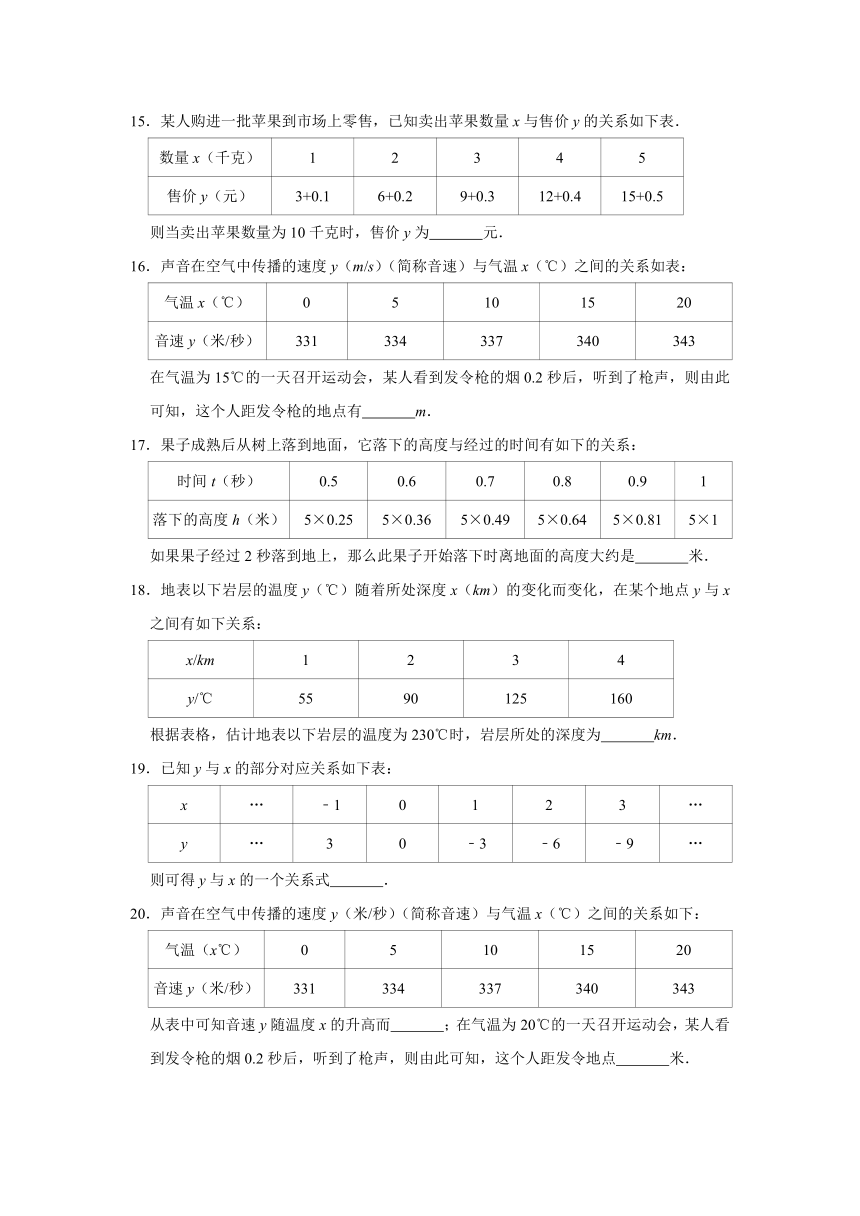
100
110
120
130
140
销售量/件
90
80
70
60
50
40
设该商品的销售价为x元,销售量为y件,估计:当x=127时,y的值为( )
A.63
B.59
C.53
D.43
2.一个蓄水池有水50m3,打开放水闸门放水,水池里的水和放水时间的关系如表,下面说法不正确的是( )
放水时间(分)
1
2
3
4
…
水池中水量(m3)
48
46
44
42
…
A.水池里的水量是自变量,放水时间是因变量
B.每分钟放水2m3
C.放水10分钟后,水池里还有水30m3
D.放水25分钟,水池里的水全部放完
3.在实验课上,小亮利用同一块木板测得小车从不同高度(h)与下滑的时间(t)的关系如下表:
支撑物高h(cm)
10
20
30
40
50
…
下滑时间t(s)
3.25
3.01
2.81
2.66
2.56
…
以下结论错误的是( )
A.当h=40时,t约2.66秒
B.随高度增加,下滑时间越来越短
C.估计当h=80cm时,t一定小于2.56秒
D.高度每增加了10cm,时间就会减少0.24秒
4.已知声音在空气中的传播速度与空气的温度有关,在一定范围内,其关系如表所示,下列说法错误的是( )
温度/℃
﹣20
﹣10
0
10
20
30
传播速度/(m/s)
318
324
330
336
342
348
A.自变量是温度,因变量是传播速度
B.温度越高,传播速度越快
C.当温度为10℃时,声音5s可以传播1650m
D.温度每升高10℃,传播速度增加6m/s
5.某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦?时)
1
2
3
4
…
应缴电费(元)
0.55
1.10
1.65
2.20
…
A.用电量每增加1千瓦?时,电费增加0.55元
B.若用电量为8千瓦?时,则应缴电费4.4元
C.若应缴电费为2.75元,则用电量为6千瓦?时
D.应缴电费随用电量的增加而增加
6.研究表明,当每公顷钾肥和磷肥的施用量一定时,氮肥施用量与土豆的产量有如表所示的关系:
氮肥施用量/千克
0
34
67
101
135
202
259
336
404
471
土豆产量/吨
15.18
21.36
25.72
32.29
34.05
39.45
43.15
43.46
40.83
30.75
下列说法错误的是( )
A.氮肥施用量是自变量,土豆产量是因变量
B.当氮肥的施用量是101千克/公顷时,土豆的产量是32.29吨/公顷
C.如果不施氮肥,土豆的产量是15.18吨/公顷
D.氮肥施用量404千克/公顷比氮肥施用量336千克/公顷时的土豆的产量更高
7.在某一阶段,某商品的销售量与销售价之间存在如表关系:
销售价/元
90
100
110
120
130
140
销售量/件
90
80
70
60
50
40
设该商品的销售价为x元,销售量为y件,估计当x=126时,y的值为( )
A.64
B.57
C.54
D.47
8.某汽车生产厂家对其生产的一款汽车进行耗油量试验.在试验过程中,汽车一直匀速行驶,该汽车油箱中的余油量y(升)与汽车的行驶时间t(小时)之间的关系如表:
t(小时)
0
1
2
3
y(升)
120
112
104
96
则用关系式法表示因变量y(升)与自变量t(小时)之间的关系为:
.
9.农村“雨污分流”工程是“美丽乡村”战略的重要组成部分,我县某村要铺设一条全长为1000米的“雨污分流”管道,现在工程队铺设管道施工x天与铺设管道y米之间的关系用表格表示如下,则施工8天后,未铺设的管道长度为
米.
时间(x天)
1
2
3
4
5
…
管道长度(y米)
20
40
60
80
100
…
10.声音在空气中传播的速度y(m/s)(简称声速)与气温x(℃)的关系如下表所示:
气温x/℃
0
5
10
15
20
…
声速y/(m/s)
331
334
337
340
343
…
照此规律可以发现,当气温x为
℃时,声速y达到352m/s.
11.张大妈购进一批柚子,在集贸市场零售,已知卖出的柚子重量x(kg)与售价y(元)之间的关系如下表:
重量/kg
1
2
3
…
售价/元
1.2+0.1
2.4+0.1
3.6+0.1
…
根据表中数据可知,若卖出柚子10kg,则售价为
元.
12.某院观众的座位按下列方式设置,根据表格中两个变量之间的关系.
排数(x)
1
2
3
4
…
座位数(y)
30
33
36
39
…
则当x=8时,y=
.
13.小颖在课余时间找了几副度数不同的老花镜,让镜片正对太阳光,上下移动镜片,直到地上的光斑最小,此时他测量了镜片与光斑的距离,得到如表数据:
老花镜的度数x/度
100
120
200
250
300
镜片与光斑的距离y/m
1
0.8
0.5
0.4
0.3
如果按上述方法测得一副老花镜的镜片与光斑的距离为0.6m,则这副老花镜的度数约为
.
14.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是如表数据:
鸭的质量/千克
0.5
1
1.5
2
2.5
3
3.5
烤制时间/分钟
40
60
80
100
120
140
160
设鸭的质量为x千克,烤制时间为t,估计当x=2.2千克时,t的值为
.
15.某人购进一批苹果到市场上零售,已知卖出苹果数量x与售价y的关系如下表.
数量x(千克)
1
2
3
4
5
售价y(元)
3+0.1
6+0.2
9+0.3
12+0.4
15+0.5
则当卖出苹果数量为10千克时,售价y为
元.
16.声音在空气中传播的速度y(m/s)(简称音速)与气温x(℃)之间的关系如表:
气温x(℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
在气温为15℃的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,则由此可知,这个人距发令枪的地点有
m.
17.果子成熟后从树上落到地面,它落下的高度与经过的时间有如下的关系:
时间t(秒)
0.5
0.6
0.7
0.8
0.9
1
落下的高度h(米)
5×0.25
5×0.36
5×0.49
5×0.64
5×0.81
5×1
如果果子经过2秒落到地上,那么此果子开始落下时离地面的高度大约是
米.
18.地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间有如下关系:
x/km
1
2
3
4
y/℃
55
90
125
160
根据表格,估计地表以下岩层的温度为230℃时,岩层所处的深度为
km.
19.已知y与x的部分对应关系如下表:
x
…
﹣1
0
1
2
3
…
y
…
3
0
﹣3
﹣6
﹣9
…
则可得y与x的一个关系式
.
20.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下:
气温(x℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
从表中可知音速y随温度x的升高而
;在气温为20℃的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,则由此可知,这个人距发令地点
米.
21.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下.一辆汽车停在路边,其正前方有一座山崖,驾驶员按响喇叭,4s后听到回声,若当时的气温为25℃,则由此可知,汽车距山崖
米.
气温x(℃)
0
5
10
15
20
25
音速y(米/秒)
331
334
337
340
343
346
22.为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成如表:
汽车行驶时间t(小时)
0
1
2
3
…
油箱剩余油量Q(升)
100
94
88
82
…
(1)如表反映的两个变量中,自变量是
,因变量是
.
(2)根据表可知,汽车行驶3小时时,该车油箱的剩余油量为
升,汽车每小时耗油
升.
(3)请直接写出两个变量之间的关系式(用t来表示Q).
23.一种豆子每千克售2元,豆子的总售价y(元)与所售豆子的质量x(千克)之间的关系如下表:
售出豆子质量x(千克)
0
0.5
1
1.5
2
2.5
3
5
总售价y(元)
0
1
2
3
4
5
6
10
(1)在这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当豆子售出5千克时,总售价是多少?
(3)按表中给出的关系,用一个式子把x与y之间的关系表示出来.
(4)当豆子售出20千克时,总售价是多少?
24.根据心理学家研究发现,学生对一个新概念的接受能力y与提出概念所用的时间x(分钟)之间有如表所示的关系:
提出概念所用时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
(1)上表中反映的两个变量之间的关系,哪个是自变量?哪个是因变量?
(2)根据表格中的数据,提出概念所用时间是多少分钟时,学生的接受能力最强?
(3)学生对一个新概念的接受能力从什么时间开始逐渐减弱?
25.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如表所示(每位乘客的公交票价是固定不变的).
x(人)
500
1000
1500
2000
2500
3000
…
y(元)
﹣3000
﹣2000
﹣1000
0
1000
2000
…
(1)在这个变化过程中,每月的乘车人数x与每月利润y分别是
变量和
变量;
(2)观察表中数据可知,每月乘客量达到
人以上时,该公交车才不会亏损;
(3)当每月乘车人数为4000人时,每月利润为多少元?
26.小亮想了解一根弹簧的长度是如何随所挂物体质量的变化而变化的,他把这根弹簧的上端固定,在其下端悬挂物体,下面是小亮测得的弹簧的长度y与所挂物体质量x的几组对应值.
所挂质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
30
32
34
36
38
40
(1)上表所反映的变化过程中的两个变量,
是自变量,
是因变量;
(2)直接写y与x的关系式;
(3)当弹簧长度为130cm(在弹簧承受范围内)时,求所挂重物的质量.
27.世界上大部分国家都使用摄氏温度(℃),但美国、英国等国家的天气预报仍然使用华氏温度(F).两种计量之间有如下对应:
摄氏温度(℃)
0
10
20
30
40
50
华氏温度(°F)
32
50
68
86
104
122
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)由上表可得:摄氏温度(℃)每提高10度,华氏温度(F)提高
度;
(3)摄氏温度100度时华氏温度为
度;
(4)华氏温度﹣4度时摄氏温度为
度;
(5)华氏温度的值与对应的摄氏温度的值有相等的可能吗?如果有,求出这个值.如果没有,请说明理由.
参考答案
1.解:由图表可以看出y与x符合一次函数关系,设y=kx+b(k≠0),
把x=90,y=90和x=100,y=80代入得,
,
解得:,
则y=﹣x+180,
当x=127时,y=﹣127+180=53.
故选:C.
2.解:设蓄水量为y,时间为t,
则可得y=50﹣2t,
A、放水时间是自变量,水池里的水量是因变量,故本选项符合题意;
B、蓄水池每分钟放水2m3,故本选项不合题意;
C、放水10分钟后,水池中水量为:y=50﹣2×10=30m3,故本选项不合题意;
D、蓄水池一共可以放水25分钟,故本选项不合题意;
故选:A.
3.解:当支撑物高度从10cm升高到20cm,下滑时间的减少0.24s,
从20cm升高到30cm时,下滑时间就减少0.2s,
从30cm升高到40cm时,下滑时间就减少0.15s,
从40cm升高到50cm时,下滑时间就减少0.1s,
因此,“高度每增加了10cm,时间就会减少0.24秒”是错误的,
故选:D.
4.解:A、自变量是温度,因变量是传播速度,故原题说法正确;
B、温度越高,传播速度越快,故原题说法正确;
C、当温度为10℃时,声音5s可以传播1680m,故原题说法错误;
D、温度每升高10℃,传播速度增加6m/s,故原题说法正确;
故选:C.
5.解:A.用电量每增加1千瓦?时,电费增加0.55元,故本选项正确;
B.若用电量为8千瓦?时,则应缴电费8×0.55=4.4元,故本选项正确;
C.若所缴电费为2.75元,则用电量为2.75÷0.55=5千瓦?时,故本选项错误;
D.所缴电费随用电量的增加而增加,故本选项正确;
故选:C.
6.解:A、氮肥施用量是自变量,土豆产量是因变量,原说法正确,故选项不符合题意;
B、当氮肥的施用量是101千克/公顷时,土豆的产量是32.29吨/公顷,原说法正确,故选项不符合题意;
C、如果不施氮肥,土豆的产量是15.18吨/公顷,原说法正确,故选项不符合题意;
D、氮肥施用量404千克/公顷比氮肥施用量336千克/公顷时的土豆的产量更低,原说法错误,故选项符合题意.
故选:D.
7.解:由图表可以看出y与x符合一次函数关系,设y=kx+b(k≠0),
把x=90,y=90和x=100,y=80代入得
,
解得:k=﹣1,b=180,
则y=﹣x+180,
当x=126时,y=﹣126+180=54.
故选:C.
8.解:根据表格数据可知:
因变量y(升)与自变量t(小时)之间的关系为:y=120﹣8t,
故答案为:y=120﹣8t.
9.解:观察表格数据可知:
y=20x,
当x=8时,y=160,
所以未铺设的管道长度为:1000﹣160=840(米).
故答案为:840.
10.解:根据题意得,y=0.6x+331,
当y=352时,352=0.6x+331,
解得x=35.
即当声音在空气中的传播速度为352米/秒,气温是35℃,
故答案为35.
11.解:当x=1时,y=1.2×1+0.1,
当x=2时,y=1.2×2+0.1,
当x=3时,y=1.2×3+0.1,
∴y=1.2x+0.1,
当x=10时,y=12.1,
故答案为:12.1.
12.解:由题可得,两个变量之间的关系为y=30+3(x﹣1),
∴当x=8时,y=30+3×7=51,
故答案为:51.
13.解:由表格数据得:老花镜的度数越高,镜片与光斑的距离越近;
且100×1=100,120×0.8=96≈100,200×0.5=100,250×0.4=100,300×0.3=90≈100,
100÷0.6≈160(度).
答:这幅老花镜的度数约为160度.
故答案为:160度.
14.解:从表中可以看出,烤鸭的质量每增加0.5千克,烤制的时间增加20分钟,由此可知烤制时间是烤鸭质量的一次函数.
设烤制时间为t分钟,烤鸭的质量为x千克,t与x的一次函数关系式为:t=kx+b,
,
解得,
所以t=40x+20.
当x=2.2千克时,t=40×2.2+20=108.
故答案为:108.
15.解:由图表可得出:
y=3x+0.1x=3.1x.
当x=10时,y=3.1×10=31,
故答案为:31.
16.解:当气温为15℃时,音速为340米/秒,而该人是看到发令枪的烟0.2秒后,听到了枪声.则由此可知,这个人距发令地点340×0.2=68米.
故答案为:68.
17.解:用时间t(s)表示高度h(m)的关系式为:h=5t2,
当t=2时,h=5×22=5×4=20.
所以果子开始落下时离地面的高度大约是20米.
故答案为:20.
18.解:设y=kx+b,
则把(1,55),(2,90)代入得:
,
解得:,
故y=35k+20,
则当y=230时,230=35x+20,
解得:x=6,
故答案为:6.
19.解:由题可得,y的值等于x的值的﹣3倍,
∴y=﹣3x,
故答案为:y=﹣3x.
20.解:从表格可以看到y随x的增大而增大;
20℃时,音速为343米/秒,343×0.2=68.6米,
这个人距离发令点68.6米;
故答案为增大,68.6;
21.解:由题意可得:气温为25℃,声音在空气中传播的速度为346米/秒,
∵驾驶员按响喇叭,4s后听到回声,
∴汽车距山崖346×4÷2=692(米),
故答案为:692.
22.解:(
1
)由题意可知,自变量为汽车行驶时间t,因变量为汽车油箱的剩余油量Q.
故答案为:汽车行驶时间t,汽车油箱的剩余油量Q.
(
2
)由表格可知,当行驶3小时的时候,汽车油箱的剩余油量为82升,且汽车每行驶一小时,耗油量为6升.
故答案为82,6.
(
3
)由表格可知,汽车一开始的油量为100升,每行驶一小时汽车耗油6升,则汽车油箱刺余油量和汽车行驶时间的关系为Q=100﹣6t.
故答案为Q=100﹣6t.
23.解:(1)表格中反映的是售出豆子质量x(千克)与总售价y(元)之间的关系,售出豆子的质量x(千克)是自变量,总售价y(元)是因变量;
(2)由图表可知,
售出5千克时,总售价为10元;
(3)设x与y之间的关系为:y=kx,
把x=1,y=2代入上式,
得k=2,
x与y之间的关系为y=2x;
(4)当豆子售出20千克时,
y=2×20=40(元),
当豆子售出20千克时,总售价是40元.
24.解:(1)表格中反映的是:提出概念所用时间与对概念的接受能力这两个变量,其中“提出概念所用时间”是自变量,“对概念的接受能力”为因变量;
(2)根据表格中的数据,提出概念所用时间是13分钟时,学生的接受能力最强达到59.9;
(3)学生对一个新概念的接受能力从第13分钟以后开始逐渐减弱.
25.解:(1)在这个变化过程中,每月的乘车人数是自变量,每月利润是因变量;
故答案为:每月的乘车人数,每月利润;
(2)根据表格可得:当每月乘客量达到2000人以上时,该公交车才不会亏损,
故答案为:2000;
(3)由表中的数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,利润为0元,故每月乘车人数为4000人时,每月的利润是4000元.
26.解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
故答案为:所挂物体质量,弹簧长度;
(2)由表格可得:当所挂物体重量为1千克时,弹簧长32厘米;当不挂重物时,弹簧长30厘米,
则y与x的关系式为:y=2x+30;
(3)当弹簧长度为130cm(在弹簧承受范围内)时,
130=2x+30,
解得x=50,
答:所挂重物的质量为50kg.
27.解:(1)反映摄氏温度(℃)和华氏温度(℉)之间的关系,摄氏温度是自变量,华氏温度是因变量;
(2)由上表可得:摄氏温度(℃)每提高10度,华氏温度(F)提高18度;
故答案为:18;
(3)设摄氏温度为x(℃)与华氏温度为y(℉)之间的函数关系式为y=kx+b,由题意,得
,解得,
即y=1.8x+32,
当x=100时,y=1.8×100+32=212.
摄氏温度100度时华氏温度为212度.
故答案为:212;
(4)由(3)得,当y=﹣4时,1.8x+32=﹣4,解得x=﹣20.
故华氏温度﹣4度时摄氏温度为﹣20度.
故答案为:﹣20;
(5)有;
当y=x时,x=1.8x+32,
解得:x=﹣40.
因此当华氏﹣40度时,摄氏也是﹣40度
1.在某一阶段,某商品的销售量与销售价之间存在如表关系:
销售价/元
90
100
110
120
130
140
销售量/件
90
80
70
60
50
40
设该商品的销售价为x元,销售量为y件,估计:当x=127时,y的值为( )
A.63
B.59
C.53
D.43
2.一个蓄水池有水50m3,打开放水闸门放水,水池里的水和放水时间的关系如表,下面说法不正确的是( )
放水时间(分)
1
2
3
4
…
水池中水量(m3)
48
46
44
42
…
A.水池里的水量是自变量,放水时间是因变量
B.每分钟放水2m3
C.放水10分钟后,水池里还有水30m3
D.放水25分钟,水池里的水全部放完
3.在实验课上,小亮利用同一块木板测得小车从不同高度(h)与下滑的时间(t)的关系如下表:
支撑物高h(cm)
10
20
30
40
50
…
下滑时间t(s)
3.25
3.01
2.81
2.66
2.56
…
以下结论错误的是( )
A.当h=40时,t约2.66秒
B.随高度增加,下滑时间越来越短
C.估计当h=80cm时,t一定小于2.56秒
D.高度每增加了10cm,时间就会减少0.24秒
4.已知声音在空气中的传播速度与空气的温度有关,在一定范围内,其关系如表所示,下列说法错误的是( )
温度/℃
﹣20
﹣10
0
10
20
30
传播速度/(m/s)
318
324
330
336
342
348
A.自变量是温度,因变量是传播速度
B.温度越高,传播速度越快
C.当温度为10℃时,声音5s可以传播1650m
D.温度每升高10℃,传播速度增加6m/s
5.某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦?时)
1
2
3
4
…
应缴电费(元)
0.55
1.10
1.65
2.20
…
A.用电量每增加1千瓦?时,电费增加0.55元
B.若用电量为8千瓦?时,则应缴电费4.4元
C.若应缴电费为2.75元,则用电量为6千瓦?时
D.应缴电费随用电量的增加而增加
6.研究表明,当每公顷钾肥和磷肥的施用量一定时,氮肥施用量与土豆的产量有如表所示的关系:
氮肥施用量/千克
0
34
67
101
135
202
259
336
404
471
土豆产量/吨
15.18
21.36
25.72
32.29
34.05
39.45
43.15
43.46
40.83
30.75
下列说法错误的是( )
A.氮肥施用量是自变量,土豆产量是因变量
B.当氮肥的施用量是101千克/公顷时,土豆的产量是32.29吨/公顷
C.如果不施氮肥,土豆的产量是15.18吨/公顷
D.氮肥施用量404千克/公顷比氮肥施用量336千克/公顷时的土豆的产量更高
7.在某一阶段,某商品的销售量与销售价之间存在如表关系:
销售价/元
90
100
110
120
130
140
销售量/件
90
80
70
60
50
40
设该商品的销售价为x元,销售量为y件,估计当x=126时,y的值为( )
A.64
B.57
C.54
D.47
8.某汽车生产厂家对其生产的一款汽车进行耗油量试验.在试验过程中,汽车一直匀速行驶,该汽车油箱中的余油量y(升)与汽车的行驶时间t(小时)之间的关系如表:
t(小时)
0
1
2
3
y(升)
120
112
104
96
则用关系式法表示因变量y(升)与自变量t(小时)之间的关系为:
.
9.农村“雨污分流”工程是“美丽乡村”战略的重要组成部分,我县某村要铺设一条全长为1000米的“雨污分流”管道,现在工程队铺设管道施工x天与铺设管道y米之间的关系用表格表示如下,则施工8天后,未铺设的管道长度为
米.
时间(x天)
1
2
3
4
5
…
管道长度(y米)
20
40
60
80
100
…
10.声音在空气中传播的速度y(m/s)(简称声速)与气温x(℃)的关系如下表所示:
气温x/℃
0
5
10
15
20
…
声速y/(m/s)
331
334
337
340
343
…
照此规律可以发现,当气温x为
℃时,声速y达到352m/s.
11.张大妈购进一批柚子,在集贸市场零售,已知卖出的柚子重量x(kg)与售价y(元)之间的关系如下表:
重量/kg
1
2
3
…
售价/元
1.2+0.1
2.4+0.1
3.6+0.1
…
根据表中数据可知,若卖出柚子10kg,则售价为
元.
12.某院观众的座位按下列方式设置,根据表格中两个变量之间的关系.
排数(x)
1
2
3
4
…
座位数(y)
30
33
36
39
…
则当x=8时,y=
.
13.小颖在课余时间找了几副度数不同的老花镜,让镜片正对太阳光,上下移动镜片,直到地上的光斑最小,此时他测量了镜片与光斑的距离,得到如表数据:
老花镜的度数x/度
100
120
200
250
300
镜片与光斑的距离y/m
1
0.8
0.5
0.4
0.3
如果按上述方法测得一副老花镜的镜片与光斑的距离为0.6m,则这副老花镜的度数约为
.
14.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是如表数据:
鸭的质量/千克
0.5
1
1.5
2
2.5
3
3.5
烤制时间/分钟
40
60
80
100
120
140
160
设鸭的质量为x千克,烤制时间为t,估计当x=2.2千克时,t的值为
.
15.某人购进一批苹果到市场上零售,已知卖出苹果数量x与售价y的关系如下表.
数量x(千克)
1
2
3
4
5
售价y(元)
3+0.1
6+0.2
9+0.3
12+0.4
15+0.5
则当卖出苹果数量为10千克时,售价y为
元.
16.声音在空气中传播的速度y(m/s)(简称音速)与气温x(℃)之间的关系如表:
气温x(℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
在气温为15℃的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,则由此可知,这个人距发令枪的地点有
m.
17.果子成熟后从树上落到地面,它落下的高度与经过的时间有如下的关系:
时间t(秒)
0.5
0.6
0.7
0.8
0.9
1
落下的高度h(米)
5×0.25
5×0.36
5×0.49
5×0.64
5×0.81
5×1
如果果子经过2秒落到地上,那么此果子开始落下时离地面的高度大约是
米.
18.地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间有如下关系:
x/km
1
2
3
4
y/℃
55
90
125
160
根据表格,估计地表以下岩层的温度为230℃时,岩层所处的深度为
km.
19.已知y与x的部分对应关系如下表:
x
…
﹣1
0
1
2
3
…
y
…
3
0
﹣3
﹣6
﹣9
…
则可得y与x的一个关系式
.
20.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下:
气温(x℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
从表中可知音速y随温度x的升高而
;在气温为20℃的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,则由此可知,这个人距发令地点
米.
21.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下.一辆汽车停在路边,其正前方有一座山崖,驾驶员按响喇叭,4s后听到回声,若当时的气温为25℃,则由此可知,汽车距山崖
米.
气温x(℃)
0
5
10
15
20
25
音速y(米/秒)
331
334
337
340
343
346
22.为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成如表:
汽车行驶时间t(小时)
0
1
2
3
…
油箱剩余油量Q(升)
100
94
88
82
…
(1)如表反映的两个变量中,自变量是
,因变量是
.
(2)根据表可知,汽车行驶3小时时,该车油箱的剩余油量为
升,汽车每小时耗油
升.
(3)请直接写出两个变量之间的关系式(用t来表示Q).
23.一种豆子每千克售2元,豆子的总售价y(元)与所售豆子的质量x(千克)之间的关系如下表:
售出豆子质量x(千克)
0
0.5
1
1.5
2
2.5
3
5
总售价y(元)
0
1
2
3
4
5
6
10
(1)在这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当豆子售出5千克时,总售价是多少?
(3)按表中给出的关系,用一个式子把x与y之间的关系表示出来.
(4)当豆子售出20千克时,总售价是多少?
24.根据心理学家研究发现,学生对一个新概念的接受能力y与提出概念所用的时间x(分钟)之间有如表所示的关系:
提出概念所用时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
(1)上表中反映的两个变量之间的关系,哪个是自变量?哪个是因变量?
(2)根据表格中的数据,提出概念所用时间是多少分钟时,学生的接受能力最强?
(3)学生对一个新概念的接受能力从什么时间开始逐渐减弱?
25.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如表所示(每位乘客的公交票价是固定不变的).
x(人)
500
1000
1500
2000
2500
3000
…
y(元)
﹣3000
﹣2000
﹣1000
0
1000
2000
…
(1)在这个变化过程中,每月的乘车人数x与每月利润y分别是
变量和
变量;
(2)观察表中数据可知,每月乘客量达到
人以上时,该公交车才不会亏损;
(3)当每月乘车人数为4000人时,每月利润为多少元?
26.小亮想了解一根弹簧的长度是如何随所挂物体质量的变化而变化的,他把这根弹簧的上端固定,在其下端悬挂物体,下面是小亮测得的弹簧的长度y与所挂物体质量x的几组对应值.
所挂质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
30
32
34
36
38
40
(1)上表所反映的变化过程中的两个变量,
是自变量,
是因变量;
(2)直接写y与x的关系式;
(3)当弹簧长度为130cm(在弹簧承受范围内)时,求所挂重物的质量.
27.世界上大部分国家都使用摄氏温度(℃),但美国、英国等国家的天气预报仍然使用华氏温度(F).两种计量之间有如下对应:
摄氏温度(℃)
0
10
20
30
40
50
华氏温度(°F)
32
50
68
86
104
122
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)由上表可得:摄氏温度(℃)每提高10度,华氏温度(F)提高
度;
(3)摄氏温度100度时华氏温度为
度;
(4)华氏温度﹣4度时摄氏温度为
度;
(5)华氏温度的值与对应的摄氏温度的值有相等的可能吗?如果有,求出这个值.如果没有,请说明理由.
参考答案
1.解:由图表可以看出y与x符合一次函数关系,设y=kx+b(k≠0),
把x=90,y=90和x=100,y=80代入得,
,
解得:,
则y=﹣x+180,
当x=127时,y=﹣127+180=53.
故选:C.
2.解:设蓄水量为y,时间为t,
则可得y=50﹣2t,
A、放水时间是自变量,水池里的水量是因变量,故本选项符合题意;
B、蓄水池每分钟放水2m3,故本选项不合题意;
C、放水10分钟后,水池中水量为:y=50﹣2×10=30m3,故本选项不合题意;
D、蓄水池一共可以放水25分钟,故本选项不合题意;
故选:A.
3.解:当支撑物高度从10cm升高到20cm,下滑时间的减少0.24s,
从20cm升高到30cm时,下滑时间就减少0.2s,
从30cm升高到40cm时,下滑时间就减少0.15s,
从40cm升高到50cm时,下滑时间就减少0.1s,
因此,“高度每增加了10cm,时间就会减少0.24秒”是错误的,
故选:D.
4.解:A、自变量是温度,因变量是传播速度,故原题说法正确;
B、温度越高,传播速度越快,故原题说法正确;
C、当温度为10℃时,声音5s可以传播1680m,故原题说法错误;
D、温度每升高10℃,传播速度增加6m/s,故原题说法正确;
故选:C.
5.解:A.用电量每增加1千瓦?时,电费增加0.55元,故本选项正确;
B.若用电量为8千瓦?时,则应缴电费8×0.55=4.4元,故本选项正确;
C.若所缴电费为2.75元,则用电量为2.75÷0.55=5千瓦?时,故本选项错误;
D.所缴电费随用电量的增加而增加,故本选项正确;
故选:C.
6.解:A、氮肥施用量是自变量,土豆产量是因变量,原说法正确,故选项不符合题意;
B、当氮肥的施用量是101千克/公顷时,土豆的产量是32.29吨/公顷,原说法正确,故选项不符合题意;
C、如果不施氮肥,土豆的产量是15.18吨/公顷,原说法正确,故选项不符合题意;
D、氮肥施用量404千克/公顷比氮肥施用量336千克/公顷时的土豆的产量更低,原说法错误,故选项符合题意.
故选:D.
7.解:由图表可以看出y与x符合一次函数关系,设y=kx+b(k≠0),
把x=90,y=90和x=100,y=80代入得
,
解得:k=﹣1,b=180,
则y=﹣x+180,
当x=126时,y=﹣126+180=54.
故选:C.
8.解:根据表格数据可知:
因变量y(升)与自变量t(小时)之间的关系为:y=120﹣8t,
故答案为:y=120﹣8t.
9.解:观察表格数据可知:
y=20x,
当x=8时,y=160,
所以未铺设的管道长度为:1000﹣160=840(米).
故答案为:840.
10.解:根据题意得,y=0.6x+331,
当y=352时,352=0.6x+331,
解得x=35.
即当声音在空气中的传播速度为352米/秒,气温是35℃,
故答案为35.
11.解:当x=1时,y=1.2×1+0.1,
当x=2时,y=1.2×2+0.1,
当x=3时,y=1.2×3+0.1,
∴y=1.2x+0.1,
当x=10时,y=12.1,
故答案为:12.1.
12.解:由题可得,两个变量之间的关系为y=30+3(x﹣1),
∴当x=8时,y=30+3×7=51,
故答案为:51.
13.解:由表格数据得:老花镜的度数越高,镜片与光斑的距离越近;
且100×1=100,120×0.8=96≈100,200×0.5=100,250×0.4=100,300×0.3=90≈100,
100÷0.6≈160(度).
答:这幅老花镜的度数约为160度.
故答案为:160度.
14.解:从表中可以看出,烤鸭的质量每增加0.5千克,烤制的时间增加20分钟,由此可知烤制时间是烤鸭质量的一次函数.
设烤制时间为t分钟,烤鸭的质量为x千克,t与x的一次函数关系式为:t=kx+b,
,
解得,
所以t=40x+20.
当x=2.2千克时,t=40×2.2+20=108.
故答案为:108.
15.解:由图表可得出:
y=3x+0.1x=3.1x.
当x=10时,y=3.1×10=31,
故答案为:31.
16.解:当气温为15℃时,音速为340米/秒,而该人是看到发令枪的烟0.2秒后,听到了枪声.则由此可知,这个人距发令地点340×0.2=68米.
故答案为:68.
17.解:用时间t(s)表示高度h(m)的关系式为:h=5t2,
当t=2时,h=5×22=5×4=20.
所以果子开始落下时离地面的高度大约是20米.
故答案为:20.
18.解:设y=kx+b,
则把(1,55),(2,90)代入得:
,
解得:,
故y=35k+20,
则当y=230时,230=35x+20,
解得:x=6,
故答案为:6.
19.解:由题可得,y的值等于x的值的﹣3倍,
∴y=﹣3x,
故答案为:y=﹣3x.
20.解:从表格可以看到y随x的增大而增大;
20℃时,音速为343米/秒,343×0.2=68.6米,
这个人距离发令点68.6米;
故答案为增大,68.6;
21.解:由题意可得:气温为25℃,声音在空气中传播的速度为346米/秒,
∵驾驶员按响喇叭,4s后听到回声,
∴汽车距山崖346×4÷2=692(米),
故答案为:692.
22.解:(
1
)由题意可知,自变量为汽车行驶时间t,因变量为汽车油箱的剩余油量Q.
故答案为:汽车行驶时间t,汽车油箱的剩余油量Q.
(
2
)由表格可知,当行驶3小时的时候,汽车油箱的剩余油量为82升,且汽车每行驶一小时,耗油量为6升.
故答案为82,6.
(
3
)由表格可知,汽车一开始的油量为100升,每行驶一小时汽车耗油6升,则汽车油箱刺余油量和汽车行驶时间的关系为Q=100﹣6t.
故答案为Q=100﹣6t.
23.解:(1)表格中反映的是售出豆子质量x(千克)与总售价y(元)之间的关系,售出豆子的质量x(千克)是自变量,总售价y(元)是因变量;
(2)由图表可知,
售出5千克时,总售价为10元;
(3)设x与y之间的关系为:y=kx,
把x=1,y=2代入上式,
得k=2,
x与y之间的关系为y=2x;
(4)当豆子售出20千克时,
y=2×20=40(元),
当豆子售出20千克时,总售价是40元.
24.解:(1)表格中反映的是:提出概念所用时间与对概念的接受能力这两个变量,其中“提出概念所用时间”是自变量,“对概念的接受能力”为因变量;
(2)根据表格中的数据,提出概念所用时间是13分钟时,学生的接受能力最强达到59.9;
(3)学生对一个新概念的接受能力从第13分钟以后开始逐渐减弱.
25.解:(1)在这个变化过程中,每月的乘车人数是自变量,每月利润是因变量;
故答案为:每月的乘车人数,每月利润;
(2)根据表格可得:当每月乘客量达到2000人以上时,该公交车才不会亏损,
故答案为:2000;
(3)由表中的数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,利润为0元,故每月乘车人数为4000人时,每月的利润是4000元.
26.解:(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
故答案为:所挂物体质量,弹簧长度;
(2)由表格可得:当所挂物体重量为1千克时,弹簧长32厘米;当不挂重物时,弹簧长30厘米,
则y与x的关系式为:y=2x+30;
(3)当弹簧长度为130cm(在弹簧承受范围内)时,
130=2x+30,
解得x=50,
答:所挂重物的质量为50kg.
27.解:(1)反映摄氏温度(℃)和华氏温度(℉)之间的关系,摄氏温度是自变量,华氏温度是因变量;
(2)由上表可得:摄氏温度(℃)每提高10度,华氏温度(F)提高18度;
故答案为:18;
(3)设摄氏温度为x(℃)与华氏温度为y(℉)之间的函数关系式为y=kx+b,由题意,得
,解得,
即y=1.8x+32,
当x=100时,y=1.8×100+32=212.
摄氏温度100度时华氏温度为212度.
故答案为:212;
(4)由(3)得,当y=﹣4时,1.8x+32=﹣4,解得x=﹣20.
故华氏温度﹣4度时摄氏温度为﹣20度.
故答案为:﹣20;
(5)有;
当y=x时,x=1.8x+32,
解得:x=﹣40.
因此当华氏﹣40度时,摄氏也是﹣40度
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
