18.1.2平行四边形判定第4课时 三角形的中位线-2020-2021学年人教版八年级数学下册导学案(Word版含详解)
文档属性
| 名称 | 18.1.2平行四边形判定第4课时 三角形的中位线-2020-2021学年人教版八年级数学下册导学案(Word版含详解) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 14:54:41 | ||
图片预览

文档简介
18.1.2
平行四边形的判定
第4课时
三角形的中位线
学习目标:
1.熟练口述三角形中位线的概念,三角形的中位线定理.
2.能利用三角形的中位线定理解决有关证明和计算问题.
重点:能利用三角形的中位线定理解决有关证明和计算问题.
一、课前检测
四边形OABC在平面直角坐标系中,已知点A(3,0),C(2,2),若要使四边形OABC为平行四边形,则点B的坐标为_________.
二、温故知新
1.平行四边形的性质和判定有哪些?
边:①AB∥CD,AD____BC
②AB=CD,AD____BC
平行四边形ABCD
③AB∥CD,AB_____CD
角:∠BAD____∠BCD,∠ABC____∠ADC
对角线:AO____CO,DO____BO
三、预习导航(预习教材47-49页,标出你认为重要的关键词)
1.什么叫做三角形的中位线?一个三角形有几条中位线?
2.三角形的中位线有何性质?结合下图用几何语言表示这条性质.
4、自学自测
如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长.
五、我的疑惑(反思)
1、要点探究
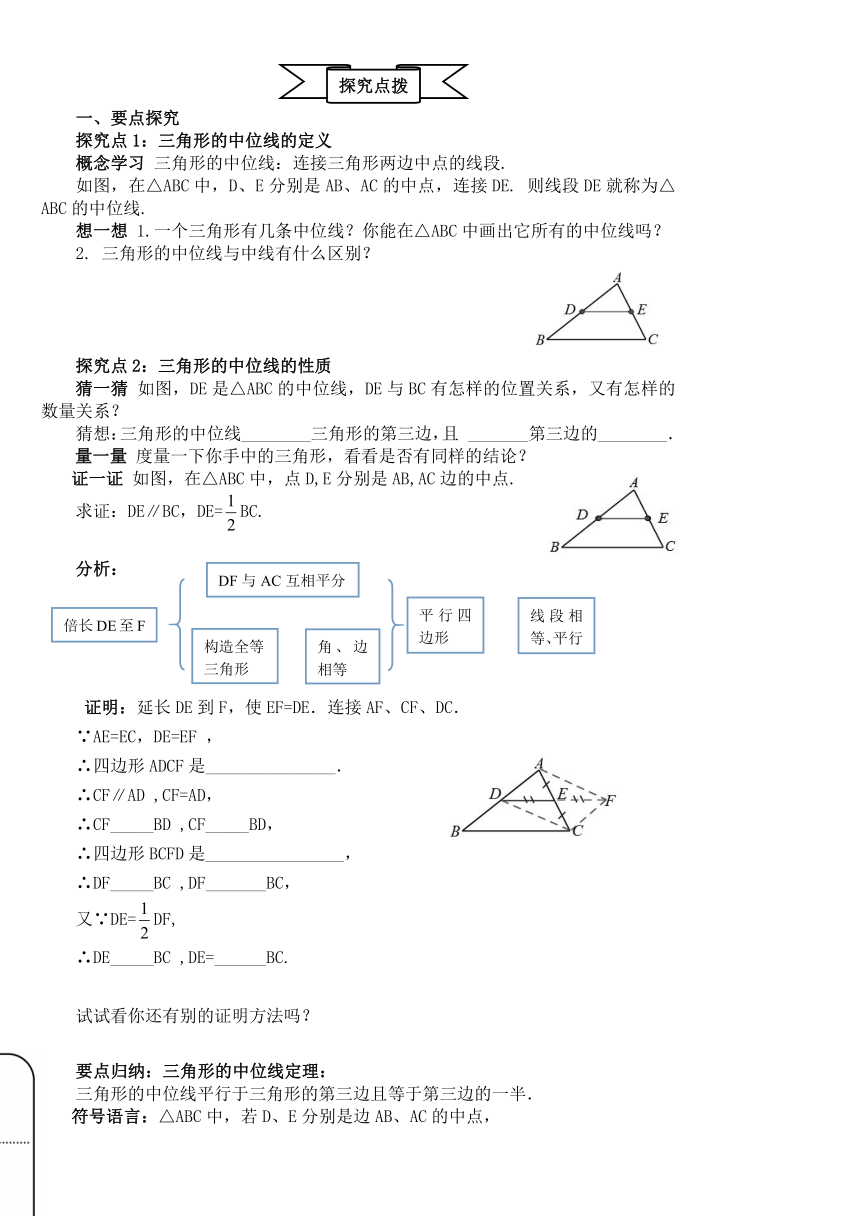
探究点1:三角形的中位线的定义
概念学习
三角形的中位线:连接三角形两边中点的线段.
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE.
则线段DE就称为△ABC的中位线.
想一想
1.一个三角形有几条中位线?你能在△ABC中画出它所有的中位线吗?
2.
三角形的中位线与中线有什么区别?
探究点2:三角形的中位线的性质
猜一猜
如图,DE是△ABC的中位线,DE与BC有怎样的位置关系,又有怎样的数量关系?
猜想:三角形的中位线________三角形的第三边,且
_______第三边的________.
量一量
度量一下你手中的三角形,看看是否有同样的结论?
证一证
如图,在△ABC中,点D,E分别是AB,AC边的中点.
求证:DE∥BC,DE=BC.
分析:
证明:延长DE到F,使EF=DE.连接AF、CF、DC.
∵AE=EC,DE=EF
,
∴四边形ADCF是_______________.
∴CF∥AD
,CF=AD,
∴CF_____BD
,CF_____BD,
∴四边形BCFD是________________,
∴DF_____BC
,DF_______BC,
又∵DE=DF,
∴DE_____BC
,DE=______BC.
试试看你还有别的证明方法吗?
要点归纳:三角形的中位线定理:
三角形的中位线平行于三角形的第三边且等于第三边的一半.
符号语言:△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE=BC.
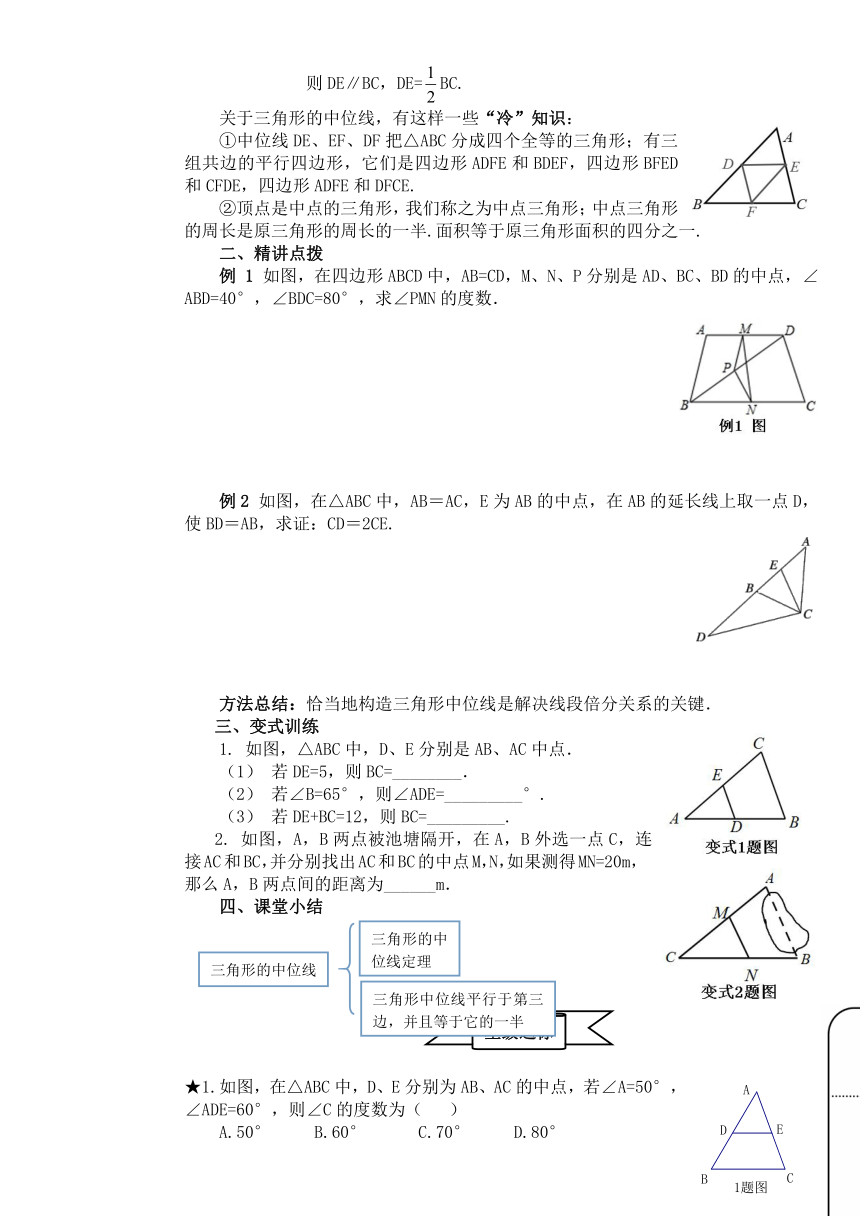
关于三角形的中位线,有这样一些“冷”知识:
①中位线DE、EF、DF把△ABC分成四个全等的三角形;有三组共边的平行四边形,它们是四边形ADFE和BDEF,四边形BFED和CFDE,四边形ADFE和DFCE.
②顶点是中点的三角形,我们称之为中点三角形;中点三角形的周长是原三角形的周长的一半.面积等于原三角形面积的四分之一.
二、精讲点拨
例
1
如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=40°,∠BDC=80°,求∠PMN的度数.
例2
如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.
方法总结:恰当地构造三角形中位线是解决线段倍分关系的关键.
三、变式训练
1.
如图,△ABC中,D、E分别是AB、AC中点.
(1)
若DE=5,则BC=________.
(2)
若∠B=65°,则∠ADE=_________°.
(3)
若DE+BC=12,则BC=_________.
2.
如图,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,并分别找出AC和BC的中点M,N,如果测得MN=20m,那么A,B两点间的距离为______m.
四、课堂小结
★1.如图,在△ABC中,D、E分别为AB、AC的中点,若∠A=50°,∠ADE=60°,则∠C的度数为(
)
A.50°
B.60°
C.70°
D.80°
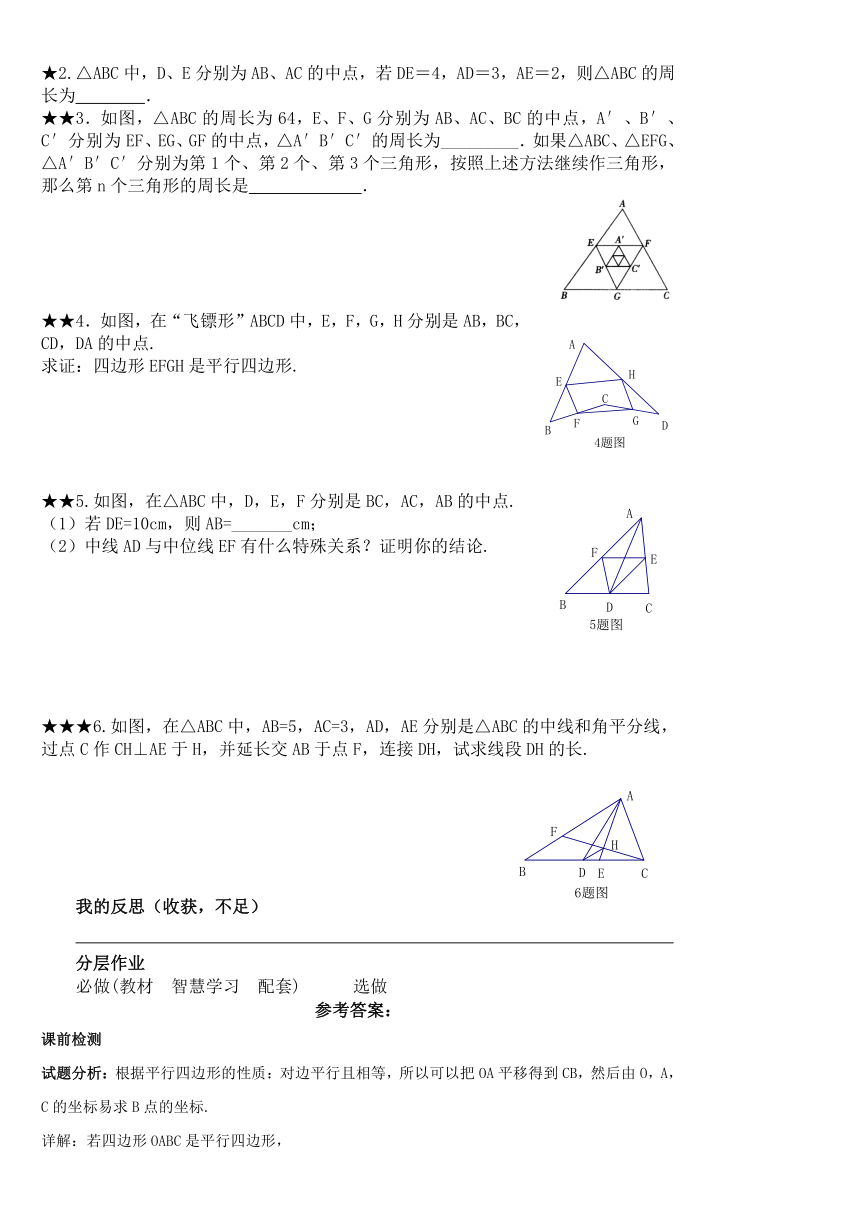
★2.△ABC中,D、E分别为AB、AC的中点,若DE=4,AD=3,AE=2,则△ABC的周长为
.
★★3.如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是
.
★★4.如图,在“飞镖形”ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
★★5.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.
(1)若DE=10cm,则AB=_______cm;
(2)中线AD与中位线EF有什么特殊关系?证明你的结论.
★★★6.如图,在△ABC中,AB=5,AC=3,AD,AE分别是△ABC的中线和角平分线,过点C作CH⊥AE于H,并延长交AB于点F,连接DH,试求线段DH的长.
我的反思(收获,不足)
分层作业
必做(教材
智慧学习
配套)
选做
参考答案:
课前检测
试题分析:根据平行四边形的性质:对边平行且相等,所以可以把OA平移得到CB,然后由O,A,C的坐标易求B点的坐标.
详解:若四边形OABC是平行四边形,
∴OA=CB,OA∥CB,
∵O(0,0),A(3,0),
∴OA=CB=3.
又∵C(2,2),
∴B(5,2)
故答案应填(5,2).
自学自测
试题分析:本题考查了三角形中位线定理,首先根据条件D、E分别是AC、BC的中点可得DE∥AB,∠2=∠3,再根据角平分线的定义推知∠1=∠3,则∠1=∠2,所以由等角对等边可得到DA=DF=AC.即可得出结论.
详解:如图,∵D、E分别为AC、BC的中点,
∴DE是△ABC的中位线.
∴DE∥AB,∴∠2=∠3.
又∵AF平分∠CAB,∴∠1=∠3.
∴∠1=∠2,∴AD=DF=3.
∴AC=2AD=6.
精讲点拨
例
1
试题分析:本题考查了三角形中位线定理,等腰三角形的性质.由M、N、P分别是AD、BC、BD的中点,得PN,PM分别是△CDB与△DAB的中位线,利用中位线的性质结合AB=CD,可得△PMN是等腰三角形.再利用三角形的内角和公式可求得结果.
详解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线.
∴PM=AB,PN=DC,PM∥AB,PN∥DC.
∵AB=CD,∴PM=PN,∴△PMN是等腰三角形.
∵PM∥AB,PN∥DC,∴∠MPD=∠ABD=40°,∠BPN=∠BDC=80°,
∴∠NPD=180°-∠BPN=100°.
∴∠MPN=∠MPD+∠NPD=40°+100°=140°.
∵PM=PN,∴∠PMN=∠PNM==20°.
例2
试题分析:本题考查了三角形的中位线的性质,全等三角形的判定与性质,作辅助线构造出全等三角形并利用三角形的中位线定理是解题的关键.取AC的中点F,连接BF,判断出BF是△ACD的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半可得CD=2BF,再求出AE=AF,然后利用“边角边”证明△ABF和△ACE全等,根据全等三角形对应边相等可得CE=BF,从而得证.
【详解】
证明:如图,取AC的中点F,连接BF.
∵BD=BA,
∴BF是△ACD的中位线,
∴CD=2BF,
又∵E是AB中点,AB=AC,
∴AE=AF=AB,
在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴CE=BF,
∴CD=2CE.
变式训练
1.试题分析:本题考查了三角形的中位线定理,点D、E分别是AB、AC的中点,所以DE是△ABC的中位线,有DE∥BC,DE=BC,据此结合已知条件可求得结果.
详解:在△ABC中,
∵点D、E分别是AB、AC的中点,∴DE∥BC,DE=BC.
∵DE=5,∴BC=10.
∵DE∥BC,∴∠ADE=∠B=65°.
∵DE=BC,DE+BC=12,∴BC=8.
故答案分别为10,
65°,8.
2.试题分析:根据三角形中位线定理:三角形的中位线平行第三边,且等于第三边的一半,那么第三边应等于中位线长的2倍.
详解:∵M,N分别是AC,BC的中点,∴MN是△ABC的中位线,
∴MN=AB,∴AB=2MN=2×20=40(m).
故答案应填40.
星级达标:
1.
试题分析:由三角形的中位线定理及三角形的内角和定理计算可确定结论.
详解:由题意得,∠AED=180°﹣∠A﹣∠ADE=70°,
∵点D,E分别是AB,AC的中点,∴DE是△ABC的中位线.
∴DE∥BC.∴∠C=∠AED=70°.
故选C.
2.试题分析:三角形的中位线平行第三边,且等于第三边的一半,那么第三边应等于中位线长的2倍,本题中DE是△ABC的中位线,可得BC=2DE,AB=2AD,AC=2AE,计算可得△ABC的周长.
详解:∵点D,E分别是△ABC的边AB,AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=2×4=8,
且AB=2AD=2×3=6,AC=2AE=2×2=4,
∴AB+AC+BC=18,
即△ABC的周长为18,
故答案为18.
3.试题分析:根据E、F、G分别为AB、AC、BC的中点,可以判断EF、FG、EG为三角形中位线,利用中位线定理求出EF、FG、EG与BC、AB、CA的长度关系,即可求得△EFG的周长是△ABC周长的一半,△A′B′C′的周长是△EFG的周长的一半,以此类推,可以求得第n个三角形的周长.
详解:∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半.
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16.
以此类推,第n个小三角形的周长是第一个三角形周长的64×.
故答案是:.
4.试题分析:连接AC,根据三角形的中位线定理求出EH=BD,HG=AC,EH∥BD,HG∥AC,FG∥BD,EF∥AC,推出平行四边形EFGH即可.
【详解】
证明:连接AC.
∵E、F、G、H分别是AB、BC、CD、AD的中点.
∴EF、GH分别是△ABC、△ACD的中位线.
∴EF∥AC,EF=AC,GH∥AC,GH=AC,
∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形.
5.试题分析:(1)根据三角形中位线定理计算即可;
(2)根据平行四边形的判定和性质解答即可.
详解:(1)∵D,E分别是BC、AC边的中点,∴AB=2DE=20cm.故答案为:20;
(2)AD与EF互相平分
.理由如下:
∵
D、E分别是BC
、AC边的中点,∴
DE∥AB,
同理:EF∥BC,∴四边形AEDF是平行四边形,∴AD、EF互相平分.
6.试题分析:本题考查了等腰三角形的判定以及三角形的中位线定理,正确证明HF=CH是关键.首先证明△ACF是等腰三角形,则AF=AC=3,HF=CH,则DH是△BCF的中位线,利用三角形的中位线定理即可求解.
详解∵AE为△ABC的角平分线,CH⊥AE,
∴∠CAH=∠FAH,∠AHC=∠AHF=90°.
又∵AH=AH,
∴△ACH≌△AFH(ASA).
∴AF=AC=3,HF=CH,
∵AD为△ABC的中线,BD=CD,
∴DH是△BCF的中位线,
∴DH=BF,
∵AB=5,
∴BF=AB-AF=5-3=2.∴DH=1.
自主研习
性
质
判
定
探究点拨
DF与AC互相平分
线段相等、平行
平行四边形
倍长DE至F
角、边相等
构造全等
三角形
三角形的中位线定理
三角形的中位线
三角形中位线平行于第三边,并且等于它的一半
星级达标
平行四边形的判定
第4课时
三角形的中位线
学习目标:
1.熟练口述三角形中位线的概念,三角形的中位线定理.
2.能利用三角形的中位线定理解决有关证明和计算问题.
重点:能利用三角形的中位线定理解决有关证明和计算问题.
一、课前检测
四边形OABC在平面直角坐标系中,已知点A(3,0),C(2,2),若要使四边形OABC为平行四边形,则点B的坐标为_________.
二、温故知新
1.平行四边形的性质和判定有哪些?
边:①AB∥CD,AD____BC
②AB=CD,AD____BC
平行四边形ABCD
③AB∥CD,AB_____CD
角:∠BAD____∠BCD,∠ABC____∠ADC
对角线:AO____CO,DO____BO
三、预习导航(预习教材47-49页,标出你认为重要的关键词)
1.什么叫做三角形的中位线?一个三角形有几条中位线?
2.三角形的中位线有何性质?结合下图用几何语言表示这条性质.
4、自学自测
如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长.
五、我的疑惑(反思)
1、要点探究
探究点1:三角形的中位线的定义
概念学习
三角形的中位线:连接三角形两边中点的线段.
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE.
则线段DE就称为△ABC的中位线.
想一想
1.一个三角形有几条中位线?你能在△ABC中画出它所有的中位线吗?
2.
三角形的中位线与中线有什么区别?
探究点2:三角形的中位线的性质
猜一猜
如图,DE是△ABC的中位线,DE与BC有怎样的位置关系,又有怎样的数量关系?
猜想:三角形的中位线________三角形的第三边,且
_______第三边的________.
量一量
度量一下你手中的三角形,看看是否有同样的结论?
证一证
如图,在△ABC中,点D,E分别是AB,AC边的中点.
求证:DE∥BC,DE=BC.
分析:
证明:延长DE到F,使EF=DE.连接AF、CF、DC.
∵AE=EC,DE=EF
,
∴四边形ADCF是_______________.
∴CF∥AD
,CF=AD,
∴CF_____BD
,CF_____BD,
∴四边形BCFD是________________,
∴DF_____BC
,DF_______BC,
又∵DE=DF,
∴DE_____BC
,DE=______BC.
试试看你还有别的证明方法吗?
要点归纳:三角形的中位线定理:
三角形的中位线平行于三角形的第三边且等于第三边的一半.
符号语言:△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE=BC.
关于三角形的中位线,有这样一些“冷”知识:
①中位线DE、EF、DF把△ABC分成四个全等的三角形;有三组共边的平行四边形,它们是四边形ADFE和BDEF,四边形BFED和CFDE,四边形ADFE和DFCE.
②顶点是中点的三角形,我们称之为中点三角形;中点三角形的周长是原三角形的周长的一半.面积等于原三角形面积的四分之一.
二、精讲点拨
例
1
如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=40°,∠BDC=80°,求∠PMN的度数.
例2
如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.
方法总结:恰当地构造三角形中位线是解决线段倍分关系的关键.
三、变式训练
1.
如图,△ABC中,D、E分别是AB、AC中点.
(1)
若DE=5,则BC=________.
(2)
若∠B=65°,则∠ADE=_________°.
(3)
若DE+BC=12,则BC=_________.
2.
如图,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,并分别找出AC和BC的中点M,N,如果测得MN=20m,那么A,B两点间的距离为______m.
四、课堂小结
★1.如图,在△ABC中,D、E分别为AB、AC的中点,若∠A=50°,∠ADE=60°,则∠C的度数为(
)
A.50°
B.60°
C.70°
D.80°
★2.△ABC中,D、E分别为AB、AC的中点,若DE=4,AD=3,AE=2,则△ABC的周长为
.
★★3.如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是
.
★★4.如图,在“飞镖形”ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
★★5.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.
(1)若DE=10cm,则AB=_______cm;
(2)中线AD与中位线EF有什么特殊关系?证明你的结论.
★★★6.如图,在△ABC中,AB=5,AC=3,AD,AE分别是△ABC的中线和角平分线,过点C作CH⊥AE于H,并延长交AB于点F,连接DH,试求线段DH的长.
我的反思(收获,不足)
分层作业
必做(教材
智慧学习
配套)
选做
参考答案:
课前检测
试题分析:根据平行四边形的性质:对边平行且相等,所以可以把OA平移得到CB,然后由O,A,C的坐标易求B点的坐标.
详解:若四边形OABC是平行四边形,
∴OA=CB,OA∥CB,
∵O(0,0),A(3,0),
∴OA=CB=3.
又∵C(2,2),
∴B(5,2)
故答案应填(5,2).
自学自测
试题分析:本题考查了三角形中位线定理,首先根据条件D、E分别是AC、BC的中点可得DE∥AB,∠2=∠3,再根据角平分线的定义推知∠1=∠3,则∠1=∠2,所以由等角对等边可得到DA=DF=AC.即可得出结论.
详解:如图,∵D、E分别为AC、BC的中点,
∴DE是△ABC的中位线.
∴DE∥AB,∴∠2=∠3.
又∵AF平分∠CAB,∴∠1=∠3.
∴∠1=∠2,∴AD=DF=3.
∴AC=2AD=6.
精讲点拨
例
1
试题分析:本题考查了三角形中位线定理,等腰三角形的性质.由M、N、P分别是AD、BC、BD的中点,得PN,PM分别是△CDB与△DAB的中位线,利用中位线的性质结合AB=CD,可得△PMN是等腰三角形.再利用三角形的内角和公式可求得结果.
详解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线.
∴PM=AB,PN=DC,PM∥AB,PN∥DC.
∵AB=CD,∴PM=PN,∴△PMN是等腰三角形.
∵PM∥AB,PN∥DC,∴∠MPD=∠ABD=40°,∠BPN=∠BDC=80°,
∴∠NPD=180°-∠BPN=100°.
∴∠MPN=∠MPD+∠NPD=40°+100°=140°.
∵PM=PN,∴∠PMN=∠PNM==20°.
例2
试题分析:本题考查了三角形的中位线的性质,全等三角形的判定与性质,作辅助线构造出全等三角形并利用三角形的中位线定理是解题的关键.取AC的中点F,连接BF,判断出BF是△ACD的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半可得CD=2BF,再求出AE=AF,然后利用“边角边”证明△ABF和△ACE全等,根据全等三角形对应边相等可得CE=BF,从而得证.
【详解】
证明:如图,取AC的中点F,连接BF.
∵BD=BA,
∴BF是△ACD的中位线,
∴CD=2BF,
又∵E是AB中点,AB=AC,
∴AE=AF=AB,
在△ABF和△ACE中,
,
∴△ABF≌△ACE(SAS),
∴CE=BF,
∴CD=2CE.
变式训练
1.试题分析:本题考查了三角形的中位线定理,点D、E分别是AB、AC的中点,所以DE是△ABC的中位线,有DE∥BC,DE=BC,据此结合已知条件可求得结果.
详解:在△ABC中,
∵点D、E分别是AB、AC的中点,∴DE∥BC,DE=BC.
∵DE=5,∴BC=10.
∵DE∥BC,∴∠ADE=∠B=65°.
∵DE=BC,DE+BC=12,∴BC=8.
故答案分别为10,
65°,8.
2.试题分析:根据三角形中位线定理:三角形的中位线平行第三边,且等于第三边的一半,那么第三边应等于中位线长的2倍.
详解:∵M,N分别是AC,BC的中点,∴MN是△ABC的中位线,
∴MN=AB,∴AB=2MN=2×20=40(m).
故答案应填40.
星级达标:
1.
试题分析:由三角形的中位线定理及三角形的内角和定理计算可确定结论.
详解:由题意得,∠AED=180°﹣∠A﹣∠ADE=70°,
∵点D,E分别是AB,AC的中点,∴DE是△ABC的中位线.
∴DE∥BC.∴∠C=∠AED=70°.
故选C.
2.试题分析:三角形的中位线平行第三边,且等于第三边的一半,那么第三边应等于中位线长的2倍,本题中DE是△ABC的中位线,可得BC=2DE,AB=2AD,AC=2AE,计算可得△ABC的周长.
详解:∵点D,E分别是△ABC的边AB,AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=2×4=8,
且AB=2AD=2×3=6,AC=2AE=2×2=4,
∴AB+AC+BC=18,
即△ABC的周长为18,
故答案为18.
3.试题分析:根据E、F、G分别为AB、AC、BC的中点,可以判断EF、FG、EG为三角形中位线,利用中位线定理求出EF、FG、EG与BC、AB、CA的长度关系,即可求得△EFG的周长是△ABC周长的一半,△A′B′C′的周长是△EFG的周长的一半,以此类推,可以求得第n个三角形的周长.
详解:∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半.
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16.
以此类推,第n个小三角形的周长是第一个三角形周长的64×.
故答案是:.
4.试题分析:连接AC,根据三角形的中位线定理求出EH=BD,HG=AC,EH∥BD,HG∥AC,FG∥BD,EF∥AC,推出平行四边形EFGH即可.
【详解】
证明:连接AC.
∵E、F、G、H分别是AB、BC、CD、AD的中点.
∴EF、GH分别是△ABC、△ACD的中位线.
∴EF∥AC,EF=AC,GH∥AC,GH=AC,
∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形.
5.试题分析:(1)根据三角形中位线定理计算即可;
(2)根据平行四边形的判定和性质解答即可.
详解:(1)∵D,E分别是BC、AC边的中点,∴AB=2DE=20cm.故答案为:20;
(2)AD与EF互相平分
.理由如下:
∵
D、E分别是BC
、AC边的中点,∴
DE∥AB,
同理:EF∥BC,∴四边形AEDF是平行四边形,∴AD、EF互相平分.
6.试题分析:本题考查了等腰三角形的判定以及三角形的中位线定理,正确证明HF=CH是关键.首先证明△ACF是等腰三角形,则AF=AC=3,HF=CH,则DH是△BCF的中位线,利用三角形的中位线定理即可求解.
详解∵AE为△ABC的角平分线,CH⊥AE,
∴∠CAH=∠FAH,∠AHC=∠AHF=90°.
又∵AH=AH,
∴△ACH≌△AFH(ASA).
∴AF=AC=3,HF=CH,
∵AD为△ABC的中线,BD=CD,
∴DH是△BCF的中位线,
∴DH=BF,
∵AB=5,
∴BF=AB-AF=5-3=2.∴DH=1.
自主研习
性
质
判
定
探究点拨
DF与AC互相平分
线段相等、平行
平行四边形
倍长DE至F
角、边相等
构造全等
三角形
三角形的中位线定理
三角形的中位线
三角形中位线平行于第三边,并且等于它的一半
星级达标
