九年级教学设计相似三角形学案3
文档属性
| 名称 | 九年级教学设计相似三角形学案3 |  | |
| 格式 | zip | ||
| 文件大小 | 45.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-23 19:21:49 | ||
图片预览

文档简介
九年级教学设计 ( http: / / www.21cnjy.com / " \l "m=0&t=1&c=fks_087070092087087069086082086095085084087074092085086074086" \o "欢迎登陆21世纪教育网 )相似三角形学案3
课 题 相似三角形的判定3 课 型 新授课
单 位 主备人
学习目标 掌握判定两个三角形相似的方法:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
学习重、难点 两个三角形相似的判定方法及其应用
学法指导 通过动手操作,类比归纳,合作交流得到解决问题的方法。
学 习 过 程 教师个性修订
新课引入:复习两个三角形相似的判定方法1﹑2与全等三角形判定方法(SSS﹑SAS)的区别与联系:
提出问题: 观察两副三角尺,其中同样角度(300与600,或450与450)的两个三角尺大小可能不同,但它们看起来是相似的。思考:如果两个三角形有两组角对应相等,它们一定相似吗? 探究问题:作 ABC与 A1B1C1,使得∠A=∠A1,∠B=∠B1,这时它们的第三角满足∠C=∠C1吗?分别度量这两个三角形的边长,计算 ﹑ ﹑ ,你有什么发现?(独立操作并判断) 分别改变这两个三角形边的大小,而不改变它们的角的大小,再试一试,是否有同样的结论?(利用刻度尺和量角器,小组合作再作出具体判断。)
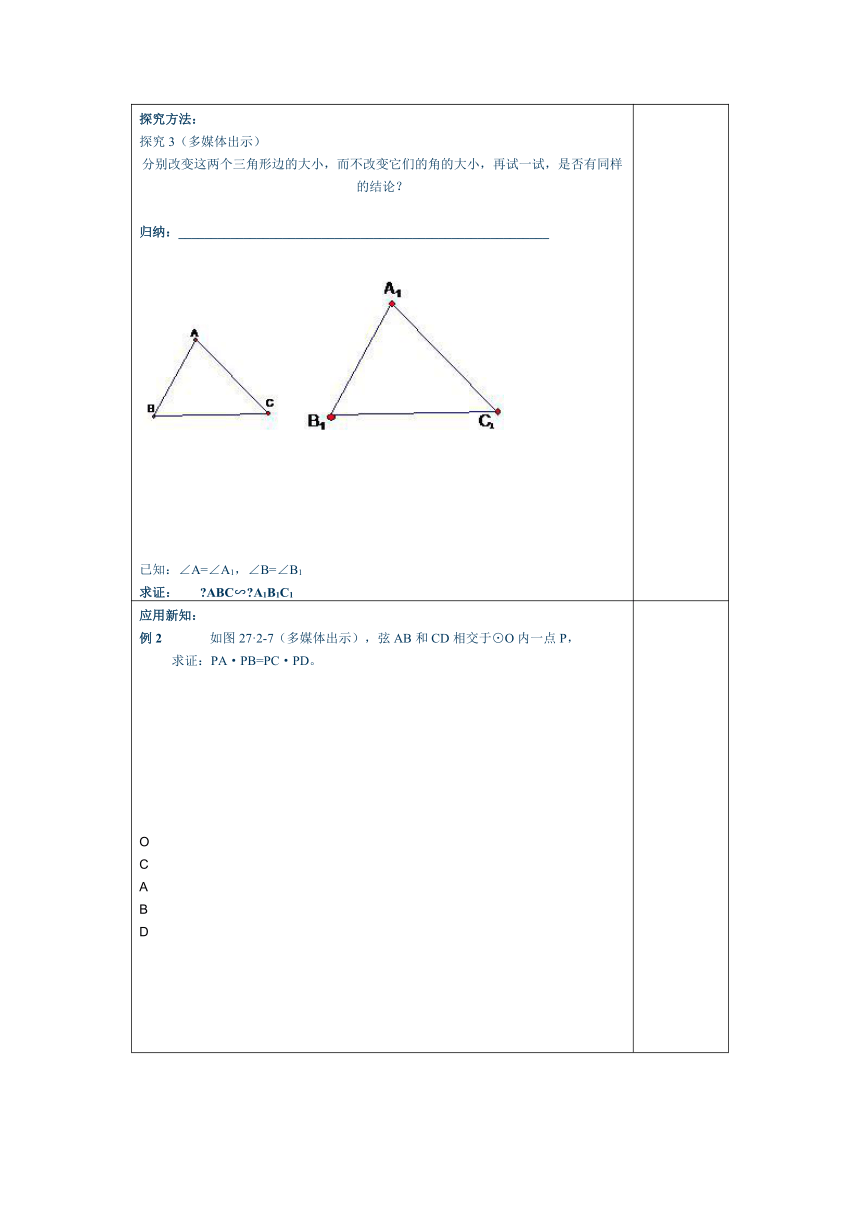
探究方法:探究3(多媒体出示)分别改变这两个三角形边的大小,而不改变它们的角的大小,再试一试,是否有同样的结论? 归纳:_________________________________________________________ 已知:∠A=∠A1,∠B=∠B1求证: ABC∽ A1B1C1
应用新知:例2 如图27·2-7(多媒体出示),弦AB和CD相交于⊙O内一点P,求证:PA·PB=PC·PD。 OCABD 小试牛刀如图、D、E分别是AB,AC上的点,(1)∠AED=∠B;; ,能够判断 ADE∽ ACB相似的是 ( http: / / img.bimg. / photo / 5OBCFFQWMCdAEC6-sXLzKw== / 3443283390103494178.jpg" \t "_blank )( )A、(1)(2) B、(1)(3)C、(1)(2)(3)D(1)达标检测必做题1、 如图,任意 ABC三边的高AD,BE,CF相交与点H,图中和Rt BDH相似的三角形(不包括 BDH本身)有( )A 5个 B 4个 C 3个 D 2个2、已知 ABC,P是边AC上的一点,连接BP,以下条件中不能判定 ABP∽ ACB的是( )A、∠ABP=∠C B∠APB=∠ABC 选做题如图、等边 ABC,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F,(1)试说明 ABD=∽ BCE(2) AEF与 ABE相似吗/ 说说你的理由。(3)BD2= AD·DF吗?请说明理由。
课 题 相似三角形的判定3 课 型 新授课
单 位 主备人
学习目标 掌握判定两个三角形相似的方法:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
学习重、难点 两个三角形相似的判定方法及其应用
学法指导 通过动手操作,类比归纳,合作交流得到解决问题的方法。
学 习 过 程 教师个性修订
新课引入:复习两个三角形相似的判定方法1﹑2与全等三角形判定方法(SSS﹑SAS)的区别与联系:
提出问题: 观察两副三角尺,其中同样角度(300与600,或450与450)的两个三角尺大小可能不同,但它们看起来是相似的。思考:如果两个三角形有两组角对应相等,它们一定相似吗? 探究问题:作 ABC与 A1B1C1,使得∠A=∠A1,∠B=∠B1,这时它们的第三角满足∠C=∠C1吗?分别度量这两个三角形的边长,计算 ﹑ ﹑ ,你有什么发现?(独立操作并判断) 分别改变这两个三角形边的大小,而不改变它们的角的大小,再试一试,是否有同样的结论?(利用刻度尺和量角器,小组合作再作出具体判断。)
探究方法:探究3(多媒体出示)分别改变这两个三角形边的大小,而不改变它们的角的大小,再试一试,是否有同样的结论? 归纳:_________________________________________________________ 已知:∠A=∠A1,∠B=∠B1求证: ABC∽ A1B1C1
应用新知:例2 如图27·2-7(多媒体出示),弦AB和CD相交于⊙O内一点P,求证:PA·PB=PC·PD。 OCABD 小试牛刀如图、D、E分别是AB,AC上的点,(1)∠AED=∠B;; ,能够判断 ADE∽ ACB相似的是 ( http: / / img.bimg. / photo / 5OBCFFQWMCdAEC6-sXLzKw== / 3443283390103494178.jpg" \t "_blank )( )A、(1)(2) B、(1)(3)C、(1)(2)(3)D(1)达标检测必做题1、 如图,任意 ABC三边的高AD,BE,CF相交与点H,图中和Rt BDH相似的三角形(不包括 BDH本身)有( )A 5个 B 4个 C 3个 D 2个2、已知 ABC,P是边AC上的一点,连接BP,以下条件中不能判定 ABP∽ ACB的是( )A、∠ABP=∠C B∠APB=∠ABC 选做题如图、等边 ABC,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F,(1)试说明 ABD=∽ BCE(2) AEF与 ABE相似吗/ 说说你的理由。(3)BD2= AD·DF吗?请说明理由。
