2020-2021学年八年级数学苏科版下册第11章 反比例函数与几何综合题专题练习(1)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级数学苏科版下册第11章 反比例函数与几何综合题专题练习(1)(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 728.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 19:10:51 | ||
图片预览




文档简介
2021八年级反比例函数与几何综合题专题练习(1)
1.如图,平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=(k≠0)的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1>y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若AD=3CD,求点C的坐标.
2.如图,已知直线与双曲线交于、两点,点横坐标为4.
(1)求值;
(2)直接写出关于的不等式的解集;
(3)若双曲线上有一点的纵坐标为8,求的面积;
(4)若在轴上有点,轴上有点,且点、、、四点恰好构成平行四边形,直接写出点、的坐标.
3.如图,函数与函数的图像相交于点.点在函数的图像上,过点作轴,与轴相交于点,且.
(1)求的值;
(2)求直线的函数表达式.
4.如图,直线都与双曲线
交于点,这两条直线分别与
x轴交于B,C两点.
(1)试确定k的值;
(2)直接写出当时,不等式的解集;
(3)若点P在x轴上,连接,把的面积分成两部分,求此时点
P的坐标.
5.如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=,△ADC与△ABC关于AC所在的直线对称.
(1)当OB=2时,求∠ACB度数及点D的坐标;
(2)若点A和点D在同一个反比例函数的图象上,求OB的长;
(3)如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数(k≠0)的图象与BA的延长线交于点P.问:
①连接PA,AA,则∠AAP=
°;
②在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
6.如图,已知函数的图象经过点点的坐标为.过点作轴,(点位于点的下方),过点作轴,与函数的图象交于点,过点作,垂足在线段上,连接.
求的面积;
当时,求的长.
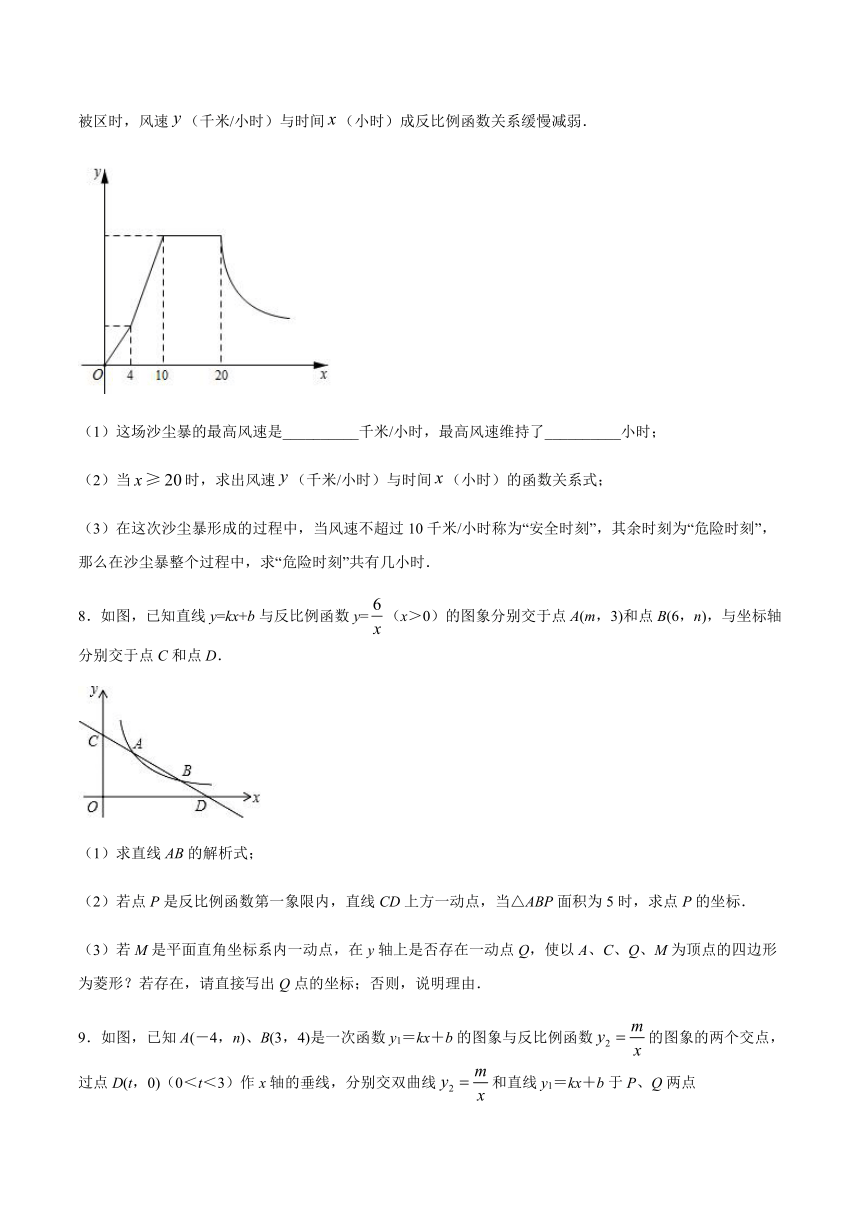
7.某气象研究中心观测到一场沙尘暴从发生到减弱的全过程.开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速(千米/小时)与时间(小时)成反比例函数关系缓慢减弱.
(1)这场沙尘暴的最高风速是__________千米/小时,最高风速维持了__________小时;
(2)当时,求出风速(千米/小时)与时间(小时)的函数关系式;
(3)在这次沙尘暴形成的过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻为“危险时刻”,那么在沙尘暴整个过程中,求“危险时刻”共有几小时.
8.如图,已知直线y=kx+b与反比例函数y=(x>0)的图象分别交于点A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是反比例函数第一象限内,直线CD上方一动点,当△ABP面积为5时,求点P的坐标.
(3)若M是平面直角坐标系内一动点,在y轴上是否存在一动点Q,使以A、C、Q、M为顶点的四边形为菱形?若存在,请直接写出Q点的坐标;否则,说明理由.
9.如图,已知A(-4,n)、B(3,4)是一次函数y1=kx+b的图象与反比例函数的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线和直线y1=kx+b于P、Q两点
(1)
直接写出反比例函数和一次函数的解析式
(2)
当t为何值时,S△BPQ=S△APQ
(3)
以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线(x>0)始终有交点
10.如图,一次函数的图象与反比例函数的图象相交于、两点,其中点的坐标为,点的坐标为.
(1)根据图象,直接写出满足的的取值范围;
(2)求这两个函数的表达式;
(3)点在线段上,且,求点的坐标.
11.如图,点A、B是反比例函数y=的图像上的两个动点,过A、B分别作AC⊥x轴、BD⊥x轴,分别交反比例函数y=-的图像于点C、D,四边形ACBD是平行四边形.
(1)若点A的横坐标为-4.
①直接写出线段AC的长度;
②求出点B的坐标;
(2)当点A、B不断运动时,下列关于□ACBD的结论:①□ACBD可能是矩形;②□ACBD可能是菱形;③□ACBD可能是正方形;④□ACBD的周长始终不变;⑤□ACBD的面积始终不变.其中所有正确结论的序号是
.
12.如图,在平面直角坐标系中,点在反比例函数的图象上,点在的延长线上,轴,垂足为与反比例函数的图象相交于点,连接.
(1)求该反比例函数的解析式;
(2)当点时,求;
(3)若,则线段________.
13.如图,正比例函数的图像与反比例函数的图像交于点.点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图像于点C,交正比例函数的图像于点D.
(1)求a的值及正比例函数的表达式;
(2)若,求的面积.
14.如图,在平面直角坐标系中,矩形的顶点在轴的正半轴上,顶点在轴的正半轴上,是边上的一点,,.反比例函数在第一象限内的图像经过点,交于点,.
(1)求这个反比例函数的表达式,
(2)动点在矩形内,且满足.
①若点在这个反比例函数的图像上,求点的坐标,
②若点是平面内一点,使得以、、、为顶点的四边形是菱形,求点的坐标.
15.如图,矩形的顶点分别在轴的正半轴上,点在反比例函数的第一象限内的图像上,,动点在轴的上方,且满足.
(1)若点在这个反比例函数的图像上,求点的坐标;
(2)连接,求的最小值;
(3)若点是平面内一点,使得以为顶点的四边形是菱形,则请你直接写出满足条件的所有点的坐标.
16.如图,一次函数的图象与轴、轴分别交于、两点,与反比例函数交于点,过点分别作轴、轴的垂线,垂足分别为点、.若,,.
(1)求点的坐标;
(2)求一次函数和反比例函数的表达式.
17.如图,已知点A.B在双曲线y=
?(x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
(1)设A的横坐标为m,试用m、k表示B的坐标.
(2)试判断四边形ABCD的形状,并说明理由.
(3)若△ABP的面积为3,求该双曲线的解析式.
18.如图,的直角边OB在x轴的正半轴上,反比例函数的图象经过斜边OA的中点D,与直角边AB相交于点C.
①若点,求点C的坐标:
②若,求k的值.
19.如图,在平面直角坐标系中,A
(6,0)、B(0,
4)是矩形OACB的两个顶点,双曲线(k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线的另一个交点,
(1)点D的坐标为
,点E的坐标为
.
(2)动点P在第一象限内,且满足.
①若点P在这个反比例函数的图像上,求点P的坐标;
②连接PO、PE,当PO-PE的值最大时,求点P的坐标;
③若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
20.如图所示,一次函数y=kx+b的图象与反比例函数y交于A(1,t+2),B(﹣2t,﹣1)两点.
(1)求一次函数和反比例函数的函数表达式;
(2)点C(x1,y1)和D(x2,y2)是反比例函数y图象上任意两点,
①若x1<x2<0,p,q,试判断p、q的大小关系,并说明理由;
②若x1<﹣4,0<x2<1,过C、D两点分别作直线AB的垂线,垂足分别为E、F,当x1x2=﹣4时,判断四边形CEFD的形状,并说明理由.
21.如图1,矩形的边OA在x轴上,边OC在y轴上,函数(k>0,x>0)的图象与BC边相交于点M(点M不与点B、C重合),与AB边相交于点N,.
(1)若点B的坐标为(4,2),i=0.5,求k的值和点N的坐标;
(2)连接OB,过M作MQ⊥OB,垂足为Q;
①如图2.当k=1,时,设OB长为p,MQ长为q,求p与q的函数关系式;
②如图3,连接NQ,记四边形OANQ,△NQB,△QBM,四边形MCOQ的面积分别为S1、S2、S3、S4.判断S1+S3与S2+S4的数量关系,并说明理由.
22.如图,点A是坐标原点,点D是反比例函数y=(x>0)图象上一点,点B在x轴上,AD=BD,四边形ABCD是平行四边形,BC交反比例函数y=(x>0)图象于点E.
(1)平行四边形ABCD的面积等于
,
(2)设D点横坐标为m,
①试用m表示点C的坐标;
②试用m表示点E的坐标.(要有推理和计算过程)
(3)求CE:EB的值.
(4)求EB的最小值.
23.如图1,直线y=x-1交x轴、y轴于A、B点,点P(1,,且S四边形PAOB=3.5,双曲线y=经过点P.
(1)求k的值;
(2)如图2,直线)交射线BA于E,交双曲线y=于F,将直线向右平移4个单位长度后交射线于,交双曲线y=于,若,求的值.
24.已知直线y=2x+b与反比例函数y=的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E,
(1)若k=8,且点A的横坐标为1,求b的值;
(2)已知△BEC的面积为4,则k的值为多少?
(3)若将直线旋转,k=8,点E为△ABC的重心且OE=2,求直线AC的解析式.
25.如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(?3,0),B(0,1)
(1)将△ABC沿x轴的正方向平移t个单位,B、C两点的对应点B′、C′正好落在反比例函数y=的图象上.请直接写出C点的坐标和t,k的值;
(2)有一个Rt△DEF,∠D=90°,∠E=60°,DE=2,将它放在直角坐标系中,使斜边EF在x轴上,直角顶点D在(1)中的反比例函数图象上,求点F的坐标;
参考答案
1.(1),;(2)或;(3)(0,-1)或
(2,-1).
2.(1)k=8;(2)-4≤x<0或x≥4;(3);(4)M(3,0),N(0,6)或M′(-3,0),N′(0,-6).
3.(1)m=12,n=3;(2)y=x+6
4.(1)3;(2);(3)或
5.(1)60°;(2)3(3)①30②存在;,
6.(1);(2)
7.(1)32,10;(2);(3)共有59.5小时
8.(1)直线AB的解析式为y=﹣x+4;(2)点P的坐标为(1,6)或(12,);(3)存在,点Q的坐标为(0,2)或(0,4+)或(0,4﹣)或(0,1.5)
9.(1);(2);(3)见解析
10.(1)或;(2),;(3)
11.(1)①AC的长度为2.5;②(4,2);(2)②⑤
12.(1);(2);(3)
13.(1)a=2;y=2x;(2)
14.(1);(2)①
;②
15.(1)点P的坐标为(6,2);(2);(3)Q
(4?,5),Q
(4+,5),Q
(4?2,?1),Q
(4+2,?1).
16.(1);(2).
17.(1)B(2m,);(2)四边形ABCD是菱形,理由见解析;(3)y=
.
19.(1)(6,2),(3,4);(2)①;②;③、、、.
20.(1)y,y=x+3;(2)①p<q,理由见解析;②四边形CEFD为矩形,理由见解析.
21.(1)9;(6,1)
(2)①②S1+S3与S2+S4,证明见解析
22.(1)12;(2)①C(3m,),②
E(,);(3);(4)2﹣2
23.(1);
(2)
24.(1)b=6;(2)k=8;(3)直线AC的解析式为y=2x+4.
25.(1)C(?4,3),t=6,k=6;(2)满足条件的点F的坐标为(?3,0)或(+3,0);(3)存在,
1.如图,平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=(k≠0)的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1>y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若AD=3CD,求点C的坐标.
2.如图,已知直线与双曲线交于、两点,点横坐标为4.
(1)求值;
(2)直接写出关于的不等式的解集;
(3)若双曲线上有一点的纵坐标为8,求的面积;
(4)若在轴上有点,轴上有点,且点、、、四点恰好构成平行四边形,直接写出点、的坐标.
3.如图,函数与函数的图像相交于点.点在函数的图像上,过点作轴,与轴相交于点,且.
(1)求的值;
(2)求直线的函数表达式.
4.如图,直线都与双曲线
交于点,这两条直线分别与
x轴交于B,C两点.
(1)试确定k的值;
(2)直接写出当时,不等式的解集;
(3)若点P在x轴上,连接,把的面积分成两部分,求此时点
P的坐标.
5.如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=,△ADC与△ABC关于AC所在的直线对称.
(1)当OB=2时,求∠ACB度数及点D的坐标;
(2)若点A和点D在同一个反比例函数的图象上,求OB的长;
(3)如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数(k≠0)的图象与BA的延长线交于点P.问:
①连接PA,AA,则∠AAP=
°;
②在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
6.如图,已知函数的图象经过点点的坐标为.过点作轴,(点位于点的下方),过点作轴,与函数的图象交于点,过点作,垂足在线段上,连接.
求的面积;
当时,求的长.
7.某气象研究中心观测到一场沙尘暴从发生到减弱的全过程.开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速(千米/小时)与时间(小时)成反比例函数关系缓慢减弱.
(1)这场沙尘暴的最高风速是__________千米/小时,最高风速维持了__________小时;
(2)当时,求出风速(千米/小时)与时间(小时)的函数关系式;
(3)在这次沙尘暴形成的过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻为“危险时刻”,那么在沙尘暴整个过程中,求“危险时刻”共有几小时.
8.如图,已知直线y=kx+b与反比例函数y=(x>0)的图象分别交于点A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是反比例函数第一象限内,直线CD上方一动点,当△ABP面积为5时,求点P的坐标.
(3)若M是平面直角坐标系内一动点,在y轴上是否存在一动点Q,使以A、C、Q、M为顶点的四边形为菱形?若存在,请直接写出Q点的坐标;否则,说明理由.
9.如图,已知A(-4,n)、B(3,4)是一次函数y1=kx+b的图象与反比例函数的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线和直线y1=kx+b于P、Q两点
(1)
直接写出反比例函数和一次函数的解析式
(2)
当t为何值时,S△BPQ=S△APQ
(3)
以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线(x>0)始终有交点
10.如图,一次函数的图象与反比例函数的图象相交于、两点,其中点的坐标为,点的坐标为.
(1)根据图象,直接写出满足的的取值范围;
(2)求这两个函数的表达式;
(3)点在线段上,且,求点的坐标.
11.如图,点A、B是反比例函数y=的图像上的两个动点,过A、B分别作AC⊥x轴、BD⊥x轴,分别交反比例函数y=-的图像于点C、D,四边形ACBD是平行四边形.
(1)若点A的横坐标为-4.
①直接写出线段AC的长度;
②求出点B的坐标;
(2)当点A、B不断运动时,下列关于□ACBD的结论:①□ACBD可能是矩形;②□ACBD可能是菱形;③□ACBD可能是正方形;④□ACBD的周长始终不变;⑤□ACBD的面积始终不变.其中所有正确结论的序号是
.
12.如图,在平面直角坐标系中,点在反比例函数的图象上,点在的延长线上,轴,垂足为与反比例函数的图象相交于点,连接.
(1)求该反比例函数的解析式;
(2)当点时,求;
(3)若,则线段________.
13.如图,正比例函数的图像与反比例函数的图像交于点.点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图像于点C,交正比例函数的图像于点D.
(1)求a的值及正比例函数的表达式;
(2)若,求的面积.
14.如图,在平面直角坐标系中,矩形的顶点在轴的正半轴上,顶点在轴的正半轴上,是边上的一点,,.反比例函数在第一象限内的图像经过点,交于点,.
(1)求这个反比例函数的表达式,
(2)动点在矩形内,且满足.
①若点在这个反比例函数的图像上,求点的坐标,
②若点是平面内一点,使得以、、、为顶点的四边形是菱形,求点的坐标.
15.如图,矩形的顶点分别在轴的正半轴上,点在反比例函数的第一象限内的图像上,,动点在轴的上方,且满足.
(1)若点在这个反比例函数的图像上,求点的坐标;
(2)连接,求的最小值;
(3)若点是平面内一点,使得以为顶点的四边形是菱形,则请你直接写出满足条件的所有点的坐标.
16.如图,一次函数的图象与轴、轴分别交于、两点,与反比例函数交于点,过点分别作轴、轴的垂线,垂足分别为点、.若,,.
(1)求点的坐标;
(2)求一次函数和反比例函数的表达式.
17.如图,已知点A.B在双曲线y=
?(x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
(1)设A的横坐标为m,试用m、k表示B的坐标.
(2)试判断四边形ABCD的形状,并说明理由.
(3)若△ABP的面积为3,求该双曲线的解析式.
18.如图,的直角边OB在x轴的正半轴上,反比例函数的图象经过斜边OA的中点D,与直角边AB相交于点C.
①若点,求点C的坐标:
②若,求k的值.
19.如图,在平面直角坐标系中,A
(6,0)、B(0,
4)是矩形OACB的两个顶点,双曲线(k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线的另一个交点,
(1)点D的坐标为
,点E的坐标为
.
(2)动点P在第一象限内,且满足.
①若点P在这个反比例函数的图像上,求点P的坐标;
②连接PO、PE,当PO-PE的值最大时,求点P的坐标;
③若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
20.如图所示,一次函数y=kx+b的图象与反比例函数y交于A(1,t+2),B(﹣2t,﹣1)两点.
(1)求一次函数和反比例函数的函数表达式;
(2)点C(x1,y1)和D(x2,y2)是反比例函数y图象上任意两点,
①若x1<x2<0,p,q,试判断p、q的大小关系,并说明理由;
②若x1<﹣4,0<x2<1,过C、D两点分别作直线AB的垂线,垂足分别为E、F,当x1x2=﹣4时,判断四边形CEFD的形状,并说明理由.
21.如图1,矩形的边OA在x轴上,边OC在y轴上,函数(k>0,x>0)的图象与BC边相交于点M(点M不与点B、C重合),与AB边相交于点N,.
(1)若点B的坐标为(4,2),i=0.5,求k的值和点N的坐标;
(2)连接OB,过M作MQ⊥OB,垂足为Q;
①如图2.当k=1,时,设OB长为p,MQ长为q,求p与q的函数关系式;
②如图3,连接NQ,记四边形OANQ,△NQB,△QBM,四边形MCOQ的面积分别为S1、S2、S3、S4.判断S1+S3与S2+S4的数量关系,并说明理由.
22.如图,点A是坐标原点,点D是反比例函数y=(x>0)图象上一点,点B在x轴上,AD=BD,四边形ABCD是平行四边形,BC交反比例函数y=(x>0)图象于点E.
(1)平行四边形ABCD的面积等于
,
(2)设D点横坐标为m,
①试用m表示点C的坐标;
②试用m表示点E的坐标.(要有推理和计算过程)
(3)求CE:EB的值.
(4)求EB的最小值.
23.如图1,直线y=x-1交x轴、y轴于A、B点,点P(1,,且S四边形PAOB=3.5,双曲线y=经过点P.
(1)求k的值;
(2)如图2,直线)交射线BA于E,交双曲线y=于F,将直线向右平移4个单位长度后交射线于,交双曲线y=于,若,求的值.
24.已知直线y=2x+b与反比例函数y=的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E,
(1)若k=8,且点A的横坐标为1,求b的值;
(2)已知△BEC的面积为4,则k的值为多少?
(3)若将直线旋转,k=8,点E为△ABC的重心且OE=2,求直线AC的解析式.
25.如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(?3,0),B(0,1)
(1)将△ABC沿x轴的正方向平移t个单位,B、C两点的对应点B′、C′正好落在反比例函数y=的图象上.请直接写出C点的坐标和t,k的值;
(2)有一个Rt△DEF,∠D=90°,∠E=60°,DE=2,将它放在直角坐标系中,使斜边EF在x轴上,直角顶点D在(1)中的反比例函数图象上,求点F的坐标;
参考答案
1.(1),;(2)或;(3)(0,-1)或
(2,-1).
2.(1)k=8;(2)-4≤x<0或x≥4;(3);(4)M(3,0),N(0,6)或M′(-3,0),N′(0,-6).
3.(1)m=12,n=3;(2)y=x+6
4.(1)3;(2);(3)或
5.(1)60°;(2)3(3)①30②存在;,
6.(1);(2)
7.(1)32,10;(2);(3)共有59.5小时
8.(1)直线AB的解析式为y=﹣x+4;(2)点P的坐标为(1,6)或(12,);(3)存在,点Q的坐标为(0,2)或(0,4+)或(0,4﹣)或(0,1.5)
9.(1);(2);(3)见解析
10.(1)或;(2),;(3)
11.(1)①AC的长度为2.5;②(4,2);(2)②⑤
12.(1);(2);(3)
13.(1)a=2;y=2x;(2)
14.(1);(2)①
;②
15.(1)点P的坐标为(6,2);(2);(3)Q
(4?,5),Q
(4+,5),Q
(4?2,?1),Q
(4+2,?1).
16.(1);(2).
17.(1)B(2m,);(2)四边形ABCD是菱形,理由见解析;(3)y=
.
19.(1)(6,2),(3,4);(2)①;②;③、、、.
20.(1)y,y=x+3;(2)①p<q,理由见解析;②四边形CEFD为矩形,理由见解析.
21.(1)9;(6,1)
(2)①②S1+S3与S2+S4,证明见解析
22.(1)12;(2)①C(3m,),②
E(,);(3);(4)2﹣2
23.(1);
(2)
24.(1)b=6;(2)k=8;(3)直线AC的解析式为y=2x+4.
25.(1)C(?4,3),t=6,k=6;(2)满足条件的点F的坐标为(?3,0)或(+3,0);(3)存在,
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
