9.2.1 总体取值规律的估计【新教材】人教A版(2019)高中数学必修第二册
文档属性
| 名称 | 9.2.1 总体取值规律的估计【新教材】人教A版(2019)高中数学必修第二册 |  | |
| 格式 | zip | ||
| 文件大小 | 424.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 10:31:30 | ||
图片预览


文档简介
9.2 用样本估计总体
9.2.1 总体取值规律的估计
课标解读
课标要求
核心素养
1.会根据实际问题的特点,选择恰当的统计图表对数据进行可视化描述,体会合理使用统计图表的重要性.
2.结合实例,能用样本估计总体的取值规律.
1.通过对统计图表的读图和识图,培养学生直观想象的核心素养.
2.通过应用统计图表估计总体的取值规律,培养学生数据分析的核心素养.
以下是某学校高一(2)班学生一次政治考试的成绩.
76 83 88 89 72 67 88 85 90 87 74 65 86 71 88
90 82 90 81 78 76 75 78 86 79 71 73 82 76 90
77 81 83 77 93 94 84 70 77 89 83 84 68 74 59
77 86 89 78 86 76 85 83 69 81 84 90 85 76 79
问题1:你能否很容易地从以上这些数据中看出其分布规律?
问题2:怎样才能直观地表示出上述数据的大致分布情况(比如指出哪个分数段的分数比较多,哪个分数段的分数比较少)?
1.画频率分布直方图的步骤
(1)求极差:极差为一组数据中①最大值与②最小值的差;
(2)决定组距与组数:当样本容量不超过100时,常分成③5~12组,为方便起见,一般取等长组距,并且组距应力求“取整”;
(3)将数据分组;
(4)列频率分布表:一般分四列:分组、④频数累计、频数、⑤频率.其中频数合计应是样本容量,频率合计是⑥1;
(5)画频率分布直方图:横轴表示分组,纵轴表示⑦.
小长方形的面积=组距×⑧=⑨频率,各小长方形的面积的总和等于1.
思考1:为什么要对样本数据进行分组?
提示 不分组很难看出样本中的数字所包含的信息,分组后,计算出频率,从而估计总体的分布特征.
思考2:频数分布表与频率分布直方图有什么不同?
提示 频数分布表能使我们清楚地知道数据分布在各个小组的个数,而频率分布直方图则是从各个小组数据在样本容量中所占比例大小的角度来表示数据分布的规律.
2.其他统计图表
统计图表
主要应用
扇形图
直观描述各部分数据在全部数据中所占的比例
条形图和直方图
直观描述不同类别或分组数据的频数和频率
折线图
反映统计对象在不同时间(或其他合适情形)的发展变化情况
探究一 频率分布直方图的绘制
例1 为加强中学生实践创新能力和团队精神的培养,促进教育教学改革,某市教育局将举办全市中学生创新知识竞赛.某校举行选拔赛,共有200名学生参加,为了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表解答下列问题:
分组
频数
频率
[60,70)
a
0.26
[70,80)
15
c
[80,90)
18
0.36
[90,100]
b
d
合计
50
e
(1)求a,b,c,d,e的值;
(2)作出频率分布直方图.
1-1 有一容量为50的样本,数据的分组及各组的频数如下:[10,15),4;[15,20),5;[20,25),10;[25,30),11;[30,35),9;[35,40),8;[40,45],3.
(1)列出样本频率分布表;
(2)画出频率分布直方图.
探究二 频率分布直方图的相关计算
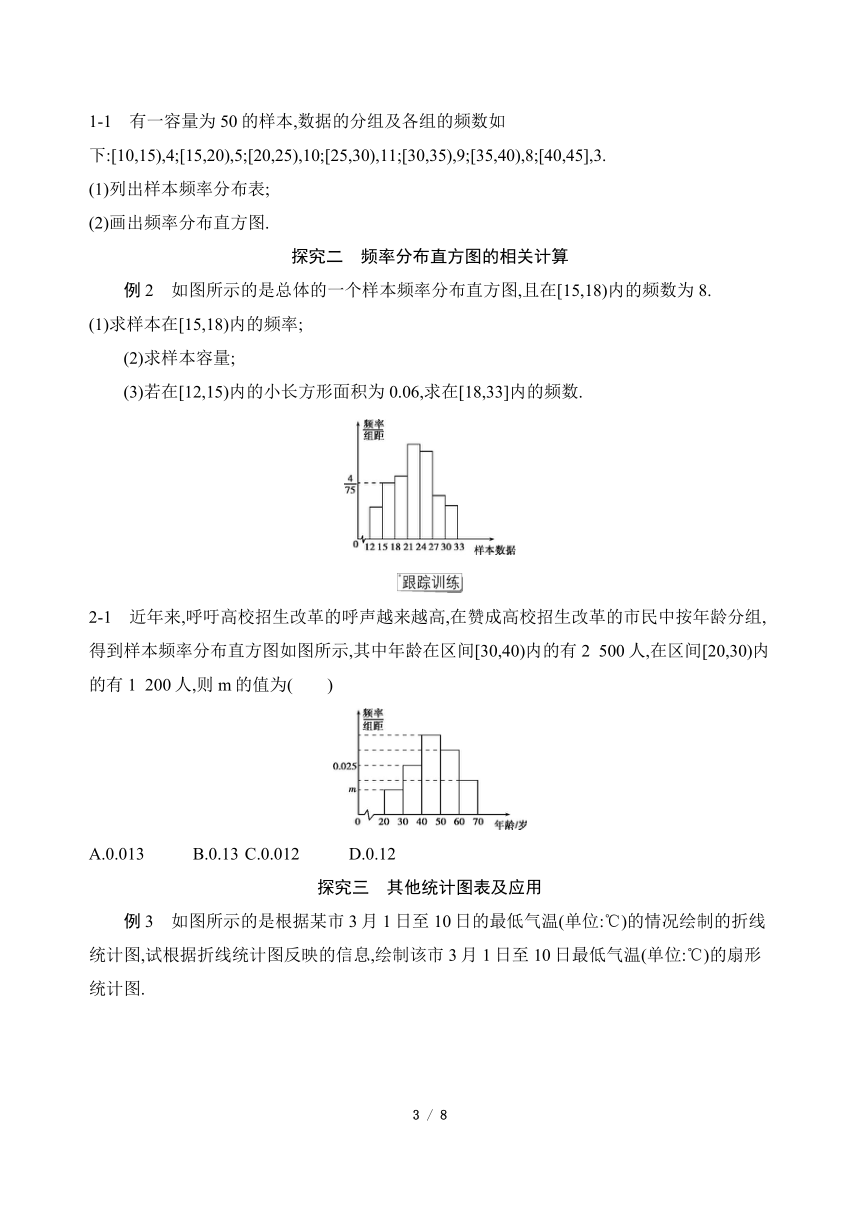
例2 如图所示的是总体的一个样本频率分布直方图,且在[15,18)内的频数为8.
(1)求样本在[15,18)内的频率;
(2)求样本容量;
(3)若在[12,15)内的小长方形面积为0.06,求在[18,33]内的频数.
2-1 近年来,呼吁高校招生改革的呼声越来越高,在赞成高校招生改革的市民中按年龄分组,得到样本频率分布直方图如图所示,其中年龄在区间[30,40)内的有2
500人,在区间[20,30)内的有1
200人,则m的值为( )
A.0.013
B.0.13
C.0.012
D.0.12
探究三 其他统计图表及应用
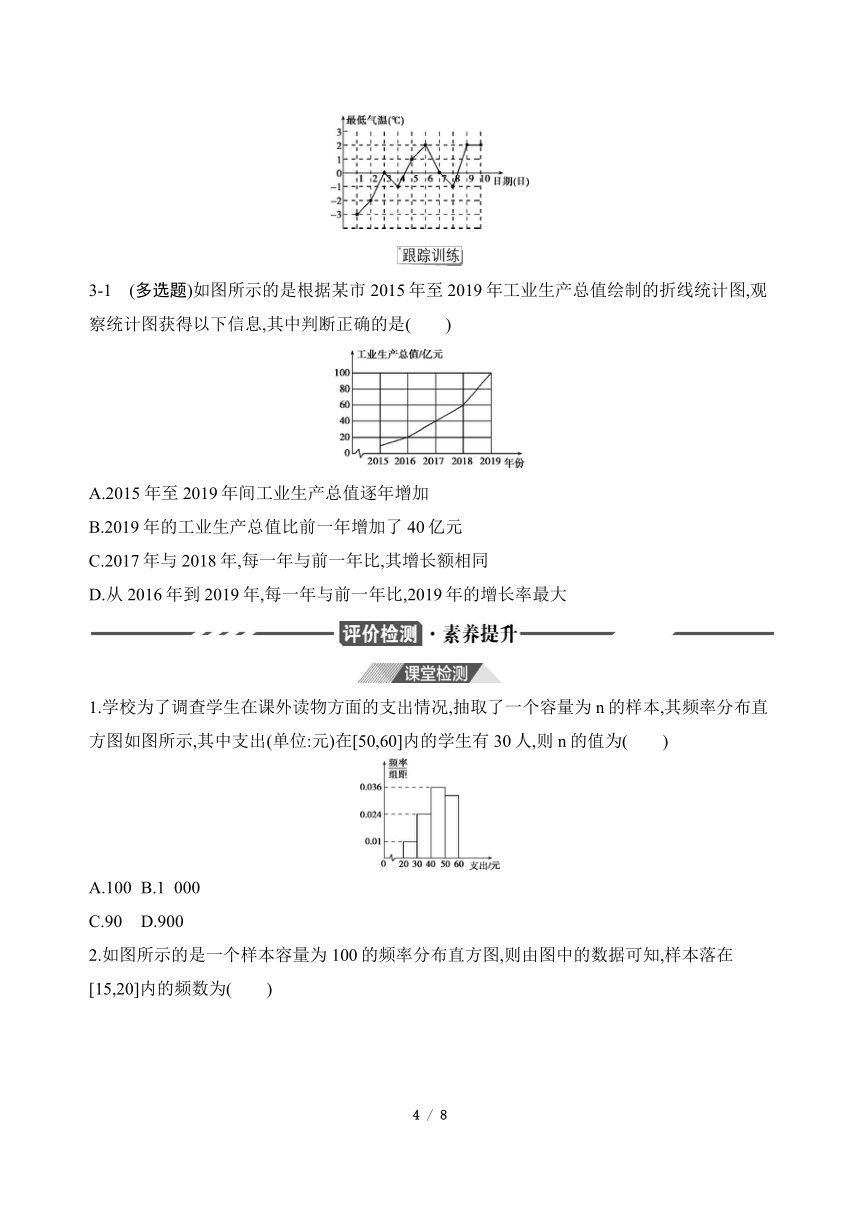
例3 如图所示的是根据某市3月1日至10日的最低气温(单位:℃)的情况绘制的折线统计图,试根据折线统计图反映的信息,绘制该市3月1日至10日最低气温(单位:℃)的扇形统计图.
3-1 (多选题)如图所示的是根据某市2015年至2019年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中判断正确的是( )
A.2015年至2019年间工业生产总值逐年增加
B.2019年的工业生产总值比前一年增加了40亿元
C.2017年与2018年,每一年与前一年比,其增长额相同
D.从2016年到2019年,每一年与前一年比,2019年的增长率最大
1.学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图所示,其中支出(单位:元)在[50,60]内的学生有30人,则n的值为( )
A.100
B.1
000
C.90
D.900
2.如图所示的是一个样本容量为100的频率分布直方图,则由图中的数据可知,样本落在[15,20]内的频数为( )
A.20
B.30
C.40
D.50
3.下图是某市连续7天的最高气温与最低气温的变化图,根据图中信息可知,这7天中最大的日温差是 ℃.?
1.下图是甲、乙、丙、丁四组人数的扇形统计图的部分结果,根据扇形统计图的情况可以知道丙、丁两组人数和为( )
A.250
B.150
C.400
D.300
2.容量为100的样本数据,按从小到大的顺序分为8组,如下表:
组号
1
2
3
4
5
6
7
8
频数
10
13
x
14
15
13
12
9
第3组的频数和频率分别是( )
A.14和0.14
B.0.14和14
C.和0.14
D.和
3.已知某地区中小学生人数和近视情况分别如图甲和图乙所示.为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
A.100,20
B.200,20
C.200,10
D.100,10
4.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.搜索指数越大,表示网民搜索该关键词的次数越多,对该关键词相关的信息关注度也越高.下图是2018年9月到2019年2月这半年来对某个关键词的搜索指数变化的统计图.
根据该统计图判断,下列结论正确的是( )
A.这半年来,网民对该关键词相关的信息关注度呈周期性变化
B.这半年来,网民对该关键词相关的信息关注度不断减弱
C.从该关键词的搜索指数来看,2018年10月的方差小于11月的方差
D.从该关键词的搜索指数来看,2018年12月的平均值大于2019年1月的平均值
5.某班计划开展一些课外活动,全班有40名学生报名参加,他们就乒乓球、足球、跳绳、羽毛球4项活动的参加人数做了统计,绘制了条形统计图(如图所示),那么参加羽毛球活动的人数的频率是 .?
6.在样本的频率分布直方图中,共有5个小长方形,已知中间一个小长方形面积是其余4个小长方形面积之和的,且中间一组的频数为10,则这个样本容量是 .?
7.(多选题)为了了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重(单位:kg)情况如三维饼图(1)所示,经过四个月的健身后,他们的体重情况如三维饼图(2)所示.
对比健身前后,关于这20名肥胖者,下面结论正确的是( )
A.他们健身后,体重在区间[90,100)内增加了2人
B.他们健身后,体重在区间[100,110)内的人数没有改变
C.他们健身后,20人的平均体重大约减少了8
kg
D.他们健身后,原来体重在区间[110,120)内的肥胖者体重都有减少
8.从某小学随机抽取100名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图所示),由图中数据可知a= .若要从身高在[120,130),[130,140),[140,150]这三组内的学生中,用分层随机抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中抽取的人数为 .?
9.某省的有关部门要求各中小学要把“每天锻炼一小时”写入课程表,为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图.请结合统计图回答下列问题:
图1
图2
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数为多少?
16
/
17
9.2.1 总体取值规律的估计
课标解读
课标要求
核心素养
1.会根据实际问题的特点,选择恰当的统计图表对数据进行可视化描述,体会合理使用统计图表的重要性.
2.结合实例,能用样本估计总体的取值规律.
1.通过对统计图表的读图和识图,培养学生直观想象的核心素养.
2.通过应用统计图表估计总体的取值规律,培养学生数据分析的核心素养.
以下是某学校高一(2)班学生一次政治考试的成绩.
76 83 88 89 72 67 88 85 90 87 74 65 86 71 88
90 82 90 81 78 76 75 78 86 79 71 73 82 76 90
77 81 83 77 93 94 84 70 77 89 83 84 68 74 59
77 86 89 78 86 76 85 83 69 81 84 90 85 76 79
问题1:你能否很容易地从以上这些数据中看出其分布规律?
问题2:怎样才能直观地表示出上述数据的大致分布情况(比如指出哪个分数段的分数比较多,哪个分数段的分数比较少)?
1.画频率分布直方图的步骤
(1)求极差:极差为一组数据中①最大值与②最小值的差;
(2)决定组距与组数:当样本容量不超过100时,常分成③5~12组,为方便起见,一般取等长组距,并且组距应力求“取整”;
(3)将数据分组;
(4)列频率分布表:一般分四列:分组、④频数累计、频数、⑤频率.其中频数合计应是样本容量,频率合计是⑥1;
(5)画频率分布直方图:横轴表示分组,纵轴表示⑦.
小长方形的面积=组距×⑧=⑨频率,各小长方形的面积的总和等于1.
思考1:为什么要对样本数据进行分组?
提示 不分组很难看出样本中的数字所包含的信息,分组后,计算出频率,从而估计总体的分布特征.
思考2:频数分布表与频率分布直方图有什么不同?
提示 频数分布表能使我们清楚地知道数据分布在各个小组的个数,而频率分布直方图则是从各个小组数据在样本容量中所占比例大小的角度来表示数据分布的规律.
2.其他统计图表
统计图表
主要应用
扇形图
直观描述各部分数据在全部数据中所占的比例
条形图和直方图
直观描述不同类别或分组数据的频数和频率
折线图
反映统计对象在不同时间(或其他合适情形)的发展变化情况
探究一 频率分布直方图的绘制
例1 为加强中学生实践创新能力和团队精神的培养,促进教育教学改革,某市教育局将举办全市中学生创新知识竞赛.某校举行选拔赛,共有200名学生参加,为了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表解答下列问题:
分组
频数
频率
[60,70)
a
0.26
[70,80)
15
c
[80,90)
18
0.36
[90,100]
b
d
合计
50
e
(1)求a,b,c,d,e的值;
(2)作出频率分布直方图.
1-1 有一容量为50的样本,数据的分组及各组的频数如下:[10,15),4;[15,20),5;[20,25),10;[25,30),11;[30,35),9;[35,40),8;[40,45],3.
(1)列出样本频率分布表;
(2)画出频率分布直方图.
探究二 频率分布直方图的相关计算
例2 如图所示的是总体的一个样本频率分布直方图,且在[15,18)内的频数为8.
(1)求样本在[15,18)内的频率;
(2)求样本容量;
(3)若在[12,15)内的小长方形面积为0.06,求在[18,33]内的频数.
2-1 近年来,呼吁高校招生改革的呼声越来越高,在赞成高校招生改革的市民中按年龄分组,得到样本频率分布直方图如图所示,其中年龄在区间[30,40)内的有2
500人,在区间[20,30)内的有1
200人,则m的值为( )
A.0.013
B.0.13
C.0.012
D.0.12
探究三 其他统计图表及应用
例3 如图所示的是根据某市3月1日至10日的最低气温(单位:℃)的情况绘制的折线统计图,试根据折线统计图反映的信息,绘制该市3月1日至10日最低气温(单位:℃)的扇形统计图.
3-1 (多选题)如图所示的是根据某市2015年至2019年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中判断正确的是( )
A.2015年至2019年间工业生产总值逐年增加
B.2019年的工业生产总值比前一年增加了40亿元
C.2017年与2018年,每一年与前一年比,其增长额相同
D.从2016年到2019年,每一年与前一年比,2019年的增长率最大
1.学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图所示,其中支出(单位:元)在[50,60]内的学生有30人,则n的值为( )
A.100
B.1
000
C.90
D.900
2.如图所示的是一个样本容量为100的频率分布直方图,则由图中的数据可知,样本落在[15,20]内的频数为( )
A.20
B.30
C.40
D.50
3.下图是某市连续7天的最高气温与最低气温的变化图,根据图中信息可知,这7天中最大的日温差是 ℃.?
1.下图是甲、乙、丙、丁四组人数的扇形统计图的部分结果,根据扇形统计图的情况可以知道丙、丁两组人数和为( )
A.250
B.150
C.400
D.300
2.容量为100的样本数据,按从小到大的顺序分为8组,如下表:
组号
1
2
3
4
5
6
7
8
频数
10
13
x
14
15
13
12
9
第3组的频数和频率分别是( )
A.14和0.14
B.0.14和14
C.和0.14
D.和
3.已知某地区中小学生人数和近视情况分别如图甲和图乙所示.为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
A.100,20
B.200,20
C.200,10
D.100,10
4.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.搜索指数越大,表示网民搜索该关键词的次数越多,对该关键词相关的信息关注度也越高.下图是2018年9月到2019年2月这半年来对某个关键词的搜索指数变化的统计图.
根据该统计图判断,下列结论正确的是( )
A.这半年来,网民对该关键词相关的信息关注度呈周期性变化
B.这半年来,网民对该关键词相关的信息关注度不断减弱
C.从该关键词的搜索指数来看,2018年10月的方差小于11月的方差
D.从该关键词的搜索指数来看,2018年12月的平均值大于2019年1月的平均值
5.某班计划开展一些课外活动,全班有40名学生报名参加,他们就乒乓球、足球、跳绳、羽毛球4项活动的参加人数做了统计,绘制了条形统计图(如图所示),那么参加羽毛球活动的人数的频率是 .?
6.在样本的频率分布直方图中,共有5个小长方形,已知中间一个小长方形面积是其余4个小长方形面积之和的,且中间一组的频数为10,则这个样本容量是 .?
7.(多选题)为了了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重(单位:kg)情况如三维饼图(1)所示,经过四个月的健身后,他们的体重情况如三维饼图(2)所示.
对比健身前后,关于这20名肥胖者,下面结论正确的是( )
A.他们健身后,体重在区间[90,100)内增加了2人
B.他们健身后,体重在区间[100,110)内的人数没有改变
C.他们健身后,20人的平均体重大约减少了8
kg
D.他们健身后,原来体重在区间[110,120)内的肥胖者体重都有减少
8.从某小学随机抽取100名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图所示),由图中数据可知a= .若要从身高在[120,130),[130,140),[140,150]这三组内的学生中,用分层随机抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中抽取的人数为 .?
9.某省的有关部门要求各中小学要把“每天锻炼一小时”写入课程表,为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图.请结合统计图回答下列问题:
图1
图2
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数为多少?
16
/
17
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
