18.2.2函数图象
图片预览




文档简介
(共12张PPT)
18.2.2 函数的图象
知识回顾
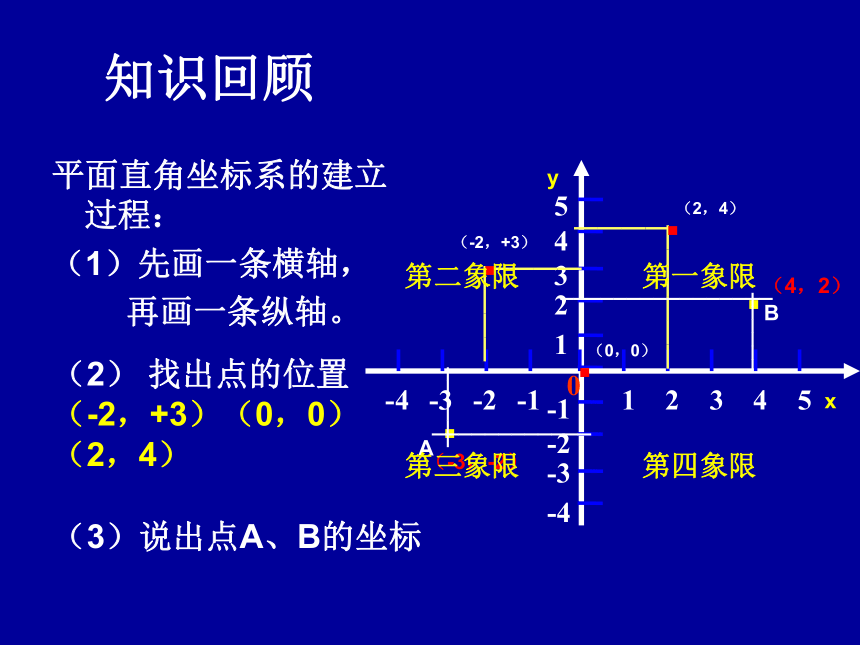
平面直角坐标系的建立过程:
(1)先画一条横轴,
再画一条纵轴。
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
(2) 找出点的位置
(-2,+3)(0,0)(2,4)
————
————
·
(-2,+3)
·
(0,0)
——————
————
·
(2,4)
·
·
A
B
(3)说出点A、B的坐标
(-3,-2)
(4,2)
第一象限
第二象限
第三象限
第四象限
______
____________
______
________________
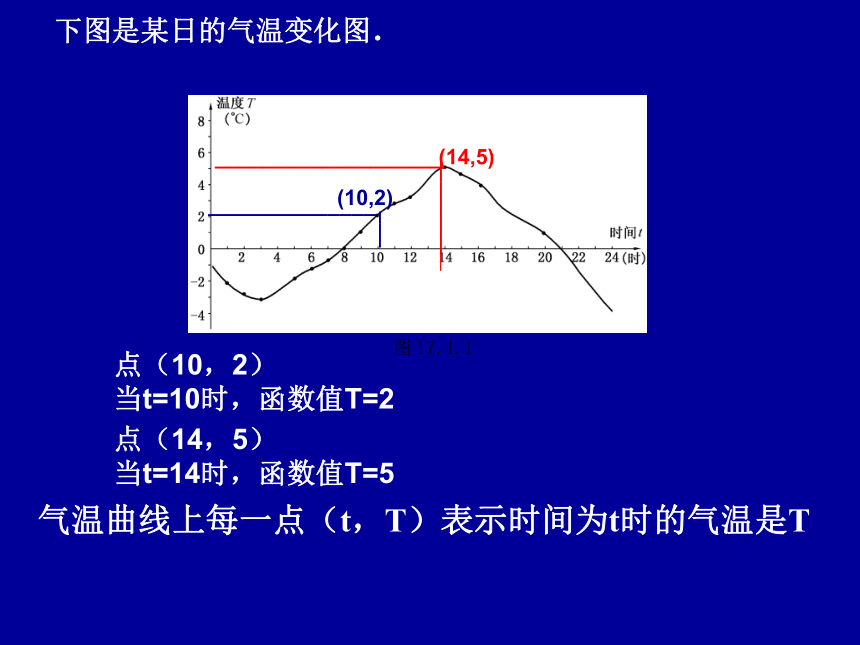
下图是某日的气温变化图.
气温曲线上每一点(t,T)表示时间为t时的气温是T
点(10,2)
当t=10时,函数值T=2
点(14,5)
当t=14时,函数值T=5
______________
___
(10,2)
___________________
(14,5)
________
探究新知
问题:气温曲线是图象表示函数的一个实际例子。那么什么是函数图象呢?
一般来说,函数的图象是由直角坐标系中的一系列点组成,图象上的每一点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与它对应的函数值。
解:取自变量x的一些值,例如x=-3,-2,-1,0,1,2,3 …,计算出对应的函数值.为表达方便,可列表如下:
由这一系列的对应值,可以得到一系列的有序实数对:
…,(-3,4.5),(-2,2),(-1,0.5),(0,0),(1,0.5),(2,2),(3,4.5),…
x … …
… …
y
-3
4.5
-2
2
-1
0.5
0.5
0
0
1
2
2
3
4.5
例1:画出函数y= x 的图象
1
—
2
2
●
●
●
●
●
●
●
x … -3 -2 -1 0 1 2 3 …
y … 4.5 2 0.5 0 0.5 2 4.5 …
画函数图象的步骤:一、列表
二、描点
三、连线
强调:1、描点画出的函数图象是局部的近似的,
要注意在所画出的曲线两端稍作延伸。
y= x
1
_
2
2
2、选点的个数及描点的准确、连线的光
滑都影响图象的准确度,画图时应用铅笔画图。
________________
__________
_______________________
画出简单函数的图象的步骤:
列表 (所取的数值必须符合函数自变量的取值范围)
描点 (借助虚线在平面中正确描出对应的点)
连线 (必须用光滑的曲线连接起来)
练 习:(课本P34练习)
在所给的直角坐标系中画出函数y=
x
的图象(先填写下表,再描点、连线).
-1.5
-1
-0.5
0
0.5
1
1.5
●
●
●
●
●
●
●
y= x
1
_
2
2、画出函数y=- 的图象
解:列表如下:
 ̄
6
x
x … -4 -3 -2 -1 … 1 2 3 4 …
y … 1.5 2 3 6 … -6 -3 -2 -1.5 …
y
-1
4
3
2
1
O
x
-2
-3
-4
-1
-2
1
2
3
4
.
5
.
.
.
.
.
.
连线:用光滑的曲线连线,就可得函数的图象了。
6
-3
-4
-5
-6
.
描点:
y=-
6
_
x
为什么没有“0”?
不同的函数具有不同的图象
y= x
1
_
2
2
y= x
1
_
2
y=-
6
_
x
回顾与小结
这节课你学到了什么?
思考:
点(-2,1)在y=- 的图象上吗?
若不在,那么(-2, )时,才会在y=- 上呢?
6
—
x
6
_
x
3
课后巩固:
1、阅读课本P32~34内容
2、完成课本P37习题18.2第4题(1)(2)
18.2.2 函数的图象
知识回顾
平面直角坐标系的建立过程:
(1)先画一条横轴,
再画一条纵轴。
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
(2) 找出点的位置
(-2,+3)(0,0)(2,4)
————
————
·
(-2,+3)
·
(0,0)
——————
————
·
(2,4)
·
·
A
B
(3)说出点A、B的坐标
(-3,-2)
(4,2)
第一象限
第二象限
第三象限
第四象限
______
____________
______
________________
下图是某日的气温变化图.
气温曲线上每一点(t,T)表示时间为t时的气温是T
点(10,2)
当t=10时,函数值T=2
点(14,5)
当t=14时,函数值T=5
______________
___
(10,2)
___________________
(14,5)
________
探究新知
问题:气温曲线是图象表示函数的一个实际例子。那么什么是函数图象呢?
一般来说,函数的图象是由直角坐标系中的一系列点组成,图象上的每一点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与它对应的函数值。
解:取自变量x的一些值,例如x=-3,-2,-1,0,1,2,3 …,计算出对应的函数值.为表达方便,可列表如下:
由这一系列的对应值,可以得到一系列的有序实数对:
…,(-3,4.5),(-2,2),(-1,0.5),(0,0),(1,0.5),(2,2),(3,4.5),…
x … …
… …
y
-3
4.5
-2
2
-1
0.5
0.5
0
0
1
2
2
3
4.5
例1:画出函数y= x 的图象
1
—
2
2
●
●
●
●
●
●
●
x … -3 -2 -1 0 1 2 3 …
y … 4.5 2 0.5 0 0.5 2 4.5 …
画函数图象的步骤:一、列表
二、描点
三、连线
强调:1、描点画出的函数图象是局部的近似的,
要注意在所画出的曲线两端稍作延伸。
y= x
1
_
2
2
2、选点的个数及描点的准确、连线的光
滑都影响图象的准确度,画图时应用铅笔画图。
________________
__________
_______________________
画出简单函数的图象的步骤:
列表 (所取的数值必须符合函数自变量的取值范围)
描点 (借助虚线在平面中正确描出对应的点)
连线 (必须用光滑的曲线连接起来)
练 习:(课本P34练习)
在所给的直角坐标系中画出函数y=
x
的图象(先填写下表,再描点、连线).
-1.5
-1
-0.5
0
0.5
1
1.5
●
●
●
●
●
●
●
y= x
1
_
2
2、画出函数y=- 的图象
解:列表如下:
 ̄
6
x
x … -4 -3 -2 -1 … 1 2 3 4 …
y … 1.5 2 3 6 … -6 -3 -2 -1.5 …
y
-1
4
3
2
1
O
x
-2
-3
-4
-1
-2
1
2
3
4
.
5
.
.
.
.
.
.
连线:用光滑的曲线连线,就可得函数的图象了。
6
-3
-4
-5
-6
.
描点:
y=-
6
_
x
为什么没有“0”?
不同的函数具有不同的图象
y= x
1
_
2
2
y= x
1
_
2
y=-
6
_
x
回顾与小结
这节课你学到了什么?
思考:
点(-2,1)在y=- 的图象上吗?
若不在,那么(-2, )时,才会在y=- 上呢?
6
—
x
6
_
x
3
课后巩固:
1、阅读课本P32~34内容
2、完成课本P37习题18.2第4题(1)(2)
