9.2.3 总体集中趋势的估计【新教材】人教A版(2019)高中数学必修第二册
文档属性
| 名称 | 9.2.3 总体集中趋势的估计【新教材】人教A版(2019)高中数学必修第二册 |  | |
| 格式 | zip | ||
| 文件大小 | 297.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-16 10:34:05 | ||
图片预览



文档简介
9.2.3 总体集中趋势的估计
课标解读
课标要求
核心素养
1.结合实例,能用样本估计总体的集中趋势参数(平均数、中位数、众数).(重点)
2.理解集中趋势参数的统计含义.(难点)
1.通过对平均数、中位数、众数概念的学习,培养学生数学抽象的核心素养.
2.通过利用样本的平均数、中位数、众数估计总体的平均数、中位数、众数,培养学生数据分析的核心素养.
王老板开了一家酒店,其中管理人员1人(王老板),亲戚6人,工作人员有5名领班,10名工人和1名学徒.现在需要增加一名新的工人.王老板打出的招聘宣传语是“本酒店待遇丰厚,平均工资是每周300元”.小强看了后赶来应聘.工作了一段时间后,小强去找王老板:“你骗了我.我问过其他工人了,没有一个工人每周的工资超过200元,你当时怎么宣传工资一周是300元呢?”而王老板说:“我当时说的是平均工资300元,不信,你看工资表.”工资表如下(单位:元):
人员
老板
亲戚
领班
工人
学徒
合计
工资
2
220
250
220
200
100
—
人数
1
6
5
10
1
23
合计
2
220
1
500
1
100
2
000
100
6
920
问题:你认为王老板的说法合理吗?
1.众数、中位数和平均数的定义
(1)众数:一组数据中①出现次数最多的数.
(2)中位数:一组数据按大小顺序排列后,处于②中间位置的数.如果这组数据是偶数个,则取③中间两个数据的平均数.
(3)平均数:一组数据的④和除以数据个数所得到的数.
2.众数、中位数、平均数与频率分布直方图的关系
(1)平均数:在频率分布直方图中,样本平均数可以用每个小矩形底边中点的⑤横坐标与小矩形的⑥面积的乘积之和近似代替.
(2)中位数:在频率分布直方图中,中位数左边和右边的直方图的面积应该⑦相等.
(3)众数:众数是⑧最高小矩形底边的中点所对应的数据.
特别提醒
众数、中位数和平均数的比较
名称
优点
缺点
平均数
与中位数相比,平均数反映出样本数据中更多的信息,对样本中的极端值更加敏感
任何一个数据的改变都会引起平均数的改变.数据越“离群”,对平均数的影响越大
中位数
不受少数几个极端数据(即排序靠前或靠后的数据)的影响
对极端值不敏感
众数
体现了样本数据的最大集中点
众数只能传递数据中信息很少的一部分,对极端值不敏感
思考1:中位数一定是样本数据中的一个数吗?
思考2:一组数据的众数可以有几个?中位数是否也具有相同的结论?
探究一 中位数、众数、平均数的计算
例1 在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示:
成绩(单位:m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这17名运动员成绩的众数、中位数与平均数.
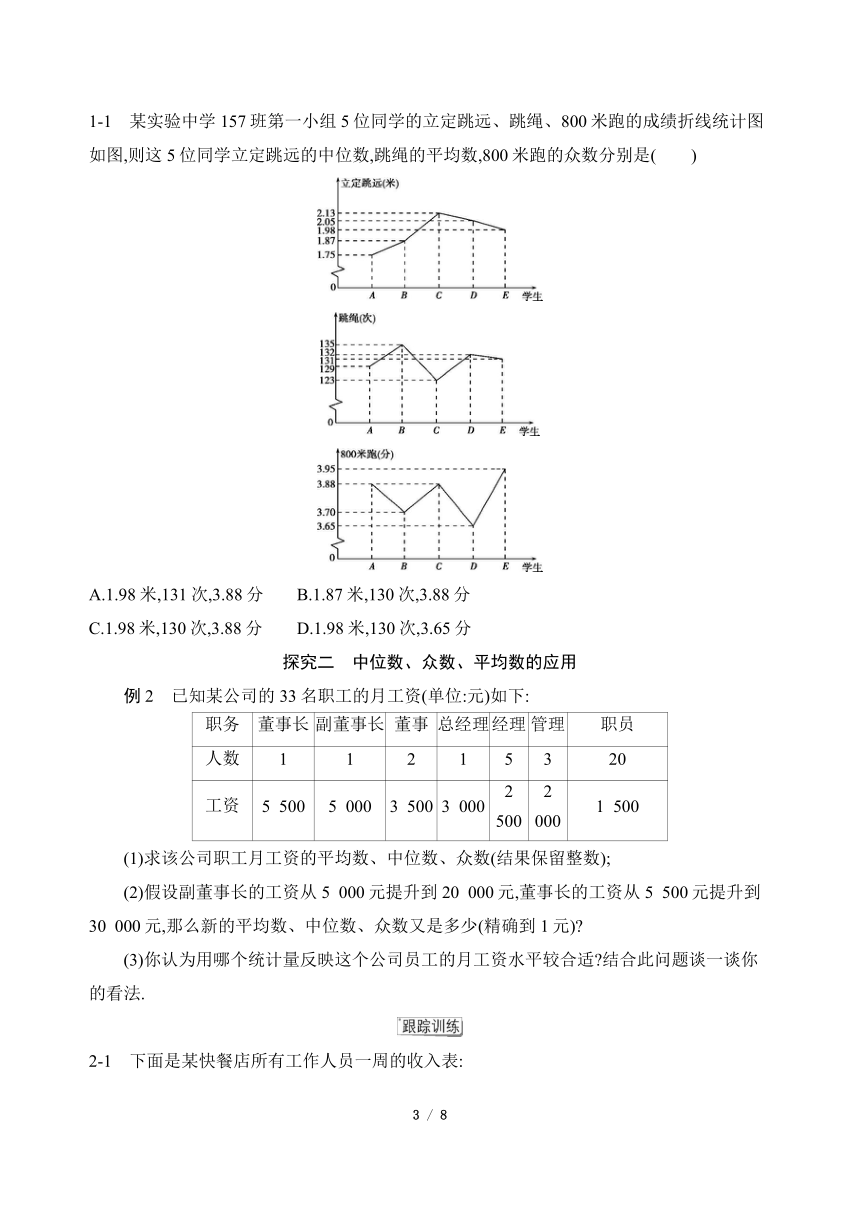
1-1 某实验中学157班第一小组5位同学的立定跳远、跳绳、800米跑的成绩折线统计图如图,则这5位同学立定跳远的中位数,跳绳的平均数,800米跑的众数分别是( )
A.1.98米,131次,3.88分
B.1.87米,130次,3.88分
C.1.98米,130次,3.88分
D.1.98米,130次,3.65分
探究二 中位数、众数、平均数的应用
例2 已知某公司的33名职工的月工资(单位:元)如下:
职务
董事长
副董事长
董事
总经理
经理
管理
职员
人数
1
1
2
1
5
3
20
工资
5
500
5
000
3
500
3
000
2
500
2
000
1
500
(1)求该公司职工月工资的平均数、中位数、众数(结果保留整数);
(2)假设副董事长的工资从5
000元提升到20
000元,董事长的工资从5
500元提升到30
000元,那么新的平均数、中位数、众数又是多少(精确到1元)?
(3)你认为用哪个统计量反映这个公司员工的月工资水平较合适?结合此问题谈一谈你的看法.
2-1 下面是某快餐店所有工作人员一周的收入表:
老板
大厨
二厨
采购员
杂工
服务生
会计
3
000元
450元
350元
400元
320元
320元
410元
(1)计算所有人员的周平均收入;
(2)(1)中求得的周平均收入能反映打工人员的周收入的一般水平吗?为什么?
(3)去掉老板的收入后,再计算平均收入,这能代表打工人员的周收入的水平吗?
探究三 根据频率分布直方图求平均数、中位数和众数
例3 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(1)求这次测试数学成绩的众数;
(2)求这次测试数学成绩的中位数.
1.(变问法)若例3的条件不变,求数学成绩的平均分.
2.(变问法)若例3条件不变,求80分以下的学生人数.
1.新莽铜嘉量是由王莽国师刘歆等人设计制造的标准量器,它包括了龠(yuè)、合、升、斗、斛这五个容量单位.每一个量又有详细的分铭,记录了各器的径、深、底面积和容积.根据铭文不但可以直接测得各个容量单位的量值,而且可以通过对径、深各个部位的测量,得到精确的计算容积,从而推算出当时的标准尺度.现根据铭文计算,当时制造容器时所用的圆周率分别为3.154
7,3.199
2,3.149
8,3.203
1,比径一周三的古率已有所进步,则上面四个数与祖冲之给出的约率、密率,这6个数据的中位数为( )
A.3.142
9
B.3.152
3
C.3.149
8
D.3.154
7
2.一组样本数据为19,23,12,14,14,17,10,12,18,14,27,则这组数据的众数和中位数分别为( )
A.14,14
B.12,14
C.14,15.5
D.12,15.5
3.某高校有甲、乙两个数学建模兴趣班.其中甲班有40人,乙班有50人.现分析两个班的一次考试成绩,得到甲班的平均成绩是90分,乙班的平均成绩是81分,则该校数学建模兴趣班的平均成绩是 分.?
4.某中学举行电脑知识竞赛,现将高一参赛学生的成绩(单位:分)进行整理后分成五组,绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.求:
(1)高一参赛学生成绩的众数、中位数;
(2)高一参赛学生的平均成绩.
1.七位评委为某跳水运动员打出的分数如下:
84,79,86,87,84,93,84,则这组分数的中位数和众数分别是( )
A.84,85
B.84,84
C.85,84
D.85,85
2.一组观察值4,3,5,6出现的次数分别为3,2,4,2,则样本平均值约为( )
A.4.55
B.4.5
C.12.5
D.1.64
3.某工厂对一批新产品的长度(单位:mm)进行检测,下图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
A.20
B.25
C.22.5
D.22.75
4.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为a,而x4,x5,x6,…,x10的平均数为b,则样本数据的平均数为( )
A.
B.
C.
D.
5.在某次考试中,共有100名学生参加考试,如果某题的得分情况如下表:
得分
0分
1分
2分
3分
4分
百分率
37.0%
8.6%
6.0%
28.2%
20.2%
那么这些得分的众数是( )
A.37.0%
B.20.2%
C.0分
D.4分
6.一组数据2,x,4,6,10的平均数是5,则x= .?
7.已知一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,则这组数据的平均数为 .?
8.某学校为了了解学生课外阅读情况,随机调查了50名学生,得到他们在每一天各自课外阅读所用时间的数据,结果用条形统计图表示如下,根据条形统计图估计该校全体学生这一天平均每人的课外阅读时间为 h.?
9.为了调查某厂工人生产某种产品的能力,随机抽查了20名工人某天生产该产品的数量,得到如下频率分布直方图.
求:(1)这20名工人中一天生产该产品的数量在[55,75)的人数;
(2)这20名工人中一天生产该产品的数量的中位数;
(3)这20名工人中一天生产该产品的数量的平均数.
10.(多选题)在某次高中学科竞赛中,4
000名考生的参赛成绩统计图如图所示,60分以下视为不及格,若同一组中的数据用该组区间中点值为代表,则下列说法中正确的是( )
A.成绩在[70,80)分的考生人数最多
B.不及格的考生人数为1
000
C.考生竞赛成绩的平均分约为70.5分
D.考生竞赛成绩的中位数为75分
11.某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)如下所示:
甲的成绩是75,83,85,85,92.
乙的成绩是74,84,84,85,98.
甲、乙两位同学得分的中位数分别为x1,x2,得分的平均数分别为y1,y2,则下列结论正确的是( )
A.x1B.x1y2
C.x1>x2,y1>y2
D.x1>x2,y112.某工厂人员及月工资如下表:
人员
经理
管理
人员
高级
技工
工人
学徒
合计
月工资
(元)
22
000
2
500
2
200
2
000
1
000
29
700
人数
1
6
5
10
1
23
合计
22
000
15
000
11
000
20
000
1
000
69
000
(1)指出这个表格中月工资的众数、中位数和平均数;
(2)这个表格中,平均数能客观地反映该工厂的月工资水平吗?为什么?
14
/
15
课标解读
课标要求
核心素养
1.结合实例,能用样本估计总体的集中趋势参数(平均数、中位数、众数).(重点)
2.理解集中趋势参数的统计含义.(难点)
1.通过对平均数、中位数、众数概念的学习,培养学生数学抽象的核心素养.
2.通过利用样本的平均数、中位数、众数估计总体的平均数、中位数、众数,培养学生数据分析的核心素养.
王老板开了一家酒店,其中管理人员1人(王老板),亲戚6人,工作人员有5名领班,10名工人和1名学徒.现在需要增加一名新的工人.王老板打出的招聘宣传语是“本酒店待遇丰厚,平均工资是每周300元”.小强看了后赶来应聘.工作了一段时间后,小强去找王老板:“你骗了我.我问过其他工人了,没有一个工人每周的工资超过200元,你当时怎么宣传工资一周是300元呢?”而王老板说:“我当时说的是平均工资300元,不信,你看工资表.”工资表如下(单位:元):
人员
老板
亲戚
领班
工人
学徒
合计
工资
2
220
250
220
200
100
—
人数
1
6
5
10
1
23
合计
2
220
1
500
1
100
2
000
100
6
920
问题:你认为王老板的说法合理吗?
1.众数、中位数和平均数的定义
(1)众数:一组数据中①出现次数最多的数.
(2)中位数:一组数据按大小顺序排列后,处于②中间位置的数.如果这组数据是偶数个,则取③中间两个数据的平均数.
(3)平均数:一组数据的④和除以数据个数所得到的数.
2.众数、中位数、平均数与频率分布直方图的关系
(1)平均数:在频率分布直方图中,样本平均数可以用每个小矩形底边中点的⑤横坐标与小矩形的⑥面积的乘积之和近似代替.
(2)中位数:在频率分布直方图中,中位数左边和右边的直方图的面积应该⑦相等.
(3)众数:众数是⑧最高小矩形底边的中点所对应的数据.
特别提醒
众数、中位数和平均数的比较
名称
优点
缺点
平均数
与中位数相比,平均数反映出样本数据中更多的信息,对样本中的极端值更加敏感
任何一个数据的改变都会引起平均数的改变.数据越“离群”,对平均数的影响越大
中位数
不受少数几个极端数据(即排序靠前或靠后的数据)的影响
对极端值不敏感
众数
体现了样本数据的最大集中点
众数只能传递数据中信息很少的一部分,对极端值不敏感
思考1:中位数一定是样本数据中的一个数吗?
思考2:一组数据的众数可以有几个?中位数是否也具有相同的结论?
探究一 中位数、众数、平均数的计算
例1 在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示:
成绩(单位:m)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这17名运动员成绩的众数、中位数与平均数.
1-1 某实验中学157班第一小组5位同学的立定跳远、跳绳、800米跑的成绩折线统计图如图,则这5位同学立定跳远的中位数,跳绳的平均数,800米跑的众数分别是( )
A.1.98米,131次,3.88分
B.1.87米,130次,3.88分
C.1.98米,130次,3.88分
D.1.98米,130次,3.65分
探究二 中位数、众数、平均数的应用
例2 已知某公司的33名职工的月工资(单位:元)如下:
职务
董事长
副董事长
董事
总经理
经理
管理
职员
人数
1
1
2
1
5
3
20
工资
5
500
5
000
3
500
3
000
2
500
2
000
1
500
(1)求该公司职工月工资的平均数、中位数、众数(结果保留整数);
(2)假设副董事长的工资从5
000元提升到20
000元,董事长的工资从5
500元提升到30
000元,那么新的平均数、中位数、众数又是多少(精确到1元)?
(3)你认为用哪个统计量反映这个公司员工的月工资水平较合适?结合此问题谈一谈你的看法.
2-1 下面是某快餐店所有工作人员一周的收入表:
老板
大厨
二厨
采购员
杂工
服务生
会计
3
000元
450元
350元
400元
320元
320元
410元
(1)计算所有人员的周平均收入;
(2)(1)中求得的周平均收入能反映打工人员的周收入的一般水平吗?为什么?
(3)去掉老板的收入后,再计算平均收入,这能代表打工人员的周收入的水平吗?
探究三 根据频率分布直方图求平均数、中位数和众数
例3 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(1)求这次测试数学成绩的众数;
(2)求这次测试数学成绩的中位数.
1.(变问法)若例3的条件不变,求数学成绩的平均分.
2.(变问法)若例3条件不变,求80分以下的学生人数.
1.新莽铜嘉量是由王莽国师刘歆等人设计制造的标准量器,它包括了龠(yuè)、合、升、斗、斛这五个容量单位.每一个量又有详细的分铭,记录了各器的径、深、底面积和容积.根据铭文不但可以直接测得各个容量单位的量值,而且可以通过对径、深各个部位的测量,得到精确的计算容积,从而推算出当时的标准尺度.现根据铭文计算,当时制造容器时所用的圆周率分别为3.154
7,3.199
2,3.149
8,3.203
1,比径一周三的古率已有所进步,则上面四个数与祖冲之给出的约率、密率,这6个数据的中位数为( )
A.3.142
9
B.3.152
3
C.3.149
8
D.3.154
7
2.一组样本数据为19,23,12,14,14,17,10,12,18,14,27,则这组数据的众数和中位数分别为( )
A.14,14
B.12,14
C.14,15.5
D.12,15.5
3.某高校有甲、乙两个数学建模兴趣班.其中甲班有40人,乙班有50人.现分析两个班的一次考试成绩,得到甲班的平均成绩是90分,乙班的平均成绩是81分,则该校数学建模兴趣班的平均成绩是 分.?
4.某中学举行电脑知识竞赛,现将高一参赛学生的成绩(单位:分)进行整理后分成五组,绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.求:
(1)高一参赛学生成绩的众数、中位数;
(2)高一参赛学生的平均成绩.
1.七位评委为某跳水运动员打出的分数如下:
84,79,86,87,84,93,84,则这组分数的中位数和众数分别是( )
A.84,85
B.84,84
C.85,84
D.85,85
2.一组观察值4,3,5,6出现的次数分别为3,2,4,2,则样本平均值约为( )
A.4.55
B.4.5
C.12.5
D.1.64
3.某工厂对一批新产品的长度(单位:mm)进行检测,下图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
A.20
B.25
C.22.5
D.22.75
4.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为a,而x4,x5,x6,…,x10的平均数为b,则样本数据的平均数为( )
A.
B.
C.
D.
5.在某次考试中,共有100名学生参加考试,如果某题的得分情况如下表:
得分
0分
1分
2分
3分
4分
百分率
37.0%
8.6%
6.0%
28.2%
20.2%
那么这些得分的众数是( )
A.37.0%
B.20.2%
C.0分
D.4分
6.一组数据2,x,4,6,10的平均数是5,则x= .?
7.已知一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,则这组数据的平均数为 .?
8.某学校为了了解学生课外阅读情况,随机调查了50名学生,得到他们在每一天各自课外阅读所用时间的数据,结果用条形统计图表示如下,根据条形统计图估计该校全体学生这一天平均每人的课外阅读时间为 h.?
9.为了调查某厂工人生产某种产品的能力,随机抽查了20名工人某天生产该产品的数量,得到如下频率分布直方图.
求:(1)这20名工人中一天生产该产品的数量在[55,75)的人数;
(2)这20名工人中一天生产该产品的数量的中位数;
(3)这20名工人中一天生产该产品的数量的平均数.
10.(多选题)在某次高中学科竞赛中,4
000名考生的参赛成绩统计图如图所示,60分以下视为不及格,若同一组中的数据用该组区间中点值为代表,则下列说法中正确的是( )
A.成绩在[70,80)分的考生人数最多
B.不及格的考生人数为1
000
C.考生竞赛成绩的平均分约为70.5分
D.考生竞赛成绩的中位数为75分
11.某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)如下所示:
甲的成绩是75,83,85,85,92.
乙的成绩是74,84,84,85,98.
甲、乙两位同学得分的中位数分别为x1,x2,得分的平均数分别为y1,y2,则下列结论正确的是( )
A.x1
C.x1>x2,y1>y2
D.x1>x2,y1
人员
经理
管理
人员
高级
技工
工人
学徒
合计
月工资
(元)
22
000
2
500
2
200
2
000
1
000
29
700
人数
1
6
5
10
1
23
合计
22
000
15
000
11
000
20
000
1
000
69
000
(1)指出这个表格中月工资的众数、中位数和平均数;
(2)这个表格中,平均数能客观地反映该工厂的月工资水平吗?为什么?
14
/
15
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
