七年级数学8.2.2用加减消元法解二元一次方程组
文档属性
| 名称 | 七年级数学8.2.2用加减消元法解二元一次方程组 |

|
|
| 格式 | zip | ||
| 文件大小 | 143.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-23 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
8.2.2 加减消元法
解二元一次方程组
授课教师:付美玲
七(5)班
学习目标:
掌握用加减消元法来解二元一次方程组
学习重点:
探寻用加减消元法解二元一次方程组的过程
学习难点:
消元的转化过程
一变,二代,三消,四解,五再代,六总结
选取方程,适当变形,用含一个未知数的式子去表示另一个未知数。
变形后的方程代入另一个方程,得到一元一次方程。
解这个一元一次方程,得未知数的值。
将所得的值,代入变形方程,求得另一个未知数的值,得方程组的解。
检验所得结果是否正确。
写出方程组的解
用代入法解方程组的步骤
2.用代入法解这个方程组
①
②
将③代入②中得,
解这个方程,得
把 代入③中,得
2.用代入法解这个方程组
①
②
2.用代入法解这个方程组
①
②
①
2.用代入法解这个方程组
②
①
所以这个方程组的解是
所以这个方程组的解是
í
ì
y=
x=
解:由①得
③
解:由①得
想一想 :这个方程组 如果不用代入消元法还可不可以解得呢?
认真观察:
方程组的系数有什么特殊的地方吗?
y 的系数互为相反数
由此可以得出将这两个方程左右两边分别相加起来就能把y消去
①
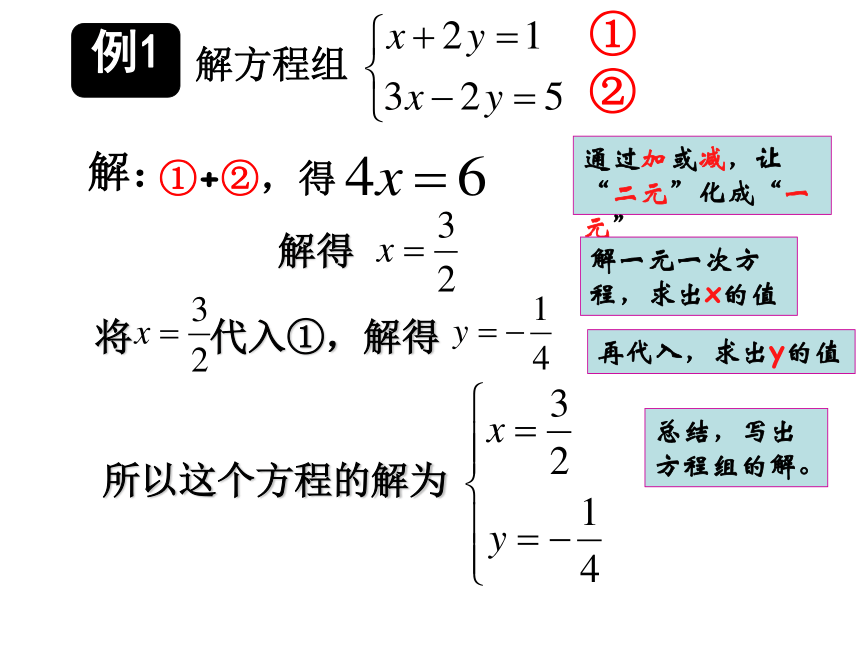
例1
解方程组
②
解:
①+②,得
通过加或减,让“二元”化成“一元”
解一元一次方程,求出x的值
解得
再代入,求出y的值
将 代入①,解得
总结,写出方程组的解。
所以这个方程的解为
加减消元法的定义:
两个二元一次方程中同一未知数的系数相反或者相等时,把这两个方程的两边分别相加或者相减,消去一个未知数,把解二元一次方程组转化为解一元一次方程。这种解方程组的方法称为加减消元法,简称为加减法。
加减消元法解方程组的基本思想是: 消元。
1.利用加减消元法解方程组时在所有的方程组的两个方程中,某个未知数的系数互为相反数,则可以直接 消去这个未知数;
如果某个未知数系数相等,则可以直接 消去这个未知数。
一.填空题:
把这两个方程中的两边分别相加
把这两个方程中的两边分别相减
分别相加
y
2.已知方程组
x+3y=17
2x-3y=6
两个方程只要两边
就可以消去未知数
分别相减
3.已知方程组
25x-7y=16
25x+6y=10
两个方程只要两边
就可以消去未知数
x
二.选择题
1. 用加减法解方程组
6x+7y=-19①
6x-5y=17②
应用( )
A.①-②消去y
B.①-②消去x
C. ②- ①消去常数项
D. 以上都不对
B
2.方程组
3x+2y=13
3x-2y=5
消去y后所得的方程是( )
B
A.6x=8
B.6x=18
C.6x=5
D.x=18
用加减消元法解方程组
(1)
(2)
(3)
í
ì
=
-
=
+
8
32
x
2y
6y
x
í
ì
-
=
+
-
=
-
26
4
5
2
2
5
y
x
y
x
í
ì
y=5
x= 2
í
ì
y=-4
x=-2
í
ì
y=18
x=9
(1)
(2)
(3)
í
ì
=
-
=
+
0
2
36
2
y
x
y
x
解方程组
例2
5x-2y= 4
2x-3y= -5
系数不相等也不互为相反数怎么办?
想办法变形把系数变成相等或者互为相反数!!!
解:①×3,得 15x-6y= 12 ③
②×2,得 4x-6y= -10 ④
③-④ 得 11x=22
x=2
①
②
将x=2代入①中,得
y=3
所以这个方程组的解是
í
ì
y=3
x=2
1.先确定消去哪一个未知数;
2.再找出相应系数的最小公倍数;
3.确定每一个方程两边应同乘以几.
当方程组中没有同一个未知数的系数相反或相同的时候可以按以下步骤做:
1.解下列方程组
(1)
(2)
(3)
本课小结:
加减消元法解二元一次方程组的注意事项:
1.同一个未知数的系数相反或者相同的时候直接相加或者相减;
2.没有同一个未知数相反或者相同的时候需要找最小公倍数变形使得系数相反或者相同,再进行相加减(要注意变形的时候方程的每一项都要乘以最小公倍数)。
3.加减消元法的步骤:
一变形,二加减 , 三代入, 四求解 ,五再代 ,六总结
作业
课本 P-102 练习题 1
课本 P-103 习题3
8.2.2 加减消元法
解二元一次方程组
授课教师:付美玲
七(5)班
学习目标:
掌握用加减消元法来解二元一次方程组
学习重点:
探寻用加减消元法解二元一次方程组的过程
学习难点:
消元的转化过程
一变,二代,三消,四解,五再代,六总结
选取方程,适当变形,用含一个未知数的式子去表示另一个未知数。
变形后的方程代入另一个方程,得到一元一次方程。
解这个一元一次方程,得未知数的值。
将所得的值,代入变形方程,求得另一个未知数的值,得方程组的解。
检验所得结果是否正确。
写出方程组的解
用代入法解方程组的步骤
2.用代入法解这个方程组
①
②
将③代入②中得,
解这个方程,得
把 代入③中,得
2.用代入法解这个方程组
①
②
2.用代入法解这个方程组
①
②
①
2.用代入法解这个方程组
②
①
所以这个方程组的解是
所以这个方程组的解是
í
ì
y=
x=
解:由①得
③
解:由①得
想一想 :这个方程组 如果不用代入消元法还可不可以解得呢?
认真观察:
方程组的系数有什么特殊的地方吗?
y 的系数互为相反数
由此可以得出将这两个方程左右两边分别相加起来就能把y消去
①
例1
解方程组
②
解:
①+②,得
通过加或减,让“二元”化成“一元”
解一元一次方程,求出x的值
解得
再代入,求出y的值
将 代入①,解得
总结,写出方程组的解。
所以这个方程的解为
加减消元法的定义:
两个二元一次方程中同一未知数的系数相反或者相等时,把这两个方程的两边分别相加或者相减,消去一个未知数,把解二元一次方程组转化为解一元一次方程。这种解方程组的方法称为加减消元法,简称为加减法。
加减消元法解方程组的基本思想是: 消元。
1.利用加减消元法解方程组时在所有的方程组的两个方程中,某个未知数的系数互为相反数,则可以直接 消去这个未知数;
如果某个未知数系数相等,则可以直接 消去这个未知数。
一.填空题:
把这两个方程中的两边分别相加
把这两个方程中的两边分别相减
分别相加
y
2.已知方程组
x+3y=17
2x-3y=6
两个方程只要两边
就可以消去未知数
分别相减
3.已知方程组
25x-7y=16
25x+6y=10
两个方程只要两边
就可以消去未知数
x
二.选择题
1. 用加减法解方程组
6x+7y=-19①
6x-5y=17②
应用( )
A.①-②消去y
B.①-②消去x
C. ②- ①消去常数项
D. 以上都不对
B
2.方程组
3x+2y=13
3x-2y=5
消去y后所得的方程是( )
B
A.6x=8
B.6x=18
C.6x=5
D.x=18
用加减消元法解方程组
(1)
(2)
(3)
í
ì
=
-
=
+
8
32
x
2y
6y
x
í
ì
-
=
+
-
=
-
26
4
5
2
2
5
y
x
y
x
í
ì
y=5
x= 2
í
ì
y=-4
x=-2
í
ì
y=18
x=9
(1)
(2)
(3)
í
ì
=
-
=
+
0
2
36
2
y
x
y
x
解方程组
例2
5x-2y= 4
2x-3y= -5
系数不相等也不互为相反数怎么办?
想办法变形把系数变成相等或者互为相反数!!!
解:①×3,得 15x-6y= 12 ③
②×2,得 4x-6y= -10 ④
③-④ 得 11x=22
x=2
①
②
将x=2代入①中,得
y=3
所以这个方程组的解是
í
ì
y=3
x=2
1.先确定消去哪一个未知数;
2.再找出相应系数的最小公倍数;
3.确定每一个方程两边应同乘以几.
当方程组中没有同一个未知数的系数相反或相同的时候可以按以下步骤做:
1.解下列方程组
(1)
(2)
(3)
本课小结:
加减消元法解二元一次方程组的注意事项:
1.同一个未知数的系数相反或者相同的时候直接相加或者相减;
2.没有同一个未知数相反或者相同的时候需要找最小公倍数变形使得系数相反或者相同,再进行相加减(要注意变形的时候方程的每一项都要乘以最小公倍数)。
3.加减消元法的步骤:
一变形,二加减 , 三代入, 四求解 ,五再代 ,六总结
作业
课本 P-102 练习题 1
课本 P-103 习题3
